Гипергеометрическое распределение вероятностей

Распределение и формула Пуассона

В данной статье мы рассмотрим ещё одно дискретное распределение, которое получило широкое распространение на практике. Не успел я открыть курс по теории вероятностей, как сразу стали поступать запросы: «Где Пуассон? Где задачи на формулу Пуассона?» и т.п. И поэтому я начну с частного применения распределения Пуассона – ввиду большой востребованности материала.

Задача до ~~боли~~ эйфории знакома:

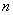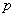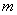– проводится независимых испытаний, в каждом из которых случайное событие может появиться с вероятностью . Требуется найти вероятность того, что в данной серии испытаний событие появится ровно раз.

Наверное, вам уже снится формула Бернулли:)

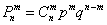
тем более, на уроке о биномиальном распределении вероятностей мы разобрали ситуацию по косточкам.

В том случае, если количество испытаний 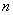велико (сотни и тысячи), эту вероятность обычно рассчитывают приближённо – с помощью локальной теоремы Лапласа: , где .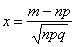

Однако и тут есть «слабое звено» – теорема Лапласа начинает серьёзно барахлить (давать большую погрешность), если вероятность 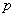меньше, чем 0,1 (и чем меньше, тем всё хуже). Поэтому здесь используют другой метод, и именно распределение Пуассона.

Итак, если количество испытаний 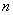достаточно велико, а вероятность 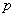появления события в отдельно взятом испытании весьма мала (0,05-0,1 и меньше), то вероятность того, что в данной серии испытаний событие появится ровно 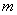раз, можно приближенно вычислить по формуле Пуассона:
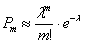, где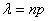

Напоминаю, что ноль факториал 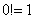, а значит, формула имеет смысл и для .

Вместо «лямбды» также используют букву «а».

Пример 1

В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,0002. Найти вероятность того, что за месяц откажет ровно 1 замок.

Утопичная, конечно, задача, но что делать – решаем:)

В данном случае количество «испытаний» 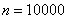велико, а вероятность «успеха» в каждом из них – мала: , поэтому используем формулу Пуассона:

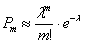
Вычислим:
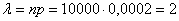– по существу, это среднеожидаемое количество вышедших из строя замков.

Таким образом:
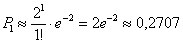– вероятность того, что за месяц из строя выйдет ровно 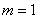один замок (из 10 тысяч).

Ответ: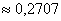

С технической точки зрения этот результат можно получить несколькими способами, расскажу о них в историческом ракурсе:

1) С помощью специальной таблицы, которая до сих пор встречается во многих книгах по терверу. В данную таблицу сведены различные значения 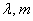и соответствующие им вероятности. Табулирование обусловлено тем, что в своё время не существовало бытовых калькуляторов, на которых можно было бы подсчитать значения экспоненциальной функции. Отсюда, кстати, идёт традиция округлять вычисления до 4 знаков после запятой – как в стандартной таблице.

2) С помощью прямого вычисления на микрокалькуляторе (прогресс!).

3) С помощью стандартной экселевской функции:
=ПУАССОН(m; лямбда; 0)
в данной задаче вбиваем в любую ячейку Экселя =ПУАССОН(1; 2; 0) и жмём Enter.

Следует отметить, что развитие вычислительной техники фактически отправило в историю методы Лапласа, да и рассматриваемый метод тоже – по той причине, что ответ легко вычислить более точно по формуле Бернулли:

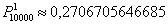
Здесь я использовал функцию БИНОМРАСП, о которой неоднократно упоминал ранее.

Но формула Пуассона, тем не менее, даёт очень крутое приближение:
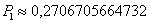– с погрешностью только на 9 знаке после запятой!

Впрочем, это всё лирика, решать-то всё равно нужно по формуле Пуассона:

Пример 2

Завод отправил в торговую сеть 500 изделий. Вероятность повреждения изделия в пути равна 0,003. Найти вероятность того, что при транспортировке будет повреждено: а) ни одного изделия, б) ровно три изделия, в) более трех изделий.

Классика жанра.

Решение: используем формулу Пуассона:

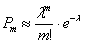
В данном случае:
– среднеожидаемое количество повреждённых изделий

а)
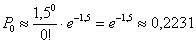– вероятность того, что все изделия дойдут в целости и сохранности. Ничего не украдут, одним словом :)

б)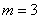
– вероятность того, что в пути будут повреждены ровно 3 изделия из 500.

в)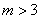
А тут всё немножко хитрее. Сначала найдём 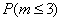– вероятность того, что в пути повредятся не более трёх изделий. По теореме сложения вероятностей несовместных событий:

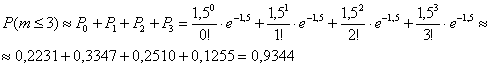
Само собой, ручками это считать надоест, и поэтому я добавил в свой расчётный макет автоматическое построение распределения Пуассона (см. Пункт 7) – пользуйтесь на здоровье.

По теореме сложения вероятностей противоположных событий:
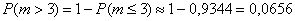– вероятность того, что при доставке будет повреждено более 3 изделий.

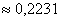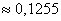Ответ: а) , б) , в)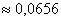

Самостоятельно:

Пример 3

Вероятность изготовления бракованных деталей при их массовом производстве равна 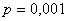. Определить вероятность того, что в партии из 800 деталей будет: а) ровно 2 бракованные, б) не более двух.

Решение и ответ в конце урока.

Встречаются и другие формулировки условия. Так, в предложенной задаче может идти речь о том, что производственный брак составляет 0,1% или «в среднем 1 деталь на каждую тысячу». Бывает и дано готовое значение «лямбда», например: «В стандартной партии из 800 деталей брак в среднем составляет 0,8 деталей. Найти вероятность того, что в очередной партии…».

В этой связи ни в коем случае не отключаем голову – даже в таких простых примерах!

А теперь о самом распределении Пуассона. Случайная величина , распределённая по этому закону, принимает бесконечное и счётное количество значений 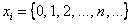, вероятности появления которых определяются формулой:

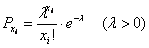
Или, если расписать подробно:

Вспоминая разложение экспоненты в ряд, легко убедиться, что:

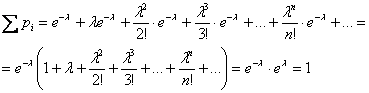
В теории установлено, что математическое ожидание пуассоновской случайной величины равно 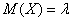и дисперсия – тому же самому значению: .

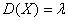Обратите внимание, что во всех вышеприведённых заданиях мы лишь ПОЛЬЗОВАЛИСЬ распределением Пуассона для приближенного расчёта вероятностей, в то время как ТОЧНЫЕ значения следовало находить по формуле Бернулли, т.е., там имело место биномиальное распределение.

И следующие две задачи принципиально отличаются от предыдущих:

Пример 4

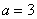Случайная величина подчинена закону Пуассона с математическим ожиданием . Найти вероятность того, что данная случайная величина примет значение, меньшее, чем ее математическое ожидание.

Отличие состоит в том, что здесь речь идёт ИМЕННО о распределении Пуассона.

Решение: случайная величина принимает значения 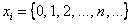с вероятностями:

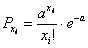
По условию, 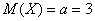, и тут всё просто: событие 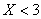состоит в трёх несовместных исходах:

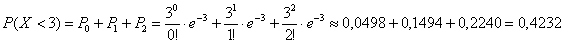вероятность того, что случайная величина примет значение, меньшее, чем ее математическое ожидание.

Ответ:

Аналогичная задача на понимание:

Пример 5

Случайная величина подчинена закону Пуассона с математическим ожиданием 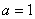. Найти вероятность того, что данная случайная величина примет положительное значение.

Решение и ответ в конце урока.

Помимо приближения биномиального распределения (Примеры 1-3), распределение Пуассона нашло широкое применение в теории массового обслуживания для вероятностной характеристики простейшего потока событий. Постараюсь быть лаконичным:

Пусть в некоторую систему поступают заявки (телефонные звонки, приходящие клиенты и т.д.). Поток заявок называют простейшим, если он удовлетворяет условиям стационарности, отсутствия последствий и ординарности. Стационарность подразумевает то, что интенсивность заявок постоянна и не зависит от времени суток, дня недели или других временнЫх рамок. Иными словами, не бывает «часа пик» и не бывает «мёртвых часов». Отсутствие последствий означает, что вероятность появления новых заявок не зависит от «предыстории», т.е. нет такого, что «одна бабка рассказала» и другие «набежали» (или наоборот, разбежались). И, наконец, свойство ординарности характеризуется тем, что за достаточно малый промежуток времени практически невозможно появление двух или бОльшего количества заявок. «Две старушки в дверь?» – нет уж, увольте~~, рубить удобнее по порядку~~.

Итак, пусть в некоторую систему поступает простейший поток заявок со средней интенсивностью заявок в некоторую единицу времени (минуту, час, день или в любую другую). Тогда вероятность того, что за данный промежуток времени, в систему поступит ровно 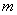заявок, равна:

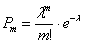
Пример 6

Звонки в диспетчерскую такси представляет собой простейший пуассоновский поток со средней интенсивностью 30 вызовов в час. Найти вероятность того, что: а) за 1 мин. поступит 2-3 вызова, б) в течение пяти минут будет хотя бы один звонок.

Решение: используем формулу Пуассона:

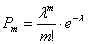
а) Учитывая стационарность потока, вычислим среднее количество вызовов за 1 минуту:
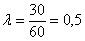вызова – в среднем за одну минуту.

По теореме сложения вероятностей несовместных событий:
– вероятность того, что за 1 минуту в диспетчерскую поступит 2-3 вызова.

б) Вычислим среднее количество вызов за пять минут:

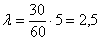
По формуле Пуассона:
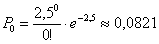– вероятность того, что в течение 5 минут не будет ни одного звонка.

По теореме сложения вероятностей противоположных событий:
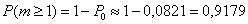– вероятность того, что в течение 5 минут будет хотя бы один вызов.

Ответ: а) , б)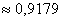

Заметьте, что, несмотря на конечное количество возможных звонков (а оно в принципе конечно), здесь имеет место именно распределение Пуассона, а не какое-то другое

Для самостоятельного решения:

Пример 7

Среднее число автомобилей, проходящих таможенный досмотр в течение часа, равно 3. Найти вероятность того, что: а) за 2 часа пройдут досмотр от 7 до 10 автомобилей; б) за пол часа успеет пройти досмотр только 1 автомобиль.

Решение и ответ в конце урока.

Наверное, многие знают, что теория массового обслуживания – это обширный и очень интересный раздел прикладной математики, и сейчас мы познакомились с простейшей его задачей.

Дополнительные примеры на распределение и формулу Пуассона можно найти в тематической pdf-книге, и я предлагаю вам ознакомиться с ещё одной популярной вещью – Гипергеометрическим распределением вероятностей.

Приятного и полезного чтения!

Решения и ответы:

Пример 3. Решение:используем формулу Пуассона:
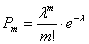, в данном случае:

а) – вероятность того, что в данной партии окажется ровно 2 бракованные детали.
б) По теореме сложения вероятностей несовместных событий:

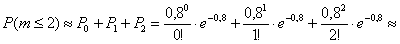
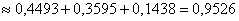– вероятность того, что в данной партии окажется не более 2 бракованных изделий.

Ответ: а) 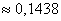, б)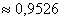

Пример 5. Решение: случайная величина принимает значения 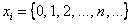с вероятностями 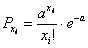. По условию, .
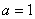Найдём вероятность того, что случайная величина примет нулевое значение:

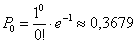
По теореме сложения вероятностей противоположных событий:
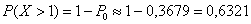– вероятность того, что случайная величина примет положительное значение

Ответ: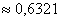

Пример 7. Решение: предполагая поток простым, используем формулу Пуассона:

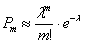
а) Вычислим 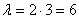– среднее количество автомобилей, проходящих таможенный досмотр, в течение 2 часов.
По теореме сложения вероятностей несовместных событий:

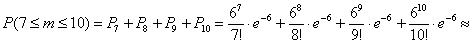
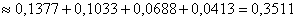– вероятность того, что за 2 часа досмотр пройдут от 7 до 10 автомобилей

б) Вычислим – среднее количество автомобилей, проходящих досмотр, за 1/2 часа.
По формуле Пуассона:
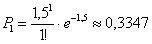– вероятность того, что за пол часа таможенный досмотр пройдёт только один автомобиль.

Ответ: а) 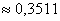, б)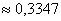

Автор: Емелин Александр

Замечание. Автор: Емелин Александр – поборник Пуассона. Но почти вся классическая теория вероятностей и математическая статистика построены на функциях Лапласа. Классические таблицы распределения Пуассона построены для 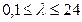, где λ=пр.

Домашнее задание.

1. Доказать, что математическое ожидание пуассоновской случайной величины равно 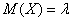и дисперсия – тому же самому значению: 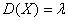. Равенство математического ожидания и дисперсии является одним из способов проверки Пуассоновского закона.

Гипергеометрическое распределение вероятностей

Пожалуй, второе по распространённости после биномиального распределения, в котором нет ничего гиперсложного. Да и сложного тоже. С гипергеометрическим законом распределения вероятностей мы неоднократно сталкивались ранее и фактически полностью построили в Примере 12 урока о классическом определении вероятности. Сформулируем задачу в общем виде и вспомним этот пример:

Пусть в совокупности из 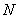объектов содержатся 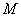объектов, обладающие некоторым признаком.

Из этой совокупности случайным образом и без возвращения извлекается 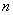объектов. Тогда

случайная величина – количество «особых» объектов в выборке – распределена по гипергеометрическому закону.

В ящике находится 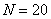деталей, среди которых 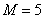бракованных. Наудачу извлекаются детали. Найти вероятность того, что:
а) обе детали будут качественными;
б) одна деталь будет качественной, а одна – бракованной;
в) обе детали бракованны

По сути дела, здесь фигурирует случайная величина – количество бракованных деталей в выборке. Прорешаем данную задачу под другим углом зрения, а именно, найдём закон распределения этой случайной величины, которая, очевидно, может принять одно из следующих значений: 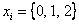. Соответствующие вероятности 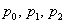определяются правилами и формулами комбинаторики и классическим определением вероятности.

Сначала вычислим количество всех возможных наборов из 2 деталей. Две детали можно выбрать

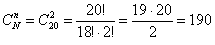способами. Дальнейшие действия удобно занумеровать:

0) 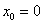(в выборке нет бракованных деталей)

способами можно извлечь 2 качественные детали

.
По классическому определению: – вероятность того, среди 2 извлечённых деталей не будет бракованных. Точнее эту вероятность следует записывать так:

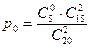. В числителе из 5 плохих выбираем 0, а из оставшихся 15 выбираем 2.

1)
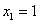
способами можно извлечь 1 качественную деталь и 1 бракованную.
По тому же определению: 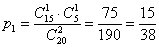– вероятность того, среди 2 извлечённых деталей будет 1 бракованная.

2) И, наконец,
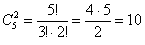способами можно извлечь 2 бракованные детали.
– вероятность того, что обе извлечённые детали будут бракованными.

Таким образом, закон распределения количества бракованных деталей в выборке:

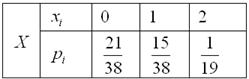
Контроль: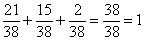

Следует отметить, что «зеркальная» случайная величина 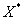– количество качественных деталей в выборке, тоже имеет гипергеометрическое распределение. Догадайтесь с одного раза, как выглядит её закон распределения. НО, к этому вопросу нельзя подходить формально! Самостоятельно разберите такую ситуацию:

Задание

Из ящика с 19 стандартными и 1 нестандартной деталью, наудачу извлекается 2 детали. Составить закон распределения случайной величины – количества стандартных деталей в выборке.

Решение и ответ в конце урока.

…Разминка прошла успешно? Отлично! Теперь разберём более содержательную задачу, в которой я расскажу вам об общих формулах и полезных технических приёмах решения. Как в передаче «Что? Где? Когда?» выносят чёрные ящики, так в теории вероятностей предлагают урны с шарами :)

Задача

Из урны, содержащей 6 белых и 4 черных шара, случайным образом и без возвращения извлекают 3 шара.

! Примечание: оговорка «без возвращения» является важной, но её часто опускают, подразумевая этот факт по умолчанию
Составить функцию распределения случайной величины – числа черных шаров среди взятых. Найти математическое ожидание и дисперсию этой случайной величины. Построить многоугольник и функцию распределению. Вычислить вероятность того, что в выборке будет не менее двух чёрных шаров. Вычислить .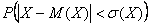

Как говорится, весь джентльменский набор. Кстати, если не нравятся шары, можете представить, что это белые и чёрные котята или…, не знаю, например, красные и чёрные карты.

Решение: поскольку в условии речь идёт о выборке объектов из совокупности и о количестве «особенных» объектов в этой выборке, то предложенная случайная величина имеет гипергеометрическое распределение вероятностей.

Обозначим исходные данные стандартными буквами:

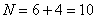– размер совокупности;
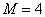– количество черных шаров в совокупности («особенный» признак);
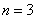размер выборки.

Очевидно, что случайная величина (кол-во чёрных шаров в выборке) принимает следующие значения:

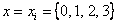
Заметьте, что этих значений может быть и меньше. В каком случае? В случае если 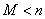, то есть, если во всей совокупности чёрных шаров МЕНЬШЕ, чем размер выборки. Так, например, если в урне всего 2 чёрных шара, то значение 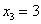отпадёт.

Для вычисления гипергеометрических вероятностей существует формула 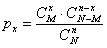, но я вам крайне советую вникать в смысл выполняемых действий. Сначала вычислим знаменатель дроби:
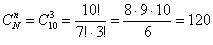способами можно выбрать 3 шара из 10. Данное значение нам потребуется при вычислении каждой вероятности :

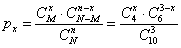0) 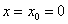(в выборке нет чёрных шаров)
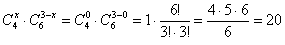способами можно выбрать 0 чёрных и 3 белых шара.
По классическому определению:
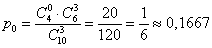– вероятность того, что в выборке будет 0 черных шаров.

Результаты лучше записывать в трёх видах: несокращённой обыкновенной дробью, сокращённой обыкновенной дробью и десятичной дробью (с 3-4-5 знаками после запятой). Это упростит решение, и скоро будет понятно, как.

Кроме того, вероятности выгодно знать заранее. Для этого можно использовать экселевскую функцию =ГИПЕРГЕОМЕТ(x; n; M; N) или сразу воспользоваться готовым расчётным макетом (Пункт 8).

Едем дальше:

1)
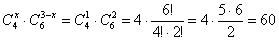способами можно выбрать 1 чёрный и 2 белых шара.
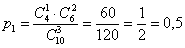– вероятность того, что в выборке окажется 1 чёрный шар.

2)
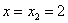
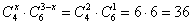способами можно выбрать 2 чёрных и 1 белый шар.
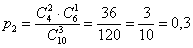– вероятность того, что в выборке окажется 2 чёрных шара.

3)
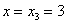
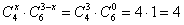способами можно выбрать 3 чёрных и 0 белых шаров.
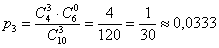– вероятность того, что в выборке будет 3 чёрных шара.

Таким образом, количество чёрных шаров в выборке распределено по следующему закону:

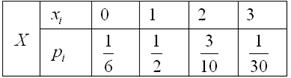
Вероятности по возможности записываем обыкновенными дробями!

Контроль: 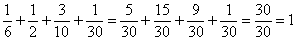, ч.т.п.

В крайнем случае можно использовать десятичные дроби (когда обыкновенные сильно наворочены), единственное, нужно следить, чтобы сумма округлённых значений равнялась единице и при необходимости «подгонять» некоторые вероятности. Однако помните, что это уже будет не точным ответом!

Но десятичные значения, безусловно, удобны для построения многоугольника распределения:

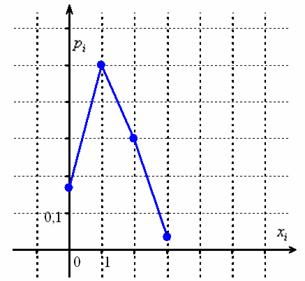
Математическое ожидание и дисперсию гипергеометрического распределения можно вычислить в обход общего алгоритма – по специальным формулам:

– среднее количество чёрных шаров в выборке (при многократном повторении таких выборок).

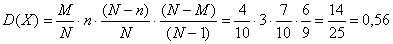– мера рассеяния количества чёрных шаров относительно матожидания.

Составим функцию распределения вероятностей. И здесь как раз пригодятся несокращённые обыкновенные дроби. Вычислим накопленные частоты:

– десятичные значения нужны для ручного построения графика.

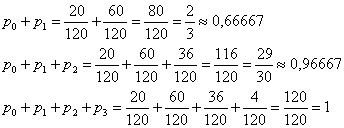
Таким образом, искомая функция:

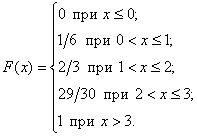
– её значения тоже записываем обыкновенными дробями! Дабы соблюсти точность.

Строим график:

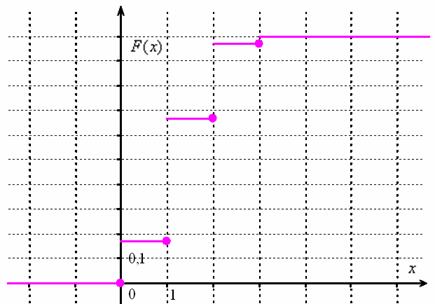
Выходим на финишную прямую. Вычислим 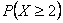– вероятность того, что в выборке будет не менее двух чёрных шаров. Это можно сделать не единственным способом. Прямым суммированием вероятностей несовместных исходов:

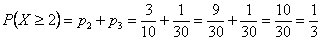
или с помощью функции распределения и штатной формулы :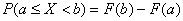

Напомню, что здесь существуют критично важные тонкости (см. по ссылке выше).

И, наконец, рассчитываем стандартную вероятность того, что значение случайной величины отклонится от математического ожидания не более чем на одно среднее квадратическое отклонение:

Готово.

Основная трудность гг-распределений состоит в технике вычислений – в них нужно грамотно управляться с дробями, которые частенько получаются страшноватыми. Ну, и конечно, не забываем о том, КАКАЯ ИМЕННО дана случайная величина. Так, в разобранном задании может быть предложено 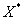– количество белых шаров в выборке, и тогда решение примет «зеркальный» характер.

Дополнительные примеры по теме можно найти в pdf-сборнике, и я поздравляют вас с освоением основных дискретных распределений. Но, само собой, существуют и другие их виды, которые не вошли в этот курс.

Далее по фарватеру непрерывная случайная величина.

Нескучного чтения!

Решение и ответ на задание:

способами можно извлечь две детали.
Случайная величина может принять одно из следующих значений: .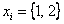

Домашнее задание.

Задание 2. Вероятность для баскетболиста попасть в кольцо при одном броске равна 0,65. Найти вероятность того, что при 1000 бросков окажется промахов

А) 362

В) от 310 до 390

С) более 360.

Задание 3. Среди 21 студента 5 отличников, 10 хорошистов и 6 удовлетвористов. Если отвечает пятёрочник, то с вероятностью 0,2 он не получит 5; если хорошист, то с вероятностью 0,5 он получит 4 или 5; если троечник, то с вероятностью 0,3 он получит выше трёх. Какой-то студент отвечает. Найти вероятность того, что он получит 4 или 5. Студент получил 4. Какова вероятность того, что он был из первой, второй или третьей группы?

Задание 4. Сколько раз надо бросить кубик, чтобы с гарантией 70% выпала хотя бы одна шестёрка?

Задание 5. Вероятность изготовления бракованных деталей при их массовом производстве равна 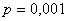. Определить вероятность того, что в партии из 800 деталей будет: а) ровно 2 бракованные, б) не более двух.

Задание 6. Вероятность выиграть по одному лотерейному билету = 0,01. Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с гарантией не меньше 95%?

Дата добавления: 2022-06-11; просмотров: 29; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!