Задача на нахождение декартовых координат
Тема : «Тригонометрические функции»
Урок №2 « Числовая окружность»
Цели урока: 1. Показать соответствие каждому действительному числу единственной точке на окружности.
Дать определение функциям синус, косинус, тангенс и котангенс.
Мы рассматриваем числовую окружность с центром в начале координат,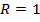 
и началом отсчета в точке 
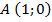, как показано на рисунке 1.
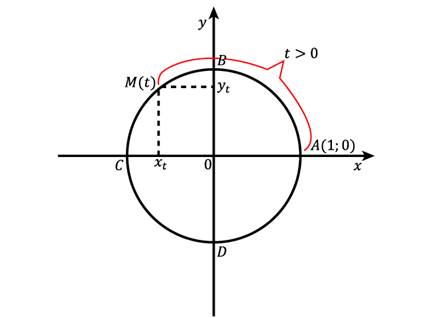
Рис. 1. Числовая окружность
Каждому действительному числу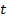 
соответствует единственная точка 
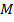на этой окружности ( рис. 1).
Каждая точка 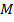имеет единственную пару декартовых координат: абсциссу 
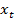и ординату 
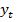(рис. 1). Имеем действительное число 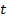, по нему находим единственную точку на окружности 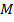, а эта единственная точка на окружности имеет единственную пару декартовых координат 
.
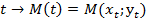Таким образом, каждому действительному числу 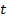сопоставляется два числа 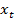и 
. И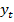меем функци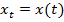и 
и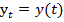 
.
Далее этим функциям будут даны специальные названия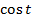 
и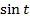 
. С каждой функцией связано две основные задачи.
Прямая задача
По заданному 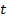найти значение функци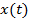и 
и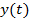 
.
Обратная задача
По заданному значению зависимой переменно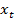й или 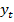найти все соответствующие значения аргумента 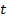. То есть найти множество всех значений аргумента, при которых зависимая переменная достигает заданного значения. Обратная задача имеет бесчисленное множество решений.
Решение вида t+2πn;
Числам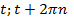 
соответствует одна и та же единственная точка 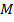на окружности, то есть 
.
|
|
|
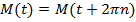Почему же точкам 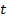и 
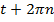соответствует одна и та же точка 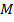на окружности?
Потому, что 
– длина единичной окружности. Ведь длина окружности 
, так как 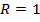. Сделав полный оборот, из точки 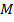мы снова попадаем в точку 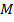. Число 
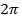далее будет называться наименьшим положительным периодом функци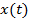и и .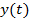
Рассмотрим еще один пример. Пусть точка 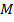соответствует на циферблате числу 1, и часовая стрелка указала на эту точку числа 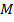, то есть на 1, один час. Но если мы находимся в комнате без окон, то мы не сможем определить, что это, час дня или час ночи. Этот пример иллюстрирует неоднозначность решения обратной задачи.
Задача 1.
Дано действительное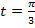 
.
Найти: место расположения точки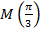 
и ее декартовы координаты 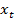и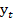 
.
Рис. 2. Первый способ нахождения точки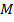
Решение
Точку 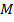можно найти несколькими способами.
Первый способ нахождения точки M
Дугу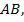 
равную 
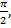разделим на 3 равные части (рис. 2). Каждая часть – это 
. Значит, точка 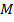имеет координату 
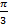, так как 
.
Второй способ нахождения точки M
Можно использовать формулу длины окружности: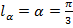 
. Стало быть, отложим угол 
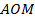и получим точку .
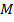Итак, расположение точки 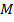найдено двумя способами.
Рис. 3.Нахождение декартовых координат точки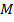
|
|
|
Найдем декартовы координаты 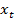и 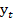. Эти координаты можно найти из прямоугольного треугольника 
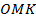. В нем известна гипотенуза 
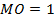, известен острый угол 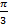(рис. 3). Значит, 
; 
.
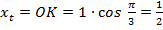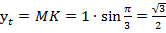Ответ: 
; 
.
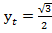Задача 2.
Дана точка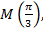 
; .
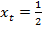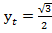Найти: координаты точек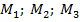 
, симметричных относительно осей координат и точке 
.
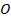Решение:
Будет очевидным, если мы каждую дугу разделим на 3 равные части, каждая часть имеет длину , учтем симметрию и в результате получим ответ.
Для точки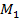 
(рис. 4): 
; ; 
.
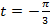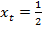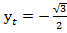Для точки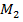 
(рис. 4): 
; 
; 
.
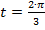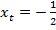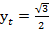Для точки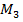 
(рис. 4): 
; 
; 
.
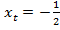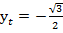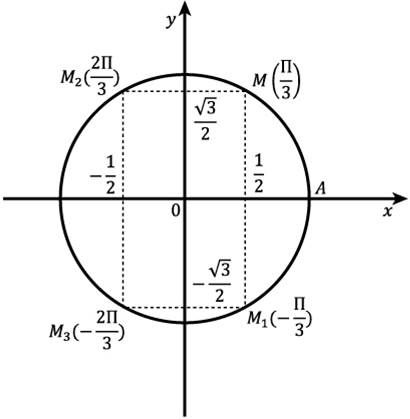
Рис. 4.Координаты симметричных точек относительно осей и относительно центра
Замечание
Криволинейных координат бесчисленное множество. Например, точка 
. Координата точки 
; 
; 
;
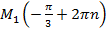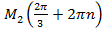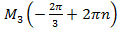Обратная задача
Дано значение абсциссы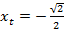 
.
Найти множество значений аргумента.
Множество значений всех 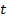. А именно, решить уравнение 
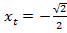. Чтобы решить это уравнение, нужно вспомнить, каким образом по заданному числу 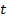мы получали точку 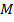и ее декартовы координаты. А именно, мы откладывали дугу, отмечали точку на окружности. Затем опускали перпендикуляры и получали декартовы координаты.
Здесь процесс выполняется в обратном направлении. Из точки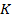 
(рис. 5) в координаты 
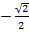восстанавливаем перпендикуляр к оси 
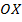и получим две точк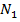и 
и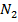 
на единичной окружности. Это единственная пара точек на окружности с заданной абсциссой 
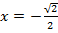. Теперь нужно определить длину дуги 
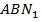(рис. 5). Рассмотрим треугольник 
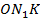. Гипотенуза – 1, катет – 
.
|
|
|
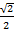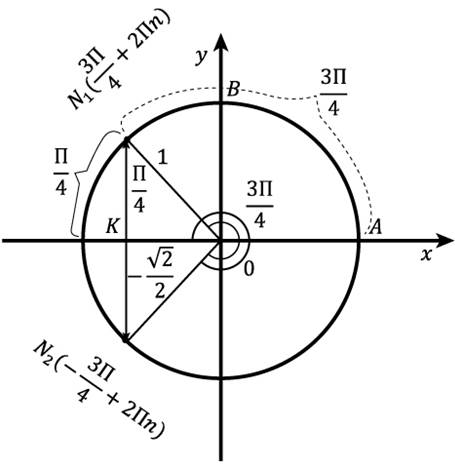
Рис. 5. Построение точки 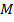и определение ее декартовых координат
Значит,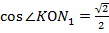 
. Отсюда 
. И соответствующая дуга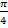 
. 
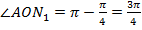, значит, первая криволинейная координата точки 
: 
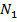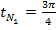, а точки : 
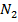.Все координаты точки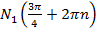 
, а все координаты точки 
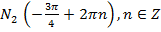(рис. 5).
Ответ: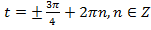 
Задача на нахождение декартовых координат
Дано: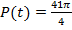 
Найти: декартовы координаты точки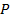 
Решение:
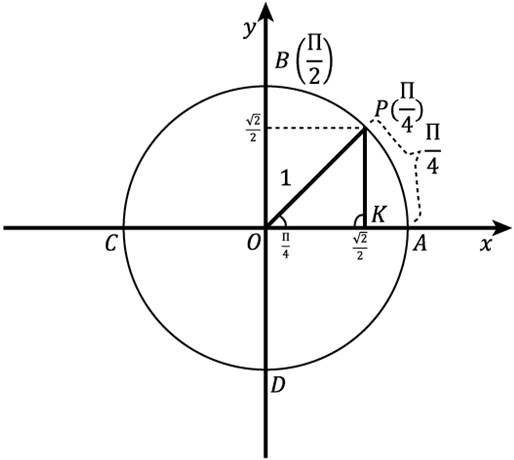
Рис. 6.Точка 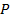на окружности
Числам 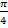и 
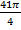соответствует одна и та же точка 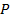на окружности. Точка 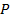– середина дуги 
(рис. 6). Декартовы координаты ее найдем из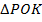 
, в нем гипотенуза – 1. Известно, что 
.
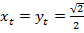Ответ: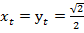 
Вывод
Мы сформулировали и рассмотрели основные задачи на числовую окружность в координатной плоскости.
Домашнее задание
Дата добавления: 2022-06-11; просмотров: 14; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!