Пример 2. Решение задачи линейного программирования
(получение дешевого металлургического сплава)
В металлургический цех в качестве сырья поступает латунь (сплав меди с цинком) четырех типов с содержанием цинка 10, 20, 25 и 40 % по цене 10, 30, 40 и 60 у.е. за 1 кг соответственно. В каких пропорциях следует переплавлять это сырье в цехе, чтобы получить сплав (латунь), содержащий 30 % цинка и при этом самый дешевый ?
Решение
Обозначим через  массу (в кг) j-го типа сырья, которое используется для получения 1 кг требуемого сплава. Тогда поставленную задачу можно формализовать следующим образом:
массу (в кг) j-го типа сырья, которое используется для получения 1 кг требуемого сплава. Тогда поставленную задачу можно формализовать следующим образом:
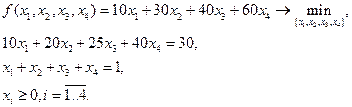
Здесь функция 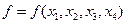 является целевой функцией нашей задачи. Точное решение задачи
является целевой функцией нашей задачи. Точное решение задачи 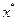 =(1/3, 0, 0, 2/3) может быть найдено аналитически, например, методом полного перебора всех возможных вершин (соответствующего графа состояний).
=(1/3, 0, 0, 2/3) может быть найдено аналитически, например, методом полного перебора всех возможных вершин (соответствующего графа состояний).
Итак, самым дешевым является сплав первого и четвертого типа сырья в отношении 1:2.
В результате получаем решение: 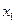 =0.3333,
=0.3333, 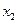 =0,
=0,  =0,
=0,  =0.6667, f=43.333333.
=0.6667, f=43.333333.
В системе Maple решаем данную задачу, используя команду minimize(f,c,vartype).
> restart: > with(simplex): > f:=10*x1+30*x2+40*x3+60*x4; > c:={10*x1+20*x2+25*x3+40*x4=30,x1+x2+x3+x4=1,x1>=0,x2>=0,x3>=0,x4>=0}; > minimize(f,c);
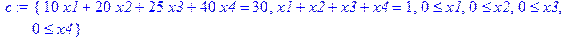
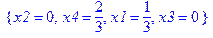
Преобразуем выражение f в отдельную процедуру с целью последующего использования в вычислениях:
> fqproc:=codegen[makeproc](f,[x1,x2,x3,x4]);
> x1:=1/3; x2:=0; x3:=0; x4:=2/3; > f_min:=fqproc(x1,x2,x3,x4); evalf(%);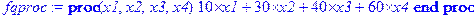
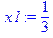

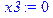
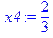


Транспортная задача
В транспортной задаче, которая является разновидностью задачи линейного программирования и решается соответствующими методами, требуется найти оптимальный план перевозок некоторого продукта от заданного множества производителей, занумерованных числами 1,2,…,M к множеству потребителей, занумерованных числами 1,2,…,N.
Производственные возможности i-го производителя заданы объемом производимого продукта -  . Спрос j-го потребителя на этот продукт задается числом
. Спрос j-го потребителя на этот продукт задается числом 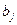 .
.
Обозначим планируемый объем перевозок от i-го производителя к j-ому потребителю как 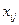 . В этих условиях должны быть выполнены очевидные балансовые соотношения:
. В этих условиях должны быть выполнены очевидные балансовые соотношения:
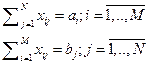 (1)
(1)
Для существования допустимого плана перевозок должен выполняется общий баланс между спросом и потреблением:
 .
.
При этом транспортную задачу называют сбалансированной.
Можно убедиться, например, что в сбалансированной транспортной задаче величины
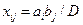 (2)
(2)
представляют в совокупности допустимый вариант перевозок, т.к. удовлетворяют ограничениям (1).
Целью решения транспортной задачи является минимизация суммарных транспортных расходов.
Если предположить, что стоимость перевозки продукта линейно зависит от объема перевозки и характеризуется числами 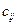 , где
, где 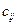 - стоимость перевозки единицы продукта от i-го производителя к j-му потребителю, а
- стоимость перевозки единицы продукта от i-го производителя к j-му потребителю, а 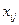 - объемы перевозок, то целевая функция в транспортной задаче принимает вид:
- объемы перевозок, то целевая функция в транспортной задаче принимает вид:
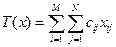 (3)
(3)
и задача заключается в минимизации (3), т.е.
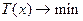 , (4)
, (4)
при выполнении ограничений (1) и условии неотрицательности всех переменных 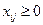 .
.
Переменные 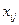 можно представить в виде матрицы (таблица 1):
можно представить в виде матрицы (таблица 1):
| Таблица 1. Матрица объемов перевозок. | ||||||
| 1 | 2 | ... | N | ||
| 1 | 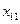
| 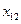
| ... | 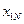
| ||
| 2 | 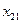
| 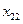
| ... | 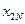
| ||
| ... | ... | ... | ... | ... | ||
| M | 
| 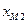
| ... | 
| ||
или, более традиционную, в виде вектора 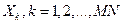 ,развернув в этот вектор вышеприведенную таблицу 1. При естественном обходе таблицы 1 (допустим по столбцам) матрица ограничений (1) примет специфический вид, приведенный в таблице 2.
,развернув в этот вектор вышеприведенную таблицу 1. При естественном обходе таблицы 1 (допустим по столбцам) матрица ограничений (1) примет специфический вид, приведенный в таблице 2.
| Таблица 2. Матрица ограничений транспортной задачи. | |||||||||||||
| 1 | 1 | ... | 1 | ||||||||||
| 1 | 1 | ... | 1 | ||||||||||
| ... | |||||||||||||
| 1 | 1 | ... | 1 | ||||||||||
| 1 | 1 | ... | 1 | ||||||||||
| 1 | 1 | ... | 1 | ||||||||||
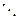
| 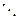
| ... | 
| ||||||||||
| 1 | 1 | ... | 1 | ||||||||||
Видно, что матрица ограничений транспортной задачи обладает рядом характерных особенностей, из которых отметим следующие:
§ большая часть ее элементов равна нулю;
§ среди ненулевых элементов много одинаковых.
Первое свойство матрицы называют разреженностью, а последнее свойство называют сверхразреженностью.
Для характеризации разреженности используют две меры - количество ненулевых элементов в матрице ограничений и их отношение к общему числу элементов матрицы. Последняя характеристика называется плотностью. Для транспортной задачи плотность d равна  и падает с ростом размерности задачи, что вообще типично для задач линейного программирования.
и падает с ростом размерности задачи, что вообще типично для задач линейного программирования.
Описанный вариант транспортной задачи называется транспортной задачей в матричной постановке. В такой задаче разрешаются связи между произвольными поставщиками и потребителями.
На практике зачастую некоторые связи между определенными поставщиками и потребителями невозможны или нежелательны из-за разного рода внемодельных соображений (отсутствие дорог, специфика погрузочно-разгрузочного оборудования и тому подобное).
Чтобы отобразить подобного рода ситуации, транспортную задачу формулируют в сетевом виде, задавая и фиксируя структуру связей «поставщик» « «потребитель». Связи можно задать списком, приведенным в таблице 3, используя вместо имен потребителей и поставщиков их уникальные индексы из некоторого реестра.
| Таблица 3. Список транспортных связей | |||
| п/п | Поставщик | Потребитель | Стоимость перевозки |
| 1 | Владивосток | Москва | 134 |
| 2 | Хабаровск | Владивосток | 27 |
| ... | ... | ... | ... |
| 127 | Якутск | Магадан | 98 |
С i-ой связью можно ассоциировать соответствующую переменную 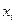 , которая имеет смысл объема перевозок по этому направлению.
, которая имеет смысл объема перевозок по этому направлению.
Если множество связей, ведущих к потребителю i, обозначить через 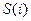 , а множество связей, ведущих к поставщику j, обозначить через
, а множество связей, ведущих к поставщику j, обозначить через  , то балансовые уравнения запишутся в виде:
, то балансовые уравнения запишутся в виде:
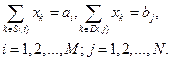
Наглядно транспортную задачу в сетевой постановке лучше всего представить в виде графа - некоторого множества вершин, соединенных дугами, обозначающими транспортные связи.
Задача
В трех хранилищах горючего ежедневно хранятся 20, 10 и 15 тонн горючего. Это горючее каждый день перевозят на четыре топливозаправочные станции в количествах, равных соответственно 10, 15, 10 и 10 тонн. Стоимости перевозок 1 тонны горючего из хранилищ к заправочным станциям задаются в виде стоимостной матрицы (в у.е.):
| Заправочная станция | ||||
| Хранилище | 1 | 2 | 3 | 4 |
| 1 | 9 | 7 | 5 | 3 |
| 2 | 1 | 2 | 4 | 6 |
| 3 | 8 | 10 | 12 | 1 |
Необходимо составить такой план перевозок горючего, при котором общая стоимость перевозок была бы минимальной.
Дата добавления: 2022-06-11; просмотров: 128; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
