Дифференциальное уравнение конвективного теплообмена
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
“Кубанский государственный технологический университет”
(ФГБОУ ВО “КубГТУ”)
Реферат по дисциплине:
«Математическое моделирование в нефтегазовой отрасли»
Выполнил:
Ст.гр 20-ОЗНМ-НД3
Макеев П.Е.
Проверил:
Запорожец Е.П.
Краснодар
2020
Содержание
Введение…………………………………………………………………………...3
1.Этапы создания математической модели…………………………...…………4
2. Закон Фурье…………………………………………………………………..…6
3. Дифференциальное уравнение конвективного теплообмена………………..7
Заключение…………………………………………………………………….....10
Введение
Метод математического моделирования, представляющий собой количественное описание изучаемых явлений на языке математики, широко применяется для исследования всевозможных явлений природы и общественной жизни. Этот «третий путь познания» сочетает в себе достоинства как теории, так и эксперимента. С одной стороны, работая не с самим объектом, а с ее моделью, мы можем относительно быстро и без существенных затрат исследовать его свойства и поведение в любых мыслимых ситуациях (преимущества теории). С другой стороны, вычислительные эксперименты с моделями объектов позволяют, опираясь на мощь современных вычислительных методов и вычислительной техники, подробно и глубоко изучать объекты в достаточной полноте, недоступной чисто теоретическим исследованиям (преимущества эксперимента)
|
|
|
Этапы создания математической модели
Построение математических моделей объектов и систем осуществляется последовательно по этапам, на каждом из которых проводятся соответствующие проверки, а также производится документирование выполненных действий.
Различают 3 этапа построения математических моделей (рисунок 2):
1.Формулировка замысла модели.
2.Реализация модели.
3.Получение и анализ результатов.
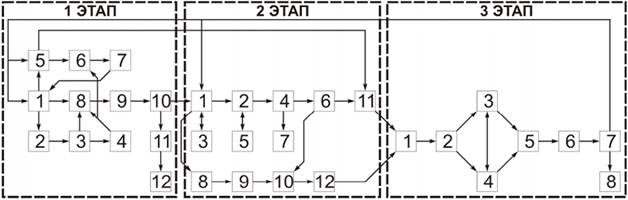
Рисунок 2. Блок-схема этапов построения математической модели
1) На первом этапе строится предполагаемая модель в абстрактных терминах.
1. Постановка задачи.
2. Определение требований к информации.
3. Сбор информации.
4. Выдвижение гипотез и предположений (при недостатке информации).
5. Анализ проблем (задачи).
6. Определение параметров и переменных (согласно обозначениям по ГОСТ).
7. Выбор критериев эффективности (например, надёжность, качество работы, время, вероятности различных событий, характеристики времени функционирования, характеристики измерений, ошибки и так далее). Для каждого из критериев создается словесная формулировка, затем математическое описание.
8. Составление, обоснование модели.
9. Определение аппроксимирующих выражений (математическая модель системы должна быть детерминированная, стохастическая, усреднённая).
10. Описание замысла модели.
11. Проверка модели (осуществляется компетентными людьми).
12. Документирование первого этапа.
|
|
|
2) На втором этапе необходимо проверять соответствие размерностей слагаемых в уравнениях.
1.Вывод детальных математических уравнений модели.
2.Составление блок-схемы модели.
3.Проверка блок-схемы (включает в себя анализ значений рассматриваемых характеристик с целью определения для системы резервов и допустимых интервалов изменения параметров).
4.Составление блок-схемы программы.
5.Проверка блок-схемы программы.
6.Составление программы математической модели.
7.Проверка программы математической модели.
8.Выбор вычислительных средств.
9. Составление спецификаций для программ (каждый параметр должен быть описан, а также описана область его применения).
10.Составление плана рабочих расчётов.
11.Планирование эксперимента с моделью.
12.Документирование второго этапа.
|
|
|
3) На третьем этапе проводится тщательная проверка созданной модели, а также проводятся специальные испытания.
1.Выполнение рабочих расчётов.
2.Анализ результатов (теоретический и экспериментальный анализ).
3.Получение поверхностей отклика.
4.Вывод уравнения регрессии.
5.Оценка обобщённых результатов.
6.Получение выводов.
7.Выдача рекомендаций по применению модели.
8.Документирование третьего этапа.
При построении модели возможно возвращение на предыдущие этапы в связи с получением неудовлетворительных результатов или с возникновением ошибок. Проектирование осуществляется до тех пор, пока не будут устранены все недостатки. Полученная модель должна удовлетворять всем основным выбранным критериям адекватности.
Закон Фурье
Теплопроводность представляет собой форму передачи теплоты путем непосредственного соприкосновения отдельных частиц тела, имеющих различную температуру. При этом процесс теплообмена происходит вследствие передачи энергии микродвижения одних элементарных частиц другим.
|
|
|
Согласно гипотезе Фурье, количество теплоты проходящей через элемент изотермической поверхности 
за промежуток времени 
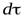, пропорционально температурному градиенту
,
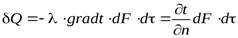где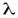 
–коэффициент теплопроводности,
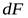– элементарная площадь поверхности, м2;
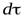– время передачи теплоты,
Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности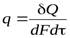 
, называется плотностью теплового потока.
Количества теплоты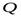 
, проходящее в единицу времени через изотермическую поверхность 
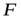, называется тепловым потоком (Дж/с =Вт):
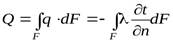
Величина теплового потока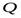 
и плотность теплового потока 
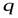являются векторами, за положительное направление которых принимают направление по нормали к изотермической поверхности в сторону уменьшения температуры.
Скалярная величина вектора плотности теплового потока будет равна:
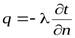
Скалярная величина вектора теплового потока будет равна:
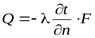
Знак минус в правой части уравнений указывает на то, что тепловой поток и температурный градиент как векторы имеют противоположные направления.
Коэффициент теплопроводности - тепловой поток, передаваемый через единичную поверхность при единичном значении температурного градиента
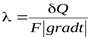
Для каждого тела 
имеет свое численное значение и, зависит от природы, пористости, влажности, давления, температуры и других параметров. Численное значение определяется опытным путем (в справочных таблицах). При выводе уравнения принято, что 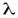не зависит от температуры. Как показывают опыты, для многих материалов, зависимость коэффициента теплопроводности от температуры можно принять линейной во всем рассматриваемом интервале т-р:
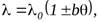
где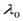 
– коэффициент теплопроводности при температуре 
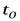(0°C);
b – постоянная, характеризующая приращение (уменьшение) материала при повышении его температуры на 1°C.
Наихудшие - газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и изменяется в пределах 0,005 – 0,5 Вт/(м·°C).
Наилучшими проводниками теплоты являются металлы, у которых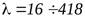 
Вт/(м·°C). У большей части металлов с возрастанием температуры он уменьшается.
Дифференциальное уравнение конвективного теплообмена
При конвективном теплообмене тепло распространяется в жидкости одновременно теплопроводностью и конвекцией. Процесс распространения тепла теплопроводностью описывается дифференциальным уравнением вида
.
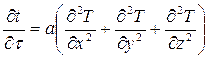Левая часть этого уравнения представляет локальное изменение температуры элемента, выделенного в неподвижной среде.
При конвективном теплообмене элемент перемещается из одной точки пространства в другую. В этом случае изменение температуры элемента может быть выражено при помощи субстациональной производной, учитывающей одновременно изменения параметра во времени и в пространстве, связанные с перемещением элемента из одной точки в другую. Субстанциональная производная, характеризующая полное изменение температуры движущего элемента, может быть записана в следующем виде:
.
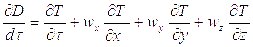Если в уравнении теплопроводности заменить локальное изменение температуры полным, то можно получить дифференциальное уравнение конвективного переноса тепла Фурье-Кирхгофа:
.
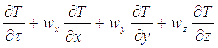
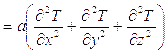Для полного математического описания это уравнение должно быть дополнено уравнением, характеризующим условия на границе раздела движущейся среды и твердого тела.
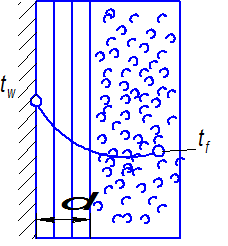
У поверхности твердого тела, находящегося в движущейся среде, всегда имеется пограничный слой толщиной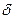 
, через который тепло распространяется теплопроводностью (рис. 3.3).
Количество переданного через этот слой тепла при его распространении от теплообменной поверхности к ядру жидкостного потока можно определить по закону Фурье
.
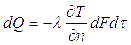Это же количество тепла можно найти по закону Ньютона:
.
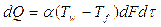Приравнивая правые части последних равенств, получаем уравнение, характеризующее условия теплообмена на границе раздела движущейся среды и твердого тела:
.
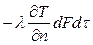
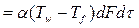Полученное уравнение и дифференциальное уравнение конвективного массообмена в полной мере описывают процесс, но для их решения необходимо еще знать проекции скоростей потока жидкости по соответствующим координатам.
С этой целью система уравнений должна включать дифференциальные уравнения движения и неразрывности. Но, как уже было сказано выше, такая система уравнений не имеет аналитического решения. Не имеет аналитического решения также система с дифференциальным уравнением конвективного теплообмена.
Таким образом, аналитически не может быть установлено ни температурное поле в движущейся среде, ни величина теплового потока. Для решения конкретных инженерных задач приходится прибегать к эксперименту и обобщениям с использованием методов теории подобия.
Заключение
Модель нужна для того, чтобы:
Понять, как устроен конкретный объект: какова его структура, внутренние связи, основные свойства, законы развития, саморазвития и взаимодействия с окружающей средой;
Научиться управлять объектом или процессом, определять наилучшие способы управления при заданных целях и критериях;
Прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект.
Дата добавления: 2022-01-22; просмотров: 25; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!