Важным условием динамического программирования является аддитивный характер задачи.
Слайд 1. (титульный) – Олег
Слайд 2. (предпосылки к появлению DP) – Олег
В настоящее время многие организации в своей деятельности сталкиваются с математическими моделями. Математическая модель – это система математических уравнений, неравенств, формул и различных математических выражений, описывающих поведение реального объекта.
Описание задачи или процесса при помощи математической модели позволяет свести решение, например, экономической задачи к математическому анализу.
В данной работе будет рассматриваться один из подходов к решению такого рода задач – динамическое программирование. Предпосылками к его появлению можно считать следующие факторы:
1. Необходимость поиска оптимального решения задач, в том числе экономических.
2. Для снижения емкости вычислений желательно использование принципа «разделяй и властвуй».
3. Формулировка Ричардом Беллманом принципа оптимальности, который гласит: «Оптимальное поведение обладает тем свойством, что каким бы ни было первоначальное состояние системы и первоначальное решение, последующее решение должно определять оптимальное поведение относительно состояния, полученного в результате первоначального решения».
Слайд 3. (постановка задачи и особенности DP) – Олег
Динамическое программирование представляет собой математический аппарат, который используется для решения некоторого класса задач путем их разделения на небольшие и менее сложные задачи. При этом отличительной особенностью является решение задач по этапам, через фиксированные интервалы, промежутки времени, что и определило появление термина динамическое программирование.
|
|
|
Следует заметить, что методы динамического программирования успешно применяются и при решении задач, в которых фактор времени не учитывается. В целом математический аппарат можно представить как пошаговое или поэтапное программирование.
При этом, как и в задачах, решаемых методами линейного программирования, ограничения могут быть даны в виде равенств или неравенств. Однако если в задачах линейного программирования зависимости между критериальной функцией и переменными обязательно линейны, то в задачах динамического программирования эти зависимости могут иметь еще и нелинейный характер.
Таким образом, динамическое программирование в широком смысле представляет собой оптимальное управление процессом, посредством изменения управляемых параметров на каждом шаге, и, следовательно, воздействуя на ход процесса, изменяя на каждом шаге состояние системы.
Требуется определить такое управление Х*, переводящее систему из начального состояния S 0 в конечное состояние Sn , при котором целевая функция принимает наибольшее (наименьшее) значение F ( S 0 , X *) → extr .
|
|
|
1. Задача оптимизации формулируется как конечный многошаговый процесс управления;
2. Целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага:
F = ∑ Fk (Sk−1, x k ) → extremum ;
3. Выбор управления хk на каждом шаге зависит только от состояния системы к этому шагу Sk−1, и не влияет на предшествующие шаги (нет обратной связи);
4. Состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk-1 и этого управляющего воздействия хk (отсутствие последействия) и может быть записано в виде уравнения состояния: Sk= fk (Sk-1, хk), k = 1, n;
5. На каждом шаге управление хk зависит от конечного числа управляющих переменных, а состояние системы Sk зависит от конечного числа параметров;
6. Оптимальное управление представляет собой вектор X*, определяемый последовательностью оптимальных пошаговых управлений: X = (х*1, х*2, …, х*k, …, х*n), число которых и определяет количество шагов задачи.
Слайд 4. (Общий принцип работы DP) – Вовенцио
Динамическое программирование пользуется следующими свойствами задачи:
|
|
|
- перекрывающиеся подзадачи;
- оптимальная подструктура;
- возможность запоминания решения часто встречающихся подзадач.
Задачи динамического программирования являются многоэтапными или многошаговыми. При использовании этого метода задача разбивается на количество шагов по числу неизвестных. На каждом шаге решается задача оптимизации только по одной переменной. Таким образом, процесс нахождения оптимального плана многомерной задачи распадается на ряд более простых одномерных задач оптимизации.
Принимая решение на i-ом шаге надо учитывать его влияние на будущее, т.е. учитывать влияние принимаемого решения на эффективность последующих шагов. Имеется единственный шаг в решении задачи, в котором можно планировать без учета влияния решения на последующие шаги – это последний шаг. Его можно планировать так, чтобы он изолированно принес наибольшую выгоду. Поэтому процесс поиска оптимального решения начинается от конца к началу.
Слайд 5. (Функциональное уравнение Беллмана) – Вовенцио
Для планирования последнего шага необходимо знать, что вышло в конце предыдущего шага. Чтобы решить эту задачу, находят варианты условий последнего n-го шага, которые соответственно равны вариантам окончания (n-1)-го шага. Каждый вариант используется для нахождения наиболее выигрышного решения для последнего шага. Существует функциональное уравнение Беллмана для последнего шага, по которому определяется это решение:
|
|
|
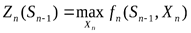
Где Xn – управление системой на n-ом шаге,
fn – целевая функция на n-ом шаге,
Sn-1 – состояние системы в после выполнения (n-1)-го шага.
Для (n-1)-го шага уравнение Беллмана выглядит как:
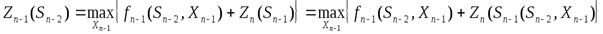
То есть для (n-1)-го шага необходимо найти такое управление Xn-1 , чтобы сумма выигрышей на (n-1)-ом шаге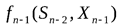 
и на n-ом шаге 
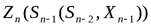была максимальна. И т.д.
На k-ом шаге (уравнение Беллмана в общем виде)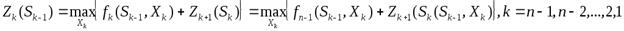 
то есть на k-ом шаге надо так подобрать управление 
, чтобы сумма выигрышей на k-ом шаге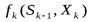 
и на n-k последующих шагах 
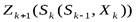была максимальна.
При динамическом программировании многошаговый процесс проходят два раза:
1) от конца к началу – находят условные оптимальные решения на каждом шаге с учетом выигрыша на всех шагах, начиная с данного до конца;
2) от начала к концу – находят оптимальные шаговые решения на всех шагах.
Слайд 6. (Пример: задача Фибоначчи) – Олег
Требуется найти значение последовательности чисел Фибоначчи для F{5}, при этом, зная, что F{3}=F{2}+F{1} и F{4}=F{3}+F{2}}, даже в таком тривиальном случае вычисления всего двух чисел Фибоначчи мы уже посчитали F{2} дважды. Если продолжать дальше, то получается следующее: простой рекурсивный подход будет расходовать время на вычисление решения для задач, которые он уже решал. Чтобы избежать такого хода событий, мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется мемоизацией.
Слайд 7. (Достоинства и недостатки) – Олег
Среди достоинств можно выделить:
1. На каждом этапе решается задача поиска экстремума лишь по части переменных, следовательно, размерность этих задач по сравнению с исходной значительно ниже. Это позволяет упростить поиск оптимальных значений искомых переменных.
2. Решение задач, которые не могут быть решены другими методами.
3. Простая реализация на ЭВМ.
Среди недостатков выделяют:
1. Отсутствие универсального алгоритма, который был бы пригоден для решения всех задач рассматриваемого класса. Алгоритмы ДП объединены лишь общей идеей, и в каждом конкретном случае должны формироваться применительно к специфике прикладной задачи.
2. При большой размерности исходной задачи эти алгоритмы требуют значительных ресурсов ЭВМ.
Слайд 8. (Классические и практические задачи ДП) – Вова
Классические задачи динамического программирования:
· Задача о наибольшей общей подпоследовательности: даны две последовательности, требуется найти самую длинную общую подпоследовательность.
· Задача поиска наибольшей увеличивающейся подпоследовательности: дана последовательность, требуется найти самую длинную возрастающую подпоследовательность.
· Задача о редакционном расстоянии (расстояние Левенштейна): даны две строки, требуется найти минимальное количество стираний, замен и добавлений символов, преобразующих одну строку в другую.
· Задача о вычислении чисел Фибоначчи
· Задача о порядке перемножения матриц: даны матрицы A1, …, An, требуется минимизировать количество скалярных операций для их перемножения.
· Задача о рюкзаке: из неограниченного множества предметов со свойствами «стоимость» и «вес» требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при ограниченном суммарном весе.
· Алгоритм Флойда — Уоршелла: найти кратчайшие расстояния между всеми вершинами взвешенного ориентированного графа.
· Алгоритм Беллмана — Форда: найти кратчайший путь во взвешенном графе между двумя заданными вершинами.
· Максимальное независимое множество вершин в дереве: дано дерево, найти максимальное множество вершин, никакие две из которых не связаны ребром.
Практические задачи динамического программирования:
· Задача распределения средств между предприятиями. Распределении инвестиций между предприятиями П1, П2,..., Пn. Инвестируемая сумма E усл. ден. ед.
· Задача распределения ресурсов. Планируется работа двух предприятий на n лет. Начальные ресурсы равны s0
· Задача замены оборудования.
· Складская задача. Составить оптимальную программу выпуска продукции X, которая минимизирует суммарные издержки предприятия.
· Задача найма работников на предприятие.
Слайд 9. (Классификация DP по порядку действий) – Вова
Динамическое программирование обычно придерживается двух подходов к решению задач:
1. Нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений уже решенных подзадач.
2. Восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.
Особенно эффективно применение динамического программирования тогда, когда по существу задачи нужно принимать решения поэтапно. Например, рассмотрим простой пример задачи замены и ремонта оборудования. Допустим, на литейной машине завода по изготовлению шин делают одновременно шины в двух разных формах. В том случае, если одна из форм выходит из строя, приходится машину разбирать. Понятно, что иногда выгоднее заменить и вторую форму для того, чтобы не разбирать машину на случай, если и эта форма окажется неработоспособной на следующем этапе. Тем более, бывает проще заменить обе работающие формы до того, как они начнут выходить из строя. Метод динамического программирования определяет наилучшую стратегию в вопросе о замене таких форм, учитывая все факторы: выгоду от продолжения эксплуатации форм, потери от простоя машины, стоимость забракованных шин и другое.
Важным условием динамического программирования является аддитивный характер задачи.
Слайд 10 и 11. (Вывод и спасибо за внимание) - Олег
Таким образом, динамическое программирование является методом математического решения задач, при помощи которого можно найти оптимальное решение экономических и технических задач. Как и любой вид программирования он имеет свои достоинства и недостатки, а также широко используется при решении различных задач.
Дата добавления: 2022-01-22; просмотров: 19; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!