Оздоровительные паузы в соответствии с ЗОЖ)

Технологическая карта урока №110 по предмету БД.3 Математика

Тема: Понятие о производной функции, её физический и геометрический смысл. Уравнение касательной к графику функции.

Тип занятия: урок изучения нового материала (лекция)

Метод обучения: информационно-развивающий метод (объяснение нового материала)

Формы учебной деятельности: коллективно-групповое занятие.

Цели занятия:

учебная - познакомить обучающихся с понятием производной функции, её физическим и геометрическим смыслом;

развивающая - формирование умений применять приемы сравнения, обобщения, выделения главного, логически излагать мысли, делать выводы, развивать речь, внимание и память.

воспитательная - способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

Формируемые на уроке ПК и ОК:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

Информационно-методическое обеспечение:

Математика: алгебра и начала математического анализа, геометрия: учеб. для студ. учреждений сред. проф. образования / М.И. Башмаков. 3-е изд., стер. – М.: Издательский центр «Академия», 2017

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни / [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – М.: Просвещение, 2014

Материально-техническое обеспечение: ноутбук, проектор, белая доска, маркеры для белой доски, мел.

Структура урока

1.Организационный момент                                                                        2^/

-создание благоприятной психологической атмосферы;

-проверка организации рабочих мест обучающихся;

-проверка внешнего вида;

-проверка списочного состава обучающихся и заполнение журнала, рапорта и рапортички.

2. Сообщение темы, цели и задач урока.                                                     1^/

Сообщаю тему урока и объявляю, что они научатся находить производные различных функций. Производные функций будут применяться на протяжении почти всего курса математического анализа.

3. Проверка домашнего задания и самостоятельной работы обучающихся:    5^/

Обучающиеся сообщают ответы на заданные упражнения и проблемы при их решении.

4. Актуализация опорных знаний по теме урока:                                              4^/

Обучающиеся вспоминают, что такое пределы последовательностей, функций.

5. Мотивация учебной деятельности по теме урока                                          1^/

Эта тема – начальная в курсе предмета «Начала математического анализа», поэтому понимание темы необходимо при изучении всего предмета.

6.  Основная часть:                                                                                   27^/

Задачи, приводящие к понятию производной функции.

Рассмотрим две задачи.

ЗАДАЧА 1. Пусть материальная точка движется по прямой по закону
s(t) = 4t²,                              (1)

где s — путь, пройденный точкой за время t (t ≥ 0). Путь, время и скорость измеряются соответственно в метрах, секундах и в метрах в секунду.

Вычислим сначала среднюю скорость этой точки за промежуток времени от t₁ = 2 до t₂ = 5. Путь, пройденный точкой за время t₁ = 2, равен

s(2) = 4 ∙ 2² = 16, а путь, пройденный ею за время t₂ = 5, равен s(5) = 4 ∙ 5² = 100.

Тогда путь, пройденный точкой за промежуток времени от t₁ = 2 до t₂ = 5, равен

s(5) – s(2) = 100 – 16 = 84.

Средняя скорость точки за промежуток времени от t₁ = 2 до t₂ = 5

равна υ_ср = 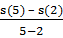 =  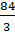= 28.

Вычислим теперь среднюю скорость υ_ср этой точки за промежуток времени от t до t + Δt. Путь, пройденный точкой за время t, равен s(t) = 4t², а путь, пройденный ею за время t + Δt, равен s(t + Δt) = 4(t + Δt)². Тогда путь, пройденный точкой за промежуток времени от t до t + Δt > равен

Δs = s(t + Δt) – s(t) = 4(t + Δt)² – 4t² = (8t + 4Δt) Δt.

Средняя скорость точки за промежуток времени от t до t + Δt равна

υ_ср = 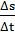 =  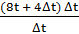= 8t + 4Δt

Итак, средняя скорость υ_ср есть сумма двух слагаемых. Первое не зависит от Δt, а второе зависит от Δt, и при этом оно мало для малых Δt.

Таким образом, можно считать, что при малых Δt средняя скорость υ_ср приближенно равна числу 8t, т. е. υ_ср ≈ 8t.

Число υ = 8t есть, очевидно, предел, к которому стремится υ_ср при Δt → 0. Его называют мгновенной скоростью точки, движущейся по закону (1), в момент времени t.

В общем случае если точка движется по прямой по закону s(t) = f(t), то ее мгновенной скоростью υ в момент времени t называют предел (если он существует), к которому стремится ее средняя скорость на промежутке времени [t; t + Δt] при Δt → 0:

υ =  =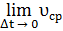

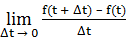
Величину Δt называют приращением времени, а величину Δf = f(t + Δt) – f(t) — приращением пути. Другими словами, мгновенной скоростью движущейся точки в момент времени t называют предел (если он существует) отношения приращения пути к приращению времени, когда последнее стремится к нулю:

υ =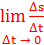

ЗАДАЧА 2. Пусть кривая Г есть график непрерывной на интервале (a; b) функции
у = f(x) (рис. 93 или 94). Зададим на кривой Г точку А, имеющую абсциссу х и ординату у, и точку С, имеющую абсциссу х + Δх (Δх ≠ 0) и соответствующую ординату у + Δу = f(x) + Δf, где Δf = f(x + Δх) – f(x).

      

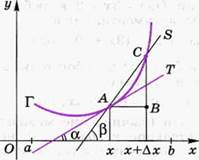
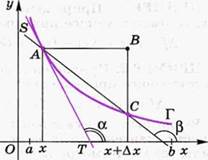
Секущая S, проходящая через точки А и С, образует с положительным направлением оси Ох угол β (здесь и далее угол между положительным направлением оси Ох и прямой откладывается от положительного направления оси Ох против часовой стрелки).

На рисунках 0 < β <  и  < β < π соответственно.

Из рисунков следует, что

tg β =  =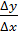

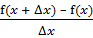
Будем устремлять Δх к нулю; тогда вследствие непрерывности функции
у = f(x) также будет стремиться к нулю Δу и точка С, двигаясь по кривой Г, будет стремиться к точке А. Если окажется (а этого может и не быть!), что при этом при любом способе стремления Δх к нулю отношение 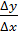 стремится к одному и тому же пределу (числу) k:

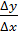 → k (Δх → 0)

то тогда и угол β будет стремиться к некоторому, отличному от  углу α. Вместе с β и секущая S, вращаясь около точки А, будет стремиться занять в пределе положение прямой Т, проходящей через точку А под углом α к положительному направлению оси Ох. Но тогда прямая Т есть касательная к кривой Г в точке А и

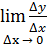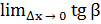 =  = tg α

На рисунках 0 < β <  и  < β < π соответственно.

Мы установили, что если при Δх → 0 отношение 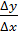 стремится к конечному пределу, то кривая Г имеет в точке А касательную, тангенс угла которой с положительным направлением оси Ох равен этому пределу.

 

Теперь рассмотрим функцию у = f(x), определенную в некоторой окрестности точки х. Выберем в этой окрестности произвольную точку (число), отличающуюся от х на Δх, т. е. точку х + Δх.

Число Δх называют приращением аргумента, а разность значений функции в точках х + Δх и х называют приращением функции. Приращение функции у = f(x) в точке х обозначают Δf или Δу:

Δу = Δf = f(x + Δх) – f(x)

 

ПРИМЕР 1. Приращение функции f(х) = 3х + 2 в любой точке х, соответствующее приращению Δх аргумента, равно

Δf = f(x + Δх) – f(x) = (3(x + Δх) + 2) – (3x + 2) = 3Δх

Выше были рассмотрены две задачи (вычисление мгновенной скорости и тангенса угла наклона касательной к графику функции). Несмотря на то что все они относятся к различным областям знания — механике, геометрии, их решение привело к одной и той же математической операции, которую нужно произвести над функцией: надо найти предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю. Число задач, решение которых приводит к той же операции, очень велико. К ним относятся, например, задачи о скорости химической реакции, о плотности неравномерно распределенной массы, о силе тока и др.

Эта операция получила в математике специальное название — дифференцирование функции. Результат ее выполнения называют производной.

Производной функции у = f(х), заданной на некотором интервале (а; b), в точке х этого интервала, называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производная функции f(х) при данном х из интервала (а; b) (если она в этой точке х существует) есть число. Если производная функции f (х) существует при каждом значении х из интервала (а; b), то производная есть функция от х, определенная на интервале (а; b).

Производную функции f(х) обозначают f '(х) и говорят: «эф штрих от икс». Следовательно,

f '(х) =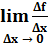

Широко употребляются и другие обозначения производной:

у', , , , .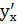

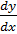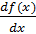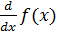Предел  (если он существует) в точке х, когда рассматривается только Δх > 0 или Δх < 0, называют соответственно правой производной и левой производной функции f в точке х. Про функцию f(х), заданную на отрезке [а; b], принято говорить, что она имеет производную на этом отрезке, если она имеет производную в любой точке интервала (а; b) и, кроме того, правую производную в точке а и левую — в точке b.

Найдем производные для некоторых функций f(х), определенных на интервале (- ; + ).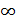

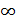1. f(x) = х. Для любой точки х приращение функции f равно

Δf = f(x + Δх) - f(x) = (х + Δх) - х = Δх.

Поэтому 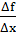 =  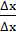= 1. Следовательно, производная функции f(x) = х в любой точке х равна 1, т. е. х' = 1.

2. f(x) = С. Постоянную можно рассматривать как такую функцию от х, которая равна одному и тому же числу С для любого х из интервала
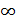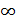(- ; + ). Тогда для этой функции приращение функции f равно

Δf = f(x + Δх) - f(x)  = С - С = 0.

Поэтому 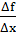 =  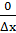= 0. Следовательно, производная функции f(x) = С в любой точке х равна 0, т. е. С' = 0.

Как следует из рассмотренных в начале данного пункта задач, справедливы следующие утверждения:

1. Если при прямолинейном движении путь s, пройденный точкой, есть функция от времени t, т. е. s = f(t), то скорость точки есть производная от пути по времени, т. е. v(t) = f '(t).

Этот факт выражает механический смысл производной.

2. Если в точке х₀ к графику функции у = f(x) проведена касательная, то число f '(x₀) есть тангенс угла α между этой касательной и положительным направлением оси Ох, т. е. f '(x₀) = tg α. Этот угол называют углом наклона касательной.

Данный факт выражает геометрический смысл производной.

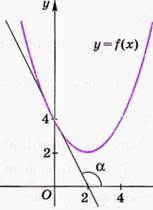ПРИМЕР 3. Найдем тангенс угла наклона касательной к графику функции у = 0,5х² – 2х + 4 в точке с абсциссой х = 0.

Найдем производную функции f(x) = 0,5х² – 2х + 4 в любой точке х, используя следующее равенство:

( a х² + b х + c )' = 2 ax + b

(0,5x² – 2x + 4)' = 0,5 ∙ 2 ∙ х – 2 = х – 2.

Вычислим значение этой производной в точке х = 0:

f '(0) = 0 – 2 = – 2.

Следовательно, tgα = – 2. График функции у = f(x) и касательная к ее графику в точке с абсциссой х = 0 изображены на рисунке.

Оздоровительные паузы в соответствии с ЗОЖ)

Выполнение пары несложных физических упражнение типа наклонов в разные стороны, встряхивание кистями рук.

7. Подведение итогов урока (результаты оценивания выставляются в журнал)  3^/

Обучающиеся отвечают на вопросы, что они сегодня изучили, что было понятно, а что нет.

8.  Домашнее задание (разъяснение домашнего задания)                                          2^/

Учебник математики под редакцией Башмакова – стр171-176;

Учебник математики под редакцией Никольского, 11 класс – §4.1, №4.8.

 

Преподаватель:______________     А.О. Тренихин

Председатель ПЦК: ______________ Л.Н. Хоменко

---

Дата добавления: 2022-01-22; просмотров: 14; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!