Примеры для самостоятельной работы
Лекция № 16
Нахождение оригинала по изображению функции
При отыскании оригинала по изображению функции в простейших случаях используют таблицу изображений основных элементарных функций и теоремы разложения (первую и вторую).
Первая теорема разложения. Если изображение искомой функции может быть разложено в степенной ряд по степеням 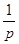 , т.е.
, т.е.
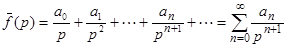
(этот ряд сходится к 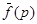 при | p| > R, где
при | p| > R, где 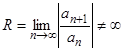 ), то оригинал f(t) находится по формуле
), то оригинал f(t) находится по формуле
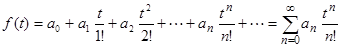 ,
,
причем этот ряд сходится для всех значений t.
Вторая теорема разложения позволяет найти оригинал для изображения, являющегося дробно-рациональной функцией от р, т.е. 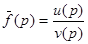 , где и(р) и v(р) – многочлены от р соответственно степени т и п, причем т < п.
, где и(р) и v(р) – многочлены от р соответственно степени т и п, причем т < п.
Если разложение v(р) на простейшие множители имеет вид
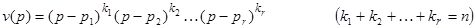 ,
,
то функцию 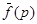 можно разложить на сумму элементарных дробей вида
можно разложить на сумму элементарных дробей вида 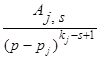 , где j принимает все значения от 1 до r, а s – все значения от 1 до kj. Таким образом,
, где j принимает все значения от 1 до r, а s – все значения от 1 до kj. Таким образом,
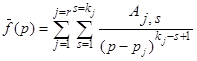 .
.
Все коэффициенты этого разложения можно определить по формуле
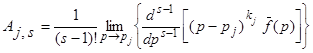 . (1)
. (1)
Вместо этой формулы для вычисления коэффициентов 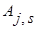 могут быть использованы элементарные приемы, применяемые в интегральном исчислении при интегрировании рациональных дробей. В частности, это целесообразно делать в тех случаях, когда все комплексные корни знаменателя v(р) простые и попарно сопряженные.
могут быть использованы элементарные приемы, применяемые в интегральном исчислении при интегрировании рациональных дробей. В частности, это целесообразно делать в тех случаях, когда все комплексные корни знаменателя v(р) простые и попарно сопряженные.
Если все корни v(р) простые, т.е.
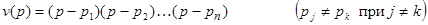 ,
,
то разложение упрощается:
|
|
|
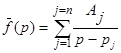 , где
, где 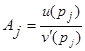 .
.
При отыскании тем или иным способом разложения 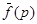 на простейшие дроби оригинал f(t) находится по следующим формулам:
на простейшие дроби оригинал f(t) находится по следующим формулам:
а) в случае кратных корней знаменателя v(р)
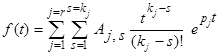 ; (2)
; (2)
б) в случае простых корней знаменателя v(р)
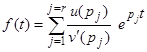 . (3)
. (3)
Эта теорема может быть обобщена на случай любой мероморфной функции (отношения двух целых трансцендентных функций). Примером мероморфной функции может служить th р – отношение целых функций sh p и ch p. При некоторых ограничениях, точную формулировку которых можно найти в курсах теории функции комплексного переменного,[1] мероморфная функция разлагается в ряд по простейшим дробям:
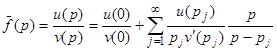 . (4)
. (4)
Здесь принято, что целая функция в знаменателе v(р) имеет только простые корни р1, р2, р3, …, причем у нее нет нулевого корня; предполагается далее, что вещественные части всех корней ограничены; иными словами, все полюсы 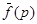 лежат слева от некоторой прямой, параллельной мнимой оси плоскости р. Впрочем, можно ограничиться требованием, чтобы справа от этой прямой лежало лишь конечное число полюсов
лежат слева от некоторой прямой, параллельной мнимой оси плоскости р. Впрочем, можно ограничиться требованием, чтобы справа от этой прямой лежало лишь конечное число полюсов 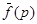 .
.
Оригинал, соответствующий изображению (4), будет
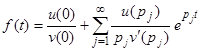 .
.
Пример 11. Найти оригинал функции 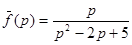 .
.
|
|
|
Используем элементарные приемы для разложения этой дроби на сумму таких дробей, оригиналы которых известны:
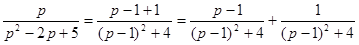 .
.
По формулам VI и VII таблицы имеем
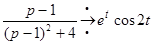 ;
; 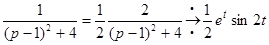 ,
,
поэтому 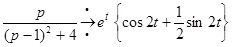 .
.
Пример 12. Найти оригинал функции 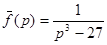 .
.
И в этом примере, используя элементарные приемы разложения, известные из интегрального исчисления, разложим данную дробь на простейшие:
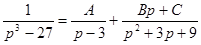 .
.
Для определения коэффициентов имеем тождество
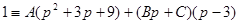 .
.
Полагая р = 3, находим 1 = 27 А; 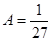 . Приравнивая коэффициенты при р2 нулю и свободный член – единице, получим А + В = 0, 9А – 3С = 1. Отсюда В = - А =
. Приравнивая коэффициенты при р2 нулю и свободный член – единице, получим А + В = 0, 9А – 3С = 1. Отсюда В = - А = 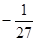 ; С =
; С = 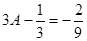 . Следовательно,
. Следовательно,
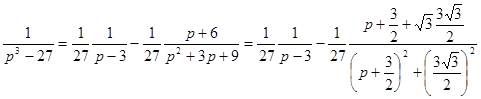 .
.
Таким образом,
 .
.
Отсюда, используя формулы III, VI, VII таблицы изображений, находим
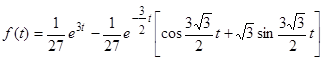 .
.
Пример 13. Найти оригинал функции 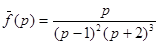 .
.
Разложение 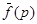 на простейшие дроби имеет вид
на простейшие дроби имеет вид
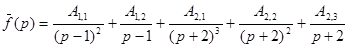 .
.
Находим коэффициенты этого разложения, используя формулу (1):
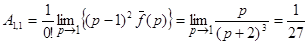 ;
;
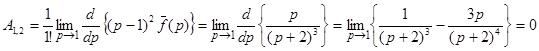 ;
;
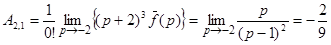 ;
;
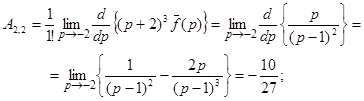
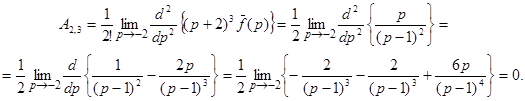
Таким образом,
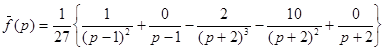 .
.
Отсюда, используя формулу VIII, находим
 .
.
Пример 14. Найти оригинал функции 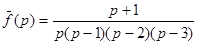 .
.
Поскольку в данном случае все корни знаменателя действительные и простые, лучше всего воспользоваться формулой (3). Имеем
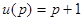 ,
, 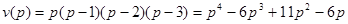 ;
;
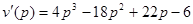 .
.
Находим корни v(p): р1 = 0; р2 = 1; р3 = 2; р4 = 3. Далее, получим
 ;
;  ;
; 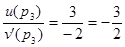 ;
; 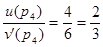 .
.
Отсюда по формуле (3) определяем
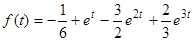 .
.
Пример 15. Найти оригинал 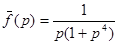 , используя первую теорему разложения.
, используя первую теорему разложения.
|
|
|
Имеем 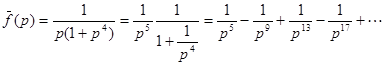 .
.
Этот ряд сходится при 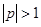 . Отсюда вычисляем
. Отсюда вычисляем
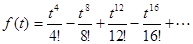 .
.
Примеры для самостоятельной работы
13. Найти f(t), если 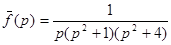 .
.
Найти оригиналы по данным изображениям:
14. 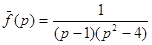 ; 15.
; 15. 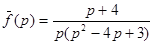 ;
;
16. 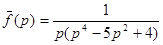 ; 17.
; 17. 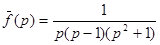 ;
;
18. 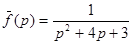 ; 19.
; 19. 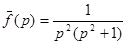 .
.
20. С помощью первой теоремы разложения найти оригинал для функции  , где k – целое положительное число.
, где k – целое положительное число.
21. С помощью первой теоремы разложения найти оригинал для функции 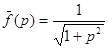 .
.
Общая формула обращения
Пусть функция f(t) обладает следующими свойствами:
1. f(t) º 0 при t < 0;
2. 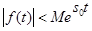 при t > 0, где М > 0 и s0 – некоторые действительные постоянные;
при t > 0, где М > 0 и s0 – некоторые действительные постоянные;
3. На любом конечном отрезке [a, b] положительной полуоси Ot функция f(t) удовлетворяет условиям Дирихле, т.е.: а) ограничена; б) либо непрерывна, либо имеет конечное число точек разрыва I рода; в) имеет конечное число экстремумов.
Тогда функция 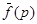 , определяемая равенством
, определяемая равенством 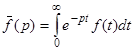 , является аналитической в полуплоскости Re p ³ s1 > s0. При этом справедлива формула обращения (формула Римана – Меллина)
, является аналитической в полуплоскости Re p ³ s1 > s0. При этом справедлива формула обращения (формула Римана – Меллина)
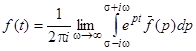 , или
, или 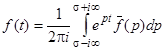 ,
,
дающая выражение оригинала f(t) через изображение 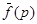 , причем s - произвольное число, удовлетворяющее неравенству s > s0.
, причем s - произвольное число, удовлетворяющее неравенству s > s0.
Если 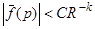 , где
, где 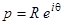 , -p < q < p, R > R0, R0, C, k > 0 – постоянные, то интеграл
, -p < q < p, R > R0, R0, C, k > 0 – постоянные, то интеграл 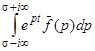 в формуле обращения может быть заменен на интеграл
в формуле обращения может быть заменен на интеграл 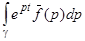 , где g - окружность с центром в начале координат, которая содержит внутри все полюса функции
, где g - окружность с центром в начале координат, которая содержит внутри все полюса функции 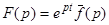 . Следовательно,
. Следовательно, 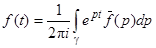 .
.
|
|
|
Применив основную теорему о вычетах, получаем
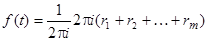 ,
,
где r1, r2, …, rm – вычеты функции F(p) относительно полюсов. Итак, 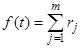 . Эта формула для дробно-рационального изображения в подробной записи есть не что иное, как формулы (2) и (3).
. Эта формула для дробно-рационального изображения в подробной записи есть не что иное, как формулы (2) и (3).
Пример 16. Найти оригинал по изображению 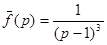 .
.
Находим вычет функции 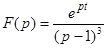 :
:
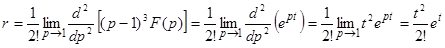 .
.
Следовательно, 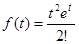 .
.
Пример 17. Найти оригинал по изображению
 .
.
Имеем 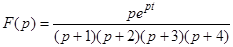 ;
;
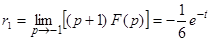 ;
; 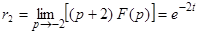 ;
;
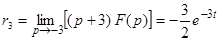 ;
; 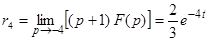 .
.
Следовательно, 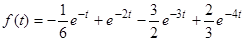 .
.
Дата добавления: 2022-01-22; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
