Условный пример расчета ранговой корреляции.

Уровень значимости

· Чем больше n, тем меньше максимальная ошибка . Однако, даже при заданном n нельзя абсолютно достоверно указать величину «треугольник», как как расчет этой величины, как и любой статистический вывод, делают на основе результатов эксперимента, а они заведомо содержат ошибки

· Выводы, которые делают на основе неточных данных, принципиально не могут быть абсолютно достоверными. Поэтому говорят о надежности статистического вывода, которую оценивают величиной доверительной вероятности p, где 0 < p < 1.

· Например, статистический вывод, сделанный с доверительной вероятностью p = 0.95, будет справедлив в 95 случаях из 100. Будем пользоваться чаще величиной q = 1-p, называемой уровнем значимости.

· Уровень значимости задается заранее, до проведения расчетов. Типичные значения для q: 0.01, 0.05; и 0.1 или в процентах 1,5,10.

 

Определение грубых наблюдений

· Грубые наблюдения (промахи) подлежат исключению из выборки.

· Для их обнаружения можно вновь воспользоваться t – критерием Стьюдента.

· В этом случае сомнительный результат y_i , временно исключают из выборки, а по ставшимся данным рассчитывают средн ее арифметическое y_ср и дисперисию.

· Далее вычисляют величину t_расч:

· Из таблиц распределения Стьюдента, по выбранному уровню значимости и числу степеней свободы, связанному с дисперсией, находят табличное значение t – критерия t_табл. Если t_расч > t_табл, то подозреваемый результат является промахом и должен быть исключен и выборки.

~y – y среднее

y_макс - ~y =

~y – y_min =      max = y_i

 

Проверка нормальности распределения случайных величин

· При рассмотрении предыдущих статистических процедур предполагалось, что выходная величина подчиняется нормальному закону распределения.

· Это предположение можно проверить разыми способами. Наиболее строгим из них является применение критерия x­_­­­² Пирсона.

· Для этого необходимо иметь выборку достаточно большого объема :  Диапазон измерения выходной величины в этой выборке разбивается на I интервалов так, чтобы эти интервалы покрывали всю ось от  и в каждый интервал при этом попало не менее пяти значений выходной величины.

· Подсичтывают количество наблюдений, попавших в каждый интервал. Затем вычисляют теориетические вероятности попадани я случайной величины в каждый I интервал

· Для этого используют формулу p_i = Ф(z₂) – Ф(z₁)

 

Проверка нормальности распределения случайных величин

Следующим этапом является вычисление величины X_расч²_:

 

 

Гипотезу о нормальности распределения можно принять, если X²­_расч < X²­_табл. Расчет сводится в таблицу.

Проверка статистических гипотез

· Результаты экспериментальных исследований часто используют, например для сравнения условий функционирования объектов, оценки сравнительной эффективности различных технологий, разных способов измерения и т.д. Во многих случаях соответствующие выводы делают на основе анализа и сравнения нескольких выорок. Одна из простых задач такого типа возникает , когда надо сравнивать точность двух измерительных приборов.

· Пусть имеются две выборки объемом n₁ и n₂, по которым найдены выборочные дисперсии s²₁ и s²₂ . Требуется выяснить, можно ли утверждать, что обе выборки взяты из одной и той же генеральной совокупностью.

 

1. Проверка однородности двух дисперсий

· Для проверки статистической гипотезы об однородности двух дисперсий используется критерий Фишера F.

· 1. Вначале вычисляется величина F_расч , равная отношению большей из выборочных дисперсий к меньшей

· 2. Далее задаются уровнем значимости q и вычисляют числа степенй свободы дисперсий числителя и знаменателя по формулам: f₁ = n₁ – 1 и f₂=n₂ – 1.

· 3. По трём величинам q, f₁ и f₂  из таблиц распределения Фишера (таблица) отыскивают величину F = F_табл.

· 4. Если F_расч > F_табл, то выборочные дисперсии считаются неоднородными (различие между ними значимо) для выбранного уровня значимости q. Если F_расч <= F_табл, то можно принять гипотезу об однородности дисперсий.

2. Проверка однородности нескольих дисперсий по выборкам одинакового объема.

Для проверки однородности нескольких дисперсий при равных объемах всех рассматриваемых выборок n₁=n₂=n₃=…=n может быть использовать G – критерий Кохрена.

Пусть m – число выборочных дисперсий, однородность которых проверяется. Обозначим эти дисперсии .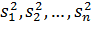

Вычисляется расчетное G – отношение по формуле:

В числителе этой формулы стоит наибольшая из расматриваемых дисперсий, а в знаменателе – сумма всех дисперсий.

3. Далее обращаются к таблицам распределения Кохрена. По выбранному уровню значимости, числу степеней свободы каждой выборки и по количеству выборок из этой таблицы отыскивают величину G = G_расч. Если G_расч < G_табл ……. Жопа

3. Проверка однородности нескольких дисперсий по выборкам разного объема.

· Экспериментаторы часто планируют получение выборок одинакового объема, однако, если в опытах обнаруживаются промахи, то после их исключения объемы выборок оказываются различными.

Критерий Бартлетта.

Из таблиц при уровне значимости и числе степеней свободы k = m-1 отыскивают значение X_табл². Гипотеза об однородности дисперсий принимается, если B<= X²_табл.

4. Проверка однородности средних значений

· При проверке однородности средних значений исследуются две выборки, имеющие различные средние арифметические.

· Данная проверка позволяет установить, вызвано или расхождение между средними случайными ошибками измерения или оно связано с влиянием каких-либо неслучайных факторов.

· Проверка проводится с применением t – критерием Стьюдента.

· Пусть n₁ и n₂ – объемы выборок , y_1ср и y­_2ср – соответствующие средние, s²₁  и s²₁ – оценки дисперсий , найденных по этим выборкам.

 

Коэффициент корреляции

· Во многих случаях целью экспериментальных исследований является установление и изучение зависимости между некоторыми величинами. Если каждая из этих величин является случайной, то при этом используют методы корреляционного анализа.

· Будем говорить, что между двумя случайными величинами имеется статистическая связь, если при изменении одной из них меняется распределение другой.

· Для оценки статистической связи по данным эксперимента широко используется выборочный коэффициент корреляции.

· Пусть проведено n наблюденний и в каждом из них определялись значения двух параметров (признаков) x и y. Следовательно, имеются две одновременно получаемые выборки: x₁, x₂, …, x­_n и y₁, y₂, …, y_n.

· По каждой из их найдём среднее арифметическое и дисперсии. Выборочный коэффициент корреляции рассчитывается по формуле:

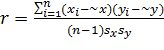
· Коэффициент корреляции всегда лежит в пределах

· Он характеризует не всякую, а только линейную зависимость между случайными величинами.

· При положительном r можно предполагать, что с возрастанием одной из случайных величин другая в среднем тоже возрастает. При отрицательном r с ростом одной из них другая величина будет в среднем убывать.

· Чем ближе величина r к (+1) или (-1), тем больше степень линейной зависимости между рассматриваемыми случайными величинами.

 

· Значение r, равное нулю, свидетельствует об отсутствии линейной статистической связи меду ними.

· Такие случайные величины называют некоррелированными.

· Обычно величина оказывается на равной нулю

· Для выяснения того, будут ли некоррелированными в этом случае признаки x и y, вычисляют величину

· Её сравнивают с табличным значением t – критерия Стьюдента, найденным при выбранном уровне значимости q и числе степеней свободы f = n-2

· Если 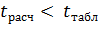, принимается гипотеза о некоррелированности величин x и y. В противном случае коэффициент корреляции значимо отличается от нуля, т.е между величинами x и y  существует линейная статическая связь.

· Если требуется исследовать статистическую связь между тремя и более случайными величинами, то пользуются коэффициентом множественной корреляции.

· Так, для оценки степени статистической связи случайной величины z с величинами x и y рассчитывают выборочный совокупный коэффициент корреляции p по формуле:

· Где r­_xy, r_yz, r_xz – коэффициеты корреляции соответственн между величинами x и y, y и z, x и z.

· Величина p лежи в пределах 0 <= p <= 1

 

· Иногда требуется установить наличие взаимосвязи между двумя качественными признаками, т.е признаками, которые не являются численно измеримыми.

· Исследуемые объекты в этом случае можно поранжировать, т.е. пронумеровать в порядке возрастания или убывания признака. Этот номер, присвоенный объекту, называется рангом.

· Так как исследуются два признака то каждому i-му объекту присваивается два ранга: x_i и y_i в соответствии с признаками x и y. Таким образом, имеем две последовательности рангов:

· По признаку x: x­₁, …, x_n;

· По признаку y: y₁, y₂, …, y_n.

· Одним из способов оценки связи меду двумя качественными признаками является вычисление коэффициента ранговой корреляции Спирмена.

· Формула имеет вид:

·

 

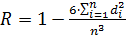
Коэффициент ранговой корреляции Спирмена

· Этот коэффициент измеряется в пределах от -1 о +1, а его абсолютная величина пропорциональна степени зависимости между признаками х и у.

· Оценка значимости коэффициента проводится точно так же, как и для обычного коэффициента корреляции.

· Эта проверка корректна в данном случае при n>= 9

Условный пример расчета ранговой корреляции.

· Требуется выяснить, имеется ли взаимосвязь между уровнем специализации предприятия по номенклатуре продукции (единый конструктив или технология) и себестоимостью продукции. Допустим, что для каждого предприятия был рассчитан совокупный показатель специализации, учитывающий номенклатуру выпускаемой продукции, а так же их объемы.

· Ранжирование по уровню специализации:

[1 2 3 4 5 6 7 8 9 10]

· Ранжирование по себестоимости

· [8 6 9 10 7 3 4 2 1 5]

· В первой строке предприятия пронумерованы в порядке возрастания специализации, т.е большему номеру соответствует более высокий уровень специализации.

· Далее для каждого предприятия была вычислена себестоимость производства единицы продукции (шт, т.).

· В соответствии с этой величиной каждому предприятию был присвоен ранг, причем большему значению себестомости соответствует больший ранг.

· Вычислим коэффициент ранговой корреляции спирмена по формуле:

·

·

· Для оценки значимости найденного значения вычисляем величину t_расч

· t_{расч =}2,93

· t_табл = 2.31 (при уровне значимости q = 0.05 и числе степеней свободы n равной 10-2 = 8)

· t_расч>t_табл => ранговая корреляция между уровнем специализации предприятия и себестомостью продукции существует.

 

Использование коэффициента конкордации для обработки экспертных оценок при ранжировании.

· Коэффициент конкордации характеризует степень согласованности мнений экспертов. Признаками в данном случае служат мнения экспертов.

· Согласованность мнений экспертов важна при прогнозировании и планировании экспериментов.

· Пусть имеется n факторов x₁, x₂, …, x_n влияющих на функционирование объекта.

· Требуется выявить важнейшее из этих факторов, чтобы подвергнуть их дальнейшему исследованию.

· Каждому из m экспертов предлагается список факторов с указанием диапазона их варьирования.

· Эксперта просят приписать ранги этим факторам – пронумеровать их в порядке убывания степени их влияния на объект.

· Результаты сводятся в таблицу. Здесь a_ij – ранг, приписанный j – м экспертом i-му фактору.

 

Коэффициент конкордации рассчитывается по формуле:

· Величина может принимать значения в пределах 0 <= W <= 1. Чем ближе к 1 значение W, тем больше согласие между экспертами. Для оценки значимости коэффициента конкордации используется .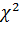

· Вычисляется:

Которое сравнивается с величиной  найденной при уровне значимости и числе степенй свободы f = n-1

· Если 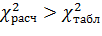 то фиксируется согласие экспертов при данном уровне значимости

 

---

Дата добавления: 2022-01-22; просмотров: 28; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!