Фазовый портрет свободных затухающих колебаний.
Лекция 6. «Колебания» (продолжение).
Свободные затухающие колебания. Декремент и логарифмический декремент колебаний.
Вынужденные колебания. Установившиеся вынужденные колебания. Механический резонанс.
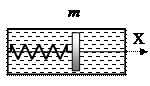Рассмотрим движение тела в вязкой среде под действием квазиупругой силы вблизи положения равновесия (например, поршня на невесомой пружине). Будем считать, что сила сопротивления пропорциональна скорости тела: 
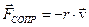, где r – коэффициент сопротивления (Н×с/м). Уравнение движения поршня в проекции на ось X можно записать в виде: 
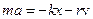или
,
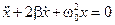где введены обозначения: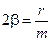 
, 
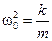. Это уравнение называется уравнением свободных затухающих колебаний.Если r = 0, то получаем уравнение свободных незатухающих колебаний: 
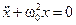с периодом 
.
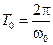Полная механическая энергия системы равна сумме кинетической и потенциальной энергий:
.
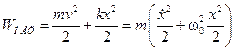Для затухающих колебаний механическая энергия не остаётся постоянной:
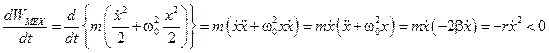, а убывает.
Решение уравнения свободных затухающих колебаний ищем в виде: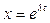 
. Подставим в уравнение и, после сокращений, получаем характеристическое уравнение:
.
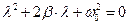Дискриминант квадратного уравнения: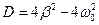 
,
значения корней: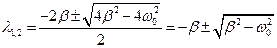 
.
Тогда решение уравнения должно иметь вид:
,
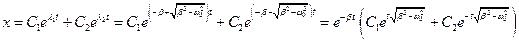где С1 и С2 – постоянные коэффициенты.
|
|
|
Воспользуемся формулой Эйлера: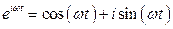 
, где 
.
При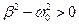 
решение не описывает колебания.
Колебания будут наблюдаться, если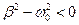 
. Введем обозначение: 
.
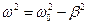Тогда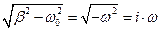 
и решение уравнения примет вид:
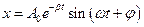
- оно описывает свободные колебания циклической частоты w, затухающие с течением времени. Циклическая частота затухающих колебаний: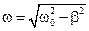 
, период: 
.
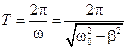Необходимым условием колебательного движения является неравенство: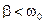 
.
Величина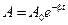 
является амплитудой затухающих колебаний. С течением времени амплитуда убывает – говорят, что колебания затухают. Временем затухания (временем релаксации) называется время, за которое амплитуда убывает в е раз:
, 
, 
.
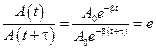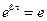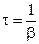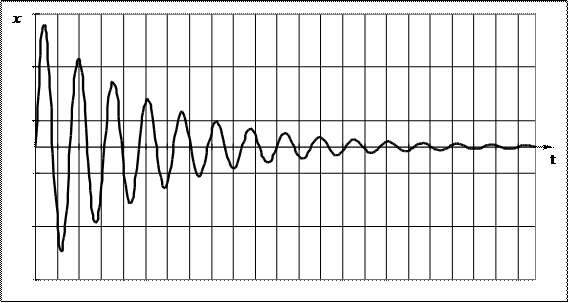
Число полных колебаний, совершаемое системой за это время: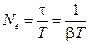 
.
Декремент затухания – отношение амплитуд колебаний через период:
.
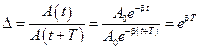Логарифмический декремент затухания: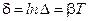 
. Поэтому 
.
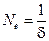Величина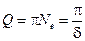 
называется добротностью колебательной системы.
Энергию колебаний в момент времени t можно определить как: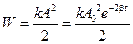 
.
Убыль энергии за один период: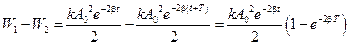 
.
Рассмотрим отношение запасённой энергии к убыли энергии за один период колебаний: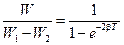 
.
|
|
|
При малом логарифмическом декременте затухания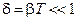 
воспользуемся разложением:
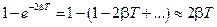. Учитывая, что 
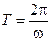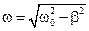, и при малых b, можно считать 
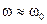, тогда получаем:
.
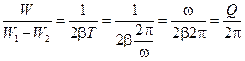Для затухающих свободных колебаний добротность характеризует скорость убывания энергии при малых затуханиях.
Фазовый портрет свободных затухающих колебаний.
Пусть задан закон колебательного движения: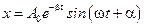 
.
Тогда скорость при колебаниях:
.
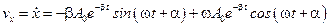Импульс: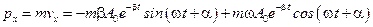 
.
Так как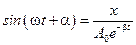 
и 
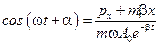, то
.
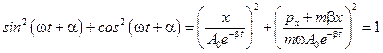Фазовая траектория представляет собой сужающуюся к нулевой точке спираль. Вращение происходит по часовой стрелке (т.к. с течением времени значения x и px стремятся к нулю).
Вынужденные колебания.
Рассмотрим движение тела в вязкой среде вблизи положения равновесия под действием квазиупругой силы и некоторой периодической силы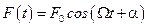 
.
Второй закон Ньютона: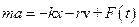 
перепишем в виде:
,
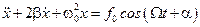где введены обозначения: , ,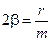 
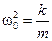. Это уравнение называется уравнением вынужденных колебаний.
Решением этого обыкновенного дифференциального уравнения является сумма решений однородного и частного решения неоднородного уравнений.
|
|
|
Однородное уравнение:
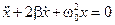
является уравнением свободных затухающих колебаний.
Частное решение неоднородного уравнения
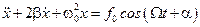
будем искать в виде: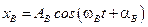 
. Изобразим это уравнение на амплитудно-векторной диаграмме, на которой величине 
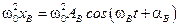соответствует вектор 
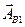, такой что 
.
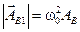Так как величина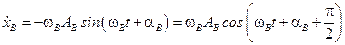 
, то величине 
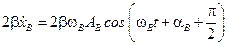соответствует вектор 
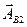, повернутый относительно вектора 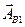на угол 
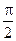, длина которого 
.
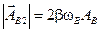Величине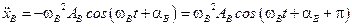 
соответствует вектор 
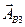, повернутый на угол p относительно вектора 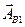и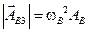 
.
В правой части уравнения величине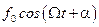 
соответствует вектор 
.
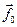Уравнению 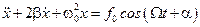будет соответствовать векторная сумма:
.
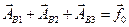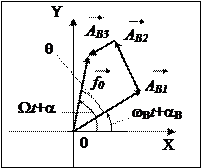Так как длины векторов не меняются, то это равенство возможно только для случая, когда: 
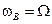. Таким образом, вынужденные колебания происходят с частотой вынуждающей силы.
Из диаграммы следует, что при этом должно выполняться равенство: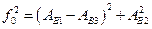 
, поэтому получаем:
.
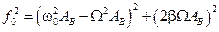Откуда находим амплитуду вынужденных колебаний:
.
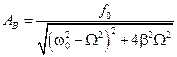Обозначим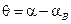 
- разность фаз вынуждающей силы и вынужденных колебаний.
|
|
|
Из диаграммы следует, что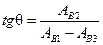 
, т.е. 
.
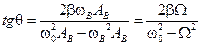Таким образом, при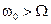 
получаем, что q >0 – вынужденные колебания отстают по фазе от вынуждающей силы, а при 
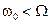- вынужденные колебания опережают по фазе вынуждающую силу.
Следствие. Под действием периодической силы тело совершает два вида колебаний - свободные затухающие колебания с собственной частотой w, и вынужденные – с частотой вынуждающей силы W. Затухающие колебания с течением времени прекратятся и останутся только вынужденные колебания – их называют установившимися.
Дата добавления: 2022-01-22; просмотров: 55; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!