Решатели дифференциальных уравнений в MATLAB

Лекция №8

Обыкновенные дифференциальные уравнения

Постановка задачи Коши

Обыкновенные дифференциальные уравнения занимают видное место в науке, в особенности в ее естественнонаучных областях. Они широко используются в механике при расчете различного рода движений, в других разделах физики, например, при расчетах электрических цепей, в химической кинетике при анализе баланса реагентов, в популяционной биологии (модели типа хищник-жертва), в экономике, в политике и во множестве других приложений. Ряд важных задач математической физике, описываемых на языке уравнений в частных производных допускают в ряде случаев сведения к системам обыкновенных дифференциальных уравнений (например, автомодельные решения). В общем и целом обыкновенные дифференциальные уравнения являются одним из самых востребованных инструментов описания и расчета самых разнообразных явлений и процессов в науке, технике и обществоведении.

Конкретная прикладная задача может сводиться к решению произвольного дифференциального уравнения произвольного порядка либо к произвольной системе дифференциальных уравнений. При этом известно, что произвольное дифференциальное уравнений p-го порядка

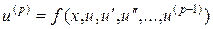(1)

при помощи замены можно свести к системе p уравнений первого порядка:

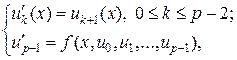(2)

где . Используя алгоритм перехода от (1) к (2), можно любую систему любого порядка свести к системе уравнений первого порядка. Поэтому в дальнейшем будем в основном работать с системой уравнений первого порядка следующего вида:

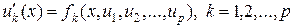, (3)

которую также будем записывать в сокращенной, векторной форме

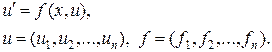(3¢)

Известно, что система уравнений (3), (3¢) имеет множество решений, которые в общем случае зависят от p параметров c = (c₁,…,c_p), что можно записать в виде: u = u(x,c). Для выделения единственного решения необходимо наложить p дополнительных условий.

Различают три типа задач для систем дифференциальных уравнений:

· задачи Коши;

· краевые задачи;

· задачи на собственные значения.

Задача Коши или задача с начальными данными предполагает дополнительные условия вида:

, (4)

т.е. в точке x₀ задаются значения всех функций системы уравнений (3). Условие (4) можно истолковать как задание начальной точки искомой интегральной кривой в p+1-мерном пространстве 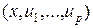. Решение системы уравнений (3) обычно требуется найти на отрезке [x₀,X] (либо на отрезке [X,x₀]).

Из курса дифференциальных уравнений известно, что, если правые части системы (3) непрерывны и удовлетворяют условию Липшица по переменным u_k, k = 1,…,n, то решение задачи Коши (3), (4) единственно и непрерывно зависит от координат начальной точки, т.е. задача корректно поставлена. Если правые части имеют непрерывные производные по всем аргументам до q-го порядка, то решение u = u(x) имеют производные вплоть до порядка q +1.

Методы решения дифференциальных уравнений можно классифицировать на точные, приближенные и численные.

Точные методы позволяют выразить решения дифференциальных уравнений либо через элементарные функции, либо с помощью квадратур от элементарных функций. Точные методы решения уравнений (3), (4) изучаются в курсе обыкновенных дифференциальных уравнений.

На листинге_№1 приведен код программы, иллюстрирующий использование специальной функции dsolve в MATLAB, которая точно решает обыкновенные дифференциальные уравнения произвольного порядка.

Листинг_№1

%примеры аналитического решения обыкновенных

%дифференциальных уравнений с помощью функции

%MATLAB - dsolve

%пример №1 (u'=au)

expl1=dsolve('Du=a*u','x')

%пример №2 (u'=u^2)

expl2=dsolve('Du=u^2','x')

%пример №3 (u''-g=0)

expl3=dsolve('D2u-g=0','x')

%пример №4 (u''+q^2u=0)

expl4=dsolve('D2u+q^2*u=0','x')

%пример №5 (u''-(3/4)x^(-2)u=0)

expl5=dsolve('D2u-(3/4)*x^(-2)*u=0','x')

%пример №6 (u'=f(x))

expl6=dsolve('Du=f(x)','x')

%пример №7 (u'=(u-x)/(u+x))

expl7=dsolve('Du=(u-x)/(u+x)','x')

После запуска на исполнение кода программы листинга_№1, получим следующую информацию:

expl1 =

C1*exp(a*x)

expl2 =

-1/(x-C1)

expl3 =

1/2*g*x^2+C1*x+C2

expl4 =

C1*sin(q*x)+C2*cos(q*x)

expl5 =

C1/x^(1/2)+C2*x^(3/2)

expl6 =

Int(f(x),x)+C1

Warning: Explicit solution could not be found; implicit solution returned.

> In dsolve at 310

In ode_anal at 17

expl7 =

-1/2*log((x^2+u^2)/x^2)-atan(u/x)-log(x)-C1 = 0

Согласно информации представленной выше, MATLAB решил все семь дифференциальных уравнений, при этом последнее уравнение он не смог разрешить относительно зависимой переменной u, о чем и доложил.

Приближенными будем называть методы, в которых решение u(x) получается как предел некоторой последовательности u_n(x), при этом u_n(x) выражаются либо в аналитическом виде с помощью элементарных функций, либо с помощью квадратур от элементарных функций.

Численные методы представляют собой алгоритмы вычисления приближенных значений искомой функции u(x) в узлах некоторой сетки значений аргумента x₁,…,x_n. Основным недостатком численных методов является то, что они позволяют найти частное решение, например решение задачи Коши, но не общее решение u = u(x,c) уравнения (3). Этот недостаток компенсируется тем, что численные методы универсальны и могут быть использованы для решения широкого класса дифференциальных уравнений.

Численные методы могут быть использованы только для задач, решение которых существует и единственно, т.е. если задача корректно поставлена. Однако условие корректности необходимо, но не достаточно для численного решения задачи. Необходимо еще, чтобы задача была хорошо обусловлена, т.е. малые шевеления в начальных (входных) данных приводили к малым изменениям в решениях. Если это условие не выполнено, но считается, что задача плохо обусловлена (слабо устойчива), т.е. небольшие погрешности входных данных или метода могут сильно исказить решение.

Приведем простой пример плохо обусловленной задачи. Необходимо численно найти решение следующей задачи:

. (5)

Задача (5) имеет точное общее решение: 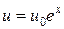и частное u º 0, входным значением для задачи является параметр u₀. Плохая обусловленность задачи (5) выражается в том, что, если пошевелить входной параметр u₀, например, сделать его равным не ноль, а 10^-⁶, то решение в точке 100 сильно изменится, т.е. u(100) = 2,688×10³⁷.

Метод Пикара

Данный метод решает задачу Коши. Для простоты записи ограничимся одним дифференциальным уравнением. Алгоритм легко обобщается на случай системы дифференциальных уравнений путем формальной замены u(x) и f(x,u) на соответствующие векторы. Метод Пикара является приближенным методом, обобщающим метод последовательных приближений.

Рассмотрим задачу Коши для уравнения первого порядка

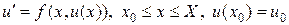. (6)

Интегрируя дифференциальное уравнение (6), заменим исходную задачу эквивалентной ей задачей решения интегрального уравнения Вольтерра.

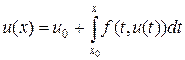. (7)

Решая интегральное уравнение (7) методом последовательных приближений, получим итерационный процесс Пикара

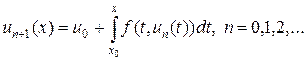(8)

На каждом этапе итерационного процесса Пикара в (8) интегрирование выполняется либо точно, либо численными методами, разобранными в лекции №4.

Доказательство сходимости метода Пикара предполагает, что в некоторой ограниченной области G(x,u) правая часть уравнения (6) — f(x,u) непрерывна и удовлетворяет по переменной u условию Липшица, т.е.

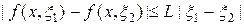Поскольку область G(x,u) ограничена, постольку выполняются неравенства: 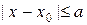, 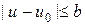. Введем обозначения для погрешности приближенного решения: z_n(x) = u_n(x) - u(x). Вычитая (7) из (8) и используя условие Липшица, находим

. (9)

Решая последовательно рекуррентное соотношение (9), находим

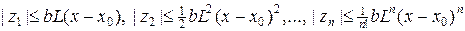Из последних неравенств следует оценка погрешности

. (10)

Из оценки погрешности в (10) следует, что 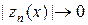при n ® ¥, т.е. приближенное решение равномерно сходится к точному во всей области G(x,u).

Для иллюстрации метода Пикара применим его к решению уравнения вида:

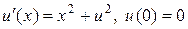. (11)

На листинге_№2 приведен код программы, которая рассчитывает последовательные приближенные решения уравнения (11) методом Пикара.

Листинг_№2

%Программа расчета последовательных

%приближений методом Пикара для решения

%уравнения u'(x)=x^2+u^2, u(0)=0

%очищаем рабочее пространство

clear all

%задаем максимальное число

%последовательных приближений

nmax=4;

%определяем символические переменные

syms x0 u0 x

x0=0; u0=0; u=u0;

%задаем цикл последовательных приближений Пикара

for n=1:nmax

u=u0+int(x^2+u^2,x0,x)

end

Ниже приведен итог работы кода программы листинга_№2 в виде четырех последовательных приближений к решению уравнения (11). Видно, что при |x| £ 1 приближения быстро сходятся к истинному решению с высокой точностью.

u =

1/3*x^3

u =

1/3*x^3+1/63*x^7

u =

1/59535*x^15+2/2079*x^11+1/63*x^7+1/3*x^3

u =

1/109876902975*x^31+4/3341878155*x^27+
662/10438212015*x^23+82/37328445*x^19+
13/218295*x^15+ 2/2079*x^11 +1/63*x^7+1/3*x^3

Метод малого параметра

Метод малого параметра был предложен А.Пуанкаре в 1892г. Пусть правая часть уравнения (6) зависит от параметра l, т.е.

, (12)

при этом известно некоторое частное решение u₀(x) при некотором значении параметра l = l₀. Решение будем искать в виде ряда

. (13)

Подставим (13) в (12) и проведем разложение в ряд Тейлора по степеням (l - l₀). Объединим слагаемые с сомножителями одной и той же степени по (l - l₀) и приравняем их к нулю, тогда

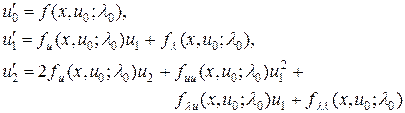(14)

и т.д. Общий член разложения (14) можно представить в виде

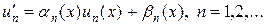(15)

т.е. определение коэффициентов разложения (13) сводится к решению линейных уравнений (15).

Рассмотрим пример. Пусть f(x,u;l) = x² + (1 + l)u² и l₀ = -1. На листинге_№3 приведен код программы, которая аналитически решает уравнения (14) для нашего примера.

Листинг_№3

%Программа позволяющая аналитически решать

%дифференциальное уравнение u'=f(x,u,L) методом

%малого параметра до второго порядка

%очищаем рабочее пространство

clear all

%определяем символические переменные

syms x u u0 u1 L L0

%определяем значение параметра, в окрестности

%которого решение раскладывается в ряд Тейлора

L0=-1;

%определяем правую часть дифференциального уравнения

f=x^2+(1+L)*u^2;

f0=compose(f,L0,L,L);

f0=compose(f0,u0,u,u0);

%находим нулевое приближение

u0=dsolve(['Du0=' char(f0)],'u0(0)=0','x')

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

duf=diff(f,u);

duf0=compose(duf,L0,L,L);

duf0=compose(duf0,u0,u,x);

dLf=diff(f,L);

dLf0=compose(dLf,L0,L,L);

dLf0=compose(dLf0,u0,u,x);

%находим первое приближение

u1=dsolve(['Du1=' char(duf0) '*u1+' char(dLf0)],...

'u1(0)=0','x')

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

d2uf=diff(f,u,2);

d2uf0=compose(d2uf,L0,L,L);

d2uf0=compose(d2uf0,u0,u,x);

d2Luf=diff(dLf,u);

d2Luf0=compose(d2Luf,L0,L,L);

d2Luf0=compose(d2Luf0,u0,u,x);

d2Lf=diff(f,L,2);

d2Lf0=compose(d2Lf,L0,L,L);

d2Lf0=compose(d2Lf0,u0,u,x);

alph2=2*duf0;

bet2=d2uf0*u1^2+d2Luf0*u1+d2Lf0;

%находим второе приближение

u2=dsolve(['Du2=' char(alph2) '*u2+' char(bet2)],...

'u2(0)=0','x')

Итог работы программы листинга_№3 приведен ниже в виде аналитических выражений для приближений u₀(x), u₁(x), u₂(x) соответственно.

u0 =

1/3*x^3

u1 =

1/63*x^7

u2 =

2/2079*x^11

Метод ломаных

Рассмотрим задачу Коши (6) и выберем на отрезке [x₀,X] некоторую, вообще говоря, неравномерную сетку x₀ < x₁ < … < x_N = X. Разложим решение u(x) в ряд Тейлора на отрезке [x_n,x_n ₊₁] в окрестности x_n, тогда

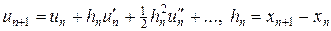, (16)

где 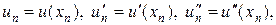n = 0,1,…,N - 1.

Производные, входящие в (16) могут быть найдены путем дифференцирования уравнения (6), т.е.

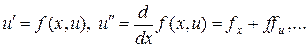(17)

Схема решения дифференциального уравнения (16), (17) однако мало употребительна, т.к. вычисления высших производных согласно (17) может оказаться затруднительным, а если правая часть известна с какой либо погрешностью, то результат и вовсе не определен.

В простейшей схеме ломаных в (16) оставляют только член с первой производной, а остальные отбрасывают, т.е. рассматривается следующая схема приближенного решения дифференциального уравнения:

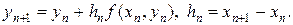(18)

В (18) приближенное решение дифференциального уравнения (6) в точке x_n обозначено символом y_n в отличие от точного значения u_n = u(x_n). Согласно схеме ломаных, задавая начальное значение y₀ = u₀, находим по формуле (18) y₁, y₂ и т.д. y_N. Отметим, что схему ломаных часто также называют схемой Эйлера.

На рис.1 приведена геометрическая интерпретация метода ломаных. Приближенное решение из точки (x_n,y_n) движется по касательной к интегральной кривой, в точке (x_n ₊₁,y_n ₊₁) решение движется по новой касательной к новой интегральной кривой и т.д. В результате получается ломаная линия, изображающая приближенное решение исходного уравнения.

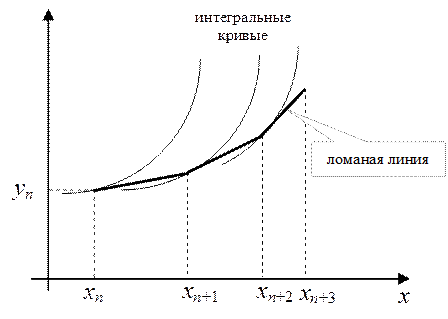
Рис.1. Геометрическая интерпретация метода ломаных

Для исследования сходимости метода ломаных предположим наличие непрерывности и ограниченности правой части f(x,u) и ее первых производных, т.е. 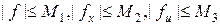, а согласно (17) .

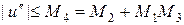Определим погрешность приближенного решения метода ломаных z_n = y_n - u_n. Вычитая уравнение (17) из (18), находим

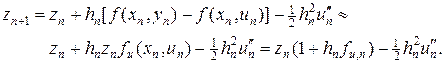(19)

Рекурсивная зависимость (19) позволяет выразить погрешность на каждом шаге через погрешность начальных данных:

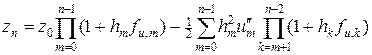. (20)

При малых значениях шагов сетки произведения, входящие в (20), могут быть без потери точности переписаны в виде:

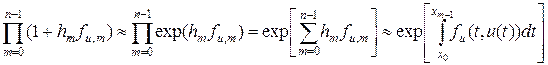С учетом вышеуказанного представления, уравнение (20) может быть представлено в виде:

, (21)

где h(t) — некоторая непрерывная функция, равная h_n в узлах x_n. Если начальное условие выбрано точно, то погрешность начального данного z₀ = y₀ - u₀ отсутствует, т.е. z₀ = 0. Проводя далее оценку погрешности в (21), находим

, (22)

где

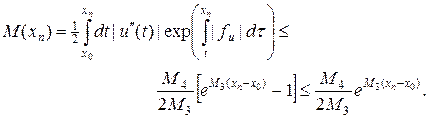(22¢)

Согласно (22), погрешность стремится к нулю при 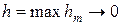, т.е. методом ломаных действительно можно получить приближенную оценку решения дифференциального уравнения (6), при этом численное решение равномерно сходится к точному решению с первым порядком точности по h. Хотя оценка величины M(x_n) в (22¢) является мажорантной, т.е. завышенной, наличие экспоненты в данной оценке говорит о том, что решение по схеме Эйлера может оказаться плохо обусловленным алгоритмом.

Изучим поведение оценки погрешности (22), (22¢) на примере численного решения уравнения вида:

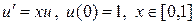. (23)

Уравнение (23) имеет точное решение , которое сравним с приближенным решением y_n, которое определим на равномерной сетке x_n = (n - 1)h, n = 1,…,N, где шаг сетки h = 1/(N - 1). Изучим зависимость величины константы (22¢)

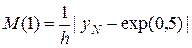(24)

от шага сетки. Согласно теоретическим оценкам величина M(1) не должна зависеть от величины шага h при h ® 0.

На листинге_№4 приведен код программы вычисления зависимости величины (24) от шага сетки.

Листинг_№4

%Программа изучения погрешности численного

%решения дифференциального уравнения

%u'=f(x,u) методом Эйлера (методом ломаных)

%очищаем рабочее пространство

clear all

%задаем набор сеток расчета уравнения u'=xu

Mesh=10:10:10000;

%организуем цикл расчета методом ломаных

%на разных сетках

for k=1:length(Mesh)

%определяем параметры сетки

N=Mesh(k); h=1.0/(N-1);

%задаем начальное условие

y(1)=1;

%применяем алгоритм метода ломаных

for n=1:(N-1)

y(n+1)=y(n)+(n-1)*h^2*y(n);

end

%вычисляем величину M(1) в оценке

%погрешности численного решения

M(k)=abs(y(N)-exp(0.5))/h;

step(k)=h;

end

%рисуем зависимость величины M(1) от шага

%разностной сетки (при изображении зависимости

%необходимо перейти в логарифмический масштаб

%по оси абсцисс)

plot(step,M);

На рис.2 приведен итоговый график зависимости. Видно, что при стремлении шага сетки к нулю действительно величина M(1) ведет себя как константа.

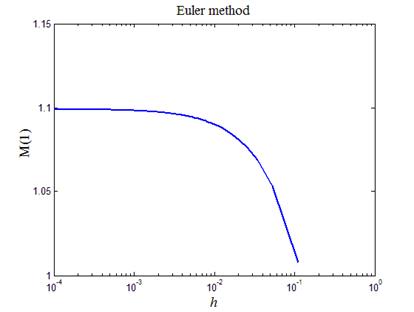
Рис.2. Изучение погрешности метода ломаных

Метод Рунге-Кутта

Метод Рунге-Кутта позволяет строить схемы различного порядка точности. Эти схемы наиболее востребованы в практике из-за своей простоты и надежности.

Разберем алгоритм Рунге-Кутта на примере построения схемы второго порядка точности. Если обратиться к разложению в ряд Тейлора (16), то для вычисления u_n₊₁ со вторым порядком точности нам необходимо знать вторую производную 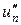. Чтобы не вычислять вторую производную, ее можно представить в виде конечной разности, т.е. 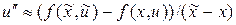. Это наводящее соображение позволяет предложить следующую схему численного решения дифференциального уравнения:

, (25)

где, как и выше, y_n — численное решение исходного уравнения (6), a, b, g, d — некоторые параметры, которые определяются ниже.

Разложим второе слагаемое в квадратных скобках в (25) в ряд Тейлора по шагу сетки h, тогда

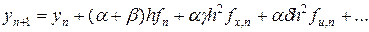(26)

Комбинируя (16), (17), находим

(26¢)

Подберем теперь параметры a, b, g, d так, чтобы выражение (26) совпало с (26¢) в пределах разложения Тейлора до второй степени по шагу сетки h. Это требование реализуется, когда

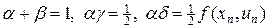. (27)

Выражая все параметры согласно (27) через a и подставляя полученные выражения в (25), получим однопараметрическое семейство двухчленных схем Рунге-Кутта

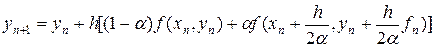, (28)

где a берется из полуинтервала (0,1].

Погрешность схемы (28) может быть оценена также, как и в схеме ломаных. Результат оценок следующий. Если правая часть f(x,u) ограничена и непрерывна вместе со вторыми производными, то численное решение, полученное по схеме (28), равномерно сходится к точному решению с погрешностью , т.е. сходимость осуществляется со вторым порядком точности. Проверим это.

На листинге_№5 приведен код решения дифференциального уравнения из предыдущего пункта (23). Здесь также как и в предыдущем листинге нас интересует поведение константы 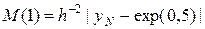в зависимости от шага сетки h.

Листинге_№5

%Программа иллюстрирующая решение

%дифференциального уравнения методом

%Рунге-Кутта второго порядка точности

%очищаем рабочее пространство

clear all

%задаем значение параметра, определяющего

%семейство схем Рунге-Кутта

alpha=0.25;

%задаем правую часть дифференциального

%уравнения u'=f(x,u)

f=@(x,u)x*u;

%задаем набор сеток

Mesh=10:50:10000;

%организуем цикл расчетов с разными сетками

for k=1:length(Mesh)

N=Mesh(k); h=1.0/(N-1);

%задаем начальное условие

y(1)=1;

%вычисляем приближенные значения решения

%дифференциального уравнения

for n=1:(N-1)

x(n)=(n-1)*h;

y(n+1)=y(n)+h*((1-alpha)*f(x(n),y(n))+...

alpha*f(x(n)+h/(2*alpha),y(n)+...

(h/(2*alpha))*f(x(n),y(n))));

end

%находим константу M в оценке погрешности

%приближенного решения |y(N)-u(N)|<=Mh^2,

%она не должна зависеть от h

M(k)=abs(y(N)-exp(0.5))/h^2;

step(k)=h;

end

%рисуем зависимость константы M от шага сетки h

%(по оси абсцисс переходим к логарифмической

%системе координат средствами MATLAB)

plot(step,M);

На рис.3 приведен итоговый график зависимости константы M(1) от шага сетки (при a = 0,25). Видно, что, начиная с некоторого, при меньших значениях шага величина M(1) действительно не зависит от параметра h. В частности этот график подтверждает квадратичную оценку сходимости семейства схем Рунге-Кутта (28). Кроме того, был исследован также вопрос численной применимости метода Рунге-Кутта со значениями параметра a вне полуинтервала (0,1]. Оказалось, что и при этих значениях метод Рунге-Кутта по схеме (28) может быть использован.

Рассмотрим геометрическую интерпретацию схем Рунге-Кутта для двух значений параметра a = 1 и 0,5. В первом случае, подставляя a = 1, в (28), находим

. (29)

Вводя половинные значения аргумента x_n _+1/2 и функции y_n _+1/2, схему (29) можно переписать в следующем виде

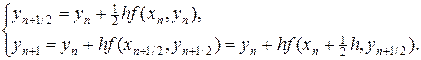(30)

Геометрическая интерпретация схемы (30) представлена на рис.4,а. Согласно первому шагу в схеме (30), методом ломаных находится значение решения в половинном точке отрезка [x_n,x_n₊₁], далее вычисляется производная решения в половинной точке и в этом направлении делается шаг на всем отрезке [x_n,x_n₊₁].

Рис.3. Изучение погрешности семейства схем метода
Рунге-Кутта (28)

Во втором случае при a =0,5 имеем следующую схему:

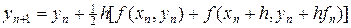. (31)

Для геометрической интерпретации схемы (31) перепишем ее в следующем виде:

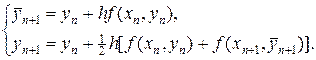(32)

Согласно первому шагу в схеме (32), находим предварительное значение решения 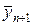, на втором шаге оно уточняется путем коррекции правой части как полусуммы правой части в точке x_n и предварительного решения 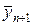. Геометрическая интерпретация данной процедура приведена на рис.4,б.

Схемы численного расчета дифференциальных уравнений типа (30), (32) называют часто также как схемы “предиктор — корректор”.


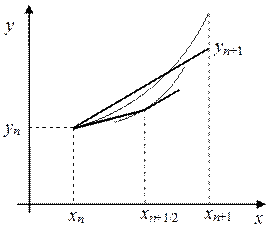
Рис.4,а. Геометрическая интерпретация схемы Рунге-Кутта (30)	Рис.4,б. Геометрическая интерпретация схемы Рунге-Кутта (32)

Рассмотрим одну схемы третьего порядка точности. Одна из них без вывода представлена ниже.

(33)

Протестируем схему (33) на предмет выяснения порядка точности. Для этого, как и в предыдущих двух программах будем численно решать уравнение (23) на отрезке [0,1], сравнивая численное решение и точное, при этом ошибка не должна превышать величину . Нас будет интересовать поведение константы 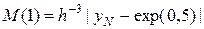в зависимости от шага сетки h. Код соответствующей программы приведен на листинге_№6.

Листинг_№6

%Программа иллюстрирующая решение

%дифференциального уравнения методом

%Рунге-Кутта третьего порядка точности

%очищаем рабочее пространство

clear all

%задаем правую часть дифференциального

%уравнения u'=f(x,u)

f=@(x,u)x*u;

%задаем набор сеток

Mesh=10:50:10000;

%организуем цикл расчетов с разными сетками

for k=1:length(Mesh)

N=Mesh(k); h=1.0/(N-1);

%задаем начальное условие

y(1)=1;

%вычисляем приближенные решения

%дифференциального уравнения

for n=1:(N-1)

x(n)=(n-1)*h;

k1=f(x(n),y(n));

k2=f(x(n)+0.5*h,y(n)+0.5*h*k1);

k3=f(x(n)+h,y(n)+h*(-k1+2*k2));

y(n+1)=y(n)+(h/6)*(k1+4*k2+k3);

end

%находим константу M в оценке погрешности

%приближенного решения |y(N)-u(N)|<=Mh^3,

%она не должна зависеть от h

M(k)=abs(y(N)-exp(0.5))/h^3;

step(k)=h;

end

%рисуем зависимость константы M от шага сетки h

%(в графическом окне MATLAB по оси абсцисс

%переходим в логарифмическую систему координат)

plot(step,M);

На рис.5,а приведен итоговый график зависимости величины M(1) от шага сетки. Видно, что где-то между значениями 10^-⁴ и 10^-³ шага сетки величина M(1) становится нестабильной и колеблется в небольшом диапазоне. В конечном счете, эти колебания связаны с тем, что данная схеме повышенной точности начинает “чувствовать” ограниченность мантиссы чисел типа double в MATLAB. В следующем примере схемы Рунге-Кутта еще более высокого — четвертого порядка точности, колебания величины M(1) перейдут в экспоненциальный рост.


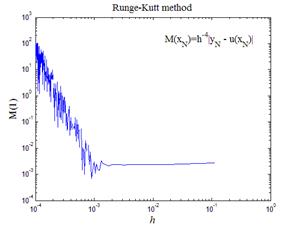
Рис.5,а. Изучение погрешности метода Рунге-Кутта третьего порядка (33)	Рис.5,б. Изучение погрешности метода Рунге-Кутта четвертого порядка (34)

Наиболее употребительны схемы четвертого порядка точности. Одна из них без вывода представлена ниже.

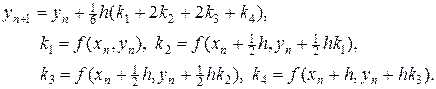(34)

Протестируем схему (34) на предмет выяснения порядка точности. Для этого, как и в предыдущих трех программах будем численно решать уравнение (23) на отрезке [0,1], сравнивая численное решение и точное, при этом ошибка не должна превышать величину . Нас будет интересовать поведение константы в зависимости от шага сетки h. Код соответствующей программы приведен на листинге_№7.

Листинг_№7

%Программа иллюстрирующая решение

%дифференциального уравнения методом

%Рунге-Кутта четвертого порядка точности

%очищаем рабочее пространство

clear all

%задаем правую часть дифференциального

%уравнения u'=f(x,u)

f=@(x,u)x*u;

%задаем набор сеток

Mesh=10:50:10000;

%организуем цикл расчетов с разными сетками

for k=1:length(Mesh)

N=Mesh(k); h=1.0/(N-1);

%задаем начальное условие

y(1)=1;

%вычисляем приближенные решения

%дифференциального уравнения

for n=1:(N-1)

x(n)=(n-1)*h;

k1=f(x(n),y(n));

k2=f(x(n)+0.5*h,y(n)+0.5*h*k1);

k3=f(x(n)+0.5*h,y(n)+0.5*h*k2);

k4=f(x(n)+h,y(n)+h*k3);

y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);

end

%находим константу M в оценке погрешности

%приближенного решения |y(N)-u(N)|<=Mh^4,

%она не должна зависеть от h

M(k)=abs(y(N)-exp(0.5))/h^4;

step(k)=h;

end

%рисуем зависимость константы M от шага сетки h

%(в графическом окне MATLAB по осям абсцисс и

%ординат переходим в логарифмическую систему

%координат)

plot(step,M);

На рис.5,б приведена итоговая зависимость величины M(1) от шага сетки. Видно, что при шаге сетки меньше 10^-³ величины M(1) быстро возрастает. Этот рост можно объяснить тем, что в силу высокой точности схемы дальнейшее уменьшении шага нецелесообразно, т.к. мантисса чисел с плавающей запятой типа double в MATLAB ограничена приблизительно 15-ю значащими цифрами.

Схемы Рунге-Кутта имеют следующий ряд преимуществ, которые делают их одними из самых популярных:

· схемы Рунге-Кутта (кроме схемы ломаных) имеют высокую точность;

· они являются явными, т.е. значение решения на следующем уровне вычисляется по вполне определенным формулам от предыдущих значений;

· все схемы Рунге-Кутта допускают расчет с переменным шагом сетки, это делает их еще более гибкими при использовании в приложениях;

· для расчета достаточно задать лишь начальное значение, дальнейшие значения искомой функции получаются путем расчета по одним и тем же формулам.

Методы Рунге-Кутта легко обобщаются для решения систем дифференциальных уравнений путем формальной замены u и f на 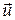и 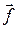. Так схема Рунге-Кутта четвертого порядка точности для системы дифференциальных уравнений 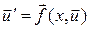приобретает следующий вид:

(35)

Схему Рунге-Кутта (35) проиллюстрируем на примере решения системы уравнений описывающей колебания линейного маятника, т.е. численно решим пару дифференциальных уравнений вида:

на отрезке [0,p /4] при начальных данных 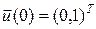. Эта задача имеет единственное решение 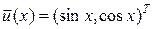. Нас будет интересовать численное решение в точке x = p /4. Точное значение вектора-функции в этой точке равно . Сравним точное значение с приближенным при различных значениях шага сетки, т.е. вычислим величину

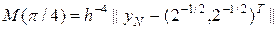, (36)

где || || — некоторая векторная норма. Эта величина для схемы (35) должна выходить на некоторую константу при h ® 0. При этом для погрешности схемы (35) можно дать оценку .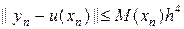

Для выяснения зависимости величины (36) от шага сетки была написана программа, код которой приведен на листинге_№8.

Листинг_№8

%Программа иллюстрирующая решение системы

%дифференциальных уравнений методом

%Рунге-Кутта четвертого порядка точности

%очищаем рабочее пространство

clear all

%задаем правую часть дифференциального

%уравнения u'=f(x,u)

f=@(x,u)[u(2);-u(1)];

Mesh=10:50:10000;

%организуем цикл расчетов с разными сетками

for k=1:length(Mesh)

N=Mesh(k); h=(0.25*pi)/(N-1);

%задаем начальное условие

y(:,1)=[0;1];

%вычисляем приближенные решения системы

%дифференциальных уравнений

for n=1:(N-1)

x(n)=(n-1)*h;

k1=f(x(n),y(:,n));

k2=f(x(n)+0.5*h,y(:,n)+0.5*h*k1);

k3=f(x(n)+0.5*h,y(:,n)+0.5*h*k2);

k4=f(x(n)+h,y(:,n)+h*k3);

y(:,n+1)=y(:,n)+(h/6)*(k1+2*k2+2*k3+k4);

end

%находим константу M в оценке погрешности

%приближенного решения |y(N)-u(N)|<=Mh^4,

%она не должна зависеть от h

M(k)=norm(y(:,N)-[1;1]/sqrt(2))/h^4;

step(k)=h;

end

%рисуем зависимость константы M от шага сетки h

%(в графическом окне MATLAB по осям абсцисс и

%ординат переходим в логарифмическую систему

%координат)

plot(step,M);

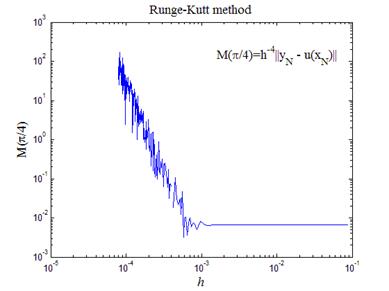
Рис.6. Изучение погрешности метода Рунге-Кутта
четвертого порядка для системы уравнений

На рис.6 приведен итоговый график зависимости. Его можно сравнить с графиком на рис.5,б. Оба графика показывают сходные зависимости; при шаге сетки меньше 10^-³ величина M(p /4) начинает быстро расти. Причина роста аналогична той, которая обсуждались выше в связи с ограниченностью мантиссы чисел типа double в MATLAB.

Метод Адамса

Пусть в точках сетки …,x_n_-₃, x_n_-₂, x_n_-₁, x_n известны приближенные решения …,y_n_-₃, y_n_-₂, y_n_-₁, y_n дифференциального уравнения u¢ = f(x,u), тогда известны также значения правой части дифференциального уравнения в точках сетки, т.е. F(x_k) = f(x_k,y_k), k = …,n-3, n-2, n-1, n. Наличие значений правой части позволяет аппроксимировать ее интерполяционным полиномом. Запишем интерполяционный полином в форме Ньютона

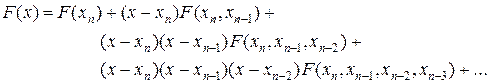(37)

Ограничимся в дальнейшем лишь теми членами в (37), которые представлены до символа троеточия. Данные члены уже обеспечивают четвертой порядок точности.

Для вычисления значения решения в следующей точке x_n₊₁, запишем исходное дифференциальное уравнение в интегральной форме:

. (38)

Подставим в (38) интерполяционный полином (37), тогда, после соответствующего интегрирования, получим схему Адамса переменного шага

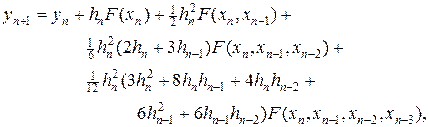(39)

где 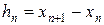. Если в (39) отбросить последнее слагаемое, то схема будет иметь третий порядок точности, если два последних, то схема будет иметь второй порядок и т.д.

Часто схема Адамса используется на равномерной сетке. В этом случае вместо разделенных разностей, входящих в формулу Ньютона (37), привлекают конечные разности 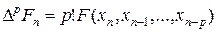. С учетом последней формулы схему Адамса (39) на равномерной сетке можно представить в виде:

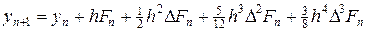. (40)

Чтобы начать расчет по схеме Адамса (39) или (40) надо знать не только начальное значение y(x₀), но также значения в точках x₁, x₂, x₃. Эти дополнительные значения необходимо найти каким-либо иным методом, например, Рунге-Кутта. Привлекательным свойством метода Адамса является то, что в отличие, например, от методов Рунге-Кутта, значение функции f(x,u) вычисляется один раз на одном шаге. Это может оказаться важным для случая, когда вычисление функции f(x,u) довольно трудоемко.

Протестируем метод Адамса на примере решения уравнения u¢ = xu на отрезке [0,1], где в качестве начального значения выбирается u(0) = 1. Решение данной задачи известно: u(x) = exp(0.5x²). Нас будет интересовать точность численной оценки в точке x_N = 1, где 0 = x₀ < x₁ < … < x_N = 1 — некоторая равномерная сетка на отрезке [0,1]. В силу построения схемы Адамса, точность численной оценки решения должна удовлетворять соотношению , т.е. величина M(1) не должна зависеть от h при h ® 0. Проверим это, построив зависимость величины от шага сетки. На листинге_№9 приведен соответствующий код программы, которая осуществляет численное решение дифференциального уравнения методом Адамса.

Листинг_№9

%Программа решения дифференциального уравнения

%методом Адамса

%очищаем рабочее пространство

clear all

%определяем правую часть дифференциального

%уравнения u'=f(x,u)

f=@(x,u)x*u;

%определяем набор сеток

Mesh=10:50:10000;

%организуем цикл расчета методом Адамса для

%различных сеток

for k=1:length(Mesh)

N=Mesh(k); h=1.0/(N-1);

%определяем начальное данное

y(1)=1;

%находим методом Рунге-Кутта четвертого

%порядка значения функции в трех последующих

%точках, т.е. в точках x(2), x(3), x(4)

for n=1:3

x(n)=(n-1)*h;

k1=f(x(n),y(n));

k2=f(x(n)+0.5*h,y(n)+0.5*h*k1);

k3=f(x(n)+0.5*h,y(n)+0.5*h*k2);

k4=f(x(n)+h,y(n)+h*k3);

y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);

x(n+1)=x(n)+h;

end

%вычисляем значения правой части в первых четырех

%точках сетки

for n=1:4

F(n)=f(x(n),y(n));

end

%организуем вычисления последующих значений искомой

%функции методом Адамса

for n=4:(N-1)

y(n+1)=y(n)+h*F(n)+0.5*h*(F(n)-F(n-1))+...

(5.0/12)*h*(F(n)-2*F(n-1)+F(n-2))+...

(3.0/8)*h*(F(n)-3*F(n-1)+3*F(n-2)-F(n-3));

x(n+1)=x(n)+h;

F(n+1)=f(x(n+1),y(n+1));

end

%находим константу M в оценке погрешности

%приближенного решения |y(N)-u(x(N))|<=Mh^4,

%она не должна зависеть от h

M(k)=abs(y(N)-exp(0.5))/h^4;

step(k)=h;

end

%рисуем зависимость константы M от шага сетки h

%(в графическом окне MATLAB по осям абсцисс и

%ординат переходим в логарифмическую систему

%координат)

plot(step,M);

Рис.7. Изучение погрешности метода Адамса

На рис.7 приведен итоговый график работы кода программы листинга_№9. На этом графике изображена зависимость константы M(1) от шага сетки. Как и для метода Рунге-Кутта четвертого порядка, при шаге сетки меньше 10^-³ величина M(1) начинает быстро расти, что обусловлено ограниченность мантиссы чисел типа double в MATLAB приблизительно 15-ю значащими цифрами. Есть еще одна особенность метода Адамса по сравнению с методом Рунге-Кутта. Если сравнить рис.5,б и рис.7, то обнаруживается, что константа M(1) в методе Адамса в 10³ раз больше соответствующей константы в методе Рунге-Кутта той же точности.

Решатели дифференциальных уравнений в MATLAB

В пакете MATLAB существует несколько так называемых решателей системы обыкновенных дифференциальных уравнений: ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb и некоторые другие. Аббревиатура ode означает ordinary differential equations, а суффикс s (s — stiff) обозначает то, что метод применим к решению жестких систем дифференциальных уравнений (о понятии “жесткость” будем говорить далее).

Решатель ode23 представляет метод Рунге-Кутты порядка 2-3, модифицированный Богацки и Шампиной; решатель ode45 — метод Рунге-Кутты порядка 4-5, модифицированный Дормандом и Принцем; решатель ode113 представляет метод Адамса, Башворта и Моултона.

В связи с разбором других решателей дифференциальных уравнений рассмотрим неявные схемы численного решения дифференциальных уравнений. До сих пор использовались явные схемы вычислений, когда значение функции на следующем уровне вычислялось по известным формулам от предыдущих значений искомой функции.

Простейший вариант неявной схемы Эйлера имеет следующий вид:

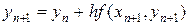. (41)

Чтобы найти численное решение y_n ₊₁на следующем слое, необходимо решить уравнение (41) относительно y_n ₊₁. Это можно осуществить несколькими способами. Например, с помощью метода итераций

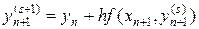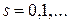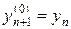, ; . (42)

Условием сходимости метода итераций (42) является условие h||f_u|| < 1. Возможно также разложить в (41) функцию 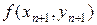в ряд Тейлора по 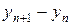, тогда

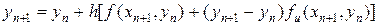. (43)

Разрешая (43) относительно y_n ₊₁, получаем значение решения на следующем уровне. Такой метод приближенного решения уравнения (41) называется методом Розенброка.

Используется также еще один неявный метод, основанный на формуле трапеции:

. (44)

Функция ode23t использует неявный метод трапеций типа (44) с использование “свободной” интерполяции. Эту функцию рекомендуется использовать для умерено жестких задач, когда требуется высокоточное решение. Функция ode23tb использует неявный метод Рунге-Кутты на первом шаге по методу трапеций, а на втором шаге методом “дифференцирования назад” второго порядка. Подобно ode23s данная функция может оказаться более эффективной, чем ode15s, если не требуется высокая точность.

Куртис и Хиршфельдер в 1952г. ввели понятие жестких задач и предложили для их решения неявные методы “дифференцирования назад”. Одна из таких схем второго порядка имеет следующий вид:

. (45)

Определение жесткости системы дифференциальных уравнений дадим в соответствии с учебником^{^[1]}.

Пусть дана система дифференциальных уравнений вида:

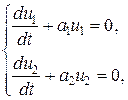(46)

где t > 0, a₁, a₂= const>0. Решение системы уравнений (46) имеет следующий вид:

Пусть a₂>> a₁, тогда, при достаточно большом t , в векторе решений 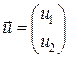остается компонента u₁, а u₂ ® 0.

Рассмотрим простейшую разностную схему Эйлера для решения системы уравнений (46):

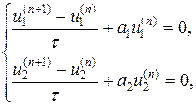(47)

где t — шаг по времени t, , t_n = n t, n =0,1,…, i =1,2. Схема Эйлера (47) устойчива, когда t a₁£ 2, t a₂£ 2, т.е. при

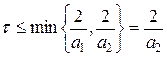. (48)

Согласно формуле (48), шаг интегрирования системы дифференциальных уравнений с помощью явных разностных схем ограничен характерным временем наиболее медленного процесса. В системе (46) два характерных времени: 1/ a₁ и 1/ a₂. Поскольку a₂>> a₁, постольку верна формула (48).

Введем определение жесткости. Пусть дана система обыкновенных дифференциальных уравнений:

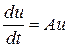. (49)

Система дифференциальных уравнений (49) с постоянной матрицей A(m ´ m) называется жесткой, если собственные значения l _k, k =1,2,…, m матрицы A удовлетворяют следующим условиям:

1) Rel _k < 0, k =1,2,…, m, т.е. система асимптотически устойчива по Ляпунову;

2) отношение 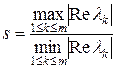велико.

Число s называется числом жесткости системы (49). В пакете MATLAB число жесткости возвращает функция cond.

Общий способ решения жестких систем дифференциальных уравнений был найден на пути применения неявных абсолютно устойчивых разностных методов. Например, систему (46) можно решить с помощью неявного метода Эйлера:

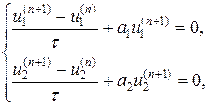который устойчив при всех t > 0.

Для прояснения природы жесткости, рассмотрим пример решения уравнения Ван Дер Поля. Уравнение Ван-Дер-Поля описывает релаксационные колебания в электронных устройствах. Это уравнение является жестким. Покажем это. Уравнение Ван-Дер-Поля 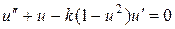перепишем в векторной форме, т.е.

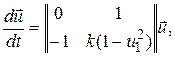(50)

где 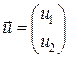, u₁= u, u₂= u¢. Величину 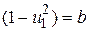можно считать порядка единицы, т.е. |b| ~ 1. Находя собственные значения матрицы в (50) при k >>1, имеем l₁= bk, l₂=1/ bk. В итоге число жесткости s = l₁/ l₂= b²k². Выбирая k =1000, находим s ~ 10⁶.

Решим нелинейную систему уравнений (50) с помощью схемы Куртиса-Хильшфельдера (45) и с помощью встроенного в MATLAB решателя ode23s. Код программы решения системы уравнений (50) представлен на листинге_№10.

Листинг_№10

%Программа иллюстрирующая решение жесткой

%системы дифференциальных уравнений на примере

%уравнения Ван Дер Поля

function vdp

global k

%численное решение уравнения Ван Дер Поля

%согласно схеме (45)

%определяем значение константы k и начальные

%данные для решения

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

k=10; h=0.01; t=0:h:100; y(:,1)=[0;1];

y(:,2)=y(:,1)+h*func(h,y(:,1)+...

0.5*h*func(h,y(:,1)));

%основной цикл расчета по схеме (45)

for n=2:(length(t)-1)

y(:,n+1)=(4*y(:,n)-y(:,n-1)+...

2*h*func((n-1)*h,y(:,n-1)))/3;

end

plot(t,y(1,:),t,y(2,:));

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%решение уравнения Ван Дер Поля с помощью

%решателя ode23s

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% k=1000;

% [T Y]=ode23s(@func,[0 5000],[0 1]);

% plot(T,Y(:,1),T,Y(:,2),...

% T(1:(length(T)-1)),diff(T));

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function y=func(x,u)

global k

y=[u(2);-u(1)+k*(1-u(1)^2)*u(2)];


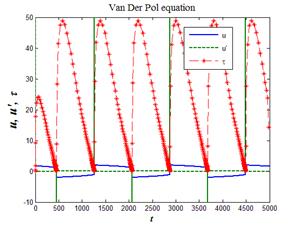
Рис.8,а. Численное решение уравнения Ван Дер Поля по схеме (45) при k =10	Рис.8,б. Численное решение уравнения Ван Дер Поля решателем ode23s при k =1000

Итог численного решения уравнения Ван Дер Поля согласно схеме (45) представлен на рис.8,а. С помощью данной схемы не удалось решить уравнение со значением параметра k = 1000, а только при k = 10, т.к. в этом случае требуется шаг интегрирования сделать недопустимо малым. В решателе ode23s эта проблема решается путем автоматического регулирования шага интегрирования. Итог решения уравнения Ван Дер Поля данным решателем представлен на рис.8,б. Помимо решения u, производной решения u¢, нанесен также график зависимости шага интегрирования t от аргумента — времени t. Видно, что шаг сильно уменьшается в окрестности точек с максимальной производной и, наоборот, вне этих точек шаг может значительно увеличиться.

Постановка краевой задачи

Краевая задача состоит в поиске частных решений системы уравнений (3), (3¢), т.е. системы

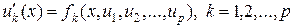, (51)

на отрезке [a,b], при задании дополнительных условий в более чем одной точке отрезка [a,b]. В рамках данного определения постановка краевой задачи возможна только для систем, порядок которых два и более.

Свое название краевые задачи получили вследствие задания условий на краях отрезка [a,b], т.е. в точках x = a и x = b. В качестве примера можно привести задачу определения статического прогиба u(x) струны с закрепленными концами под действием распределенной нагрузки f(x), которая поделена на длину и упругость струны:

. (52)

В общем случае краевая задача для системы (51) предполагает определенными p точек x₁, x₂, …, x _p на отрезке [a,b], в которых заданы условия вида:

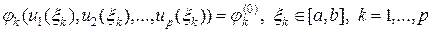. (53)

Точное решение краевой задачи (51), (53) в элементарных функциях удается редко, т.к. для этого надо найти общее решение системы (51), а затем определить конкретные значения констант, обеспечивающих выполнение краевых условий (53). По этой причине широко используются приближенные методы решения краевых задач. К ним относятся: метод стрельбы, разностный метод, метод разложения в ряды Фурье, методы Ритца и Галеркина.

В общем случае метод стрельбы состоит в сведении краевой задачи к задаче Коши и последующих итерациях, цель которых состоит в удовлетворении части граничных условий с заданной точностью. Разностный метод состоит в сведении исходной задачи к алгебраической системе уравнений большого порядка, в которой неизвестными выступают значения искомого решения в узлах сетки.

Метод стрельбы

Данный метод еще называют баллистическим. В основе этого метода лежит способ сведения краевой задачи к решению задачи Коши той же системы дифференциальных уравнений. Рассмотрим более подробно метод стрельбы на примере пары дифференциальных уравнений следующего вида:

(54)

где xÎ[a,b] и выбираются краевые условия общего вида:

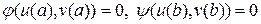. (55)

Выберем произвольное u_a такое, что u(a) = u_a. Подставим это условие в левое граничное условие, рассматривая его в качестве алгебраического уравнения, т.е. j(u_a,v(a)) = 0. Формально разрешим последнее уравнение относительно v(a), тогда v(a) = q(u_a). Решим теперь систему (54) как задачу Коши с начальными данными u(a) = u_a и v(a) = q(u_a). Решение можем провести одним из численных методов, изложенных выше. В итоге получим решение u(x,u_a), v(x,u_a), зависящие от u_a, как от параметра.

Функция q такова, что левое граничное условие выполнено. Однако выполнение правого граничного условия не обеспечено. Действительно, подставляя решение в правое граничное условие, получим

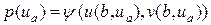(56)

функцию параметра u_a, которая отлична от нуля. Для обеспечения правого граничного условия надо осуществить варьирование параметра u_a так, чтобы с заданной точностью обеспечить равенство 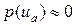. Другими словами, решение краевой задачи сводится к нахождению корней уравнения

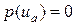. (57)

Методы поиска корней уравнения изучались в лекции №5. Например, можно численно решить систему уравнений (54) для различных значений u_a и найти среди них такую пару 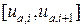, на которой функция p меняет знак. Далее к отрезку 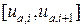применяем метод деления отрезка пополам, осуществляем каждый раз новую “пристрелку” параметра и добиваясь нужной точности значения корня. Вследствие такой процедуры метод получил название метода стрельбы.

Ранее мы уже видели, что метод дихотомии надежен и прост, однако он довольно медленный. Каждая итерация в данном случае особенно дорогая, т.к. предполагает решение системы уравнений (54). Построим аналог процесса Ньютона, предполагая нужную степень гладкости правых частей системы (54) и краевых условий (55).

Найдем производную функции (56)

. (58)

В уравнение (58) входят производные по параметру от решений системы уравнений (54). Введем обозначения

и продифференцируем систему уравнений (54) по параметру u_a, тогда

(59)

Одно из начальных значений для системы (59) легко найти, учитывая что u(a) = u_a, тогда 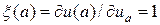. Второе граничное условие получается после дифференцирования левого граничного условия (55) по параметру u_a, тогда

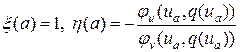. (60)

В результате решение краевой задачи свелось к решению системы четырех уравнений (54), (59) с начальными данными (55), (60). Решая данную систему уравнений, находим u(b), v(b), x(b), h(b). Подставляя эти величины в (58), находим производную, которая позволяет организовать процесс Ньютона для нахождения корня уравнения (57), т.е.

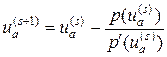. (61)

Добавление лишней пары дифференциальных уравнений (59) можно избежать, если воспользоваться в место процесса Ньютона (61) методом секущих

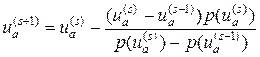. (62)

Изучим метод стрельбы на примере решения краевой задачи (54) — (61) в следующем уравнении:

, (63)

где e > 0 — некоторый неотрицательный параметр. При e = 0 решение задачи (63) известно u = sin(x). Переходя к представлению уравнения (63) в виде системы, а также повторяя логику вывода уравнений (59), находим

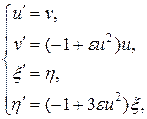(64)

где

;

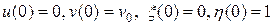. (65)

Итерационный процесс Ньютона для краевой задачи (64), (65) осуществляет пристрелку значения параметра v₀ таким образом, чтобы обеспечить выполнение правого краевого условия. Соответствующий итерационный процесс Ньютона имеет следующий вид:

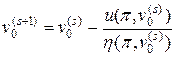. (66)

Краевая задача (63) — (66) решалась численно при различных значениях e. На листинге_№11 приведен код решения краевой задачи.

Листинг_№11

%Программа решения краевой задачи (63) - (66)

%очищаем рабочее пространство

clear all

%задаем возможные значения параметра eps

eps=0:2:10;

%определяем число точек на отрезке

%интегрирования [0,pi/2]

N=100;

%определяем правую часть системы дифференциальных

%уравнений (64)

f=@(z,e)[z(2);(-1+e*z(1)^2)*z(1);

z(4);(-1+3*e*z(1)^2)*z(3)];

%определяем шаг сетки h

h=(0.5*pi)/(N-1);

%организуем цикл решения краевой задачи для

%различных значений параметра eps

for k=1:length(eps)

iter=0;

v0=1.4; v1=0.7;

while (abs(v1-v0)>1e-4)&(iter<20)

v0=v1;

y(1,1)=0; y(2,1)=v0; y(3,1)=0; y(4,1)=1;

for n=1:(N-1)

%для интегрирования системы уравнений

%(64) применяем схему Рунге-Кутта 4-го

%порядка

k1=f(y(:,n),eps(k));

k2=f(y(:,n)+0.5*h*k1,eps(k));

k3=f(y(:,n)+0.5*h*k2,eps(k));

k4=f(y(:,n)+h*k3,eps(k));

y(:,n+1)=y(:,n)+(h/6)*(k1+2*k2+2*k3+k4);

end

%организуем итерации по Ньютону

v1=v0-(y(1,N)-1)/y(3,N);

iter=iter+1;

end

hold on

%строим графики решений при

%различных значениях eps

plot(0:h:0.5*pi,y(1,:));

end

На рис.9 приведены искомые решения краевой задачи, которые генерирует код программы листинга_№11, для 6 значений e = 0, 2, 4, 6, 8, 10.

Дата добавления: 2022-01-22; просмотров: 65; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!