Метод обратных итераций для поиска собственных векторов

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Метод обратных итераций предназначен для поиска собственного вектора x_i, когда соответствующее собственное значение l _i известно с некоторой погрешностью. Обозначим через 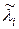возмущенное собственное значение, тогда, поскольку 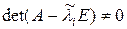, постольку уравнение 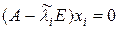имеет в качестве решения тривиальное, т.е. x_i = 0.

Возьмем произвольный вектор b и рассмотрим систему:

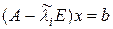. (20)

Определитель системы (20) отличен от нуля, поэтому система имеет единственное решение. Покажем, что это решение близко к собственному вектору x_i, соответствующему собственному значению l _i.

Ограничимся случаем, когда матрица n-го порядка A имеет n линейно-независимых собственных векторов x_j, j = 1,…,n. В этом случае собственные векторы образуют базис, по которому можно разложить векторы x и b из (20), т.е.

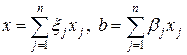. (21)

После подстановки (21) в (20) и при учете того, что 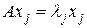, находим

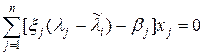. (22)

Поскольку система собственных векторов x_j, j = 1,…,n линейно-независима, постольку 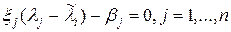, т.е.

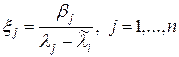. (23)

Согласно формуле (23), один из коэффициентов разложения x _j велик при 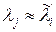. Это обстоятельство является решающим в методе обратных итераций. Уточним его для нескольких случаев.

Случай №1. Пусть собственное значение l _i является простым, тогда среди коэффициентов разложения 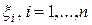, согласно (23), коэффициент 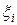является большим, т.е. вектор x с точностью до нормировки близок вектору x_i.

Таким образом, согласно (23), в методе обратной итерации собственный вектор отыскивается тем лучше, чем точнее известно соответствующее собственное значение. Если собственное значение известно слишком грубо или вектор b выбран неудачно так, что x и x_i отличаются значительно, организуют итерационный процесс в следующем виде:

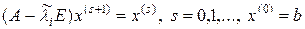Расчеты показывают, что итерационный процесс сходится достаточно быстро (достаточно одной двух итераций), при этом на каждом шаге рекомендуется нормировать .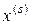

Случай №2. Пусть собственное значение l _i является кратным, кратности p > 1 и ему соответствует p линейно-независимых собственных вектора x₁,…,x_p. В этом случае векторы x₁,…,x_p определяются неоднозначно, т.к. любая их линейная комбинация является собственным вектором. Действительно, имеем следующую цепочку верных равенств

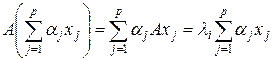т.е. система векторов x₁,…,x_p порождает подпространство, в котором можно выбрать произвольный базис. Векторы, составляющие выбранный базис, могут быть рассмотрены в качестве искомых собственных векторов.

В этом случае, согласно (23), в разложении вектора x будут усилены несколько компонент x₁,x₂,…,x _p, причем в одинаковой степени, т.е. вектор x будет линейной комбинацией векторов x₁,…,x_p. Чтобы найти все линейно-независимые векторы x₁,…,x_p, необходимо применить метод обратных итераций для p линейно-независимых векторов b₁,…,b_p.

Случай №3. Пусть собственное значение l _i является кратным, кратности p > 1 и ему соответствует q (q < p) линейно-независимых собственных вектора x₁,…,x_q. В этом случае также применим метод обратных итераций в форме предыдущего случая. Единственное отличие состоит в том, что среди векторов обратной итерации x⁽^k⁾, соответствующих правым частям b_k, лишь q векторов являются линейно-независимыми, что выясняется при использовании процедуры ортогонализации.

Количество арифметические операций в методе обратных итераций складывается из нахождения собственного вектора » n³ операций, число же собственных векторов » n , т.е. всего » n⁴ операций. Таким образом, при больших n метод неэкономичен, но при n небольших (в пределах нескольких сотен) он вполне приемлем, т.к. прост, универсален и устойчив.

На листинге_№5 приведен код программы для поиска собственных векторов матрицы, у которой все собственные значения простые. Кроме того, собственные значения считаются известными, быть может, и с некоторой погрешностью. В качестве примера матрицы берется трехдиагональная матрица Q (18) из предыдущего пункта.

Листинг_№5

%Программа поиска собственных векторов матрицы

%с помощью метода обратной итерации на примере

%трехдиагональной матрицы

%очищаем рабочее пространство

clear all

%определяем максимальный порядок матрицы A=Q

nmax=200;

%задаем параметр матрицы A=Q

q=0.1;

%организуем цикл расчетов собственных векторов

%для матриц различных порядков (от 1 до nmax)

for n=1:nmax

%формируем трехдиагональную матрицу

%A=Q порядка n

A=zeros(n);

for i=1:n

A(i,i)=1+2*q;

end

for i=2:n

A(i,i-1)=-q;

end

for i=1:(n-1)

A(i,i+1)=-q;

end

%цикл расчета собственных векторов методом

%обратной итерации

for k=1:n

%определяем собственное значение

lambda(k)=1+4*q*sin((pi*k)/(2*(n+1)))^2;

%возмущаем собственное значение

lambda(k)=lambda(k)+1e-5*randn;

%формируем правую часть системы уравнений

%метода обратной итерации

b=randn(n,1);

%организуется итерационный процесс метода

%обратной итерации с тремя итерациями

x0=b;

for j=1:3

%решаем систему обратной итерации

x1=(A-lambda(k)*eye(n))\x0;

x0=x1/norm(x1);

end

%формируется матрица, в которой столбцами

%являются собственные вектора матрицы A=Q

for j=1:n

ev(j,k)=x0(j);

end

%оценивается точность найденных собственных

%векторов для каждого порядка матрицы

error(n)=0;

for k=1:n

error(n)=error(n)+...

norm((A-lambda(k)*eye(n))*ev(:,k));

end

%рисуется зависимость погрешности вычисления

%собственных векторов от порядка матрицы

plot(1:nmax,error);

На рис.5 приведена зависимость итоговой ошибки численной оценки собственных векторов методом обратной итерации от порядка матрицы. Ошибка оценивалась по формуле error = 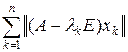. Анализ графика показывает, что ошибка вполне удовлетворительна вплоть до порядка матрицы n = 200.

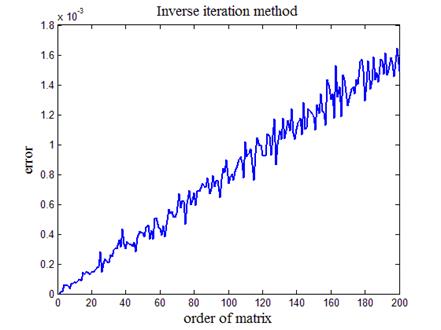
Рис.5. Зависимость численной оценки собственных
векторов от порядка матрицы

Метод отражения

Современные экономичные и устойчивые методы нахождения всех собственных значений основаны на приведении матрицы преобразованиями подобия к той или иной упрощенной форме. Такой упрощенной формой может быть треугольная матрица (верхняя или нижняя), почти треугольная, трехдиагональная или другая форма, для которой проблема собственных значений легко решается.

В данном разделе рассмотрим метод отражений, позволяющий любую матрицу преобразовать к почти треугольной форме за (10/3)n³ арифметических действий, а эрмитову матрицу к трехдиагональной форме за (4/3)n³ арифметических операций. Поскольку поиск собственных значений трехдиагональной матрицы экономичен (см. соответствующий пример выше), постольку метод отражений для эрмитовых матриц является одним из самых быстрых.

Введем операцию отражения в n-мерном пространстве относительно некоторой гиперплоскости G, проходящей через начало координат. Схема операции отражения вектора y относительно гиперплоскости G представлена на рис.6. Гиперплоскость характеризуется вектором нормали w. Произвольный вектор y раскладывается на две составляющие: параллельную вектору w и равную 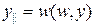и перпендикулярную вектору w и равную y_∟ = y - w(w,y), где скалярное произведение (…,…) определено формулой:

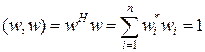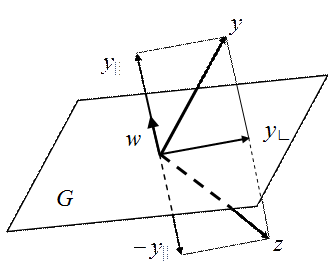
Рис.6. Схема отражения вектора y относительно
гиперплоскости G

При отражении вектора y его перпендикулярная составляющая y_∟ не меняется, а параллельная составляющая меняет знак. В результате отраженный вектор z есть разность z = y_∟ - y_|| или

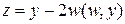. (24)

Преобразование отражения (24) можно записать в канонической форме, вводя матрицу отражения R:

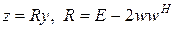(25)

или в координатной форме

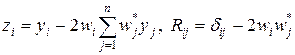. (25¢)

Перечислим без доказательства (доказательства просты и могут быть проделаны самостоятельно) основные свойства матрицы отражения, определенной в (25), (25¢):

· матрица эрмитова, т.е. R = R^H;

· квадрат матрицы отражения равен единичной матрице, т.е. R² = E или, в другой форме, матрица отражения равна своей обратной R = R^-¹;

· из предыдущих двух пунктов следует, что матрица отражения является унитарной, т.к. верно равенство R^H = R^-¹.

Последнее свойство особенно важно в методе отражения, поскольку известно, что при преобразованиях подобия с помощью унитарной матрицы свойство эрмитовости сохраняется. По этой причине, если в рамках метода отражения удастся привести матрицу к почти треугольной форме, то, в силу сохранения свойства эрмитовости, матрица будет трехдиагональной.

Покажем, что для произвольной матрицы можно подобрать последовательность подобных преобразований отражения, которые приведут матрицу к верхней почти треугольной форме. Будем считать, что уже обнулены первые q - 1 столбцов в нижней части матрицы. Разобьем полученную матрицу на клетки так, как это изображено на рис.7.

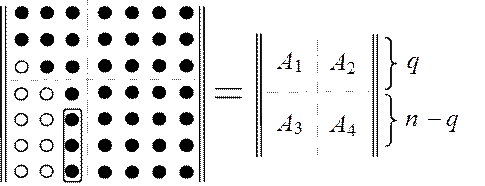
Рис.7. Иллюстрация процедуры приведения матрицы к почти
треугольной форме методом отражений

На рис.7 черные кружки содержат ненулевые элементы матрицы, а белые — нулевые. Клетка A₁ уже приведена к почти треугольному виду, а у прямоугольной матрицы A₃ последний столбец содержит ненулевые элементы. Обведенная группа черных кружков в клетке A₃ обозначает те элементы матрицы, которые должны быть обнулены на q-м шаге.

Определим вектор 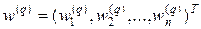, описывающий матрицу отражения, которая после преобразования подобия обнуляет элементы матрицы, обведенные замкнутой линией на рис.7. В дальнейшем индекс q, у вектора w будет для простоты опущен. Вектор w определим в виде:

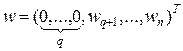. (26)

Согласно (26), матрица отражения (25), (25¢) может быть представлена в следующем блочно-диагональном виде:

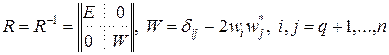. (27)

Из курса линейной алгебры известно, что, если матрицы представлены в одном и том же блочно-диагональном виде, то их перемножение можно осуществлять по обычным правилам матричного умножения, считая матричные клетки как обычные матричные элементы. Осуществим преобразование подобия с матрицей отражения (27), тогда

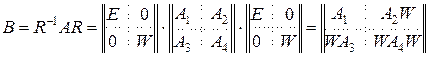. (28)

Клетка A₁ в (28) уже приведена к почти треугольной форме. Осталось рассмотреть клетку WA₃ и добиться ее обнуления. Непосредственной проверкой можно убедиться в том, что в матрице WA₃ все столбцы нулевые, кроме последнего столбца, который можно представить в виде:

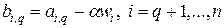, (29)

где

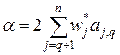. (30)

Исходя из представления (29) добьемся того, чтобы все элементы столбца, кроме самого верхнего обратились в нуль. Это сделать легко, положив

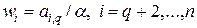. (31)

Из (29) найдем также w_q ₊₁, т.е.

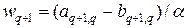. (32)

Подставляя (31), (32) в условие нормировки (w,w) = 1, находим

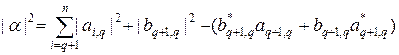. (33)

С другой стороны, подставляя (31), (32) в (30), находим

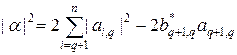. (34)

Согласно (34), можно заметить, что 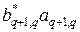вещественное выражение, а после вычитания уравнения (34) из (33), найдем

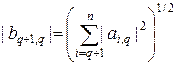. (35)

После подстановки (35) в (34), имеем

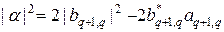. (36)

Второй член в правой части (36) должен быть вещественным, т.е.

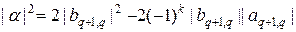(37)

где

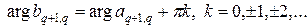(38)

Поскольку в формулах (31), (32) при определении вектора нормали к гиперплоскости отражения нам приходится делить на a, постольку выгодно выбрать нечетное значение k в формуле (37), чтобы не столкнуться с возможностью деления на нуль или близкое к нулю значение. В итоге можно получить

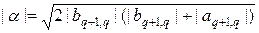. (39)

Заметим, что матрица отражения (27) не меняется при замене 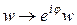, при этом a, согласно (30), заменяется на 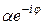. С учетом неопределенности аргумента числа a, формулу (39) в оценке a можно считать завершающей.

Если преобразуется чисто вещественная матрица A, то переход от (36) к (39) сводится к преобразованию:

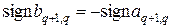. (40)

Формулы (31), (32), (35), (38) — (40) полностью определяют преобразование подобия от матрицы A к матрице B с помощью матрицы отражения R.

Приведенная процедура разобрана для случая обнуления нижней части q-го столбца. Всего необходимо обработать n - 2 первых столбцов матрицы, т.е. q = 1,2,…,n - 2, чтобы произвольная матрица A преобразовалась в верхнюю почти треугольную матрицу S, а эрмитова — в трехдиагональную. Если 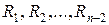— матрицы отражения, последовательно преобразующие матрицу A к верхнему почти треугольному (трехдиагональному) виду, то

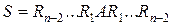Как уже упоминалось ранее, после приведения матрицы к верхней почти треугольной (трехдиагональной) форме легко можно найти собственные значения и собственные вектора y_i. Собственные значения преобразованной матрицы S такие же, как и у матрицы A, а собственные вектора вычисляются по формуле .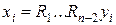

Подсчет числа арифметических операций при экономном использовании метода отражения дает следующие оценки для эрмитовой матрицы: на подсчет всех собственных значений требуется 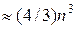операций, для нахождения всех собственных векторов — еще 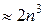. Для решения полной проблемы собственных значений эрмитовых матриц метод отражений один из самых быстрых и устойчивых методов.

В пакете MATLAB приведение матрицы к верхней почти треугольной форме с помощью преобразования подобия унитарной матрицей осуществляется функцией hess. Это же преобразование в пакете MATLAB называется разложением Хессенберга. Типичное обращение к разложению Хессенберга выглядит следующим образом: [R,S] = hess(A), A = RSR^H.

На листинге_№6 приведен код программы преобразования произвольной матрицы к верхней почти треугольной форме с помощью метода отражения по формулам (27), (28), (31), (32), (35), (38) — (40). Вычисляется время работы центрального процессора по преобразованию матрицы в зависимости от ее порядка и эта зависимость сравнивается с аналогичной, но при использовании встроенной в MATLAB функции hess, которая осуществляет такое же преобразование матрицы и тем же методом отражения.

Листинг_№6

%Программа приведения матрицы к верхней почти

%треугольной форме методом отражения

%очищаем рабочее пространство

clear all

%определяем максимальный порядок матрицы

nmax=403;

%организуем цикл преобразований матриц разного

%порядка

for n=3:20:nmax

%запоминаем начало работы процессора при

%преобразовании матрицы

t0=cputime;

%создаем случайную матрицу

A=randn(n);

%определяем цикл q-2 подобных

%преобразований отражения

for q=1:(n-2)

u=0;

for i=(q+1):n

u=u+abs(A(i,q))^2;

end

%согласно теории вычисляем b(q+1,q)

bq1q=sqrt(u);

alpha=sqrt(2*bq1q*(bq1q+abs(A(q+1,q))));

%формируем вектор нормали w к плоскости

%отражения

w=zeros(n,1);

w(q+1)=(A(q+1,q)+bq1q*sign(A(q+1,q)))/alpha;

for i=(q+2):n

w(i)=A(i,q)/alpha;

end

%вычисляем матрицу отражения R при текущем

%значении вектора w

for i=1:n

for j=1:n

if i==j

R(i,j)=1-2*w(i)*w(j);

else

R(i,j)=-2*w(i)*w(j);

end

%осуществляем подобное преобразование матрицы A

%с помощью матрицы отражения R

B=R*A*R;

A=B;

end

%определяем время потраченное центральным процессором

%на преобразование матрицы A к верхнему почти

%треугольному виду методом отражения

t(n)=cputime-t0;

%аналогичную процедуру оценки времени центрального

%процессора проводим при использовании разложения

%Хессенберга с помощью функции hess

t0=cputime;

B=hess(randn(n));

thess(n)=cputime-t0;

end

%рисуем в одном окне график зависимости времени работы

%центрального процессора по преобразованию матрицы от

%порядка матрицы для нашей программы (маркер *) и для

%встроенной в MATLAB программы hess (марке "пентаграмма")

plot(3:20:nmax,t([3:20:nmax]),'-*',...

3:20:nmax,thess([3:20:nmax]),'-p');

На рис.8 приведена итоговая пара кривых производительности центрального процессора компьютера. Видно, что наша программа заметно уступает по производительности встроенной в MATLAB функции. Этому есть объяснение. Преобразование подобия по формуле (28) осуществлено в программе листинга_6 не оптимально. Предлагается самостоятельно так модифицировать код программы, чтобы приблизиться к производительности встроенной функции hess.

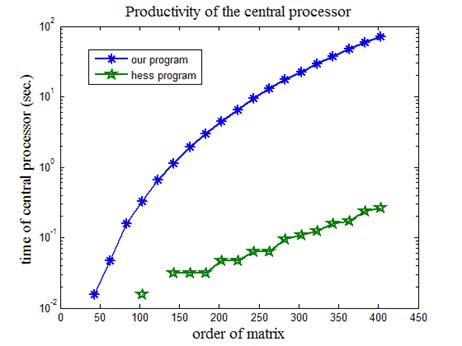
Рис.8. Сравнение производительности центрального
процессора для двух программ

Помимо метода отражения, используется также так называемый метод вращений[1]. И тот и другой методы относятся к прямым методам преобразования матриц к верхнему почти треугольному виду.

Наряду с прямыми методами разработаны и используются итерационные методы. К ним относится, например, метод Якоби, который преобразует эрмитову матрицу в диагональную с помощью преобразований вращения. В целом итерационные метод Якоби уступает по скорости методу отражений, его основное преимущество — надежность и единообразие вычисления всех собственных значений и собственных векторов. К итерационным методам относится также метод обобщенных вращений (развитый Эберлейн и В.В. Воеводиным), ортогональный степенной метод (предложен В.В. Воеводиным), треугольный степенной метод (предложен Бауэром), QR — алгоритм (предложен В.Н. Кублановской и Френсисом) основан на преобразовании матрицы к треугольной форме и ряд других алгоритмов.

Дата добавления: 2022-01-22; просмотров: 84; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!