Интерполяционный многочлен Лагранжа
Лекция №2
Аппроксимация функций
Полиномиальный метод интерполяции
Пусть определена некоторая функция y = f(x). Это означает, что задан закон f, по которому каждому значению x из некоторого множества соответствует некоторое y из соответствующего множества. В такой общей постановке функция f может быть как угодно сложно устроенной, при этом всегда имеется некоторая информация об этой функции. Например, могут быть известны: значения функции на некотором наборе точек, ряд ее производных в том или ином наборе точек, интегралы на тех или иных подмножествах. В задачах математической физики искомая функция может оказаться экстремалью некоторого функционала. Кроме того, возможны любые комбинации перечисленных вариантов. С точки зрения вычислительных методов можно попытаться построить более простую функцию f, которая по определенному критерию является приближением к исходной функции. В дальнейшем ограничимся рассмотрением случаем функций одной переменной.
Пусть на оси x задана сетка w n = {xi, i = 1,2,…,n}, определяющая n точек x1 < x2 < … < xn. На этой сетке определена неизвестная функция f, т.е.
y1 = f(x1), y2 = f(x2), … ,yn = f(xn).
Требуется найти функцию y = f(x), которая принимает в точках x1, x2, …, xn те же значения, что и функция f: y1, y2, …, yn, т.е. f(xi) = yi, i = 1,2,…,n. В этом случае точки x1, x2, …, xn называются узлами интерполяции, а искомая функция y = f(x) — интерполирующей.
Геометрически процедура интерполяции означает, что на плоскости необходимо построить кривую, которая проходит через множество точек (xi,yi), i = 1,2,…,n. Задача интерполяции является неоднозначной, т.к. можно провести бесконечно много кривых через заданный набор точек.
|
|
|
Решение задачи интерполяции позволяет в принципе вычислить значение функции f в произвольной точке x * оси x. При этом если x * Î [x1,xn], то задача вычисления функции в точке x * называется интерполяцией, если x *Ï [x1,xn] — экстраполяцией.
Если в качестве интерполирующей функции выбрать полином степени n -1, то задача интерполяции имеет единственное решение. Действительно полином степени n -1 определяется n значениями свободных параметров a1,a2,…,an согласно формуле:
f(x) = a1 + a2x + … +anxn -1. (1)
Удовлетворим условиям интерполяции: f(xi) = yi, i = 1,2,…,n, тогда получается следующая линейная относительно неизвестных коэффициентов a1,a2,…,an система уравнений:
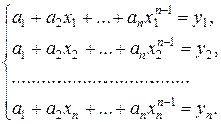(2)
Система уравнений (2) имеет единственное решение, т.к. определитель ее матрицы является определителем Вандермонда, который, как известно из курса линейной алгебры, отличен от нуля, когда все точки x1, x2, …, xn различны.
|
|
|
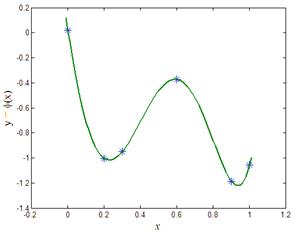
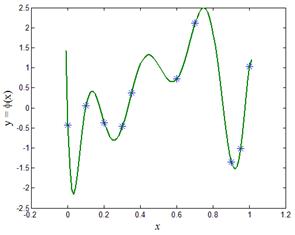
Пример №1. Построим интерполяционные полиномы согласно решению системы уравнений (2) в двух случаях для числа узлов интерполяции 6 и 10 соответственно.
На листинге_№1 приведен код соответствующей программы, а на рис.1 графики полиномов.
Листинг_№1
%Полиномиальная интерполяция
%определим вектор узлов интерполяции
x=[0 0.1 0.2 0.3 0.35 0.6 0.7 0.9 0.95 1];
%определим значения интерполируемой функции
%считая эти значения случайными величинами,
%распределенными по нормальному закону
y=[];
for i=1:length(x)
y=[y;randn];
end
%решаем систему уравнений (2) и находим
%вектор-столбец коэффициентов полинома
a=vander(x)\y;
%строим интерполирующую функцию
xv=-0.01:0.01:1.01;
phi=polyval(a,xv);
%строим график интерполирующей функции,
%а маркерами метим значения функции в
%узлах интерполяции
plot(x,y,'*',xv,phi);
Визуальное сравнение двух графиков на рис.1 показывает, что качество интерполирующей функции быстро ухудшается с ростом числа узлов интерполяции и соответственно степени аппроксимирующего полинома. Разберемся с этим вопросом более подробно. Для этого определим норму для интерполирующей функции.
Пусть определен интервал интерполяции w = [a,b]. Введем норму для функции f(x):
|
|
|
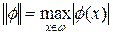. (3)
Будем различать два случая: интерполяция в узком смысле слова, когда a = x1 < x2< … < xn = b и интерполяция вместе с экстраполяцией, когда интервал w включает узлы интерполяции, т.е. a < x1 < x2< … < xn < b.
| 
|
| Рис.1,а. Интерполяция по 6 узлам | Рис.1,б. Интерполяция по 10 узлам |
На листинге_№2 приведен код программы расчета нормы интерполирующей функции. На рис.2 приведены результаты расчета нормы интерполирующей функции.
Листинг_№2
%Скрипт для оценки нормы интерполирующей
%функции согласно формуле (3)
clear all;
%определяем интервал оценки нормы
a=0.0; b=1.0;
%максимальное количество узлов интерполяции
nmax=16;
%цикл перебора интерполяционных полиномов
%с числом узлов интерполяции от 3 до nmax
for i=3:nmax
h=1.0/(i-1);
x=0:h:1;
nor(i-2)=interpol(x,a,b);
end
%визуализация графика зависимости нормы
%интерполирующей функции от числа узлов
%интерполяции
n=3:nmax;
plot(n,nor);
%создаем отдельный файл interpol.m под
%функцию interpol
%Полиномиальная интерполяция
function norm=interpol(x,a,b)
%определим значения интерполируемой функции
%считая эти значения случайными величинами,
%распределенными по нормальному закону
|
|
|
y=[];
for i=1:length(x)
y=[y;randn];
end
%решаем систему уравнений (2) и находим
%вектор-столбец коэффициентов полинома
coef=vander(x)\y;
%строим интерполирующую функцию
xv=a:0.01:b;
phi=polyval(coef,xv);
%возвращаем значение нормы интерполирующей
%функции
norm=max(abs(phi));
| 
|
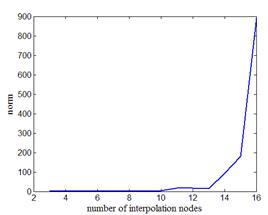
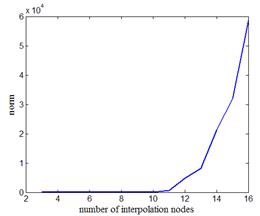
| Рис.2,а. Зависимость нормы интерполирующей функции, когда a = x1 и b = xn | Рис.2,б. Зависимость нормы интерполирующей функции, когда a < x1 и b > xn |
Анализ рис.2 позволяет сделать следующие выводы. Поскольку норма интерполирующей функции (2) сильно растет после превышения числа узлов интерполяции значения 10¸12, постольку практическое использование метода полиномиальной интерполяции в постановке (2) сильно ограничено. На рис.2,а норма интерполирующей функции вычислялась только для отрезка интерполирования, когда a = x1 и b = xn. На рис.2,б норма интерполирующей функции вычислялась с учетом экстраполяции, когда a < x1 и b > xn. Включение в отрезок нормы областей экстраполяции, как нетрудно увидеть из рис.2,б, увеличило норму еще на два порядка.
Интерполяционный многочлен Лагранжа
Представим интерполирующий полином в следующем виде:
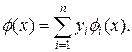(4)
где y1, y2,…, yn — значения интерполируемой функции в узлах интерполяции x1, x2,…, xn. Наложим на полиномы f i(x), i = 1,…,n следующие условия:
f i(xi) = 1, i = 1,…,n; f i(xj) = 0, i ¹ j, i,j = 1,…,n. (5)
Условие (5) обеспечивает точное совпадение интерполируемой функции с интерполирующей, т.е. f(xi) = yi, i = 1,…,n.
Учитывая (5), нетрудно построить полиномы f i(x), i = 1,…,n:
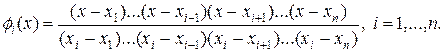(6)
Подставляя (6) в (4), получаем интерполяционный полином Лагранжа n-1 степени:
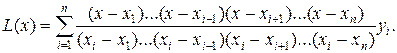(7)
На листинге_№3 приведен код программы, которая строит интерполяционный полином Лагранжа по заданному набору значений интерполируемой функции на соответствующем наборе узлов интерполяции.
Листинг_№3
%Интерполяция с помощью полинома Лагранжа
%определим отрезок интерполяции
a=0.0; b=1.0;
%определим вектор узлов интерполяции
x=[0 0.1 0.2 0.3 0.35 0.6 0.7 0.9 0.95 1];
%определим значения интерполируемой функции,
%считая эти значения случайными величинами,
%распределенными по нормальному закону
y=[];
for i=1:length(x)
y=[y randn];
end
%вводим сетку на отрезке интерполяции
xv=a:0.01:b;
%организуем цикл расчета значений
%интерполирующей функции в узлах сетки
for i=1:length(xv)
yv(i)=lagrange(x,y,xv(i),a,b);
end
%рисуем полином Лагранжа
plot(x,y,'*',xv,yv);
%создаем отдельный файл lagrange.m под
%функцию lagrange
%функция для расчета значений полинома
%лагранжа в точке xz
function yz=lagrange(x,y,xz,a,b)
L=0;
for i=1:length(x)
%вычисляем числитель и знаменатель
%дроби в (7)
numerator=1.0; denumerator=1.0;
for j=1:length(x)
if i~=j
numerator=numerator*(xz-x(j));
denumerator=denumerator*(x(i)-x(j));
end
end
L=L+(numerator/denumerator)*y(i);
end
yz=L;
На рис.3 приведен вариант построения интерполяционного полинома Лагранжа по значениям случайной функции в десяти узлах интерполяции.
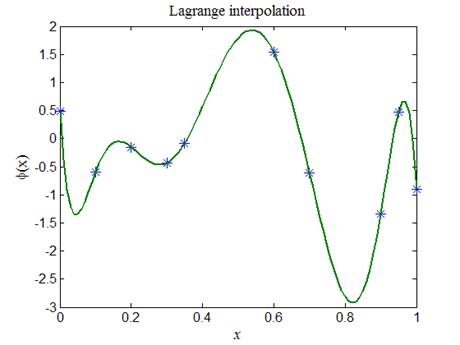
Рис.3. Пример лагранжевой интерполяции по десяти узлам
Оценим погрешность интерполяции многочленом Лагранжа. При оценке значений интерполируемой функции y = f(x) вне узлов интерполяции возникает погрешность R(x), т.е. f(x) = L(x) + R(x). Поскольку в узлах интерполяции R(xi) = 0, i = 1,…,n, постольку ошибку интерполяции можно представить в виде R(x) = w(x)r(x), где w(x) = (x - x1)(x - x2)…(x - xn). Для оценки выражения r(x) введем функцию q(x) = f(x) - L(x) - w(x)r(x *), где x * — произвольное значение на оси x. По построению функция q(x) обращается в ноль в n +1 точках, т.е. q(xi) = 0, i = 1,…,n и q(x *) = 0.
Будем считать, что интерполируемая функция f обладает n непрерывными производными. Поскольку между двумя нулями гладкой функции лежит ноль ее производной, постольку q¢(x) обращается в ноль, по крайней мере, в n точках. Применяя данную процедуру n-1 раз, получаем, что между двумя нулями функции q(n -1)(x) находится, по теореме Ролля, по крайней мере один корень x функции q(n)(x), т.е. q(n)(x ) = f(n)(x ) - n! r(x *) = 0. Таким образом, r(x *) = f(n)(x )/ n!. Поскольку x * произвольная точка, постольку можно считать, что
,
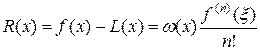где xÎ(a,b). Обычно точка x неизвестна, поэтому на практике используют мажорантную оценку погрешности интерполяции вида:
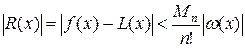, (8)
где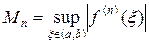 
.
Оценка (8) выступает в качестве примера априорной оценки точности, т.е. если нам известен вид интерполируемой функции, то, до начала проведения вычислений, можно определить точность процедуры интерполирования.
Разобранные выше способы интерполяции обладают явным недостатком: при повышении степени полинома, начиная со степени 10¸12, размах колебаний интерполяционного полинома становится неприемлемым. Дальнейшее повышение качества аппроксимации табличных функций можно достигнуть с помощь сплайнов.
Сплайны
Английское слово spline можно перевести, как “гибкая линейка”. Сплайны, в отличие полиномиальной интерполяции предыдущих пунктов, представляют собой полиномы невысокой степени, например, первой или третьей. Строятся они не глобально для всего отрезка интерполяции, а применительно к более мелкому отрезку между парой узлов интерполяции. При этом принято обеспечивать совпадение значений соседних сплайнов в узлах интерполяции и, быть может, непрерывность первых или вторых производных сплайнов интерполирующей функции. Техника сплайнов может быть еще охарактеризована как процедура построения кусочно-полиномиальной интерполяции.
Более подробно рассмотрим наиболее употребляемый кубический сплайн. Пусть искомая функция f задана в n узлах интерполяции x1,…,xn своими значениями y1,…,yn. На отрезке [xi,xi+1] определим кубический сплайн вида si(x) = ai + bix + cix2 + dix3, Всего, таким образом, можно определить n-1 сплайнов si(x), где i = 1,…,n-1. Для определения 4(n-1) неизвестных ai, bi, ci, di, i = 1,…,n-1, составим n условий совпадения значений сплайна со значениями интерполируемой функции:
si(xi) = yi, i = 1,…,n-1; sn -1(xn) = yn; (9)
n-2 условий непрерывности сплайна:
si(xi+1) = si+1(xi+1), i = 1,…,n-2; (10)
n-2 условий непрерывности производной сплайна:
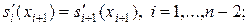(11)
n-2 условий непрерывности второй производной сплайна:
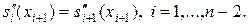(12)
Всего, таким образом, на 4n-4 неизвестных сплайна накладывается 4n-6 уравнений. Недостающие два уравнения обычно определяют, исходя из тех или иных граничных условий. Предположим, например, что функция f на своих границах удовлетворяет условиям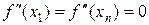 
, тогда имеем следующую недостающую пару уравнений:
c1 + 3d1x1 = 0, cn -1 + 3dn -1xn = 0. (13)
Уравнения (9) — (13) однозначно определяют кубический сплайн s = s(x). Для изучения процесса сходимости сплайна к интерполируемой функции сформулируем без доказательства теорему. Для формулировки теоремы введем ряд предположений.
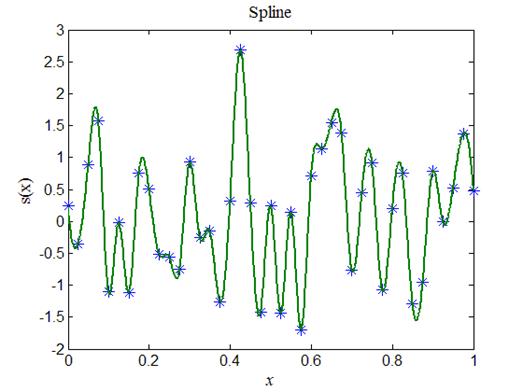
Рис.4. Пример построения кубического сплайна по 41 узлу интерполяции
Пусть интерполируемая функция задана на равномерной сетке xi, i = 1,…,n, xi = (i-1)h, где h = 1/(n-1) — шаг сетки. Пусть функция f имеет четвертую производную, т.е. относится к классу функций C(4) и, кроме того,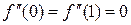 
. Пусть кубический сплайн s(x) удовлетворяет тем же условиями, т.е. 
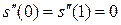, тогда после введения обозначений
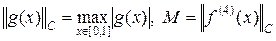
можно сформулировать теорему об оценке ошибки интерполяции для функции f(x) и ее производных f¢(x), f¢¢(x).
Теорема[1]. Для fÎC(4) справедливы оценки
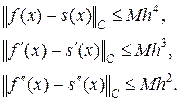(14)
Из оценок (14) следует, что при h ® 0 (n ® ¥) не только сплайн сходится к интерполируемой функции, но и его первая и вторая производный сходятся к соответствующим производным интерполируемой функции.
Займемся теперь программированием сплайнов. На листинге_№4 приведен код программы для построения кубического сплайна. На рис.4 приведен пример расчета сплайна.
Листинг_№4
%Интерполяция с помощью сплайна
%определим вектор узлов интерполяции
x=0:0.025:1;
%определим значения интерполируемой функции,
%считая эти значения случайными величинами,
%распределенными по нормальному закону
y=[];
for i=1:length(x)
y=[y randn];
end
%вводим сетку на отрезке интерполяции
xv=0:0.001:1.0;
%обращаемся к стандартной процедуре MATLAB
yv=interp1(x,y,xv,'spline');
%рисуем сплайн
plot(x,y,'*',xv,yv);
| 
|
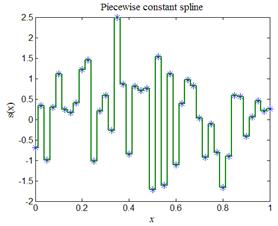
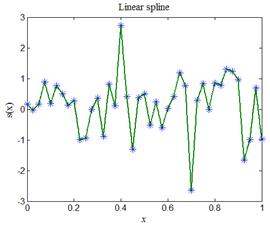
| Рис.5,а. Пример кусочно-постоянного сплайна | Рис.5,б. Пример линейного сплайна |
Стандартная функция interp1 в MATLAB дает возможность также построить кусочно-постоянные сплайны полиномами нулевой степени (способ 'nearest') и линейные сплайны полиномами первой степени (способ 'linear'). На рис.5,а приведен пример кусочно-постоянного сплайна, а на рис.5,б пример линейного сплайна.
Функция interp1 из листинга_№4 допускает еще два способа построения сплайнов: 'pchip' и 'cubic'. В определенном смысле эти способы дают более высокого качества сплайны, чем предыдущие процедуры. Предлагается студентам разобраться с этими режимами построения сплайнов самостоятельно.
Дата добавления: 2022-01-22; просмотров: 70; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!