Примеры математических моделей

Физический факультет

Кафедра компьютерных методов физики

Курс лекций

ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ.
Теория и практика в среде MATLAB

К.Э. Плохотников

Москва, 2007

Лекция №1

Численные методы

Методологическое введение

Дисциплина под названием численные методы часто характеризуется также термином вычислительная математика. Из этих двух названий следует, что в курсе лекций будет представлен набор вычислительных или численных методов, процедур, наиболее употребляемых в современных задачах физики, и, прежде всего, математической физики и вообще во всех тех областях знания, которые принято называть естественнонаучными.

В настоящее время применение численных методов не ограничивается только естественнонаучными областями знания, но и активно востребовано в сфере традиционно относимой к гуманитарной. Это история, политика, экономика, психология и некоторые другие области знаковой деятельности человека[1]. Более того, на примере экономики можно констатировать значительные злоупотребления в использовании математического метода в ущерб содержанию предметной области [2].

Активное продвижение математических методов, математических технологий во все сферы знаковой деятельности человека стало возможным с появлением компьютера в современном смысле слова, т.е. с появлением компьютерной или, более точно, информационной индустрии.

Традиционное использование компьютера в науке, как универсального вычислительного устройства, получило в последнее время новое содержание в рамках таких понятий, как виртуальная реальность и интерактивный интерфейс. Современные вычислительные мощности и средства программирования позволяют в ряде случаев не просто решить ту или иную задачу, но и построить нечто большее — виртуальную реальность или, просто, виртуал, в котором исследователь может осознать решение задачи во всем возможном многообразии. Привлечение средств интерактивного интерфейса позволяет активно манипулировать доступным многообразием для получения оптимального в том или ином смысле решения исходной задачи. В этом контексте курс лекций построен таким образом, чтобы студенты могли непосредственно использовать такой широко известный пакет программирования, как MATLAB для активного овладения вычислительными методами.

С точки зрения внешнего наблюдателя, физика, а также все прочие естественнонаучные отрасли знания представляют собой свод, перечень или набор теорий, моделей, которые могут объединяться в еще более крупные единицы — парадигмы. Теории или модели могут быть насыщены в той или иной мере математикой, тогда они становятся математическими теориями или математическими моделями. Более употребляемым является термин математическая модель, т.к. модели в отличие от теорий представляются более мелкими единицами знания и более разнообразными, они интенсивно генерируются, а также могут активно устаревать, выходя из употребления. Более подробно понятие математическая модель разобрано во введение к монографии К.Э. Плохотникова¹. Грубо говоря, “расстояние” между математическими моделями той или иной предметной области и компьютером в широком смысле слова заполняют вычислительные методы. Вычислительные методы свой наивысший статус — статус вычислительного эксперимента достигают в контексте некоторой математической модели, описывающей тот или иной объект исследования.

Постановка и проведение вычислительного эксперимента нам необходимы не сами по себе, а для контроля и управления объектом исследования. Говоря в более широком смысле слова и уже применительно к моделям любой предметной области, нас, в конечном счете, интересует власть над тем или иным фрагментом природой или социальной реальностями.

Приведенный перечень понятий проиллюстрируем на примере современных методов прогноза погоды. Предметная область или объект исследования может быть назван физикой атмосферы. В частности, физика атмосферы включает ряд математических моделей, описывающих динамику и термодинамику атмосферы в целом. Как известно, для целей прогноза погоды используются уравнения в частных производных Навье-Стокса. Эти уравнения описывают динамику и термодинамику сплошной среды, они традиционно привлекаются для описания движения жидкостей и газов. Чтобы эти уравнения использовать для прогноза погоды, их необходимо дискретизировать, т.е. перейти от континуального описания сплошной среды к дискретному в том или ином смысле описанию. Сам по себе этот переход является одной из основных процедур, обсуждаемых в вычислительных методах. После осуществления процедуры дискретизации становится возможным привлечение компьютеров для расчетов основных метеорологических параметров: скорости, температуры, давления и прочих характеристик. Когда нам, массовым потребителям прогноза погоды, демонстрируют на экране телевизора соответствующие карты, и мы переживаем чувство власти над стихией — это и есть выражение триумфа вычислительных методов в форме вычислительного эксперимента.

Объект исследования допускает множество математических моделей для своего описания. Естественно может возникнуть вопрос: почему моделей множество? Потому, что сам объект исследования не удается раз и навсегда определить, текущая модель и есть одно из возможных определений объекта исследования. Современное положение дел в области моделирования такого, что объект исследования допускает, в общем случае, бесконечно много моделей для своего описания. Основная трудность, стоящая перед исследователем, состоит в проблеме выбора из потенциально бесконечного набора конкурирующих моделей. Более подробно о природе выбора моделей изложено в монографии¹.

На рис.1 приведена схема позиционирования вычислительных методов в рамках так называемого “колеса” научно-технической деятельности. Под колесом или циклом понимается реализация цепочки: объект ® модель ® вычислительные методы ® вычислительный эксперимент ® контроль ® объект¢, где штрих обозначает возврат к исходному объекту исследования, но на другом научно-техническом, познавательном уровне.

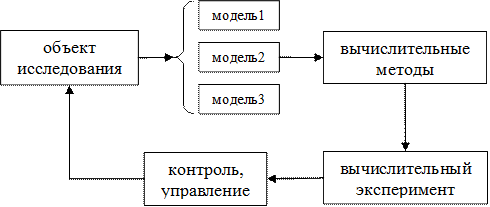
Рис.1. Блок-схема позиционирования вычислительных методов
в рамках “колеса” научно-технической деятельности

Литература по численным методам и среде MATLAB

В основу курса положены следующие учебные материалы по вычислительным методам:

1. Калиткин Н.Н. Численные методы. — М.: Гл. ред. физ.-мат лит., 1978. 512с.

2. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). — М.: Гл. ред. физ.-мат лит., 1973. 631с.

3. Самарский А.А., Гулин А.В. Численные методы: Учеб. Пособие для вузов. — М.: Наука, Гл. ред. физ.-мат лит., 1989. 432с.

4. Демидович Б.П., Марон И.А. Основы вычислительной математики. — М.: Наука, Гл. ред. физ.-мат лит., 1970. 664с.

5. Хемминг Р.В. Численные методы для научных работников и инженеров. — М.: Наука, Гл. ред. физ.-мат лит., 1968. 400с.

а также учебные пособия последних лет:

6. Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам: Учеб. пособие. — М.: Университетская книга, Логос, 2006. 184с.

7. Пирумов У.Г. Численные методы : Учеб. пособие. — М.: Дрофа, 2004. 224с.

8. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах: Учеб. пособие. — М.: Высшая школа, 2006, 480с.

Среда MATLAB для научных и технических математических вычислений изложена во множестве учебных пособий, среди них выделим:

Мартынов Н.Н. Введение в MATLAB6. — М.: КУДИЦ-ОБРАЗ, 2002. 352с.
Дьяконов В.П. MATLAB 6/6.1/6.5+Simulink4/5. Основы применения. Полное руководство пользователя. — М.: СОЛОН-Пресс, 2002. 768с.
Плохотников К.Э., Волков Б.И., Задорожный С.С., Антонюк В.А., Терентьев Е.Н., Белинский А.В. Методы разработки курсовых работ. Моделирование, вычисления, программирование на С/С++ и MATLAB, виртуализация, образцы лучших студенческих курсовых работ: Учеб. пособие/ Под ред. К.Э.Плохотникова. — М.: СОЛОН-ПРЕСС, 2006. 320с.

кроме того отметим имеющиеся учебные материалы по изложению вычислительных методов в среде MATLAB:

Кетков Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB7: программирование, численные методы. — СПб.: БХВ-Петербург, 2005. 752с.
Потемкин В.Г. Вычисления в среде MATLAB. — М.: ДИАЛОГ-МИФИ, 2004. 720с.
Мэтьюз Дж.Г., Финк К.Д. Численные методы. Использование MATLAB. — М.: Издательский дом “Вильямс”, 2001. 720с.
Боглаев Ю.П. Вычислительная математика и программирование. — М.: Высшая школа, 1990. 544с.

Примеры математических моделей

Модель №1: модель маятника. Смоделируем движение маятника в некоторой среде, характеризуемой трением.

На рис.2,а приведен образ маятника, а на рис.2,б его математическая модель в виде дифференциального уравнения. Подробности объекта исследования и его математической модели: груз некоторой массы прикреплен к абсолютно упругому и невесомому стержню длины l, стержень крепится к шарнирной опоре в точке О, f — угол отклонения маятника от вертикального положения, g — ускорение свободного падения, t — время, m — коэффициент трения при движении маятника в некоторой среде. Перечисленные выше словесные оговорки при описании объекта исследования, имеют ввиду отсечение огромного количества иных возможных моделей маятника с учетом других особенностей его определения и моделирования.


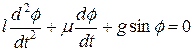
Рис.2,а. Объект исследования — механический маятник	Рис.2,б. Математическая модель механического маятника

На рис.2,б приведена математическая модель движения маятника в виде нелинейного дифференциального уравнения второго порядка. Необходимо решить это уравнение, т.е. найти решения этого уравнения в том или ином смысле. Как правило, уравнения математических моделей не допускают простых аналитических решений, поэтому приходится привлекать численные методы для их решения. Уравнение на рис.2,б именно такое, для него в общем случаю отсутствует решение, выражаемое через обычные функции алгебры и анализа.

Для использования решателей дифференциальных уравнений в пакете MATLAB перепишем уравнение на рис.2,б в следующем виде:

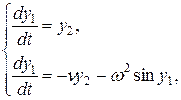(1)

где y₁ =f, y₂ =f ¢, n = m / l, w² = g / l.

Наряду с моделью движения маятника согласно уравнениям (1), рассмотрим также модель линейного маятника, когда считается, что sinf » f. Соответствующие уравнения для описания движения линеаризованного маятника представлены в (2).

(2)

Ниже приведен код программы с комментариями в среде MATLAB, который обеспечивает численное решение систем уравнений (1) и (2) и представление решений в виде графиков на рис.3. Отметим, что в целях упрощения кода программы не используются элементы графического интерфейса (кнопки, редактируемые поля и пр.), которые легко могут быть введены в программу приложения (более подробно с соответствующими процедурами можно ознакомиться в учебном пособии [3] из списка, представленного выше).

Листинг_№1

%MATLAB сценарий или m-сценарий для

%моделирования движения маятника

function pendulum

%определяем значения входных параметров задачи

nu=0.1; omega2=1;

%вводим начальный и конечный моменты времени

tin=0; tfin=30;

%определяем анонимную функцию правых частей

%системы уравнений (1)

f=@(t,y)[y(2);-nu*y(2)-omega2*sin(y(1))];

%обращаемся к одному из решателей

%дифференциальных уравнений в среде MATLAB ode23

%задаем относительную и абсолютную точности

options = odeset('RelTol',1e-3,'AbsTol',[1e-6 1e-6]);

%решаем систему дифференциальных уравнения (1)

[time,z]=ode23(f,[tin tfin],[pi/4 0],options);

%строим график искомого решения

plot(time,z(:,1));

%решение упрощенной линеаризованной модели

%движения маятника (2)

fl=@(t,y)[y(2);-nu*y(2)-omega2*y(1)];

[timel,zl]=ode23(fl,[tin tfin],[pi/4 0],options);

hold on

plot(timel,zl(:,1),'-.');

Действия студентов по запуску программы pendulum следующие: входим в MATLAB, нажимаем File ® New ® M - File, в появившееся окно с помощью буфера обмена загружаем код программы. Если требуется, корректируем код программы и запускаем ее на исполнение с помощью либо кнопки Run, либо — нажатий Debug ® Run, либо просто F 5. MATLAB также запросит имя и место дислокации соответствующего файла.

Рис.3. Решения систем уравнений (1), (2) согласно коду листинга_№1

Изучение листинга_№1 показывает наличие возможности задания уровней относительной и абсолютной погрешностей или соответствующей точности относительной либо (и) абсолютной при решении уравнений (1) и (2). В общем случае различают четыре источника погрешности результата:

· математическая модель;

· исходные данные;

· приближенный метод;

· округления при вычислениях.

Иллюстрация погрешности математической модели приведена на рис.3 при сравнении двух моделей: нелинейной, более реалистичной модели и линейной, упрощенной модели движения маятника.

Приближенным числом a называется число, незначительно отличающееся от точного A и заменяющее последнее в вычислениях. Под ошибкой или погрешностью D a приближенного числа a обычно понимается разность между точным и приближенным значениями, т.е. D a = A - a . Как правило, знак ошибки неизвестен. В этом случае используют абсолютную погрешность приближенного числа D = |D a|. Относительной погрешностью d приближенного числа a называется отношение абсолютной погрешности D к модулю точного числа A, т.е. d = D / |A|. Под предельной абсолютной погрешностью приближенного числа a понимается всякое число D _a , не меньшее абсолютной погрешности этого числа, т.е. D = |A - a| £ D _a. Под предельной относительной погрешностью приближенного числа a понимается всякое число d _a , не меньшее относительной погрешности этого числа, т.е. d £ d _a. Согласно введенным определениям, имеем

a - D _a £ A £ a + D _a или, что то же, A = a ± D _a;

a(1 - d _a) £ A £ a(1 + d _a) или, что то же, A = a(1 ± d _a).

Второе из неравенств получено из предположения о том, что на практике A » a.

Возвращаемся к источнику погрешности результата в исходных данных. Так, согласно работе[3], измерение лэмбовского сдвига d (МГц) в атоме водорода по сравнению с теорией имеет следующую абсолютную точность: d_эксп = 1057,862 ± 0,020; d_теор = 1057,912 ± 0,011. Нетрудно оценить относительную точность измерения и погрешность теоретической оценки: 1,89×10^-⁴ и 1,04×10^-⁵ соответственно. Точность в особых прецизионных измерениях доходит до 10^-¹². Это, конечно, не типичная ситуация в физике и технике. Часто приходится ограничиваться относительной погрешностью измерений от 1% до 10% и более.

Погрешности результата, связанного с особенностями метода, весьма разнообразны. Они выражаются, например, в том, что ряды суммируются с конечным, а не бесконечным числом слагаемых, функции аппроксимируются полиномами с заданной точностью, итерационные процессы прекращаются после конечного числа шагов и пр. Особенности тех или иных вычислительных методов обсуждаются на протяжении всего данного курса.

Погрешности при вычислениях вследствие округлений неизбежны, поскольку на компьютере под числа отводится ограниченное число байт. Например, под число с плавающей запятой типа double в MATLAB отводится 8 байт или 64 бит памяти, что позволяет достигать точность порядка 15 значащих цифр. Отметим, что в MATLAB, в рамках символических вычислений, возможны точные расчеты, однако любая память, отведенная под эти расчеты, может быть быстро исчерпана.

Например, попытка вычислить 1000!, исходя из обычной арифметики, приведет в среде MATLAB к ответу: Inf, что означает машинную бесконечность. Однако если обратиться к символическим вычислениям и набрать команду: Maple 1000! ® Enter, получим точное значение факториала (первые 50 значащих цифр из 2568):

40238726007709377354370243392300398571937486421071…

Поскольку в среде MATLAB мы в основном будем иметь дело с числами с плавающей запятой, т.е. с типом double, постольку важно выяснить каковы минимально (после нуля) и максимально возможные числа. Для этого в MATLAB имеются соответствующие команды: realmin и realmax. Если их выполнить, получим

2.225073858507201e-308 и 1.797693134862316e+308.

Определим понятие корректность — одно из важнейших понятий в вычислительных методах. Некоторая задача называется корректно поставленной, если для любых входных данных из некоторого класса решение существует, единственно и устойчиво по входным данным.

Приведем классический пример некорректно поставленной задачи Коши для эллиптического уравнения в области y ³ 0:

u_xx + u_yy = 0, u(x,0) = 0, u_y(x,0) = j(x). (3)

Входными данными задачи (3) является функция j(x). Очевидно, что, если j(x) = 0, то решение также тривиально, т.е. u(x,y) = 0. Выберем теперь j(x) = j _n(x) = 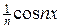, где n = 1,2,… В этом случае решение эллиптического уравнения (3) предстанет в виде:

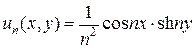. (4)

Очевидно, что j _n(x) равномерно сходится к 0 при n ® ¥, однако, согласно (4), решение u_n(x,y) к нулю при n ® ¥ не сходится, поскольку при y ¹0 решение неограниченно, когда n ® ¥.

Модель №2: модель хищник-жертва Лотки-Вольтерра. Пусть x — плотность популяции жертвы, y — плотность популяции хищника, тогда, согласно модели Лотки-Вольтерра, можно записать следующие уравнения:

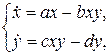(5)

где a, b, c, d=const>0. Коэффициент a описывает интенсивность размножения жертв, b — выедание хищниками жертв, c — увеличение биомассы хищников за счет выедания жертв, d — интенсивность естественной смерти хищников.

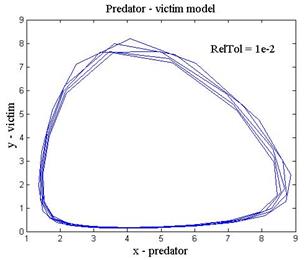
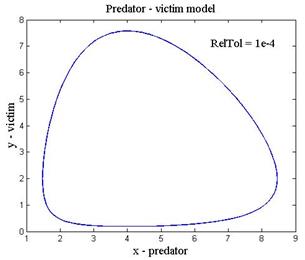
На листинге_№2 приведен соответствующий код программы хищник-жертва, а на рис.4 графики решений в координатах x и y при выборе типичных значений параметров a , b , c , d. На рис.4,а решение получено при относительной точности (параметр решателя RelTol) 10^-², а на рис.4,б — 10^-⁴ соответственно. Решение на рис.4,а мало похоже на искомое решение, решение на рис.4,б вполне годится для представления искомого решения. Сравнение двух графиков на рис.4 отлично иллюстрирует важность контроля за параметром точности (погрешности).

Листинг_№2

%MATLAB сценарий или m-сценарий для

%модели хищник-жертва Лотки-Вольтерра

function predator

%определяем значения входных параметров задачи

a=2; b=1; c=2; d=8;

%вводим начальный и конечный моменты времени

tin=0; tfin=10;

%определяем анонимную функцию правых частей

%системы уравнений (5)

f=@(t,y)[a*y(1)-b*y(1)*y(2);c*y(1)*y(2)-d*y(2)];

%обращаемся к одному из решателей

%дифференциальных уравнений в среде MATLAB ode23

%задаем относительную и абсолютную точности

options = odeset('RelTol',1e-4,'AbsTol',[1e-6 1e-6]);

%решаем систему дифференциальных уравнения (5)

[time,z]=ode23(f,[tin tfin],[1.5 1.5],options);

%строим график искомого решения

plot(z(:,1),z(:,2));


Рис.4,а. Решение системы (5) при относительной точности 1e-2	Рис.4,б. Решение системы (5) при относительной точности 1e-4

Модель №3: молекулярно динамическая модель плавления кристаллического образца.

Согласно методу молекулярной динамики, атомы конечного кристаллического образца описываются классическими уравнениями вида:

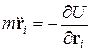, (6)

где m — масса атомов, r_i = r_i(t)— положение i-го атома в пространстве в момент времени t, i=1,2,…, N, N — число атомов в конечном кристаллическом фрагменте. Функция U= U(r₁,…,r_N) — потенциальная энергия всей системы в целом. Выберем потенциал в форме Леннарда-Джонса, т.е.

, (7)

где

. (8)

В (8) коэффициенты подобраны таким образом, чтобы равновесное расстояние между парой атомов равнялось 1, т.е. f ¢(1)=0. В дальнейшем также будем считать массу атомов m единичной величиной, т.е. m=1.

Подставим (7) в (6) с учетом (8), тогда получим:

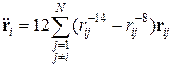, (9)

где r_ij=r_i- r_j, r _ij=|r_ij|. Помимо уравнений молекулярной динамики (9), необходимо определить начальные данные. Представим начальные данные в виде:

. (10)

Для проведения вычислительного эксперимента с уравнениями (9), (10) заменим производные соответствующими конечными разностями по схеме:

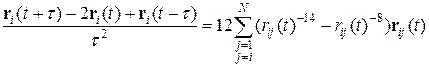, (9¢)

, (10¢)

где t — шаг по времени численного интегрирования системы уравнений (9¢), (10¢).

На листинге_№3 приведен код программы расчета положений 1000 атомов кристаллического образца в зависимости от изменения параметра времени. Всего производится 15 шагов по времени. В рабочем окне можно наблюдать динамику плавления кристаллического образца. В этой модели, поскольку в ней присутствует трехмерное изображение, имеются элементы виртуальной реальности. Итоги моделирования приведены на рис.5.

Листинг_№3

%MATLAB сценарий или m-сценарий для

%молекулярно динамической модели плавления

%кристаллического образца

function MolDynamics

%определим число шагов интегрирования по времени

t=15;

%определим число атомов в кристаллическом образце

n=1000;

%определи начальные положения атомов. Будем считать,

%что все атомы первоначально уложены в узлы

%кристаллической решетки с простой кубической

%симметрией.

for i=1:10

for j=1:10

for k=1:10

x(i+10*(j-1)+100*(k-1))=i-1;

y(i+10*(j-1)+100*(k-1))=j-1;

z(i+10*(j-1)+100*(k-1))=k-1;

end

%определим амплитуду начальной скорости

v0=0.3;

%определим начальные скорости атомов

%кристаллического образца

for i=1:n

vx(i)=v0*(2*rand-1);

vy(i)=v0*(2*rand-1);

vz(i)=v0*(2*rand-1);

end

%определим шаг численного интегрирования

tau=0.05;

%определим положения атомов на втором

%после нулевого временном слое

for i=1:n

x2(i)=x(i)+tau*vx(i);

y2(i)=y(i)+tau*vy(i);

z2(i)=z(i)+tau*vz(i);

end

%создаем рабочее окно и оси трехмерной системы

%координат

hF=figure('NumberTitle','off','Name',...

'Molecular Dynamics','Color',[0.8 0.8 0.8]);

hA=axes('Parent',hF,'Units','pixels',...

'Position',[95 50 350 350]);

axis([-0.5 9.5 -0.5 9.5 -0.5 9.5]);

%рисуем начальные положения атомов

hL=line(x,y,z,'Color','black',...

'LineStyle','none','Marker','.','MarkerSize',18);

pause(0.5);

delete(hL);

%основной цикл по времени

for k=3:(t-1)

for i=1:n

fx=0; fy=0; fz=0;

for j=1:n

if (i~=j)

rij=sqrt((x2(i)-x2(j))*(x2(i)-x2(j))+...

(y2(i)-y2(j))*(y2(i)-y2(j))+...

(z2(i)-z2(j))*(z2(i)-z2(j)));

f14_8=rij^(-14)-rij^(-8);

fx=fx+f14_8*(x2(i)-x2(j));

fy=fy+f14_8*(y2(i)-y2(j));

fz=fz+f14_8*(z2(i)-z2(j));

end

x3(i)=2*x2(i)-x(i)+12*tau*tau*fx;

y3(i)=2*y2(i)-y(i)+12*tau*tau*fy;

z3(i)=2*z2(i)-z(i)+12*tau*tau*fz;

end

for i=1:n

x(i)=x2(i); y(i)=y2(i); z(i)=z2(i);

x2(i)=x3(i); y2(i)=y3(i); z2(i)=z3(i);

end

%рисуем текущее положение атомов

hL=line(x2,y2,z2,'Color','black',...

'LineStyle','none','Marker','.','MarkerSize',18);

pause(0.5);

delete(hL);

end

%рисуем завершающие положения атомов

hL=line(x2,y2,z2,'Color','black',...

'LineStyle','none','Marker','.','MarkerSize',18);

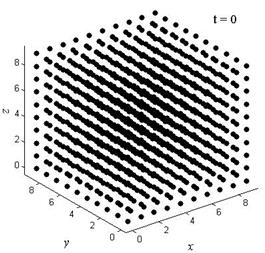
На рис.5,а приведены начальные положения атомов, а на рис.5,б — по прошествии 15 шагов интегрирования.


Рис.5,а. Начальные положения атомов кристаллического образца	Рис.5,б. Положения атомов по прошествии 15 шагов интегрирования

Модель №4: модель колебаний струны u(t,x) (t — время, x — пространственная координата) с закрепленными концами. На рис.6 приведено начальное положение струны. Как известно, колебания струны описываются так называемым волновым уравнением. Формально математически задача формулируется в следующем виде:

u_tt - a²u_xx = 0, u(t,0) = u(t,L) = 0, u(0,x) = u₀(x), u_t(0,x) = 0. (11)

Решение уравнения (11) с соответствующими начальными и граничными условиями можно представить в виде бесконечного ряда:

. (12)

Для представления результата динамики на компьютере ограничимся суммой в (12) с ограниченным числом слагаемых m, т.е. представим решение в виде конечной суммы

. (13)

Рис.6. Начальное положение струны

Учитывая (12), (13), можно оценить погрешность аппроксимации e точного выражения (12) приближенным — (13), т.е.

Задаваясь некоторым значением точности e, можно найти количество слагаемых m, которое надо учитывать при суммировании:

На листинге_№4 приведен код программы, которая рассчитывает положение струны в последовательные моменты времени так, что создается иллюзия динамики. На рис.7 приведен итог моделирования положения струны на некоторый момент времени.

Листинг_№4

%MATLAB сценарий или m-сценарий для

%молекулярно колебаний струны

function String

%определим входные параметры задачи

L=1; h=0.3; x0=0.25; a=1;

%задаемся точностью

eps=1e-3;

%определяем число слагаемых

m=(2*h*L^2)/(pi^2*x0*(L-x0)*eps)-1;

%определяем сетку по времени

t=0:0.1:9.5;

%определяем сетку по пространству

x=0:0.01:L;

%троим рабочее окно

hF=figure('NumberTitle','off','Name',...

'The oscillations of string','Color',[0 1 0]);

hA=axes('Parent',hF,'Units','pixels',...

'Position',[65 50 455 305]);

axis([0 L -h h]);

%производим суммирование

pL=pi/L;

for i=1:length(t)

for j=1:length(x)

uv=0;

for n=1:m

uv=uv+(sin(pL*x0*n)*...

sin(pL*x(j)*n)*cos(pL*a*t(i)*n))/n^2;

end

um(j)=((2*h*L^2)/(pi^2*x0*(L-x0)))*uv;

end

hL=line(x,um,'Color','black');

pause(0.02);

delete(hL);

end

%изображение струны в последний момент времени

line(x,um,'Color','black');

Рис.7. Положение струны в некоторый момент времени

Модель №5: моделирование остановки фронта тепловой волны в нелинейном уравнении теплопроводности.

Рассмотрим нелинейное уравнение теплопроводности, в котором коэффициент теплопроводности степенным образом зависит от температуры T = T(t,x), т.е.

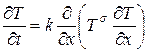, (14)

где k, s = const > 0.

Уравнение (14) решим численно. Для этого введем равномерную сетку по пространству: 0 = x₁ < x₂ <…< x_N = 1, x_i = h(i - 1), i = 1,2,…,N. Таким образом, температура в узлах сетки T_i = T(t,x_i). Запишем теперь неявную разностную схему для решения уравнения (14) вида:

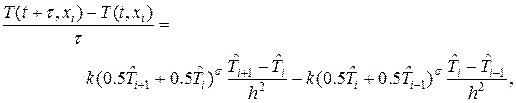(15)

где 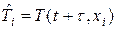искомое значение температуры на следующем временном слое. В (15) t и h = 1/(N - 1) — шаги по времени и по пространству соответственно.

Уравнение (15) порождает нелинейную алгебраическую систему уравнений относительно неизвестной сеточной функции 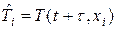. Нелинейную алгебраическую систему уравнений линеаризуем с помощью метода итераций. Пусть индекс s обозначает номер итерации, тогда (15) можно переписать в виде:

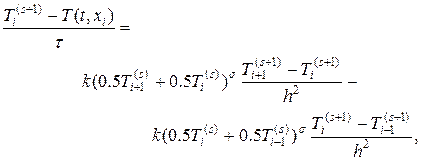(16)

Система уравнений (16) относительно является линейной и может быть решена методом прогонки. Несколько раз решая систему (16), добиваемся того, чтобы верно было неравенство 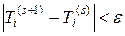для всех i = 1,…,N при выборе некоторого значения уровня точности e. Выполнение неравенства означает сходимость итераций, после чего считается, что = .

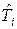На листинге_№5 приведен код программы решения системы уравнений (16) методом прогонки. Результат вычислительного эксперимента представлен на рис.8.

Листинг_№5

%MATLAB сценарий или m-сценарий для решения

%нелинейного уравнения теплопроводности

function heat

%определяем число узлов разностной схемы

N=200;

%вводим точность сходимости итераций и

%максимальное количество итераций на

%каждом временном слое

eps=1e-3; itmax=20;

%определяем шаги по времени и по пространству

tau=0.1; h=1.0/(N-1);

%определяем входные параметры задачи

k=1.0; sigma=4.5; kth=(k*tau)/h^2;

%строим рабочее окно

hF=figure('NumberTitle','off','Name',...

'Thermal conductivity equation','Color',[0 1 0]);

hA=axes('Parent',hF,'Units','pixels',...

'Position',[65 50 455 305]);

axis([0 1.0 0 1.0]);

%строим начальное распределение температуры

%в виде треугольного распределения

for i=1:N

x(i)=h*(i-1);

u(i)=0.0;

if (x(i)>=0.25)&(x(i)<=0.5)

u(i)=4*h*(i-1)-1;

end

if (x(i)>=0.5)&(x(i)<=0.75)

u(i)=3.0-4.0*h*(i-1);

end

%рисуем начальное распределение температуры

line(x,u,'Color','red','LineWidth',3);

pause(0.05);

%для решение нелинейного уравнения теплопроводности

%организуем общий цикл по времени t

for t=1:60

for i=1:N

u1(i)=u(i);

end

for it=1:itmax

%коэффициенты трехточечного шаблона сетки

%a(i)u2(i+1)+b(i)u2(i)+c(i)u2(i-1)=u(i)

for i=2:(N-1)

a(i)=-kth*(0.5*u1(i+1)+0.5*u1(i))^sigma;

b(i)=1.0+kth*(0.5*u1(i+1)+0.5*u1(i))^sigma+...

kth*(0.5*u1(i)+0.5*u1(i-1))^sigma;

c(i)=-kth*(0.5*u1(i)+0.5*u1(i-1))^sigma;

end

%прогонка: u2(i+1)=alpha(i)u2(i)+beta(i)

%обратный ход прогонки с учетом правого нулевого

%граничного условия

alpha(N-1)=0.0; beta(N-1)=0.0;

for i=(N-1):-1:2

alpha(i-1)=-c(i)/(b(i)+a(i)*alpha(i));

beta(i-1)=(u(i)-a(i)*beta(i))/(b(i)+a(i)*alpha(i));

end

%прямой ход прогонки с учетом левого нулевого

%граничного условия

u2(1)=0.0;

for i=1:(N-1)

u2(i+1)=alpha(i)*u2(i)+beta(i);

end

%проверяем как отличаются друг от друга две

%итерации u1(i) и u2(i)

for i=1:N

if abs(u2(i)-u1(i))>eps

for j=1:N

u1(j)=u2(j);

end

break

end

if it==itmax

break

end

for i=1:N

u(i)=u2(i);

end

line(x,u,'Color','black');

pause(0.05);

end

Жирной линией красного цвета на рис.8 изображено начальное распределение температуры. Далее приведены все последующие профили температуры в другие моменты времени. Можно увидеть, что некоторое время после начала динамики фронт тепловой волны не двигается до тех пор, пока профиль волны не достигнет определенной величины выпуклости.

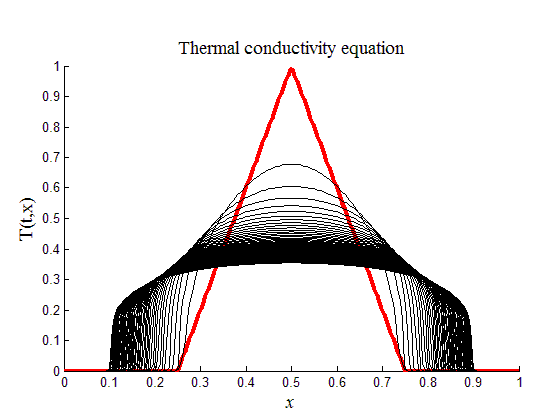
Рис.8. Динамика во времени профиля температуры нелинейного
уравнения теплопроводности (14)

[1] Плохотников К.Э. Математическое моделирование и вычислительный эксперимент. Методология и практика. — М.: Едиториал УРСС, 2003. 280с.

[2] Балацкий Е.В. Профессиональное сообщество экономистов — западная и российская модели// Вестник РАН, 2006, т.76, №1, с.38 — 43.

[3] Соколов Ю.Л., Яковлев В.П. Измерение лэмбовского сдвига в атоме водорода// http://data.ufn.ru//ufn82/ufn82_10/Russian/r8210n.pdf

Дата добавления: 2022-01-22; просмотров: 25; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!