Свойства средней арифметической
Лекция 2.
Вариационные ряды и их характеристики
Основные понятия
Обычно полученные в результате наблюдений данные представляют собой набор чисел. Просматривая этот набор, как правило, трудно выявить какую-либо закономерность. Поэтому данные подвергаются некоторой первичной обработке, целью которой является упрощение дальнейшего анализа.
Итак, предположим, что изучается некоторая случайная величина Х. С этой целью производится ряд независимых опытов, или, наблюдений, в каждом из которых величина Х принимает то или иное значение. Совокупность полученных значений
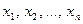 (1)
(1)
(отметим, что некоторые значения могут совпадать). Этот набор чисел называется выборкой (более подробно о выборке см. глава 3).
Опр. Различные значения признака, наблюдающиеся у членов совокупности, называются вариантами, а числа, показывающие, сколько раз встречается каждый вариант – их частотами
Дальнейшие действия зависят от того, насколько много в выборке различных чисел. Если мы имеем дело с дискретной случайной величиной, то различных чисел немного; если с непрерывной случайной величиной, то, скорее всего, все числа окажутся различными. Рассмотрим оба случая.
Дискретный случай. Первый этап обработки – это составление вариационного ряда. Его получают следующим образом: среди чисел (1) отбирают все различные и располагают их в порядке возрастания:
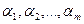 , (2)
, (2)
|
|
|
где 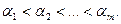
Опр. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им частотами или частостями.
Следующий этап обработки ряда (1) – составление эмпирического закона распределения:
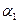
| 
| … | 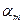
|

| 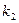
| … | 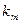
|
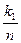
| 
| … | 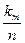
|
Здесь 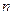 - число всех измерений,
- число всех измерений, 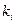 - число измерений, в которых наблюдалось значение
- число измерений, в которых наблюдалось значение  , т.е. частота, а величины
, т.е. частота, а величины 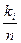 - относительные частоты или частости.
- относительные частоты или частости.
Непрерывный случай. Если число различных значений в выборке велико, вычислять частоту каждого из них не имеет большого смысла. Поэтому поступают следующим образом. Весь промежуток изменения значений выборки, от минимального до максимального, разбивают на интервалы. После этого подсчитывают число значений из выборки, попадающих в каждый интервал (частоты), а затем – относительные частоты. В результате получаем интервальную таблицу частот:
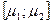
| 
| … | 
|

| 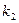
| … | 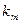
|
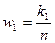
| 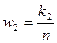
| … | 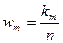
|
Здесь 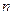 - число всех измерений,
- число всех измерений, 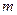 - число интервалов,
- число интервалов, 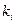 - количество чисел, приходящихся на
- количество чисел, приходящихся на 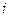 -й интервал,
-й интервал, 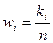 (3) - относительная частота попадания в
(3) - относительная частота попадания в 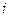 -й интервал.
-й интервал.
Графическое представление данных
Результаты исследования могут быть представлены не только в виде табличном виде, но и в графическом представлении. Графическое представление достаточно часто используется на практике для демонстрации результатов, полученных в ходе проведенного опыта.
|
|
|
При изучении вариационных рядов наряду с понятием частоты используется понятие накопленной частоты (обозначается 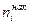 ). Накопленная частота показывает, сколько наблюдалось вариантов со значением признака, меньшим
). Накопленная частота показывает, сколько наблюдалось вариантов со значением признака, меньшим 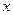 . Отношение накопленной частоты
. Отношение накопленной частоты 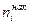 к общему числу наблюдений назовем накопленной частостью
к общему числу наблюдений назовем накопленной частостью 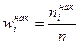 (4) .
(4) .
Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием частот (частостей) всех предшествующих интервалов, включая данный.
Для задания вариационного ряда достаточно указать варианты и соответствующие им частоты (частости) или накопленные частоты (частости).
Для графического изображения вариационных рядов наиболее часто используются: полигон, гистограмма, кумулятивная кривая.
Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломанную, в которой концы отрезков прямой имеют координаты  ,
, 
Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака 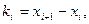
 и высотами, равными частотам (частостям)
и высотами, равными частотам (частостям) 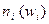 интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
|
|
|
Кумулятивная кривая (кумулята) – кривая накопленных частот (частостей).
Для дискретного вариационного ряда кумулята представляет ломанную, соединяющую точки  или
или 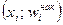 ,
, 
Для интервального вариационного ряда ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте (частости), равной нулю. Другие точки этой ломаной соответствуют концам интервалов.
Весьма важным является понятие эмпирической функции распределения.
Эмпирической функцией распределения  называется относительная частота (частость) того, что признак (случайная величина
называется относительная частота (частость) того, что признак (случайная величина  ) примет значение, меньшее заданного
) примет значение, меньшее заданного 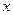 , т.е.
, т.е.
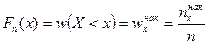 . (5)
. (5)
В теории вероятностей эмпирической функции распределения  отвечает интегральная функция распределения
отвечает интегральная функция распределения 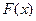 . Свойства
. Свойства  соответствуют свойствам
соответствуют свойствам 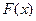 .
.
Свойства:
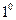 .
. 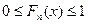 .
.
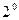 .
.  - неубывающая функция.
- неубывающая функция.
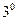 .
.  при
при 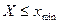 и
и 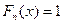 при
при 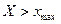 .
.
|
|
|
Кроме гистограммы, полигона и кумуляты также можно использовать диаграмму рассеивания и круговую диаграмму.
Диаграмма рассеивания (точечная диаграмма) используется для нахождения наглядного отображения совместного распределения двух переменных. Этот вид диаграмм позволяет визуально оценить степень связи между изучаемыми признаками.
Эллипс, охватывающий все точки на диаграмме, имеет достаточно вытянутую форму, что свидетельствует о связи между случайными величинами Х, У, а т.к. большая диагональ образует с осью абсцисс острый угол, то связь прямая, что означает, что при увеличении роста животного увеличивается и его масса.
Замечание. Чем более вытянутая форма у эллипса, тем более выражена связь между признакам. Если же угол между большей осью эллипса и осью абсцисс тупой, тогда связь между признаками обратная, т.е. чем больше значение признака Х, тем меньше значение признака У.
Если точки на диаграмме расположены хаотично и вместо эллипса получается окружность, то связи между признаками не существует.
Круговая диаграмма используется для того, чтобы наглядно изобразить соотношение частей (признаков) внутри целого.
Замечание. При построении графических изображений необходимо выполнять следующие требования:
1.Оси координат должны быть перпендикулярны, их пересечение – начало координат – нуль.
2.Разрыв вертикальной оси (оси ординат) не допускается.
3. Разрыв горизонтальной оси (оси абсцисс) изображается как две вертикальные черты (см. рис. 1, 2, 5).
4.Все обозначения ставятся слева и снизу от осей координат.
5.Все подписи под диаграммами должны носить полную информацию.
Средние величины
Средние величины характеризуют значение признака, вокруг которого концентрируются наблюдения или, как говорят, центральную тенденцию распределения. Наиболее распространенной из средних величин является средняя арифметическая.
Опр. Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:
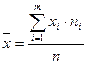 , (6)
, (6)
где  - варианты дискретного ряда или середины интервалов интервального вариационного ряда;
- варианты дискретного ряда или середины интервалов интервального вариационного ряда; 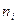 - соответствующие им частоты; т – число неповторяющихся вариантов или число интервалов;
- соответствующие им частоты; т – число неповторяющихся вариантов или число интервалов; 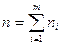 .
.
Или,
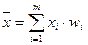 , (7)
, (7)
где 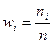 - частости вариантов или интервалов.
- частости вариантов или интервалов.
Свойства средней арифметической
1. Средняя арифметическая постоянной равна самой постоянной.
2. Если все варианты увеличить (уменьшить) в одно и тоже число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
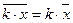 .
.
3. Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число:
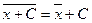 .
.
4. Средняя арифметическая отклонения вариантов от средней арифметической равна нулю:
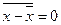 .
.
5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:
 .
.
6. Если ряд состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем, весами являются объемы групп:
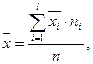
где 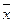 - общая средняя (средняя арифметическая всего ряда);
- общая средняя (средняя арифметическая всего ряда); 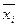 - групповая средняя
- групповая средняя 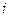 - ой группы, объем которой равен
- ой группы, объем которой равен 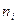 ;
; 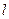 - число групп.
- число групп.
Кроме рассмотренных средних величин, называемых аналитическими, в статистическом анализе применяют структурные, или порядковые, средние. Из них наиболее широко применяются медиана и мода.
Опр. Медиана 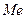 - это значение, которое делит упорядоченное множество данных пополам, или медиана – это центральное значение упорядоченного ряда вариант.
- это значение, которое делит упорядоченное множество данных пополам, или медиана – это центральное значение упорядоченного ряда вариант.
· Если данные содержат нечетное число значений, то медиана – это центральное значение в упорядоченном ряду.
· Если данные содержат четное число значений, то медиана равна полусумме двух серединных вариантов.
· Для интервального вариационного ряда находится медианный интервал, на который приходится середина ряда, а значение медианы на этом интервале находят с помощью линейного интерполирования.
Замечание. Медиана может быть приближенно найдена с помощью кумуляты как значение признака, для которого 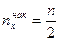 или
или 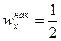 .
.
Достоинство медианы как меры центральной тенденции заключается в том, что на нее не влияет изменение крайних членов вариационного ряда, если любой из них, меньший медианы, остается меньше ее, а любой, больший медианы, продолжает быть больше ее. Медиана предпочтительнее средней арифметической для ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми.
Опр. Мода  - это значение, которое встречается в выборке наиболее часто.
- это значение, которое встречается в выборке наиболее часто.
· В случае, когда все значения встречаются одинаково часто, принято считать, что выборка не имеет моды.
· Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений.
· Если два не соседних (несмежных) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. Говорят, что выборка бимодальная.
Замечание. Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод).
· Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной.
· Для интервального ряда находится модальный интервал, имеющий наибольшую частоту, а значение моды на этом интервале определяют с помощью линейного интерполирования. Но проще найти графическим путем с помощью гистограммы.
Особенность моды как меры центральной тенденции заключается в том. Что она не изменяется при изменении крайних членов ряда, т.е. обладает определенной устойчивостью к вариации признака.
Показатели вариации
Заметим, что средние величины не отражают изменчивости (вариации) значений признака.
Простейшим показателем вариации является вариационный размах:  , где
, где  - наибольшая варианта,
- наибольшая варианта,  - наименьшая варианта.
- наименьшая варианта.
Опр. Средним линейным отклонением вариационного ряда называется средняя арифметическая абсолютных величин отклонений вариантов от их средней арифметической:
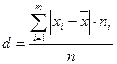 . (8)
. (8)
Опр. Дисперсией 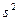 вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:
вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:
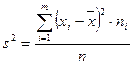 , (9)
, (9)
или
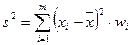 , (10)
, (10)
где 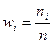 .
.
Если ряд сгруппирован, т.е. 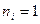 , то
, то
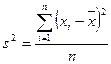 . (11)
. (11)
Дисперсию 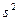 часто называют эмпирической или выборочной, подчеркивая, что она находится по опытным или статистическим данным.
часто называют эмпирической или выборочной, подчеркивая, что она находится по опытным или статистическим данным.
Опр. Среднее квадратическое отклонение 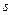 - арифметическое значение корня квадратного из дисперсии:
- арифметическое значение корня квадратного из дисперсии:
 . (12)
. (12)
Среднее квадратическое отклонение является характеристикой, которая выражена в тех же единицах измерения, что и сам признак.
Опр. Коэффициент вариации – это безразмерная характеристика, вычисляемая по формуле:
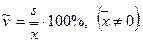 (13)
(13)
Замечание. Если коэффициент вариации признака, принимающего только положительные значения, высок 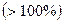 , то, как правило, это свидетельствует о неоднородности значений признака.
, то, как правило, это свидетельствует о неоднородности значений признака.
Свойства дисперсии
1. Дисперсия постоянной равна нулю.
2. Если все варианты увеличить (уменьшить) в одно и то же число  раз, то дисперсия увеличится (уменьшится) в
раз, то дисперсия увеличится (уменьшится) в  раз.
раз.
3. Если все варианты увеличить (уменьшить) на одно и то же число, то дисперсия не изменится.
4. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической:
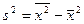 , (14)
, (14)
где
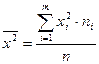 . (15)
. (15)
5. Если ряд состоит из нескольких групп наблюдений, то общая дисперсия равна сумме средней арифметической групповых дисперсий и межгрупповой дисперсии:
 , (16)
, (16)
где 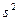 - общая дисперсия (дисперсия всего ряда);
- общая дисперсия (дисперсия всего ряда);  (17) - средняя арифметическая групповых дисперсий;
(17) - средняя арифметическая групповых дисперсий; 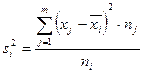 (18);
(18);  (19) – межгрупповая дисперсия.
(19) – межгрупповая дисперсия.
Формулу (16) называют «правилом сложения».
Дата добавления: 2022-01-22; просмотров: 18; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
