Вероятность произведения событий.
Лекция 1. Основные понятия теории вероятности. (ТВ)- СС-1
ТВ – это раздел математики изучающий закономерности случайных явлений. «ТВ объединяет точность математических доказательств с неопределённостью случая и примеряет эти противоречивые элементы».
Случайное явление - явление с неопределённым исходом, который при неоднократном воспроизведении некоторого комплекса условий происходит несколько по разному.
Существует два подхода к изучению таких явлений: 1). Детерминистский. 2). Вероятностный.
Испытание - модель реального действия. реализация определённого комплекса условий который может быть воспроизведён сколько угодно раз. Задать испытание в т/в это значит задать множество его элементарных (неделимых на более мелкие) исходов W. W= 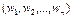 .
.
Случайное событие - событие которое может наступить или не наступить в результате испытания. Для любого события “А” множество W элементарных событий разделяется на два подмножества W – А+ и А– .
А+ - подмножество благоприятных исходов вместе с каждым из которых наступает событие А+.
А– - подмножество неблагоприятных исходов, при реализации которых событие А не происходит.
Задать событие– это значит задать подмножество А+ благоприятных исходов на множестве W.
Невозможное событие - событие которое никогда ни происходит в результате испытания. Достоверное событие - событие которое всегда происходит при испытании.
|
|
|
Два события называются несовместными, если появление одного исключает появление другого.
События совместны, если они могут произойти одновременно.
Вероятность случайного события- это количественная мера степени уверенности в его наступлении.
Классическое определение вероятности: Для испытания с конечным числом равновозможных исходов вероятность случайного события “A” обозначается Р(А) и определяется как отношение числа благоприятных исходов m к общему числу n элементарных исходов испытания:
Р(А) = m / n .
Вероятность случайного события принимает значения от 0 до 1. 0 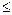 Р(А)
Р(А) 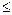 1
1
Вероятность невозможного события равна 0. Вероятность достоверного события равна 1.
Статистическое определение вероятности. Относительная частота события А -отношение числа наступления события А в серии изn испытаний к общему числу испытаний (n). m (А)/ n .
Если в различных сериях из n испытаний относительная частота события мало изменяется и близка некоторому числу Р , то это число считают статистической вероятностью.
Геометрическое определение вероятности - Применяется к опыту (испытанию) с бесконечным числом равновозможных исходов. Пусть дан отрезок длины “L” и на нём отрезок “L1” Под геометрической вероятностью принимается вероятность попадания точки на отрезок L1, равная отношению длин этих отрезков Р(А) = L1/L
|
|
|
| |
Комбинаторика – это раздел математики в которой изучаются расположения (комбинации) объектов составленные по определённым правилам и способам подсчёта этих комбинаций.
Основными расположениями объектов являются: перестановки размещения и сочетания.
Основное правило комбинаторики: если элемент а1 можно выбрать “n1” способами и при каждом таком выборе, выбор элемента а2 может быть произведён n2 способами, то общее число пар (а1;а2) равно N = n1۰n2.
Перестановками называют упорядоченное множество составленное из всех элементов “A”. Перестановки отличаются друг от друга порядком элементов.
Рn – число перестановок множества из n элементов = n۰(n – 1)۰(n – 2)…1 = n!; (0! = 1; 1! = 1; 2! = 2; 3! = 6…).
Размещения. Ank упорядоченные k- элементные подмножества n элементного множества.
Число размещений : Ank=n(n-1)(n-2)۰…۰(n – k + 1)= 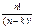
Сочетания Cnk -“k” элементные подмножества “n” элементного множества. Два сочетания отличаются друг от друга только составом элементов, но не их порядком.
|
|
|
Связь между числом сочетаний , размещений и перестановок. Ank = Cnk۰Pk
Число сочетаний: Cnk =Ank/Pk = 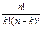 Свойства числа сочетаний: 1). Cnk = Cnn – k; 2). Cnk = Cn – 1 k – 1 + C k n – 1
Свойства числа сочетаний: 1). Cnk = Cnn – k; 2). Cnk = Cn – 1 k – 1 + C k n – 1
Лекция 2. Основные теоремы теории вероятности. СС-2
События “A” и “B” связанные с одним и тем же испытанием, называются эквивалентными, если их множества благоприятных исходов А+ и В+ совпадают. Вероятности эквивалентных событий равны Р(А) = Р(В).
– Операции над событиями –
Противоположным событием для события “A” называется новое событие - 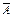 , состоящее в том, что событие “A” не произошло. (Событие
, состоящее в том, что событие “A” не произошло. (Событие 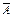 происходит тогда и только тогда, когда не происходит событие А).
происходит тогда и только тогда, когда не происходит событие А).
Суммой или объединением двух событий А и В называется новое событие С=А+В =А  В, которое состоит в том, что произошло хотя бы одно из этих событий (или событие А, или В или А и В одновременно). Если события А и В несовместные, то сумма А+В заключается в появлении одного из них.
В, которое состоит в том, что произошло хотя бы одно из этих событий (или событие А, или В или А и В одновременно). Если события А и В несовместные, то сумма А+В заключается в появлении одного из них.
Произведением или пересечением двух событий А и В называется новое событие С=А۰В =А∩В, заключающееся в одновременном наступлении событий А и В.
– Свойства операций над событиями –
1). Коммутативность сложения А + В = В + А. 2). Ассоциативность сложения (А + В) + С = А + (В + С).
|
|
|
3). Коммутативность умножения А۰В = В۰А. 4). Ассоциативность умножения (А۰В)С = А(В۰С).
5). Сумма противоположных событий – достоверное событие. 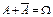
6). Произведение противоположных событий, есть невозможное событие. 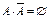
Вероятность произведения событий.
Условной вероятностью РВ(А) события А называется- - вероятность появления события А, при условии, что событие В уже произошло.
События А и В независимы, если Р(А)=РВ(А) и Р(В)=РА(В).
Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого 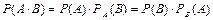 .
.
Вероятность произведения двух независимых событий равна произведению их вероятностей 
Условная вероятность РВ(А) равна отношению вероятности совместного наступления событий А и В к вероятности события В. 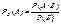
.– Теоремы сложения вероятностей –
Теорема сложения вероятностей несовместных событий. Вероятность суммы несовместных событий равна сумме их вероятностей.
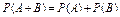 - вероятность суммы несовместных событий
- вероятность суммы несовместных событий
Доказательство проведём для испытания с конечным числом n равновозможных исходов. Пусть
m1 – число исходов благоприятствующих событию A, а m2 – число исходов благоприятствующих событию В. Тогда вероятность события А = m1/n; а Р(В)= m2/n. Т.к. эти события несовместные, то число исходов благоприятствующих событию А + В = m1 + m2, тогда Р(А + В) = (m1 + m2)/n = m1/n + m2/n = Р(А) + Р(В).
Следствие 1: Вероятность суммы нескольких попарно несовместных событий = сумме их вероятностей Р() = Р(А1) + Р(А2) +…+ Р(Аn)
События А1,А2 , …, Аn образуют полную группу, если они попарно несовместны и в результате испытания обязательно произойдёт хотя бы одно из них.
Следствие 2: Сумма вероятностей событий, образующих полную группу, равна 1.
Следствие 3. Сумма вероятностей противоположных событий равна 1. 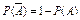
Общая теорема сложения вероятностей Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Р(А+В) = Р(А) + Р(В) - Р(АВ) – вероятность суммы совместных событий.
Доказательство: из опр. суммы возможны три несовместных варианта: А и В произошли вместе - А۰В , произошло А, но не В – 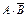 , произошло только В -
, произошло только В - 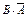 . Для независимых событий вероятность первого варианта –
. Для независимых событий вероятность первого варианта –  , вероятн. второго Р(
, вероятн. второго Р( 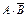 )=
)=  ; Р(
; Р( 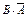 ) =
) = 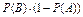 - вер. третьего. Сложив эти вероятности, получим вероятность суммы совместных независимыхсобытий
- вер. третьего. Сложив эти вероятности, получим вероятность суммы совместных независимыхсобытий
Лекция 3-4. Основные теоремы теории вероятности. СС-3
Формула полной вероятности.
Пусть появление некоторого события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами.
Тогда вероятность события А равна сумме попарных произведений вероятности каждой из этих гипотез Вi на соответствующую условную вероятность появления события А.
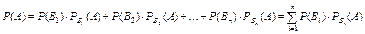
Формулы Байеса.
Пусть появление в некотором испытании события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами.
Тогда, зная вероятности гипотез Р(Вi) до проведения испытания, мы можем переоценить их после проведения испытания, в результате которого появилось событие А.
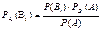 ,
,
где  - вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло (апостериорные вероятности гипотез); Р(А) – полная вероятность события А,
- вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло (апостериорные вероятности гипотез); Р(А) – полная вероятность события А,
Р(Вi) – вероятности гипотез, известные до испытания (априорные вероятности гипотез),
 — вероятность наступления события А при истинности гипотезы Вi.
— вероятность наступления события А при истинности гипотезы Вi.
Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. По формуле Байеса можно более точно пересчитывать вероятность, принимая во внимание как ранее известную информацию (априорные данные), так и данные новых наблюдений (апостериорные данные).
Вычисление вероятностей событий в серии независимых испытаний.
Схема Бернулли - последовательность независимых испытаний (т.е. таких испытаний, вероятность исходов которых не зависит ни от номера испытания, ни от результатов предшествующих испытаний) с двумя возможными исходами. Вероятность первого исхода - А, называемого успехом, в каждом испытаний равна р, тогда вероятность второго исхода – неуспеха, равна разности единицы и р : Р(А)=р Р( 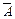 )=1-р= q .
)=1-р= q .
Формула Бернулли
Вероятность, что в серии из n испытаний по схеме Бернулли ,событие А, произойдёт ровно k раз:
 , где
, где 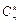 число сочетаний из “n” элементов по “k” элементов в каждом.
число сочетаний из “n” элементов по “k” элементов в каждом.
р – вероятность наступления события А в одном испытании, 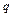 –вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний.
–вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний.
Теорема Лапласа: применяется при больших значениях n , когда формулу Бернулли использовать сложно.
Пусть Р(А)=р – вероятность проявления события А в одном испытании,
тогда вероятность, что в серии из n независимых испытаний событие А произойдёт точно k раз приблизительно вычисляется по формуле Лапласа:
 , где
, где 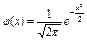 ; где
; где 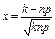 ,
, 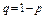 .
.
Интегральная теорема Лапласа. – позволяет определить вероятность того, что событие А в n независимых испытаниях произойдёт не менее 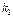 и не более
и не более  раз.
раз.
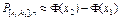 , где
, где 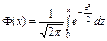 ,
, 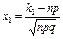 ;
; 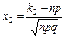
Значения функций  и
и 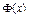 приводятся в таблицах (см тб. 1 и 2)
приводятся в таблицах (см тб. 1 и 2)
Закон Пуассона распределения вероятностей массовых и редких событий.
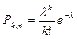 -вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз.
-вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз.
где 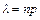 , n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании.
, n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании.
Формула Пуассона применяется, когда n – очень велико, а р – достаточно мало.
Дата добавления: 2022-01-22; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
