Системна функція (передавальна функція) дискретного фільтру.

Лекція № 7.

РОЗДІЛ 5 Дискретні сигнали та методи їх аналізу

Тема 7. Дискретні сигнали та методи їх аналізу

Моделі дискретних сигналів. Дискретизація періодичних сигналів, дискретне перетворення Фур'є. Обернене дискретне перетворення Фур'є. Властивості дискретного перетворення Фур’є. Швидке перетворення Фур'є та його алгоритм. Дискретна згортка.

Пряме та обернене z-перетворення, його властивості.

Моделі дискретних сигналів. Дискретизація періодичних сигналів . Дискретне перетворення Фур'є

Дискретне перетворення Фур'є (ДПФ) відноситься до класу основних перетворень при цифровій обробці сигналів. Дискретне перетворення Фур'є, яке частіш за все обчислюється швидкими методами, лежить в основі різних технологій спектрального аналізу.

При дискретизації аналогового сигналу його спектр стає періодичним з періодом повторення, рівним частоті дискретизації . З іншого боку, дискретному спектру повинен відповідати періодичний сигнал.

Розглянемо як початкові дані послідовність 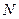дискретних відліків 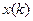, заданих на відрізку , 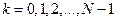. Моделлю послідовності таких відліків є сигнал із зміщених за часом дельта-функцій:

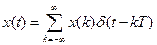. (7.1)

Продовжимо подумки цей сигнал з періодом 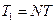. Оскільки дискретний сигнал (7.1) - періодичний, його спектр має бути дискретним з відстанню між гармоніками, рівними 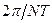. Цей дискретний періодичний сигнал можна представити рядом Фур'є

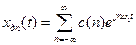. (7.2)

Коефіцієнти цього ряду знаходять згідно з формулою

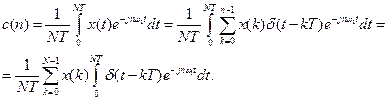(7.3)

Якщо перейти до нової змінної t ’=t/T, отримаємо

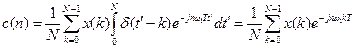. (7.4)

Оскільки , остаточно маємо

(7.5)

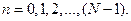
Співвідношення (7.5), що дозволяє обчислити комплексні амплітуди гармонік дискретного сигналу, є лінійною комбінацією відліків цього сигналу. Його називають прямимдискретним перетворенням Фур'є (ДПФ).

Разом з прямим ДПФ існує і обернене (обернене) дискретне перетворення Фур'є

(7.6)

Зауваження. У розміщенні множника 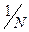у виразі (7.5) немає повної єдності. У деяких джерелах цей множник відносять до формули оберненого (оберненого) ДПФ, видаляючи його з формули для прямого ДПФ.

Ортогональний дискретний базис Фур'є, в якому виконується ДПФ, є системою дискретних експоненціальних функцій (ДЕФ), заданою на дискретній часовій осі N відліками, :

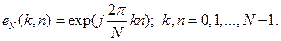(7.7)

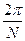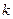Система функцій (7.7) є набором N експонент з частотами, кратними основній частоті , оскільки періодична по з періодом .

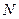Властивості дискретного перетворення Фур'є.

1. Лінійність.

Дискретне перетворення Фур'є - лінійне перетворення, тобто якщо послідовностям 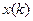і з одним і тим же періодом 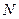відповідають набори гармонік і 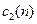, то послідовності 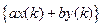відповідатиме спектр .

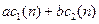2. Симетрія.

Властивість симетрії, якою володіє спектр безперервного сигналу, зберігається і для спектру дискретного періодичного сигналу. Якщо відліки 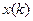- дійсні числа, тоді коефіцієнти ДПФ, номери яких розташовані симетрично відносно 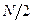, утворюють спряжені пари:

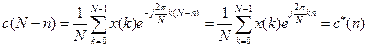. (7.8)

З формули (7.8) виходить, що спектр є спряжено симетричним відносно 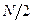, тобто містить рівно таку ж кількість інформації, що і сам сигнал. Дійсно, якщо початковий сигнал представляється набором з 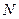дійсних чисел, то його спектр представляється набором з 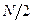комплексних чисел, кожне з яких з інформаційної точки зору еквівалентне двом дійсним. Друга половина спектру взаємно-однозначно пов'язана з першою. Можна вважати, що коефіцієнти 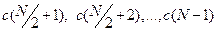відповідають від’ємним частотам. При вивченні амплітудного спектру сигналу вони не дають нової інформації.

Гармоніка з нульовим номером (постійна складова), як випливає з (7.5), є середнім значенням усіх відліків сигналу на одному періоді

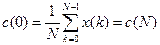. (7.9)

Якщо 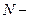парне число, тоді

(7.10)

І амплітуда гармоніки з номером 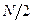визначається сумою відліків зі знаками, що чергуються, .

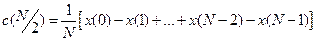3. ДПФ кругової згортки.

Візьмемо дві послідовності і 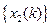однакової довжини 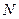, ДПФ яких відповідно рівні і 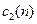. Обчислимо їх кругову згортку по одному періоду

. (7.11)

Знайдемо 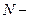точкове ДПФ цієї згортки

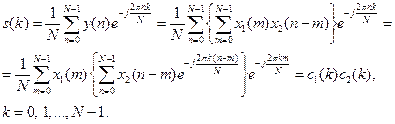(7.12)

При виведенні формули (7.12) врахована властивість зсуву періодичної послідовності. Таким чином, круговій згортці дискретизованих сигналів заданих на одному часовому проміжку відповідає перемножування їх спектрів.

Обчислення кругової згортки двох сигналів за допомогою ДПФ здійснюється за наступним алгоритмом:

· обчислення ДПФ вихідних сигналів за формулою (7.5);

· перемножування коефіцієнтів отриманих ДПФ згідно (7.12);

· обчислення сигналу 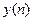за допомогою оберненого ДПФ отриманої послідовності .

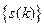4. Рівність Парсеваля для дискретних сигналів.

Визначимо значення 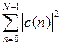, використовуючи формулу ДПФ

(7.13)

При виведенні формули (7.13) використана умова ортогональності дискретних експоненціальних функцій

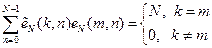. (7.14)

Таким чином, потужність сигналу 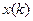на 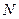відліках дорівнює сумі потужностей його частотних компонентів.

5. Зв'язок ДПФ і спектру дискретного сигналу.

Маючи один і той же набір значень дискретного сигналу 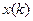, можна розрахувати або спектральну функцію 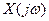цього дискретного сигналу по формулі , або його ДПФ по формулі (7.5). Порівняння цих формул показує, що ДПФ є просто дискретними відліками спектральної функції дискретного сигналу, які відповідають частотам :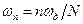

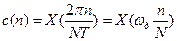. (7.15)

Із співвідношення (7.15) маємо важливий висновок: якщо додати до кінцевого набору відліків деяку кількість нулів, спектральна функція дискретного сигналу, природно, не зміниться, але ДПФ дасть більше число спектральних відліків, які відповідатимуть частотам більш щільно розташованим в інтервалі від нуля до частоти дискретизації.

6. Обчислення оберненого ДПФ за допомогою прямого ДПФ.

Для обчислення оберненого ФПФ можна без будь-яких змін застосовувати пряме ДПФ. Обернене ДПФ N-точкової послідовності 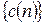, визначається наступним чином Якщо взяти комплексне спряження від цього виразу та поділити його на N матимемо

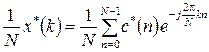. (7.16)

Права частина цього виразу є ДПФ послідовності , яке може бути обчислене з використанням одного з алгоритмів обчислення прямого ДПФ (наприклад, одного з ШПФ). Шукану послідовність можна отримати, взявши комплексно спряжений з (7.16) вираз і помножити його на N, а саме

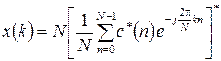Далі будемо користуватися більш поширеним представленням прямого та оберненого перетворення Фур'є, коли множник 1/ N застосовується у співвідношенні для обчислення оберненого перетворення Фур'є.

Швидке перетворення Фур'є

Знаходження спектральних складових 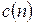дискретного комплексного сигналу 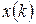безпосередньо по формулі ДПФ вимагає 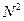комплексних множень і 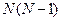комплексних додавань. Оскільки кількість обчислень, а отже, і час обчислень приблизно пропорційні 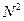, то при великих 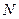кількість арифметичних операцій дуже велика. Тому знаходження спектру в реальному часі навіть для сучасної обчислювальної техніки є складним завданням.

З цієї причини представляють значний інтерес обчислювальні процедури, які зменшують кількість множень і складань. Основний принцип усіх цих алгоритмів полягає в розкладанні операцій обчислення ДПФ сигналу довжини 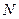на обчислення перетворень Фур'є з меншим числом точок. Розділивши аналізований набір відліків на частини, обчислюють їх ДПФ і об'єднують результати. Такі процедури дістали назву алгоритмів швидкого перетворення Фур'є (ШПФ).

При реалізації ШПФ можливі декілька варіантів організації обчислень залежно від способу ділення послідовності відліків на частини (проріджування за часом або по частоті) і від того, на скільки фрагментів розбивається послідовність на кожному кроці (основа ШПФ). Найбільш простими і широко використовуваними є алгоритми ШПФ з основою 2, коли довжина послідовності 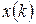є цілою мірою числа 2, тобто , де 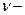ціле число.

Проаналізуємо більш детально операції ДПФ на прикладі N=8. У цьому випадку, ввівши загальноприйняте в літературі позначення для дискретних експоненціальних функцій

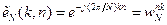, (7.17)

матимемо 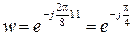, тут і далі індекс N=8 опущено для простоти запису.

Користуючись матричним представленням вираз для обчислення ДПФ (вже без множника 1/ N)

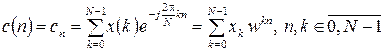, (7.18)

може бути представлений у вигляді добутку

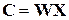, (7.19)

де матриця ДПФ прийме вигляд

, (7.20)

і вектор , - знак транспонування.

Проаналізуємо 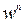. Точки 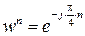знаходяться на колі одиничного радіусу і являють собою періодичну послідовність. Тобто значення 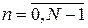повністю визначають будь-яку степінь при (за умови N=8).

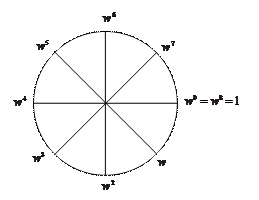Рисунок 7.1 – Комплексна площина .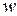

Показані числа = .

Суми виду (7.18) називають згортками. Згортки, які мають вказану властивість називають круговими.

Звернемо також увагу на те, що числа, які відповідають точкам розташованим діаметрально протилежно на колі відрізняються лише знаком. Тому 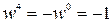, , 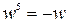, 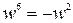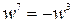. Тобто будь-яка ціла степінь 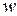може бути представлена через 1, 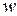, , 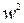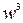. З урахуванням цього матрицю ДПФ можна подати у вигляді

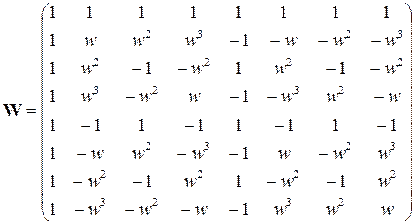. (7.21)

В кожній строчці цієї матриці можна побачити або однакові або такі, що різняться за знаком члени. Ідея ШПФ застосовує описані вище властивості кругової згортки і, крім того, передбачає скорочення кількості операцій множення відповідно до тотожності

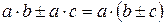. (7.22)

Ліворуч у виразі (7.22) два множення, а праворуч лише одне. З урахуванням цього знайдемо складові дискретного спектру:

;

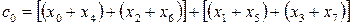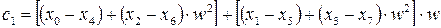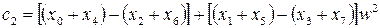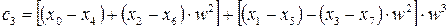; (7.23)

;

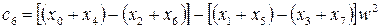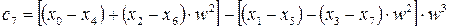Видно, що у круглих дужках маються лінійні комбінації елементів вектора . Кількість таких комбінацій дорівнює 8. В квадратних дужках вагові комбінації сум у круглих дужках (їх теж вісім). Останні операції передбачають утворення вагових сум з результатів у квадратних дужках.

Ці три послідовні етапи обчислення можуть бути представлені у вигляді добутку трьох порівняно простих матриць (відповідно з права на ліво). Таким чином, матриця ДПФ приймає вигляд

, (7.24)

де

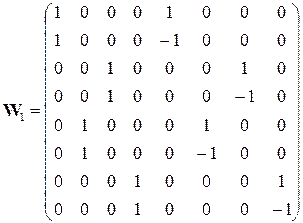, (7.25)

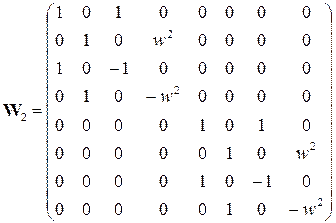, (7.26)

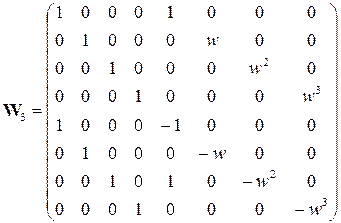. (7.26)

Якщо обчислити добуток цих трьох матриць отримаємо матрицю . Розкладання матриць на прості множники виду (7.24) називають факторизацією.

Процедуру обчислення дискретного спектру зручно подати у вигляді графа (рис. 7.2), який пояснює послідовність дій, виконуваних факторизованою матрицею.

Рисунок 7.2 – Граф ШПФ. Кружком позначено підсумовування, а квадратом - множення на величину, що вказана в квадраті.

Промисловість серійно випускає інтегральні мікросхеми, які виконують чотирьохточкове ДПФ, яке є базовою операцією. Цю мікросхему називають «метеликом». Вона дозволяє виготовляти спеціалізовані процесори ШПФ для сигналів з довільним N.

Алгоритмічна схема «метелика» і її позначення наведені на рис. 7.3. Якщо на її вхід поступають комплексні числа 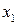і 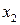, тоді на на виході формуються числа згідно з виразами x₁ + x₂wⁿ і x₁ - x₂wⁿ . Оскільки комплексні величини являють собою пару чисел (реальні і мнимі частини), тому практично «метелик» має чотири входи і чотири виходи.

Рисунок 7.3 – Алгоритмічна схема і умовне позначення «метелика»

Як видно зі структурної схеми восьмиточечного спецпроцесора ШПФ реалізованого на «метеликах» (рис. 7.4), в ній реалізовані операції предписані факторизованою матрицею (7.24).

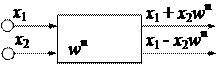Рисунок 7.4 – Структурна схема спецпроцесора ШПФ на «метеликах»

Формально ШПФ здійснюється шляхом розбивання вихідної послідовності на парні 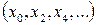і непарні 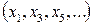підпослідовності. З ними далі подібним же чином. Ці процедури повторюються доти, поки не залишиться по одній парі чисел, які поступають на «метелики» першого етапу. Стосовно до восьми точкового ШПФ цими парами є , , 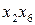, 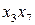. На першому етапі операцій множення практично не проводиться (множення на 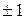). Тут формуються суми і різниці отриманих пар.

Далі алгоритм обчислення відповідає рис. 7.4. Видно, що вся операція складається з трьох етапів. В загальному випадку для N -точкового ШПФ потрібно етапів. На кожному з них виконується N/2 операцій множення. Таким чином, алгоритм ШПФ потребує 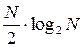операцій множення. Загальний алгоритм ДПФ має операцій множення. Тому алгоритм ШПФ порівняно з алгоритмом ДПФ дає виграш по кількості операцій множення в 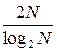разів.

3. Пряме та обернене Z -перетворення, його властивості. Дискретна згортка

Z -п е ре тв ор ен н я .

Зручним способом аналізу дискретних послідовностей є Z-перетворення. При Z-перетворенні різницеві рівняння, що описують роботу дискретної системи, перетворюються в рівняння алгебраїчні, з якими простіше виконувати необхідні дії. Z-перетворення відіграє для дискретних сигналів і систем таку ж роль, як перетворення Лапласа - для аналогових сигналів.

Визначення Z -преобразования. Дискретній послідовності відліків 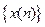ставиться у відповідність функція комплексної змінної z, яка визначається таким чином,

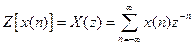(7.27)

Функція 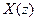визначена тільки для тих значень z, при яких ряд (7.27) сходиться. Якщо послідовність 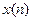має обмежену довжину, то 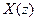сходиться в Z-площині скрізь, за виключенням, можливо, точок z = 0 або z = .

Отримаємо Z-перетворення для деяких дискретних сигналів, що часто зустрічаються на практиці.

Одиничний імпульс, який визначається як

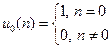. (7.28)

Використовуючи формулу (7.27), отримаємо:

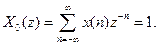(7.29)

Функція 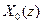сходиться в усій комплексній площині.

Одиничний стрибок, який визначається як

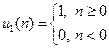. (7.30)

Використовуючи визначення Z-перетворення, отримуємо

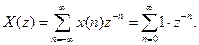(7.31)

Ряд (7.31) є сумою нескінченної геометричної прогресії з першим членом 1 і знаменником . Як відомо, такий ряд сходиться при 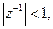тобто при 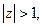і його сума складає

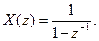(7.32)

Значення є єдиною особливою точкою (полюсом) функції .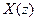

Експоненціальна дискретна функція

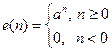. (7.33)

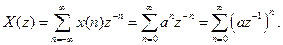(7.34)

Як і у попередньому випадку, цей ряд є сумою геометричної прогресії з першим членом, рівним 1 і знаменником . Таким чином, ряд сходиться при 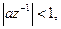тобто при 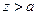, і має особливу точку при :

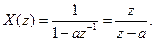(7.35)

Комплексна дискретна експонента, яка визначена співідношенням

. (7.36)

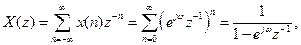(7.37)

причому 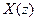сходиться при 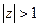, оскільки єдиною особливою точкою 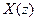є .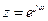

Зв'язок Z–перетворенняз перетворенням Лапласа знайдемо, записавши аналоговий сигнал у вигляді суми дискретних відліків і набору дельта-функцій

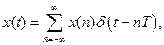(7.38)

де 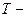крок дискретизації. Перетворення Лапласа для такого сигналу дорівнює

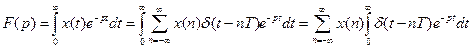. (7.39)

Скориставшись фільтрувальною властивістю дельта-функції, отримаємо

(7.40)

Порівнюючи співвідношення (7.27) і (7.40), помічаємо, що одна формула переходить в іншу при заміні 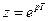. Таким чином, Z-перетворення можна отримати з перетворення Лапласа шляхом переходу до нової змінної:

(7.41)

Сенс використання Z-преобразования при аналізі дискретних сигналів витікає з наступного. Оскільки справедливе співвідношення

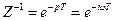, (7.42)

тоді зміна фазової характеристики сигналу означає затримку сигналу на один крок дискретизації 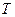і відповідає затримці сигналу на один такт в області.

Перехід від перетворення Лапласа до Z-перетворення при описанні дискретних систем потрібний з наступної причини. Дискретизація аналогового сигналу призводить до періодичності частотного спектру, тобто появи нескінченного ряду зсунутих копій спектру початкового безперервного сигналу. Очевидно, ефект дискретизації призводить до появи в площині нескінченної конфігурації особливих точок (полюсів і нулів).

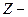При переході від площини до площини точка 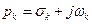відображується в точку 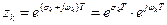. Тому шлях уздовж уявної осі 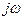в площині відображується в одиничне коло в 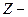площині, оскільки на уявній осі і, отже 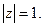Можна показати, що ліва (стійка) смуга площини шириною відображується всередину кола одиничного радіусу 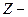площини. Усі наступні смуги площини шириною , відповідні періодичному частотному спектру дискретного сигналу, також відображуються всередину круга одиничного радіусу 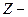площини. Тому конфігурація особливих точок (полюсів і нулів) в 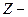площині стає кінцевою.

Таким чином, взаємна відповідність між Z-перетворенням 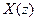та перетворенням Лапласа 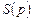описується наступним чином:

; .

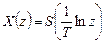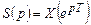Подібними формулами описується зв’язок Z-перетворення 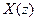з перетворенням Фур’є 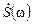(при цьому немає необхідності вважати послідовність однобічною):

; .

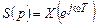Зв'язок ДПФ з Z -перетворенням.

Порівнюючи формулу прямого ДПФ дискретної послідовності 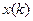з формулою Z-перетворення, побачимо, що коефіцієнти ДПФ дорівнюють значенням Z-перетворення цього сигналу в 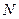точках, рівномірно розподілених по одиничному колу Z-площини. Ці коефіцієнти однозначно представляють саму послідовність, оскільки вона може бути точно відновлена за допомогою оберненого ДПФ.

Отримаємо Z-перетворення послідовності через коефіцієнти ДПФ цієї послідовності

. (7.43)

Формула (7.43) показує, що Z-перетворення кінцевої послідовності 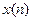, 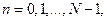безпосередньо пов'язано з коефіцієнтами , , її ДПФ.

Властивості Z -перетворення

1. Лінійність.

Якщо 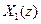і 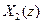є Z-перетвореннями відповідних сигналів і 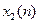, тоді сигналу 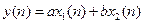відповідатиме Z-перетворення 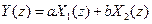при будь-яких постійних 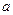і

2. Затримка (зсув послідовності).

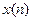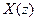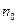Якщо Z-перетворення сигналу дорівнює , тоді Z-перетворення сигналу , затриманого на тактів, буде рівне .

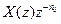Д оведення .

. (7.44)

Таким чином, при затримці сигналу на 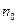тактів необхідно помножити його Z-перетворення на множник .

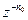Зокрема, якщо сигнал отриманий шляхом зсуву сигналу 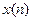на один такт у бік запізнювання, тоді його Z-перетворення . Отже, символ слугує оператором одиничної затримки (на один інтервал дискретизації) в області.

3. Згортка.

Введемо дискретну лінійну згортку 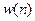, яку визначимо таким чином:

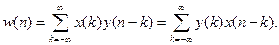(7.45)

Обчислимо її Z-перетворення:

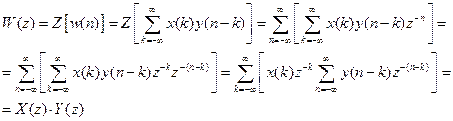. (7.46)

Отже, Z-перетворення лінійної згортки двох дискретних сигналів дорівнює добутку їх Z-перетворень.

Системна функція (передавальна функція) дискретного фільтру.

Застосуємо третю властивість Z-перетворення до рівняння дискретної фільтрації: 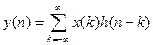. Оскільки вихідний сигнал дискретної системи є лінійною згорткою вхідного сигналу з імпульсною характеристикою системи, тоді

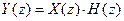, (7.47)

де - Z-перетворення відповідно вхідного і вихідного сигналів системи, а – Z-перетворення її імпульсної характеристики

. (7.48)

Враховуючи, що дорівнює відношенню двох перетворених сигналів (вихідного і вхідного), її називають системною або передавальною функцією. Вона грає найважливішу роль в побудові дискретних цифрових систем.

Застосуємо Z-перетворення до обох частин різницевого рівняння

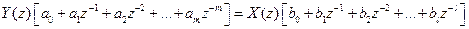(7.49)

і звідси отримуємо загальний вигляд передавальної функції :

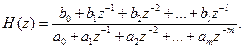(7.50)

Таким чином, передавальна (системна) функція дискретної системи, що фізично реалізується, може бути представлена у вигляді відношення поліномів по від’ємних степенях змінної z.

Импульсной характеристикой дискретного фильтра называется его реакция на единичный импульс 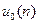при нулевых начальных условиях:

или (1)

где 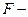оператор преобразования дискретного фильтра. Импульсную характеристику фильтра 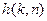обычно представляют совокупностью значений 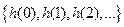, называемых коэффициентами фильтра.

Заметим, что любую дискретную последовательность 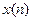можно представить в виде линейной комбинации единичных отсчетов:

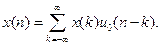(2)

Тогда выходной сигнал, исходя из линейности и стационарности рассматриваемой системы, должен представлять собой линейную комбинацию импульсных характеристик:

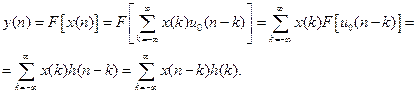(3)

Выражение (8.3) представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра. Если фильтр физически реализуем (каузален), то его реакция на выходе не может появиться раньше воздействия на его входе (принцип временного детерминизма). Следовательно, его импульсная характеристика должна равняться нулю в отсчетных точках, предшествующих моменту подачи входного импульса, т.е. 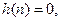при 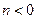. Поэтому верхний предел суммирования в формуле (3) может быть заменен на :

(4)

Оскільки системна функція є Z-перетворенням від імпульсної характеристики системи , порівняємо це співвідношення з виразом для частотного коефіцієнта передачі, який також може виражатися через значення імпульсної характеристики відповідно .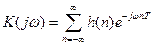

Очевидно, щоб отримати частотний коефіцієнт передач (частотну характеристику) дискретної системи з його системної функції, в останній треба зробити підстановку: .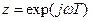

Таким чином, маючи різницеве рівняння або структурну схему дискретної системи, не складно визначити її системну функцію і частотний коефіцієнт передачі.

Приклад . Визначити системну функцію рекурсивного фільтру другого порядку.

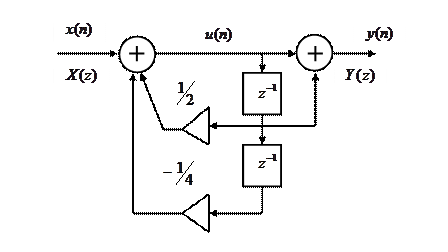
Рішення. Введемо для аналізу проміжний сигнал і запишемо рівняння відносно двох суматорів у формі різницевих рівнянь:

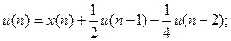(7.51)

(7.52)

Застосовуючи Z –перетворення до рівнянь (7.51) і (7.52), отримуємо:

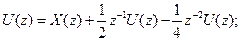
Отже,

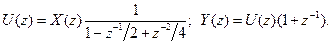(7.53)

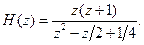
Різницеві рівняння зазвичай визначені при 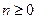і мають набір початкових умов. Тому при рішенні практичних задач зазвичай вводять одностороннє Z-перетворення, що має вигляд

. (7.54)

Для багатьох сигналів властивості одностороннього Z-перетворення аналогічні властивостям звичайного Z-перетворення. Основним виключенням є властивість, пов'язана із зсувом (затримкою) сигналів. Так, затримка на один відлік як і раніше призводить до множення одностороннього Z–перетворення на , але при цьому необхідно врахувати значення сигналу 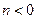, тобто початкові умови.

Обернене Z -перетворення.

Відповідно до (7.54) функція 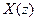визначає усю нескінченну сукупність відліків . Помножимо обидві частини ряду (7.54) на множник :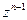

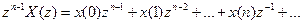, (7.55)

а потім обчислимо інтеграли від обох частин отриманої рівності, взявши за контур інтегрування замкнуту криву, що лежить цілком в області аналітичності і охоплює усі полюси функції 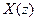. При цьому скористаємося теоремою Коши

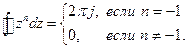
Очевидно, інтеграли від усіх доданків правої частини перетворяться на нуль, за винятком доданку з номером . Тому

, (7.56)

де 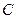- замкнутий контур колом 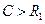, 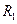- радіус збіжності .

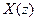Вираз (7.56) називають оберненим Z -перетворенням, воно дозволяє знайти відліки 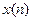по Z -зображеннию 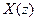. Обернене Z–перетворення існує тільки для таких функцій 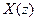, які мають лише кінцеве число особливих точок (полюсів), причому особливість в кожній з них є усувною.

Існує декілька методів обчислення оберненого Z-перетворення. Найчастіше користуються теоремою про вирахування (вычеты), згідно якої інтеграл по замкненому контуру від функції комплексного аргументу з точністю до множника 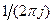дорівнює сумі вирахувань підінтегральної функції в особливих точках (полюсах 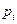), що охоплюються контуром інтегрування :

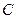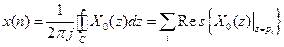. (7.57)

Обчислення вирахувань пов'язане з представленням функції 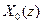у вигляді:

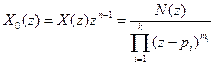, (7.58)

де 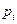є полюсом порядку .

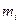Для знаходження вирахувань використовують наступні формули:

· У разі простого (одноразового) полюса, тобто полюсу з

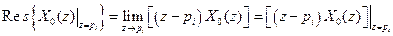(7.59)

· У разі кратного полюса, тобто полюсу го порядку,

. (7.60)

Приклад 1 . Визначити по зображенню 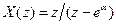відліки сигналу .

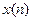Знайдемо підінтегральний вираз оберненого Z-перетворення:

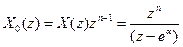Функція 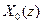має один простий полюс в точці . Відповідно до (7.59) отримуємо:

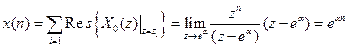Приклад 2. Знайти відліки сигналу 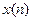по його Z -зображенню .

Підінтегральний вираз оберненого Z –перетворення дорівнює:

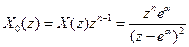Функція 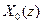має один двократний полюс . Відповідно до (7.60) отримуємо:

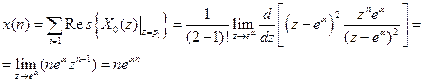Другим методом обчислення оберненого Z -перетворення, вживаним на практиці, є метод розкладання функції 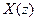на прості дроби. Функцію 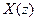представляють у вигляді суми елементарних дробів:

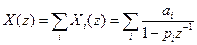де 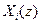- Z –перетворення з одним простим полюсом. З урахуванням того, що кожен доданок 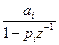має обернене Z–перетворення виду , отримуємо:

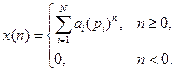
Приклад 3 . Обчислити обернене Z –перетворення функції .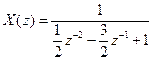

Представимо 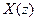у вигляді суми простих дробів :

Із зіставлення виду отриманих доданків з прикладами Z -перетворень типових дискретних сигналів (які були розглянуті) видно, що перший доданок відповідає одиничному стрибку з амплітудою, рівною 2, а другий - дискретній показовій функції 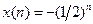. Отже, шукана послідовність має вигляд:

ЛІТЕРАТУРА

1. Цифровая обработка сигналов / А. Б. Сергиенко — СПб.: Питер, 2002. — 608 с: ил.. (Электронный ресурс)

2. Волощук Ю.Л. Сигнали та процеси в радіотехніці том. 1-4. - Харків: «СМІТ», 2003.

Дата добавления: 2022-01-22; просмотров: 28; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!