Второй замечательный предел, число е.
Число е определяется как следующий предел
, или 
, где число е = 2,718…., (3.13)
Число е является основанием так называемых натуральных логарифмов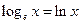 
.
Пример 1. Вычислить 
.
Решение. Числитель и знаменатель дроби при 
стремятся к нулю. Преобразуем функцию, выделим общий множитель
.
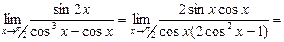
Пример 2. Вычислить 
.
Решение. Имеет место неопределенность вида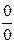 
. Преобразуем дробь, домножив числитель и знаменатель на выражение, сопряженное числителю
.
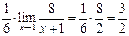Пример 3. Вычислить 
.
Решение. Имеет место неопределенность вида 
. Преобразуем функцию под знаком предела, домножив и поделив на сопряженное выражение.
.
Таким образом получили предел, в котором имеет место неопределенность вида 
. Наибольшая степень x первая, поэтому поделим числитель и знаменатель на x, получим
.
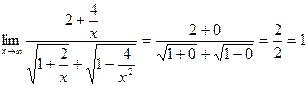Пример 4. Вычислить 
.
Решение. Так как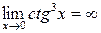 
, а 
, то имеет место неопределенность вида 
.
Выполним преобразования
.
Пример 5. Вычислить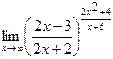 
.
Решение. Так как 
и 
, то имеет место неопределенность вида 
.
Возможны 2 способа решения примера.
1-й способ. Вспомним, что есть замечательный предел 
.
Используем этот замечательный предел, преобразовав исходный предел следующим образом:
.
Имеем
(здесь 
),
и
.
Таким образом,
.
2-й способ.
.
.
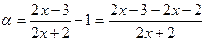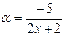Причем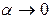 
при 
. Выразим 
из равенства
|
|
|
; 
; 
.
Таким образом,
.
Выполним замену
.
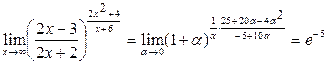Так как
, а 
,
то в итоге предел равен 
.
Глава 5. Непрерывность функции. Односторонние пределы.
Функция f(x) называется непрерывной в точке х0, если она определена в этой точке и некоторой ее окрестности, а также
(5.1)
Точки, в которых равенство (5.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка.
Обозначим за Dх разность между двумя значениями аргумента Dх = х2 –х1, а за Df (x) разность между двумя значениями функции Df(x) = f(x2) - f(x1). Тогда, если функция непрерывна, то бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если Dх® 0, то и Df (x) ® 0.
Введем понятие односторонних пределов. Число А называется пределом функции f(x) слева, если х®x0 оставаясь все время меньше х0 (x < x0). Запись предела слева
Аналогично вводится понятие предела справа, в этом случае х®x0 оставаясь все время больше х0 (x > x0). Запись предела справа
|
|
|
Для непрерывной функции предел слева совпадает с пределом справа и равен значению функции в точке х0
= 
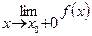= f(x0).
В точках разрыва цепочка равенств нарушается. Разрыв называется «разрывом первого рода», если все пределы конечны и «разрывом второго рода», если хотя бы один из пределов не существует или бесконечен.
Если хотя бы один из пределов равен бесконечности в точке х = х0 , то говорят, что в этой точке есть вертикальная асимптота. Функция, имеющая на конечном промежутке конечное число разрывов первого рода называется кусочно непрерывной.
Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.
Пример 1. Найти точки разрыва функции.
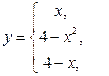если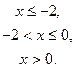 
Решение. На интервалах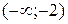 
, 
и 
функция непрерывна. Проверке подлежат только точк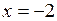и 
и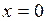 
.
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.
Рассмотрим точку .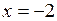
.
Вычислим односторонние пределы
, 
.
Так как односторонние пределы не совпадают, 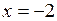- точка разрыва функции.
Рассмотрим точку .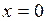
,
, 
,
- точка непрерывности функции, выполнены все условия непрерывности (рис. 5.1).
|
|
|
Рис. 5.1.
Пример 2. Исследовать поведение функции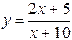 
вблизи точки разрыва. Построить схематический чертеж.
Решение. Область определения функции 
Точка разрыва 
. Найдем односторонние пределы
; 
.
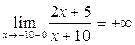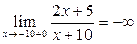Знак предела зависит от знаков числителя и знаменателя дроби. В обоих случаях числитель 
, но знаменатель в пределе слева остается отрицательным, приближаясь к нулю, а в пределе справа, приближаясь к нулю, знаменатель остается положительным. Схематичный чертеж представлен на рис. 5.2.
Рис. 5.2.
Дата добавления: 2022-01-22; просмотров: 17; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!