МЕТОДЫ НАХОЖДЕНИЯ ОЦЕНОК МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

ГЛАВА 7. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

 

ВВОДНЫЕ ЗАМЕЧАНИЯ

 

Из результатов предыдущей главы видно, что нахождение оценок максимального правдоподобия является существенным элементом адап­тивного байесова подхода и до некоторой степени даже его основой в случае параметрически заданной априорной неопределенности. Метод максимального правдоподобия, как мы видели ранее в гл. 2, 4, 5, имеет и большое самостоятельное значение. Он позволяет в ряде случаев най­ти минимаксное решение задачи с гарантированным уровнем риска и дает возможность выявить достаточные или квазидостаточные статисти­ки. В связи с этим в настоящей главе более подробно рассмотрим мето­ды получения и свойства оценок максимального правдоподобия.

Этому вопросу посвящена довольно обширная литература, начиная сранних работ по классической математической статистике, поэтому, возможно, значительная часть того, что будет изложено ниже, хорошо известна многим читателям. Это в особенности относится к случаю ре­гулярных оценок по совокупности независимых данных наблюде­ния, соответствующему этому случаю неравенству Крамера-Рао и асимптотической эффективности регулярных оценок максимального правдоподобия. Наряду с этим имеется много сравнительно малоиз­вестных аспектов метода максимального правдоподобия: влияние ста­тистической зависимости данных наблюдения на сходимость и точность оценок максимального правдоподобия; нерегулярность, когда функция правдоподобия недифференцируема по оцениваемым параметрам; ре­куррентные процедуры нахождения оценок максимального правдоподо­бия и их свойства и т. д. Наличие подобных аспектов, а также большое значение метода максимального правдоподобия для решения задач син­теза в условиях априорной неопределенности делают целесообразным систематическое изложение основных фактов, относящихся к методам получения и свойствам оценок максимального правдоподобия. Большин­ство этих фактов будет приведено без доказательства со ссылками на оригинальные и популярные работы, в которых такие доказательства имеются.

Прежде чем перейти к дальнейшему изложению, напомним некото­рые основные определения. Пусть имеется совокупность данных наблю­дения 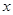, которую обычно будем представлять в виде вектора 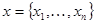, каждая компонента которого  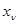соответствует одному наблюде­нию и, в свою очередь, может быть вектором того или иного порядка или даже отрезком реализации некоторого непрерывного случайного процесса. Пусть эти данные наблюдения зависят от некоторого парамет­ра  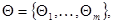размерности 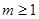. 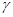(Нам удобно ввести здесь новое обозначение для неизвестных параметров, чтобы иметь возможность в дальнейшем понимать под  как параметры , характеризующие ап­риорную неопределенность в статистическом описани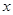и  и 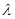, так и сами параметры 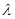, влияющие на последствия принимаемых решений и являющиеся предметом оценки в исходной задаче статистического ре­шения, так и, наконец, совокупность тех и других параметров.) Зависи­мость данных наблюдения  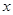от параметров  описывается функцией правдоподобия

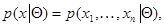                                    (7.1.1)

где 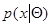 - плотность совместного распределения вероятности  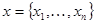при заданном значении , а оценка максимального прав­доподобия 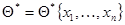 определяется из уравнения максимального правдоподобия

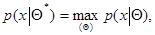                                  (7.1.2)

где максимум находится по области допустимых значений . Уравнение (7.1.2) эквивалентно следующему уравнению для логарифма функции правдоподобия, которым часто будем пользоваться в дальнейшем:

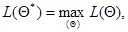                                         (7.1.3)

где

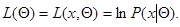                                  (7.1.4)

Если для каждого из допустимого множества значений для почти всех значений 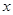 существуют частные производные  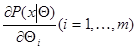причем

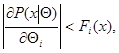
где 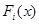 - интегрируемые по всему пространству  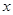функции, то оценка максимального правдоподобия является регулярной и уравнение макси­мального правдоподобия может быть представлено в одной из эквива­лентных форм

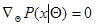                                                             (7.1.5)

или

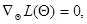                                                  (7.1.6)

где 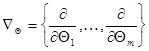 - оператор градиента по компонентам век­тора .

Регулярный случай, пожалуй, чаще всего встречается на практике. Однако во многих важных практических задачах свойство регулярности не выполняется, что заставляет рассматривать и более общий случай, для которого некоторые закономерности поведения регулярных оценок могут и не соблюдаться. Если наряду с оценкой максимального правдоподобия 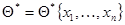 рассмотреть какую-либо другую функцию 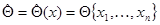, которая не является решением уравнения максимального прав­доподобия, то очевидно, что при весьма общих предположениях о виде этой функции можно считать ее оценкой параметра , более того, и совершенно произвольную функцию вектора 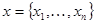 можно также назвать оценкой , хотя возможно, что точность этой оценки будет со­вершенно неудовлетворительной. В дальнейшем нам понадобится опре­деление регулярности и для оценки 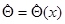 произвольного вида. Чтобы ввести это определение, зададим взаимно однозначное преобразование

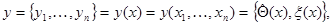                             (7.1.7)

где 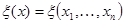 - некоторая многомерная функция  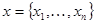дополняющая преобразование  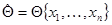до взаимно однозначного. В силу взаимной однозначности этого преобразования две совокупност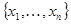и  и 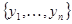 статистически эквивалентны, по­этому вместо исходной совокупности данных наблюдения  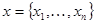можно рассматривать преобразованную совокупность 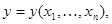статистическое описание которой задается функцией правдоподобия 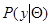, получающейся применением преобразования (7.1.7) к исходной функции правдоподобия (7.1.1).

Функцию правдоподобия 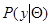, очевидно, можно записать в виде

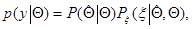                                   (7.1.8)

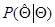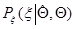где  и  - соответствующие условные плотности ве­роятности. Оценка  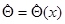называется регулярной, если для каждого  из заданного множества значений для почти всех значений  и 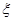 существуют частные производные 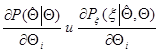, причем

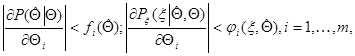
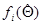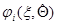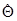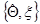где  и  - функции, интегрируемые по всему пространству  и  соответственно.

Совокупность этих условий несколько жестче, чем простое требова­ние дифференцируемости функции правдоподобия. Они накладывают определенные ограничения не только на 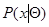, но и на возможные виды преобразования 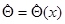, то есть на структуру оценочных функций.

Всякая оценка 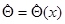 отличается от истинного значения . Про­стейшей характеристикой этого отличия является математическое ожи­дание разности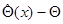

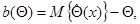                                                      (7.1.9)

вообще говоря, зависящее от  и называемое смещением оценки. Оцен­ка, для которой 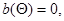 называется несмещенной.

Важным понятием является также понятие достаточной оценки. Оценка 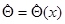 называется достаточной, если условная плотность ве­роятности  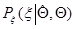в (7.1.8) не зависит от . Достаточная оценка является, очевидно, минимальной достаточной статистикой для пара­метра : достаточной в силу того, что она удовлетворяет основному требованию к любой достаточной статистике (гл. 2), а минимальной - в силу того, что размерность этой статистики (вектора 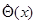) совпадает с размерностью вектора неизвестных параметров . Если существует какая-либо достаточная оценка 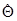, то любая лучшая оценка может быть только функцией .

 

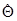МЕТОДЫ НАХОЖДЕНИЯ ОЦЕНОК МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

 

Уравнения максимального правдоподобия (7.1.2) или (7.1.3) опре­деляют общий способ нахождения оценок максимального правдоподо­бия как в регулярном, так и в нерегулярном случае. Существуют весьма разнообразные методы их решения, которые в достаточно общей форме можно классифицировать на два основных вида: конечные и рекуррент­ные. В первом случае оценка максимального правдоподобия получается сразу по всей совокупности имеющихся данных наблюдения х. Во вто­ром - решение уравнения максимального правдоподобия представляет собой процесс, в котором вычисление оценок производится многократно с постепенным увеличением совокупности данных наблюдения. В обоих случаях в зависимости от вида функции правдоподобия может быть по­лучено точное или приближенное решение. Рассмотрим возможные ме­тоды нахождения оценок максимального правдоподобия, обратив основ­ное внимание на рекуррентные процедуры.

 

Конечные методы

 

При решении уравнения правдоподобия (7.1.2), (7.1.3) может быть использован любой из известных методов максимизации функции век­торной переменной 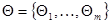. Только в редких случаях максими­зирующее значение - оценка максимального правдоподобия  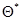нахо­дится точно. В частности, это заведомо удается сделать, если функция правдоподобия  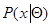такова, что

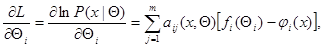                     (7.5.1)

где матрица 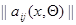 положительно (или отрицательно) определен­ная при всех  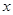и , а уравнения

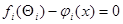                                           (7.5.2)

имеют решения. Эти решения

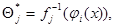                                           (7.5.3)

где 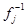 - функция, обратная 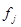, и являются компонентами вектора оцен­ки максимального правдоподобия.

Простейшим частным случаем (7.5.1) является случай, когда лога­рифм функции правдоподобия  квадратично зависит от , то есть

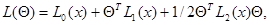                      (7.5.4)

где 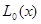- скаляр; 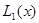- вектор той же размерности т, что и ;  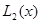- неособая матрица порядка 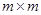. При этом оценка максималь­ного правдоподобия

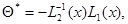                                             (7.5.5)

где 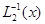- матрица, обратная .

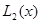Другим распространенным примером, для которого выполняется (7.5.1), является случай, когда

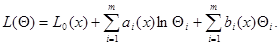                   (7.5.6)

В этом случае оценка максимального правдоподобия

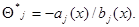                                           (7.5.7)

Число таких примеров, как соответствующих (7.5.1), так и несоот­ветствующих этому условию, но допускающих точное решение уравнения правдоподобия, в том числе и для нерегулярного случая (примеры § 7.4 и др.), довольно велико, однако еще более многочисленны случаи, когда точное аналитическое решение уравнения правдоподобия получить невозможно. При этом для нахождения оценки используются различ­ные приближенные методы. Выбор того или иного из них определяется исходя из точности приближенного решения и вычислительной просто­ты. В частности, в регулярном случае широко распространены различ­ные варианты итеративных процедур, в том числе градиентный метод, метод наискорейшего спуска, метод Ньютона, метод золотого сечения и т.д. Любой из них является методом последовательных приближений и при определенных условиях обеспечивает достаточно быструю схо­димость к истинному решению уравнения максимального правдоподо­бия. Приведем для примера алгоритм нахождения оценки максималь­ного правдоподобия, соответствующий методу Ньютона. В этом случае k -я итерация, определяющая очередное приближение 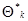 к оценке мак­симального правдоподобия 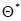, производится по правилу

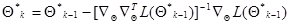,                       (7.5.8)

где 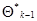 - приближение, полученное на 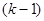-м шаге, а начальное приближение выбирается произвольно с учетом имеющихся представлений о существе задачи. Входящий в (7.5.8) оператор  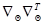представляет со­бой результат умножения вектора-столбца 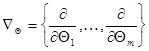на транс­понированный ему вектор (строку) и является матрицей вида  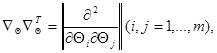так что результат воздействия этого опе­ратора на функцию  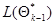также представляет собой матрицу

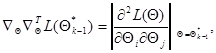                                   (7.5.9)

a 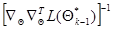, как всегда, обратная матрица.

Проиллюстрируем применение этого алгоритма на примере оценки единственного параметра 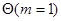 для случая, когда логарифм функ­ции правдоподобия  представляется в виде

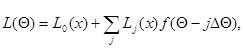                           (7.5.10)

где х - вектор некоторой размерности; 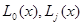- некоторые функ­ции х;  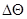- известная величина, функция  имеет единственный мак­симум (для определенности при 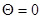) и является четной относительно этого значения, а суммирование производится по такому множеству значений j, что интервал от  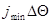до 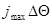 полностью перекрывает диапазон возможных значений параметра . К функции правдоподобия, соответствующей (7.5.10), приводят многие задачи радиотехнических измерений (частоты, задержки радиолокационного сигнала, направле­ния на источник излучения).

Выберем в качестве нулевого приближения 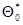 для оценки макси­мального правдоподобия  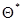величину, соответствующую какому-либо из дискретных значений 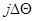, например 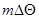. Для того чтобы это значение давало максимально возможную величину функции правдоподобия, очевидно, его нужно выбрать так, чтобы

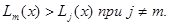                                            (7.5.11)

В силу свойств функции  выбор любого другого т приведет к уменьшению логарифма функции правдоподобия. Таким образом, наи­более правдоподобным дискретным приближением к оценке максималь­ного правдоподобия является величина

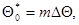                                                         (7.5.12)

где m определяется условием (7.5.11) и соответствует тому номеру j, для которого величина 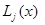 максимальна.

Следующее приближение вычисляется в соответствии с алгорит­мом Ньютона (7.5.8) и дается выражением

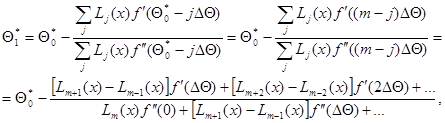   (7.5.13)

где учтена четность функции . Если последняя, как это бывает в практических задачах, достаточно быстро убывает с увеличением 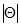, так что 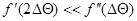и 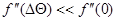, то в числителе и знаменате­ле выражения (7.5.13) можно ограничиться только первыми слагаемы­ми. В результате

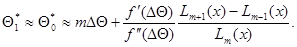                     (7.5.14)

то есть оценка получается зависящей только от наибольшей из величин 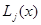 и двух ближайших к ней. Приближение (7.5.14), как правило, оказывается достаточно точным, и следующие итерации не требуются.

 

Рекуррентные методы

 

При большом объеме совокупности данных наблюдения х конечные методы решения уравнения правдоподобия приводят к значительным вычислительным трудностям, связанным с необходимостью запомина­ния большого числа исходных данных и промежуточных результатов вычислений. В связи с этим особый интерес представляют рекуррентные методы, в которых оценка максимального правдоподобия вычисляется по шагам с постепенно увеличивающейся точностью, причем каждый шаг связан с получением новых данных наблюдения, а рекуррентная проце­дура строится так, чтобы хранить в памяти по возможности наименьшее количество данных от предыдущих шагов. Дополнительным и весьма существенным с практической точки зрения преимуществом рекуррент­ных методов является готовность к выдаче результата на любом про­межуточном шаге.

Это обусловливает целесообразность применения рекуррентных ме­тодов даже в тех случаях, если удается получить точное решение урав­нения максимального правдоподобия конечным методом, и делает их еще более ценными, когда невозможно найти точное аналитическое вы­ражение для оценки максимального правдоподобия.

Пусть совокупность данных наблюдения представляет собой по­следовательность 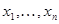 для описания которой введем вектор 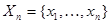. (Как всегда, каждая его компонента 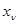, в свою очередь, может быть вектором, отрезком случайного процесса и т. д.). Пусть  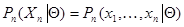- функция правдоподобия, а

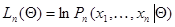                                    (7.5.15)

ее логарифм. Последний всегда можно представить в виде

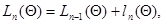                                    (7.5.16)

где

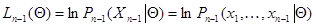                      (7.5.17)

- логарифм функции правдоподобия для совокупности данных наблю­дения 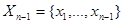 без последнего значения, а

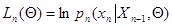                                      (7.5.18)

- логарифм условной плотности вероятности значения 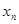 при заданных значениях  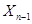и .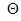

Представление (7,5.16) для логарифма функции правдоподобия яв­ляется основой для получения рекуррентной процедуры вычисления оценки максимального правдоподобия. Рассмотрим регулярный случай. При этом оценка максимального правдоподобия может быть найдена как решение уравнения

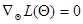,                                                  (7.5.19)

которое отличается от (7.1.6) только введением индекса п у логарифма функции правдоподобия.

Обозначим решение этого уравнения через 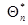 подчеркнув тем са­мым, что эта оценка получена по совокупности данных наблюдения 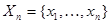. Аналогично обозначим через  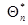решение уравнения  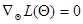- оценку максимального правдоподобия, полученную по совокупности данных .

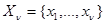Уравнение (7.5.19) можно переписать с учетом (7.5.16) в следующем виде:

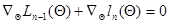.                                                  (7.5.20)

Разложим левую часть (7.5.20) в ряд Тейлора в окрестности точки 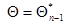. При этом

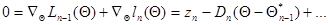                               (7.5.21)

где

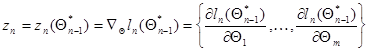           (7.5.22)

- вектор градиента функции 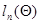   в точке 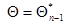; слагаемое  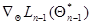обращается в нуль благодаря тому,  что 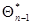, является решением уравнения правдоподобия для предыдущего (п - 1)-го шага:

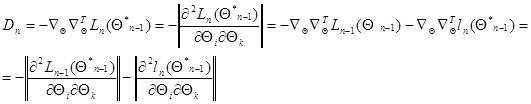(7.5.23)

- симметричная матрица вторых производных логарифма функции правдоподобия в точке 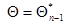, взятая с обратным знаком, аненапи­санные члены разложения имеют квадратичный и более высокий поря­док малости относительно разности 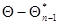. Пренебрегая этими по­следними, получаем следующее приближенное решение уравнения ма­ксимального правдоподобия:

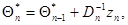                                              (7.5.24)

где 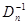- матрица, обратная .

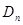Это решение представлено в форме рекуррентного соотношения, определяющего очередное значение оценки 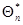 через оценку  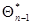на предыдущем шаге и поправку 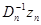, зависящую от имеющихся данных наблюдения непосредственно и через предыдущую оценку. Поправка формируется как произведение градиента логарифма условной плотно­сти вероятности  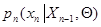вновь полученного значения х_n в точке 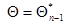, равной предыдущей оценке, на весовую матрицу 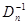. По­следняя определяется выражением (7.5.23) и также зависит от оценки  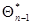на предыдущем шаге, а ее зависимость от новых данных наблюдения целиком определяется видом логарифма условной плотности веро­ятности .

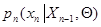По форме соотношение (7.5.24) очень похоже на (7.5.8), реализую­щее итеративный способ вычисления оценки максимального правдоподо­бия по методу Ньютона. Однако на самом деле они существенно отли­чаются друг от друга. В (7.5.8) поправка к предыдущему значению оцен­ки определяется величиной градиента логарифма всей функции правдо­подобия, который всегда зависит от всех имеющихся данных наблюде­ния 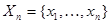, что требует запоминания всей этой совокупности. В соответствии с (7.5.24) поправка к  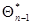определяется величиной гра­диента 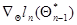, который благодаря свойствам условной плотности вероятности  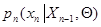фактически зависит только от тех значений  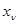( 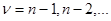), которые находятся в сильной статистической связи с х_n. Это различие является следствием специального выбора предыдущего приближения  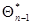как оценки максимального правдоподобия, найденной по уменьшенной на одно значение совокупности данных наблюдения 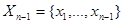, и особенно ярко проявляется при независимых значениях  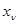( 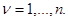). В этом последнем случае

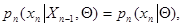
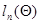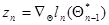благодаря чему  зависит только от  и х_n, а градиент  - только от предыдущего значения оценки  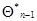и вновь полученных на п-мшаге данных наблюдения 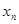. Поэтому при незави­симых значениях  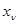для формирования вектора  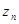не требуется запо­минать с предыдущего шага никакой иной информации, кроме значения оценки .

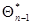Аналогично, в случае марковской последовательности данных на­блюдения, то есть при

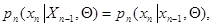
вектор 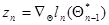 зависит только от 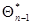, текущего  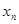и одного предыдущего значения 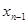.В этом случае для вычисления  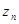требуется запомнить с предыдущего шага, помимо значения 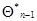, еще только значение 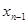, но не всю совокупность данных наблюдения, как в ите­ративной процедуре. В общем случае для вычисления  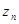может потребоваться запоминание большего числа предыдущих значений  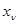( 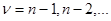), однако из-за необходимости учета только тех значе­ний 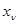, которые статистически зависимы с 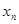, это число практически всегда меньше полного объема совокупности данных наблюдения 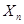. Так, если вектор 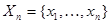описывает временную последователь­ность, то количество подлежащих запоминанию членов этой последова­тельности определяется временем ее корреляции, а относительная их доля убывает обратно пропорционально n, как и в случае независимых значений .

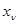Рассмотрим теперь структуру весовой матрицы 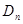, входящей в ре­куррентное соотношение (7.5.24). Согласно определению (7.5.23), из-за наличия слагаемого  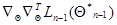она, вообще говоря, зависит от всех значений  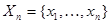даже при независимых значениях 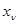, что ли­шает рекуррентное соотношение (7.5.24) преимуществ, связанных с воз­можным сокращением количества запоминаемых с предыдущего шага данных. Существует несколько способов приближенного вычисления ма­трицы 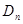, которые устраняют этот недостаток.

Первый из них основан на более последовательном использовании основного предположения о малом различии двух очередных значений оценк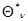и  и 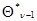, которое является основой для получения рекур­рентного соотношения (7.5.24). Это позволяет получить аналогичное ре­куррентное соотношение для весовой матрицы 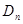.Действительно, используя малость  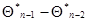из (7.5.23), имеем

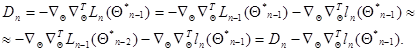        (7.5.25)

Введя обозначение

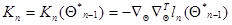,                                          (7.5.26)

из (7.5.24) и (7.5.25) получим систему рекуррентных соотношений для вектора 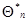 и весовой матрицы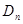

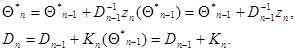               (7.5.27)

Эта система совместно с начальными значениями  и 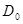 полностью определяет значение оценки  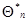на любом шаге, требуя на каждом из них вычисления только градиента  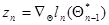и матрицы вторых производных  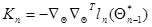от логарифма условной плотности вероятности для текущего наблюдаемого значения 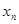. Начальные значе­ния выбираются с учетом имеющихся априорных данных о возможных значениях и диапазоне изменения параметров , а при полном отсутст­вии этих данных принимаются нулевыми ( , ).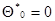

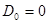При независимых значениях 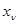 система рекуррентных соотношений (7.5.27), очевидно, описывает многомерный (размерности 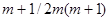) марковский случайный процесс, компонента которого  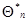сходит­ся к истинному значению параметра , а компонента 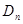 сходится к ин­формационной матрице Фишера  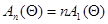(7.3.8), где  - истинное значение оцениваемого параметра, и неограниченно увеличивается с ростом п. Аналогичные свойства сходимости система (7.5.27) имеет и при более общихусловиях, если последовательность 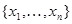 явля­ется эргодической.

Второй из упомянутых способов основан на замене матрицы вторых производных от логарифма функции правдоподобия 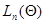 ее матема­тическим ожиданием - информационной матрицей Фишера, которая с учетом (7.5.16) может быть записана в виде:

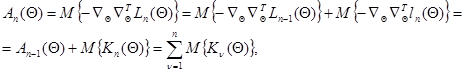    (7.5.28)

где аналогично (7.5.26)

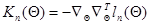.                                       (7.5.29)

Заменяя в (7.5.24) матрицу 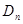 матрицей 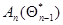, получаем ре­куррентное соотношение

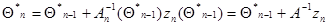                               (7.5.30)

для приближенного вычисления оценок максимального правдоподобия, предложенное Сакрисоном (в оригинале для независимых одина­ково распределенных 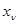, когда  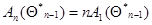и 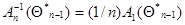. Это рекуррентное соотношение проще системы (7.5.27), поскольку оптимальная весовая матрица  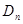заменена ее мате­матическим ожиданием, и для ее нахождения не требуются имеющиеся данные наблюдения, кроме тех, которые сконцентрированы в значении оценки 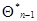. В то же время очевидно, что подобная замена означает необходимость выполнения дополнительного по сравнению с (7.5.27) требования близости матрицы вторых производных к своему математи­ческому ожиданию.

Если плотность распределения вероятности 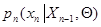 и матри­ца  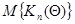меняются от шага к шагу, прямое нахождение  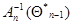на каждом шаге может потребовать слишком большого числа вычисле­ний. При этом за счет дополнительного уменьшения точности ре­зультатов, определяемого неравенством нулю малых разностей 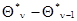, можно перейти к рекуррентному вычислению приближен­ного значения матрицы 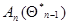. Возвращаясь к прежнему обозначе­нию  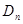для этого приближенного значения, получаем еще одну систему рекуррентных соотношений

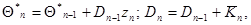                          (7.5.31)

где

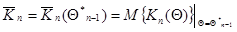                              (7.5.32)

- математическое ожидание матрицы 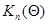 (информационная матри­ца Фишера для одного наблюдения 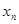), взятое в точке 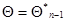. Эта система отличается от (7.5.27) тем, что во втором из рекуррентных соот­ношений (7.5.31) не участвуют непосредственно данные наблюдения .

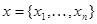Любая из рассмотренных выше систем рекуррентных соотношений является совершенно точной, если функция 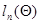 квадратично зависит от , и дополнительно матрица вторых производных 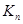 не зависит от 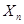. Фактически это соответствует случаю независимых нормально рас­пределенных (не обязательно одинаково) значений  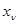с неизвестным математическим ожиданием , которое и представляет собой оценивае­мый параметр.

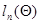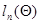Система рекуррентных соотношений (7.5.24) дает точное решение уравнения максимального правдоподобия в гораздо более широких условиях при единственном требовании, чтобы функция  квадра­тично зависела от . При этом зависимость  от 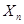 произвольна, что соответствует широкому классу распределений вероятности совокуп­ности  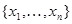как с независимыми, так и с зависимыми значениями.

Наряду с рассмотренными общими способами существует еще ряд методов выбора матрицы весовых коэффициентов 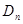 в рекуррентном соотношении (7.5.24), приспособленных к тем или иным конкретным ограничениям. Простейшим из них является выбор  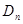в виде диагональной матрицы, так что 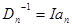, (I - единичная матрица), где  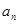- убывающая последовательность чис­ловых коэффициентов, выбираемая независимо от свойств функции правдоподобия так же, как в процедуре стохастической аппроксимации Робинса - Монро, которая будет рассмотрена в следующих главах.

Стоит отметить, что любые итерационные или рекуррентные про­цедуры нахождения оценок максимального правдоподобия в общем случае являются приближенными. Поэтому, вообще говоря, для оценок, получающихся в результате применения этих процедур, состоятельность, асимптотическую эффективность и асимптотическую нормальность нуж­но доказывать заново. Для итеративных процедур необходимые свой­ства оценок гарантируются тем, что в принципе такие процедуры при соответствующем числе итераций дают решение уравнения правдоподо­бия с любой наперед заданной точностью. Для рекуррентных процедур типа (7.5.27), (7.5.30), (7.5.31) и других имеются специальные доказа­тельства. При этом, помимо требования регулярности, предъявляются некоторые дополнительные требования:

- на поведение функции 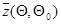 (7.2.2) при различных значениях | 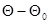|, для достижения с помощью рекуррентной процедуры глобаль­ного максимума этой функции в точке 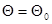, соответствующей истинно­му значению параметра;

- на порядок роста вторых моментов производных логарифма функции правдоподобия при больших по модулю значениях . Эти тре­бования являются следствием более общих усло­вий сходимости в точку всех или части компонент марковского случай­ного процесса, к которому приводит та или иная рекуррентная про­цедура.

       В заключение отметим также, что в том случае, когда существует точное решение уравнения максимального правдоподобия, оно практиче­ски всегда может быть представлено в рекуррентном виде. Приведем два простых разнородных примера. Так, элементарная оценка неизвест­ного математического ожидания  нормальной случайной величины по совокупности n ее выборочных значений 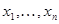 в виде арифме­тического среднего 

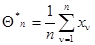                                                      (7.5.33)

является оценкой максимального правдоподобия и может быть пред­ставлена в рекуррентном виде:

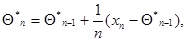                                                   (7.5.34)

что является самым простым частным случаем (7.5.30) при

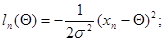
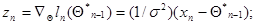                             (7.5.35)

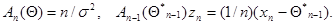
Другой пример - это нерегулярная оценка максимального правдо­подобия для параметра  - ширины прямоугольного распределения – из (7.4.2), которая также может быть определена рекуррентным соот­ношением

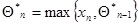                                                     (7.5.36)

с начальным условием 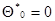. Это рекуррентное соотношение уже дру­гого типа: его правую часть нельзя представить в виде суммы предыду­щей оценки и малой поправки, что является следствием нерегулярности этого примера; однако оно обладает всеми преимуществами рекуррент­ного подхода: требует запоминания с предыдущего шага всего одного числа - оценки  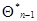- и резко сокращает перебор до одного сравнения  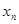с 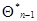 вместо сравнения всех значений .

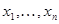Приведенные примеры иллюстрируют преимущества рекуррентных методов даже в том случае, когда уравнение максимального правдопо­добия допускает точное решение, ибо простота аналитического пред­ставления результата не тождественна вычислительной простоте его по­лучения.

7.5.3. Переход к непрерывному времени. Дифференциальные уравнения для оценок максимального правдоподобия

 

Рассмотрим теперь специальный случай, когда имеющиеся данные наблюдения х описываются не совокупностью выборочных точек 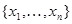, а представляют собой отрезок реализации некоторого процесса 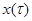, зависящего от параметров , заданный на интервале 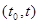, при­чем длина этого интервала может увеличиваться при наблюдении (мо­мент времени t является переменным).

Для статистического описания данных наблюдения в этом случае вводится функционал отношения правдоподобия, представляющий собой предел при 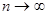, max 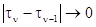 отношения плотности распределе­ния вероятности совокупности значений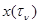 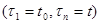 при произ­вольно заданном значении  к аналогичной плотности вероятности при некотором фиксированном значении 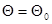, а в некоторых случаях, когда  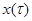допускает представлени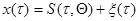е , где 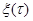 - случай­ный процесс, не зависящий от , к плотности вероятности совокупности значений 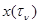 при условии, что 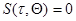. Использование функционала отношения правдоподобия позволяет исключить формальные труд­ности определения плотности вероятности, возникающие при переходе к непрерывному времени.

Логарифм функционала отношения правдоподобия может быть представлен в виде

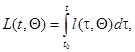                                            (7.5.37)

где 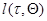 - некоторый функционал процесса  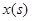на интервале 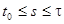. В некоторых случаях функционал  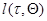вырождается в функ­цию, зависящую только от значения 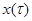. Так, если

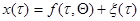.                                           (7.5.38)

где 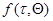 - известная функция времени  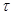и параметров , а 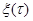 - дельта-коррелированный случайный процесс («белый» шум) со спек­тральной плотностью N_o,то, выбирая в качестве знаменателя отношения правдоподобия распределения вероятности х при 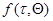, будем иметь

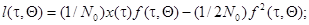                  (7.5.39)

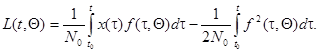.                    (7.5.40)

Пусть 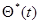 - оценка максимального правдоподобия параметра , построенная по реализации процесса 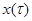 на интервале 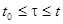,то есть решение уравнения максимального правдоподобия

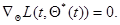                                               (7.5.41)

Дифференцируя левую часть этого уравнения по времени, получаем

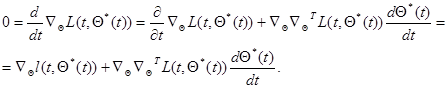(7.5.42)

Вводя обозначения

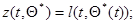                                                        (7.5.43)

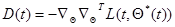                                  (7.5.44)

и решая уравнение (7.5.42) относительно 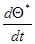, получаем диффе­ренциальное уравнение для оценки максимального правдоподобия

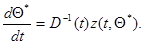                                        (7.5.45)

Матрица 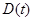, в свою очередь, согласно (7.5.37) определяется диффе­ренциальным уравнением

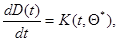                                           (7.5.46)

где

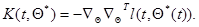                                (7.5.47)

Так же, как в дискретном случае, матрица 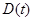 в (7.5.45), (7.5.47) мо­жет быть заменена своим математическим ожиданием — информационной матрицей Фишера  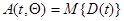при значении 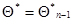, а диф­ференциальное уравнение (7.5.46) для весовой матрицы  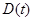- урав­нением

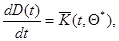                                                (7.5.48)

где аналогично дискретному случаю

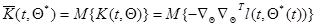                      (7.5.49)

- математическое ожидание матрицы вторых производных .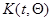

Совокупность дифференциальных уравнений (7.5.45), (7.5.46) или (7.5.45), (7.5.48) совместно с начальными условиями, относительно вы­бора которых остается в силе все сказанное для дискретного случая, полностью определяет оценку максимального правдоподобия 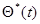 для любого момента времени. Эта совокупность может быть смоделирована с помощью соответствующих, вообще говоря, нелинейных аналоговых устройств или при подходящей дискретизации по времени решена с по­мощью ЭВМ. Отметим в заключение одну из модификаций этих урав­нений, позволяющую избежать необходимости обращения матрицы .

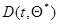Вводя обозначение

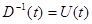                                                      (7.5.50)

и дифференцируя по времени соотношение 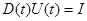, где I - единич­ная матрица, получаем с помощью (7.5.46) дифференциальное уравне­ние, определяющее непосредственно матрицу :

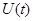и дифференцируя по времени соотношение 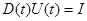, где I - единич­ная матрица, получаем с помощью (7.5.46) дифференциальное уравне­ние, определяющее непосредственно матрицу :

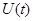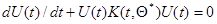                                   (7.5.51)

(и аналогично при замене 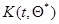  на 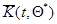), которое совместно с уравнением (7.5.45)

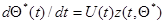
определяет оценку 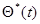, не требуя обращения матриц. При этом имеет место переход от простейшего линейного дифференциального уравнения (7.5.46) к нелинейному относительно  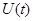дифференциальному уравне­нию (7.5.51) типа Риккати.

---

Дата добавления: 2022-01-22; просмотров: 54; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!