Изучить данный материал, сделать конспект, решить неравенства.
Урок 53-54: Логарифмические неравенства
Мы уже говорили о логарифмической функции и ее свойствах. Важным свойством, которым мы пользовались для решения логарифмических уравнений: монотонность.
Для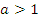 
график логарифмической функции выглядит следующим образом:
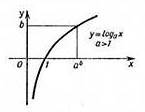
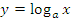- возрастающая функция: чем больше 
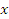, тем больше 
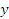. Значит, 
.
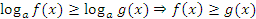В отличие от уравнений, при решении логарифмических неравенствпроверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ: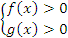 
Объединяя, получаем: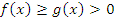 
.
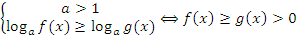
Для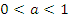 
график логарифмической функции выглядит следующим образом:
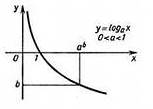
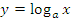- убывающая функция: чем больше 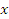, тем меньше 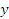. Значит, 
.
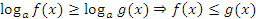ОДЗ: .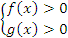
Объединяя, получаем: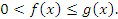 
.
При решении логарифмических неравенств лучше всего начинать с проверки ОДЗ
Рассмотрим такой полезный факт: как быстро определить знак логарифма?
Рассмотрим два случая:
1) : 
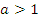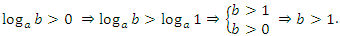
2) : 
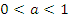Таким образом,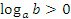 
, если 
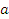и 
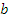лежат по одну сторону от 1, и 
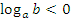, есл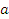и и 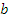лежат по разные стороны от 1.
Основные виды логарифмических неравенств
1) Простейшие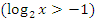 
2) Сводящиеся к простейшим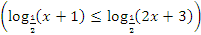 
3) С использованием свойств логарифмов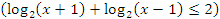 
4) С заменой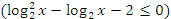 
5) С переменной в основании 
Рассмотрим решение логарифмического неравенства, когда основание логарифма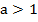 
.
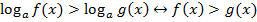,то есть знак неравенства сохраняется.
ОДЗ представлено системой:
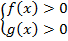
Решением исходного неравенства является эквивалентное неравенство 
, поэтому для соблюдения ОДЗ достаточно проверить меньшее из чисел получаем систему неравенств, которая соответствует исходному неравенству:
|
|
|
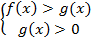
Решение более сложных логарифмических неравенств
Пример 1:
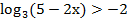
Согласно методике решения простейших логарифмичеких неравенств, первым действием необходимо уравнять основания логарифмов, в данном случае представить правую часть в виде логарифма с требуемым основанием:
Получаем неравенство:
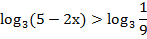
Учтем ОДЗ: 5-2х>0
х>2,5
Поскольку основание логарифма больше единицы, в эквивалентной системе знак неравенства сохранится:
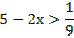
Преобразуем:
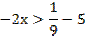
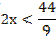
Ответ: х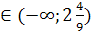 
Пример 2:
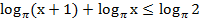
Учтем ОДЗ:
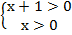
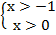
ОДЗ: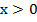 
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
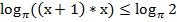
Нам известно, что число Пи больше единицы (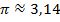 
). Поэтому в эквивалентном неравенстве знак исходного неравенства сохраняется:
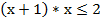
Преобразуем полученное неравенство:
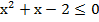
Корни квадратного уравнения, стоящего в левой части, согласно теореме Виета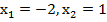 
. Имеем параболу, ветви которой направлены вверх. Интересующие нас значения находятся между корней уравнения:
Ответ с учетом ОДЗ: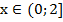 
Сведение к простейшему логарифмическому неравенству часто осуществляется с помощью замены переменных.
|
|
|
Пример 3:
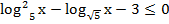
Приведем второй член к основанию 5:
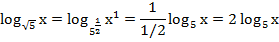
Получили неравенство:
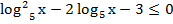
замена: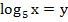 
Имеем:
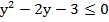
Согласно теореме Виета корни квадратного уравнения, стоящего в левой части: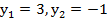 
. Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями.
Вернемся к исходным переменным:
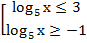
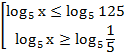
Преобразуем согласно определению логарифма:
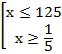
Ответ: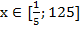 
Пример 4:
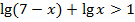
Учтем ОДЗ:
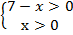
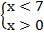
ОДЗ: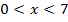 
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
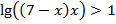
Преобразуем правую часть в логарифм с требуемым основанием:
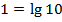
Имеем неравенство:
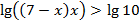
Основание логарифма больше единицы, получаем эквивалентное неравенство с тем же знаком:
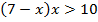
Преобразуем:
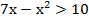
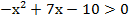
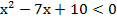
Согласно теореме Виета корни квадратного уравнения, стоящего в левой части: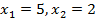 
. Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями:
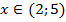
Ответ с учетом ОДЗ: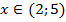
Системы логарифмических неравенств решаются аналогично системам показательных неравенств: каждое из неравенств решается по отдельности, а затем находится пересечение.
Пример: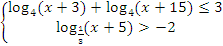 
|
|
|
Закрепление материала
а)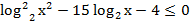 
;
б)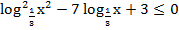 
;
в)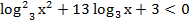 
;
г)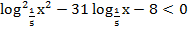 
;
Изучить данный материал, сделать конспект, решить неравенства.
Фотоотчет выслать либо личным сообщением в вК на страничку Инга Агеенко либо на электронную почту distInga @ rambler . ru
Дата добавления: 2022-01-22; просмотров: 66; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!