Наибольшее и наименьшее значение

Функция называется возрастающей на множестве из обл. определения, если для любых х1 и х2, таких, что х1 < x2 - выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.
Функция называется убывающей на множестве из обл. определения , если для любых х1 и х2, таких, что х1 < x2 - выполняется неравенство f(x1)>f(x2). То есть большему значению аргумента, соответствует меньшее значение функции.

Понятия "возрастание" и "убывание" функции очень легко понять, если внимательно посмотреть на графики функции. Для возрастающей функции: мы как бы поднимаемся в горку, для убывающей соответственно - спускаемся. Общий вид возрастающих и убывающих функции представлен на графиках ниже.

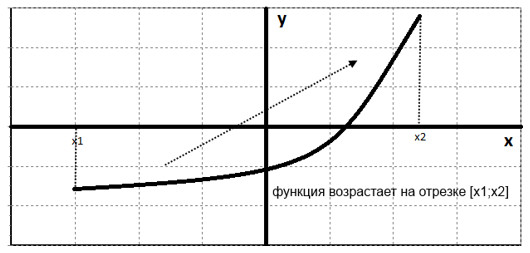
Возрастание и убывание функции в общем случае называется монотонностью. То есть, наша задача -это найти промежутки убывания и возрастания функции. В общем случае это формулируется так: найти промежутки монотонности или исследовать функцию на монотонность.

Пример

Исследовать на монотонность функцию y=3x+2.
Решение: Проверим функцию для любых х1 и х2 и пусть х1 < x2.
f(x1)=3x1+2
f(x2)=3x2+2
Поскольку, х1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.

Ограниченность функции

Функцию y=f(x)

называют ограниченной снизу на множестве Х ⊂ D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.

Функцию y=f(x)

называют ограниченной сверху на множестве Х ⊂ D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.

Если промежуток Х не указывается, то считают, что функция ограничена на всей области определения. Функция ограниченная и сверху, и снизу называется ограниченной.

Ограниченность функции легко читается по графику. Можно провести некоторую прямую
у=а

, и если функция выше этой прямой, то ограниченность снизу. Если ниже, то соответственно сверху. Ниже представлен график ограниченной снизу функции. График ограниченной функции, ребята, попробуйте нарисовать сами.

Пример

Исследовать на ограниченность функцию y=√16−x2.
Решение: Корень квадратный из некоторого числа больше либо равен нуля. Очевидно, что наша функция, также больше либо равна нуля, то есть ограниченна снизу.
Корень квадратный мы можем извлекать только из неотрицательного числа, тогда 16−x2≥0.
Решением нашего неравенства будет промежуток [-4;4]. На этом отрезке 16−x2≤16 или √16−x2≤4, но это значит ограниченность сверху.
Ответ: наша функция ограниченна двумя прямыми у=0 и у=4.

Наибольшее и наименьшее значение

Наименьшим значение функции y= f(x) на множестве Х ⊂ D(f), называется некоторое число m, такое, что:
a) Существует некоторое х0, что f(x0)=m
б) Для любого хϵХ, выполняется f(x)≥f(x0)

Наибольшим значение функции y=f(x) на множестве Х ⊂ D(f), называется некоторое число m, такое что:
a) Существует некоторое х0, что f(x0)=m
б) Для любого хϵХ, выполняется f(x)≤f(x0)

Наибольшее и наименьшее значение принято обозначать y_наиб. и y_наим..

Понятия ограниченности и наибольшего с наименьшим значением функции тесно связаны. Выполняются следующие утверждения:
а) Если существует наименьшее значение у функции, то она ограничена снизу.
б) Если существует наибольшее значение у функции, то она ограничена сверху.
в) Если функция не ограничена сверху, то наибольшего значения не существует.
г) Если функция не ограничена снизу, то наименьшего значения не существует.

Если требуются найти свойства функции, то последовательность поиска свойств такова:
а) Область определения.
б) Монотонность.
в) Ограниченность.
г) Наибольшее и наименьшее значение.
д) Непрерывность.
е) Область значений.

Пример

Найти свойства функции y=−2x+5.
Решение.
а) Область определения D(y)=(-∞;+∞).
б) Монотонность. Проверим для любых значений х1 и х2 и пусть х1 < x2.
f(x1)=−2x1+2.
f(x2)=−2x2+2.
Поскольку х1 < x2, то f(x1) < f(x2), то есть большему значению аргумента, соответствует меньшее значение функции. Функция убывает.
в) Ограниченность. Очевидно, что функция не ограничена.
г) Наибольшее и наименьшее значение. Поскольку функция не ограничена, то наибольшего и наименьшего значений не существует.
д) Непрерывность. График нашей функции не имеет разрывов, тогда функция непрерывна.
е) Область значений. Е(у)=(-∞;+∞).

Домашнее задание.1.Конспект прочитать. Правила выучить.

2.Построить график функции. Найти свойства функции:
а) y=2x+7,
б) y=4x.

Мы поможем в написании ваших работ!