Решеточные модели в теории перколяции, понятие и характеристики порога перколяции (протекания).
Раздел 2. Основы теории перколяции
Общие определения
Т еория перколяции(протекания или просачивания) - современный статистический метод компьютерного моделирования и анализа процессов связывания случайным образом (стохастически) первичных материальных объектов (атомов, молекул, электрических или магнитных моментов, дисперсных частиц, зародышей новой фазы, флуктуаций плотности и концентрации и т.п.) в кластеры (связные структуры или агрегаты, связанные домены, сквозные поры и т.п.) с прохождением критической точки – порога перколяции, т.е. образования непрерывного кластера, пронизывающего всю систему и имеющего фрактальную структуру.
В материаловедении и технологиях материалов теория перколяции в сочетании с методами фрактальная геометрия и наиболее эффективно применяется для описания критических явлений, структуры и свойств образующихся фрактальных кластеров в процессах:
· агрегирования твердых частиц в коллоидных растворах, дисперсиях и аэрозолях с золь/гель переходом от конечных кластеров частиц (золя) к непрерывному кластеру – гелю («физическое» гелеобразование);
· трехмерных реакций образования сетчатых полимеров с переходом от конечных молекул (золя) к непрерывной полимерной сетке - гелю («химическое» гелеобразование);
· формирования пористой структуры твердых тел с переходом от пор конечных размеров к непрерывной (сквозной) пористости;
|
|
|
· агрегирования адсорбируемых молекул или осаждающихся частиц на твердых поверхностях с формированием двух или трех-мерных островковых структур конечных размеров и переходом к бесконечной (непрерывной) структуре;
· агрегирования частиц новой фазы на начальных стадиях фазовых превращений по механизму зарождения новой фазы (в переходах 1-го рода) и перерождения фаз (в непрерывных переходах 2-го рода) с формированием гетерогенных структур – матричных и статистических дисперсий с взаимопроникающими фазами;
· формирования и агрегирования жидкоподобных доменов в критической точке системы «жидкость-пар» с возникновением сверхкритического состояния жидкости;
· формирования и агрегирования твердоподобных доменов вблизи критической точки сильно переохлажденных жидкостей, которые служат скрытой причиной стеклования некристаллизующихся жидкостей и способствуют образованию сверхкритических зародышей в кристаллизующихся жидкостях;
· непрерывного перерождения аморфного состояния бинарных растворов вблизи критической температуры термодинамической совместимости компонентов в результате стабильного роста и взаимодействия флуктуаций концентрации на начальной стадии спинодального распада;
|
|
|
· возникновения и взаимодействия диссипативных структур при потере устойчивости термодинамически неравновесных систем в необратимых процессах переноса при больших градиентах и потоках вдали от равновесия;
· агрегирования электрических или магнитных моментов в домены с увеличением параметра порядка и достижением критических точек (точек Кюри) при фазовых переходах 2-го рода в сегнето- (ферро)электриках и ферромагнетиках соответственно;
· агрегирования куперовских электронных пар с достижением критической точки перехода проводника в сверхпроводящее состояние.
Эта теория описывает характеристики массы или размеров и распределения по размерам кластеров, образующихся из первичных элементов, взаимодействующих между собой случайным образом в неупорядоченных средах в зависимости от глубины прохождения (степени превращения) процесса агрегирования и определяет условия прохождения порога перколяции как критического геометрического (топологического) перехода от конечных кластеров к непрерывному бесконечному, а также для оценки изменения структуры и свойств образующихся кластеров вблизи порога перколяции. Впервые эта теория разрабатывалась применительно к определению условий возникновения непрерывной (сквозной) пористости в твердом теле с проявлением протекания жидкости и получила свое название от латинского слова perc ō l ā re, обозначающего «протекание» или «просачивание».
|
|
|
Теория перколяции включает чисто статистический подход, положения (теоремы и постулаты) которого описывают наиболее вероятные (равновесные) предельные параметры кластеров при большом числе взаимодействующих первичных элементов, а также кинетический подход, описывающий механизм и кинетику начальной эволюции (роста и агрегирования) кластеров и базирующийся на использовании кинетического уравнения кластерообразования (уравнения Смолуховского). Соответственно, данный раздел лекционного курса состоит из двух подразделов, посвященных этим подходам.
2.2 Современные с татистические подходы и модели в теории перколяции
Решеточные модели в теории перколяции, понятие и характеристики порога перколяции (протекания).
В основе современных статистических моделей в теории перколяции лежит теория вероятности на графах или решетках. Эти модели разрабатываются с использованием специальных компьютерных алгоритмов и программ и получением конкретных численных параметров, характеризующих кластеры в моделируемой системе. До этих подходов основой статистической теории кластерообразования служила классическая аналитическая теория, разработанная Флори и Штокмайером для трехмерных реакций образования сетчатых полимеров. Эта теория базируется на определении вероятности и критической степени ветвления молекул при реакции z -функциональных мономеров, например, Si(OH)4 c z =4 в золь-гель технологии, с аналитическим выводом общих соотношений для предельных параметров непрерывной полимерной сетки (геля) - глубины превращения мономеров, структуры и содержания геля и не присоединенных к нему разветвленных молекул (золя). Основными ограничениями в анализе такого процесса являются не изменяющаяся в ходе процесса реакционная способность (вероятность взаимодействия p) функциональных групп, отсутствие в структуре замкнутых петель (циклов) и статистическая гомогенность (однофазность) реакционной среды. При этом вероятность ветвления молекул без образования замкнутых петель в простейшем случае мономера с реакционно-способными группами, взаимодействующими между собой, как в случае Si(OH)4, равна W = ( z -1) p ≥1 (3.1а), а критическая степень превращения, необходимая для формирования геля, рс=1/( z -1) (3.1б).
|
|
|
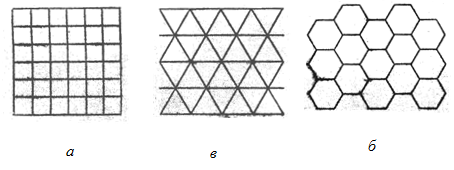
Как уже указывалось, современная статистическая теория перколяции относится к теории вероятности на графах, к которым в геометрии относят множества точек (вершин) и набор соединяющих их линий (ребер) с заданным координационным числом z, т.е. числом ребер, сходящихся в одном узле. Часто их называют решетками или сетями с узлами (вершинами), соединенными связями (ребрами). В статистической теории перколяции наиболее часто используются регулярные графы - дискретные (состоящие из замкнутых ячеек заданного типа) и открытые (ветвящиеся незамкнутые) решётки в d -мерном эвклидовом пространстве, примеры которых для плоскости (d=2) показаны на рис. 1.
| 
г
|
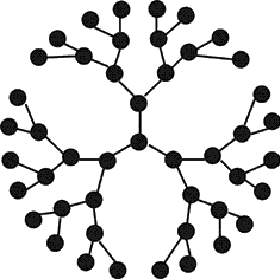
Рис.1. Примеры регулярных плоских решеток с различными координационными числами z: (а-в) дискретных - квадратной (z=4); треугольной(z=6); шестиугольной(z=3) соответственно и (г) открытой или ветвящейся решетки Бете или дерева Кейли (z=3).
Классическая аналитическая теория гелеобразования или кластерообразования (теория Флори-Штокмайера) соответствует теории вероятности на решетке Бете или дереве Кейли (рис. 1г ), собенностью которых является ветвление без образования замкнутых циклов.
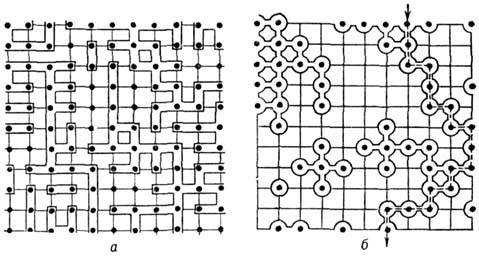
В современной статистической теории перколяции, ставшей классической, обычно используется моделирование на простых дискретных решетках в двумерном и (реже) трехмерном пространстве с использованием различных алгоритмов и программ. На рис. 2 показаны примеры решения так называемых задач узлов (мест) и связей в статистической теории перколяции на квадратной двумерной решетке.
в
Рис. 2. Схемы решения задачи связей (а) и узлов или мест (б) при заданной степени превращения (доли образованных связей и заполненных узлов) р, а также задач узлов при различном р с прохождением порога протекания или перколяции (в) на плоских квадратных решетках.
В задаче узлов (перколяция по узлам) в дискретной решетке случайным образом (см. рис.2б) заполняют (закрашивают) пересечения линий (узлы). При заполнении двух соседних узлов они образуют кластер. С возрастанием степени превращеия (доли или вероятности заполненных узлов) р формируются кластеры размером (числом узлов) s со средним значением s ср в количестве (наборе или распределении по размерам) ns . Критическое значением доли заполненных узлов (рс), при котором возникает непрерывный кластер, пронизывающий всю решетку, т.е. s ср →∞, определяет порог перколяции.
В другом варианте численного моделирования на решетках, называемом задачей связей (см. рис.2в), удаляют случайным образом линии (связи) между узлами. Порог перколяции при решении задачи связей меньше, чем при решении задачи узлов, так как связь соединяет только два узла, тогда как узел связывается несколькими связями в зависимости от координационного числа решетки z ( в случае квадратной решетки z=4).
Точность оценки рс в обоихвариантах численного моделирования на решетках зависит от размеров решетки L , определяющей общее число узлов и связей в ней. При конечных размерах решеток вероятность перехода порога пеколяции охватывает широкую область степеней превращения, а при L →∞ рс является критической точкой (Рис. 3). Поэтому точное значение рс как критической степени превращения при моделировании на решетках определяется при размере решетки L →∞.
Рис. 3. Схематическое изображение вероятности прохождения порога перколяции Р в зависимости от степени превращения р при различных размерах решеток: плавная линия соответствует L<∞, ступенчатая L→∞.
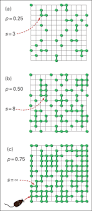
На рис. 4 приведен пример перколяционного кластера, полученного при реальном компьютерном моделировании задачи узлов на квадратной решетке и зависимость вероятности его возникновения от степени превращеия при таком моделировании.
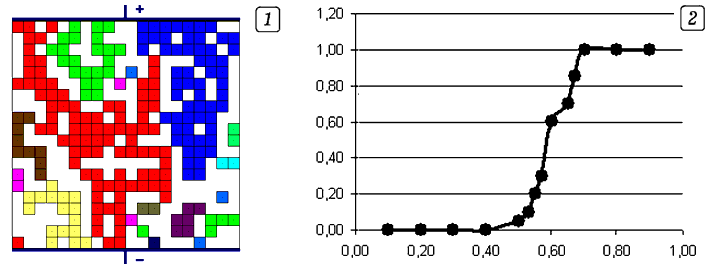
Рис. 4. Изображение перколяционного кластера на квадратной решетке (ячейки перколяционного кластера окрашены красным, другими цветами окрашены узлы более мелких кластеров) (1) и зависимость вероятности вероятности прохождения порога перколяции Р от доли заполненных узлов решетки р при конечном ее размере (2).
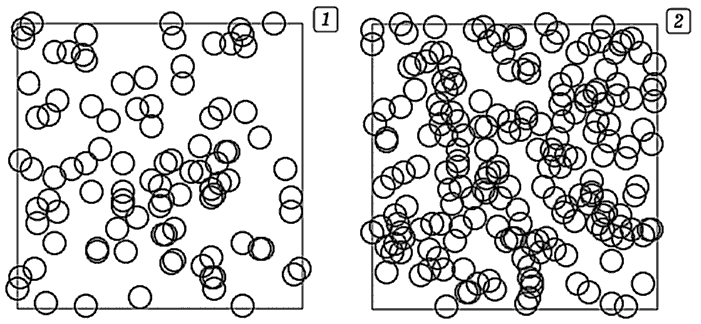
Помимо дискретных решетчатых моделей в статистических теориях перколяции при компьютерном моделировании используются также непрерывные модели, в которых в пустое пространство случайным образом вводятся первичные элементы заданной формы, контактирование которых или их перекрывание соответствует образованию кластеров. На рис. 5 показаны примеры таких моделей при отсутствии (а) и наличии (б,в) перколяционного кластера.
сс 
(а) (б) (в)
Рис. 5. Примеры непрерывных моделей образования кластеров на плоскости введением заданного количества кружков до (а) и после формирования перколяционного кластера (б,в).
Таким образом, основным постулатом и явлением статистической теории перколяции, подтвержденным большим объемом численного моделирования на различных решетках, служит представление о возникновении при некоторой критической степени превращения связей или узлов (р=рс) одного и только одного непрерывного (простирающегося по всей решетке, бесконечного, стягивающего, пронизывающего всю систему), или перколяционного кластера. Хотя при повторных численных экспериментах каждый раз получаются различные конфигурации кластеров,рс при заданном типе и размерности решетки стремится к постоянному значению при размере решетки L →∞ . Критический переход от конечных кластеров, размер которых меньше размера решетки, к возникновению одного непрерывного кластера, размер которого равен размеру решетки (соединяет края решетки,), называется геометрическим перколяционным переходом.
Определенные статистически (аналитически и в результате компьютерного моделирования на решетках) пороги перколяции для типичных 2-х и 3-х мерных решеток обобщены в таблице 1.
Таблица 1.
Характеристики основных типов 2-х и 3-х мерных дискретных решеток и пороги перколяции, установленные при решении задач связей и узлов (мест) на этих решетках
|
Размерность пространства, d |
Тип решетки |
Координационное число решетки, z | Порог перколяции |
Произведение zрсс | |||
| Классич. теория гелеобразования, рс=1/z-1 | Статистическая задача связей, рсс | Статистическая задача узлов, рсу | |||||
|
2 | Треугольная | 6 | 0,200 | 0,347*) | 0,500*) | 2,1 | |
| Квадратная | 4 | 0,333 | 0,500*) | 0.593 | 2,0 | ||
| Шестигранная (пчелиые соты) | 3 | 0,5 | 0,653*) | 0,698 | 2,0 | ||
|
3
| Кубическая | 6 | 0,200 | 0,247 | 0,311 | 1,50 | |
| Гранецентрированная кубическая (гекасагональная) | 12 | 0,091 | 0,119 | 0,198 | 1,43 | ||
| Тетраэдрическая (алмазная) | 4 | 0,333 | 0, 388 | 0,428 | 1,56 | ||
| Нерегулярная (статистическая) | ~8 | ~0,143 | - | ~0,27 | - | ||
| 6 | Простая кубическая | 12 | 0,091 | 0,094 | 0,081 | 1,13 | |
Примечание: Звездочкой *) помечены данные, полученные аналитически, все остальные – компьютерным моделированием.
Из приведенных данных видно, и это подтверждается экспериментально, что статистические теории дают значения порога перколяции, существенно большие, чем классическая теория теория гелеобразования Флори-Штокмайера, в которой не учитывается образование замкнутых петель, уменьшающих верояность ветвления и, соответственно, прохождения порога перколяции. Данные для гипотетических решеток более высокой размерности пространства, чем 3, в которых образование замкнутых петель также значительно менее вероятно, показывают, что хорошее согласие между классической теорией, соответствующей перколяции на решетке Бете, и перколяцией на простых решетках, наблюдается, начиная с размерности пространства, равной 6 (см. нижний ряд табл 1). При этом моделирование задач узлов на всех решетках дает более высокие значения порога перколяции по сравнению с задачами связей, так как каждая связь связывает только два узла, а каждый узел связывается числом связей, равным координационному числу решетки.
Данные, приведенные впоследнем столбце таблицы 1 показыают, что призведение степени превращения связей в пороге перколяции на координационное число решетки определяется только ее размерностью и практически не зависит от типа решетки.
Важнейшей характеристикой перколяционного кластера является его мощность Р∞, соответствующая вероятности образования простирающегося по всей решетке кластера и равная доле первичных элементов (узлов или связей в решеточных моделях), входящих в него, т.е. вероятности того, что случайно выбранный первичный элемент принадлежит этому кластеру. До порога перколяциимощность перколяционногокластераР∞(р<рс) =0, а после этого перехода доля принадлежащих перколяционному кластеру узлов или связей больше нуля, и на предельной стадии кластерообразования Р∞(р>рс)→1 (рис.6). При этом доля узлов или связей, принадлежащих конечным кластерам, соответственно, стремится к нулю.
Рис. 6. Схематическое изображение зависимостей Р∞ от степени превращения р.
Следовательно, по определению Р∞(р) =0 при р≤рс, и при р=рс перколяционный процесс претерпевает переход от состояния локальной связности к состоянию, в котором связность распространяется неограниченно далеко. При этом установлено, что зависимость Р∞(р) описывается степенной (скейлинговой) функцией: Р ∞ (р)~(р-рс) β(3.1), где показатель степени β является универсальой константой (критическим индексом), величина которого не зависит от типа решетки, а определяется только размерностью эвклидова пространства: для плоских решеток β = 5/36=0,1389... и для 3-х мерных β ≈ 0,4.
(Примечание: знак ~ используется здесь и далее для обозначения асимптотической пропорциональности, что избавляет от необходимости указания коэффициента пропорциональности)
Примером практического примения скейлинговой функци (3.1) является описание изменения намагничивания и поляризации парамагнетиков и параэлектриков соответственно при фазовом переходе 2-го рода – в точке Кюри. При охлаждении от температуры выше точки Кюри локальный порядок магнитных моментов и электрических диполей в результате самопроизвольного упорядочивания (ориентации собразованием доменов и их агрегирования, или кластеризации) возрастает в определенных пределах. В точке Кюри (Тс) возникает непрерывный кластер доменов, и намагниченность парамагнетика М(Т) и поляризация параэлектрика П(Т) резко нарастают по скейлинговому закону – пропорционально (Тс-Т) β при β, лежащем в интервале 0,3-0,4 при трехмерном переходе.
Основными размерными характерстиками кластеров служат их средний размер, или масса s ср (р) как число входящих первичных элементов и корреляционная длина или протяженность (длина) связностиξ как квадратный корень из среднего квадрата расстояния между занятыми узлами, принадлежащими одному и тому же кластеру, так называемого средне-квадратичного радиуса инерции или гирации (гирорадиуса). Средне-квадратичный радиус инерции определяется как средний квадрат расстояния всех элементов кластера от его центра массы (инерции), и для кластера, содержащего sузлов, определяется соотношением:
(3.2а)
Длина связности, или корреляционная длина кластера рассчитывается по Rg 2 ( s ), усредненному по распределению размеров кластеров ns (р):
(3.2б),
где распределение размеров кластеров ns (р) рассматривается как функция степени превращения р и равно среднему числу кластеров размером s ср (р) в расчете на один узел.
До порога перколяции sср(р) соответствует средней массе (числу узлов), а ξ(р) – средней протяженности конечных кластеров, а после порога перколяции – соответственно, массе и протяженности характерных элементов непрерывного кластера. Например, при «химическом» гелеобразовании до точки гелеобразования sср(р) соответствует средней молекулярной массе разветвленных макромолекул, а ξ(р) – их средней протяженности (расстоянию между концами или диаметру клубка), которые резко возрастают с увеличением степени превращения и приближении к точке гелеобразования. После точки гелеобразования (возникновения непрерывной полимерной сетки) sср(р) соответствует средней молекулярной массе цепей между узлами сетки, а ξ(р) – их среднему расстоянию между узлами сетки, которые резко уменьшаются при дальнейшем возрастании степени превращения. При гелеобразовании коллоидных дисперсий до порога перколяции sср(р) и ξ(р) также характеризуют массу и протяженность докритичских кластеров частиц, а после порога перколяции – элементы структуры непрерывного кластера.
Вблизи порога протекания обе размерные характеристики кластеров, sср(р) и ξ(р), как и Р ∞(р) (см. соотношение (3.1) , являются резко выраженными степенными (скейлинговыми) функциями: sср(р)~(р-рс)- γ (3.2а) ;ξ(р)~(р-рс)- ν (3.2б), которыевыводятся масштабным преобразованием гомогенных функций. Показатели степени этих функций (критические индексы γ и ν) являются универсальными константами и не зависят от типа решетки, а определяются только размерностью пространства, причем они одинаковы по обе стороны порога протекания. Критические индексы рассчитывается методом перенормировки (ренормогруппы).
В точке перколяционного перехода функции sср (р) и ξ(р) претерпевают дивергенцию: при р=рс они стремятся к бесконечно большому значению (сингулярны), а при р>рс онистремятся к нулю (Рис.7).
Рис. 7 Схематическое изображение зависимостей s ср (р) или ξ (р)
На рис.8 приведены зависимости среднего размера кластеров и их корреляционной длины до порога перколяции, а также мощности перколяционного кластера и связанной с ним относительной электропроводности после порога перколяции от степени превращения, полученные при моделировании задачи электропроводящих связей на квадратной решетке.
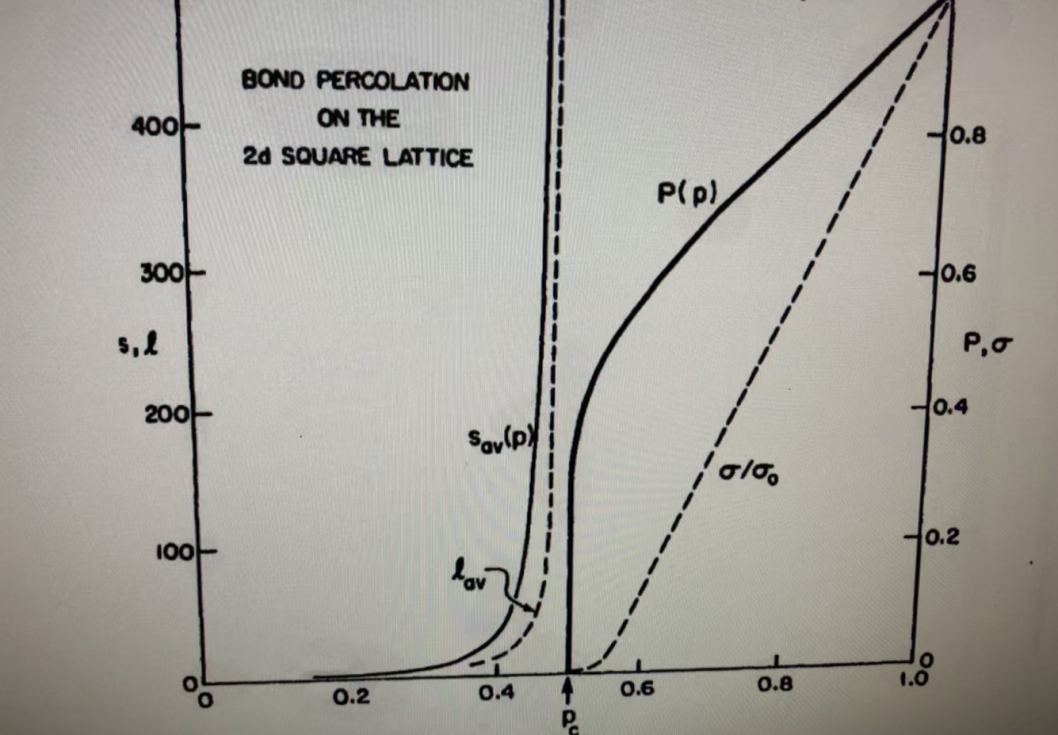
Рис.8. Полученные при компьютерном моделировании на двухмерной квадратной решетке электропроводящих связей зависимости среднего размера (массы) кластеров sav ( p ) и их корреляционной длины lav ( p ), а также мощности перколяционного кластера Р(р) иотносительной электропроводности σ/σ0 от степени превращения.
Распределение кластеров по массе и корреляционной длине, также как и зависимости размерных характеристик кластеров от степени превращения (см. соотношения (3.2а,б) , описываются степенными (скейлинговыми) функциями с универсальными показателями степени:ns (s)~s-τ (3.2в) и ξ(s)~s ς (3.2г). Значения всех критических индексов вблизи порога перколяции для различных размерностей решеток обобщены в таблице 2.
Таблица 2.
Значения основных критических индексов вблизи порога перколяции для различных размерностей решеток.
|
Характеристика кластеров |
Универсальный индекс | Значения индекса при различной размерности решетки, d | ||
| d=2 | d=3 | d=6 (соответствует классической теории) | ||
| Мощность непрерывного кластера, Р(р)~(р-рс)β | β | 5/36= 0,14 | 0,40-0,42 | 1 |
| Средняя масса кластеров, sср(р)~(р-рс)-γ | γ | 43/18= 2,4 | 1,7-1,8 | 1 |
| Корреляционная длина кластеров, ξ(р) ~(р-рс)- ν | ν | 4/3= 1,35 | 0,850-0,875 | 0,5 |
| Распределение по массе, ns (s) ~ s-τ при s→∞ | τ | 2,06 | 2,2 | 5/2= 2,5 |
| Распределение по корреляционной длине, ξ(s) ~ s ς при s→∞ | ς | 0,525 1,9 | 0,40 2,5 | 0,25 4 |
Первые три универсальных индекса (β, γ и ν) в теории перкляции связваны между собой через размерность пространства d соотношением, называемым гиперскейлингом: d ν=2β+γ (3.3).
Особенностью критических индексов, определяемых в статистической теории перколяции при малых (реальных) размерностях пространства d, является их сравнительно малые отличия между собой и существенно большие их отличии от критических индексов, определенных для больших размерностей пространства и, соответственно, по классической теории.
Универсальность рассмотренных выше скейлинговых функций обусловлена самоподобием или масштабной инвариантностью перколяционных кластеров, являющихся фрактальными, что подробнее излагается ниже.
2.2.2 Фрактальность, мультифрактальность и самоподобие статистических геометрических кластеров вблизи порога перколяции
В большом количестве численных экспериментов при решении статистических задач теории перколяции на решетках установлено, что размеры образующихся наибольших кластеров smax, характеризуемые их массой, т.е. количеством узлов или связей в них, различным образом зависят от размера решетки L при различных степенях превращения. При р<рсмасса наибольшего кластера, не являющегося перколяционным, пропорциональна логарифму размера решетки: smax ( L )~ lnL (3.4 a ). При р>рс она пропорциональна L в степени d ( smax ( L )~ Ld (3.4б), где показатель степени d – целочисленная размерность решетки. Вблизи порога перколяции (при р≈рс) показатель степени в этой функции является дробным и соответствует фрактальной размерности наибольшего кластера: smax ( L )~ LDF (3.4в). Это служит доказательством того, что перколяционные кластеры, как непрерывные кластеры вблизи порога перколяци, являются фрактальными.
Для оценки фрактальной размерности и доказательства самоподобия таких кластеров наиболее эффективно использовано моделирование на узлах 2-х мерной треугольной или квадратной решетки при L →∞, которое позволяет производить численные эксперименты с очень малой погрешностью. На плоской треугольной решетке такое моделирование в задаче узлов дает точные значения порога перколяции (рс=1/2) и фрактальной размерности перколяцинного кластера (DF =91/48=1,895...), а при использовании плоской квадратной решетки рс=0,593 и DF =1,89±0,01. Обратите внимание на близкие значения фрактальной размерности перколяционного кластера при обоих типах решеток одной размерности.
На рис. 9 приведены вид перколяционного кластера на треугольной решетке при р=рс=1/2 (а) и зависимость числа узлов в нем от линейного размера решетки (б), дающая точное значение фрактальной размерности кластера.
(а) (б)
Рис.9. Перколяционный кластер на треугольной решетке при р=рс (а) и число узлов в непрерывном кластере при рс=1/2 ( S ∞ ) в треугольной решетке в зависимости от линейного размера L решетки в двойных логарифмических координатах с наклоном прямой (угловым коэффициентом), соответствующем точному значению фрактальной размерности DF =91/48=1,895…
Адекватной моделью перколяционного кластера, получаемого на треугольной двухмерной решетке при решение задачи узлов, может служить регулярная фрактальная кривая, построенная Мандельбротом и Гивеном (Рис.10) – она является самоподобной и дает практически аналогичные решеточной модели значения фрактальной размерности DF = 1,892....
Рис.10. Схема построения кривой Мандельброта-Гивена из дробления на три образующего элемента, состоящего из восьми отрезков - четырех, замкнутых в квадрат (петлю), и четырех свободных (ветвей), т.е. в образующем элементе на каждой стадии дробления 8 прямолинейных отрезков заменяются отрезками (копиями), уменьшенными в 3 раза: N =8, r=1/3 и
DF = ln 8/ ln 3=1,892.
Для доказательства того, что перколяционный кластер является статистически самоподобным, было проведено преобразование подобия на треугольной решетке 180х180 с заданным коэффициентом подобия (b =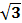 
) (Рис.11).
Рис.11. Результат преобразования подобия перколяционного кластер на треугольной решетке 180х180 с коэффициентом подобия b =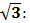 
исходный кластер (а), его преобразование с коэффициентом подобия b = 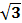(в) и вставка преобразованного кластера в то место исходного кластера, которое обведено рамкой (г).
Следует напомнить, что преобразование подобия заключается в том, что при умножении независимой переменной однородной функции, какой является функция smax ( L )~ LDF (3.4в), на любое число b (коэффициент подобия) соблюдается соотношение: smax ( bL )= bDF smax ( L ) или smax ( L )= bDF smax ( L / b ) (3.4г),т.е. масса перколяционного кластера при двух масштабах связана скейлинговым соотношением, показатель степени (критический индекс) которого соответствует его фрактальной размерности.
Численными экспериментами установлено, что масса фрактального перколяционного кластера или число узлов в нем вблизи порога перколяции связаны с его среднеквадратичным радиусом инерции (гирорадиусом) ( Rg ), значительно меньшим размера решетки (Rg<<L), степенной функцией: s ∞ ( Rg )~ RgDF (3.5а). При этом мощность перколяционного кластера (доля связей или узлов в нем) вблизи порога перколяции как функция корреляционной длины (Р(ξ)) также описывается степенной функцией: Р(ξ)~ξ D F - d(3.5б), где d - размерность пространства.
При учете того, что непрерывный перколяционный кластер содержит не связанные с ним конечные кластеры, средний размер (число узлов) и средний радиус инерции (гирорадиус) кластеров как функции размера решетки (s ср ( L ) и Rg 2 ( s )ср ( L ) соответственно), их средний размер как функция корреляционной длины (s ср (ξ)), а также распределение количества кластеров (ns (s) и их корреляционной длины ξ(s)) по размерам (массе) вблизи порога протекания также определяются степенными (скейлинговыми) соотношениями, показатели степени в которых связаны с фрактальной размерностьюDF: s ср ( L )~ L (2 D F - d ) (3.6а);Rg 2 ( s )ср ( L )~ L 2-( d - D F ) (3.6б), s ср (ξ)~ξ2 D F - d(3.6в), ns (s)~ s -( d + D F )/ D F (3.6г) и ξ(s)~s 1/ D F (3.6д) соответственно, где d - размерность пространства.
Соотношения (3.6а) и (3.6б) показывают, что с увеличением размера решетки вблизи порога перколяции средние размеры кластеров увеличиваются менее резко, чем перколяционного кластера (см. smax ~ LDF (3.4в). Важное значение имеют связи критических индексов ns (s) и ξ(s) в соотношениях 3.2в,г (ns (s)~s-τ и ξ(s)~s ς )) с фрактальной размерностью кластеров (τ= ( d + DF )/ DF и ς=1/ DF). Эти связи являются характеристиками кластеров с точки зрения оценки степени изменения их массы (количества связей или узлов в них) при возрастании их размера в зависимости от степени заполнения пространства (фрактальной размерности).
Все приведенные в этом подразделе степенные функции и критические показатели в них, выраженные через фрактальную размерность перколяционного кластера и пространственную (эвклидову) размерность решетки, обусловлены применимостью идей скейлинга к перколяционному кластеру как самоподобной структуре и, соответственно, к критическому поведению при фазовых переходах второго рода. Они также широко используются при численном моделировании для определения критических показателей вблизи порога перколяции.
Во многих реальных задачах, решаемых в теории перколяции (течение жидкости в пористых системах и электрпроводность в гетерогенных смесях проводящих и диэлектрических фаз) протекание жидкости или тока возможно только по основной части (остову) перколяционного кластера и не может осуществляться по некоторым обособленным частям (ветвям), которые связаны с остовом через едиственный узел или связь. Остов включает все узлы или связи, лежащие на всех возможных траекториях не самопересекающегося случайного блуждания, которое не может привести в обособленную ветвь, потому что иначе для возвращения в остов пришлось бы дважды побывать в том единственном узле или связи, которые связывают обособленную ветвь. Конкретный пример остова перколяционного кластера, полученного при моделировании по узлам квадратной решетки, показан на рис. 12. Остов связывает узел, находящийся в центре решетки, с узлами на ее границе. Перколяционный кластер при пороге перколяции рс=0,593 содержит 6261 узел, а его остов всего 3341 узел.
Рис.12. Перколяционный кластер и его остов, показанный черным цветом и полученный по результатам моделирования на квадратной решетке размером 147х147
При этом перколяционный кластер в целом имеет фрактальную размерность DF =1,89, а фрактальная размерность остова D В =1,61, т.е. D В ≤ DF. Зависимость массы остова перколяционного кластера от размера решетки описывается аналогично кластеру в целом скейлинговым сосотношением с показателем степени – фрактальной размерностью остова: МВ( L )~ L D В(3.7). Аналогичные результаты получены и в других модельных экспериментах.
Адекватной моделью остова перколяционного кластера, описываемого в целом кривой Мандельброта-Гивена (см. рис.10), является упрощенная кривая Мандельброта-Гивена, получаемая с помощью образующего элемента с петлей их четырех отрезков и двух боковых ветвей (рис.13).
Рис.13. Схема построения упрощенной кривой Мандельброта-Гивена, моделирующей остов кластера, образуемого первичной кривой Мандельброта-Гивена, привденноц на рис.10.
Фрактальная размерность такой кривой без свободных («висячих») концов DB=ln6/ln3=1,63..., так как в образующем элементе на каждой стадии преобразования шесть прямолинейных участков (N=6) заменяются отрезками (копиями), уменьшенными в 3 раза (r=1/3).
Если вообразить кривую Мандельброта-Гивена, изображенную на рис.10, изготовленной из электропроводящего материала, в которой ток течет от от левого конца к правому, то очевидно, что ни в одной ветви, образуемых из вертикальных отрезков образующего элемента тока не будет. Ток может течь только по кривой, которая получится, если осечь все ветви, соединенные с исходными прямолинейным участком только одной связью, т.е. по остову, изображенному на рис. 13 в виде упрощенной кривой Мандельброта-Гивена.
На рис.14 схематически изображен токонесущий остов и мертвые концы в бесконечном кластере вблизи порога протекания в виде двумерной сетки с размером ячеек, равным корреляционной длине с заданным сопротивлением между двумя узлами.
Рис.14. Схема токонесушей структуры (остова) перколяционного кластера в виде двумерной сетки с подвешенными «мертвыми» частями.
На рис.15 приведены зависимость электропроводности гидрогеля от концентрации проводящих частиц (а) и вид токопроводящего остова перколяционного кластера, образованного такими частицами (б).
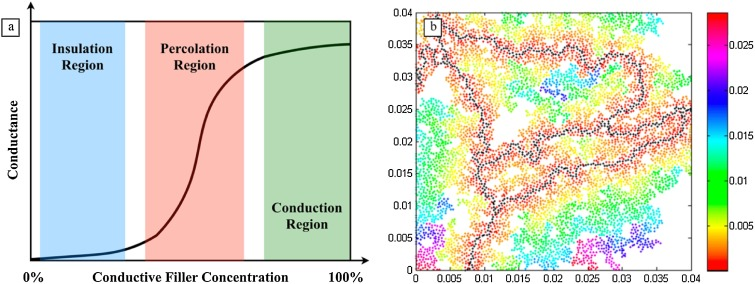
(а) (б)
Рис.15. Зависимость электропроводности диэлектрика от концентрации проводящих частиц (а) (Conductance – Проводимость; Conductive Filler Concentration - концентрация проводящего наполнителя; Insulation Region - область отсутствия проводимости, Percolation Region - область перколяционногоперехода; Conduction Region - область проводимости) и вид токопроводящего остова перколяционного кластера, образованного такими частицами (б).
====30.09.21
Дата добавления: 2021-12-10; просмотров: 538; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!