Свойства и графики некоторых функций

Тема: свойства функций

    С двумя свойствами функций вы уже знакомы – это область определения и область значений функций. Рассмотрим следующие свойства функции – точка пересечения графика функции с осями координат.

    Так как ось Оу (ось ординат) характерна тем, что любая точка на ней имеет координату х = 0, а для оси Ох (ось абсцисс) – любая точка на ней имеет координату у = 0, то точки пересечения графика с осями координат ищутся очень просто.

    Точка пересечения с осью Оу равна значению функции у(х) при х = 0, т.е. у(0).

    Точка пересечения с осью Ох являются корнями уравнений у(х) = 0 и называются нулями функции.

    Пример 1

    Рассмотрим функцию у(х) = – х² + 6х – 8.

    Найдем точки пересечения графика этой функции с осями координат. Чтобы определить точку пересечения графика с осью ординат, вычислим значение функции у(х) при х = 0

у(0) = – 0² + 6 · 0 – 8 = – 8. Получим координаты этой точки (0; – 8).

    Теперь определим точки пересечения графика данной функции с осью абсцисс. Для это в функцию у = – х² + 6х – 8 подставим значение у = 0 и получим квадратное уравнение 0 = – х² + 6х – 8 или – х² + 6х – 8 = 0. Решим его:

– х² + 6х – 8 = 0 | · (– 1)

х² – 6х + 8 = 0 

а = 1; b = – 6; с = 8

D = b² – 4ac

D = (– 6)² – 4 · 1 · 8

D = 36 – 32

D = 4, D > 0

                             

                                 

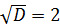
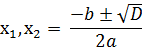
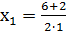
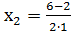
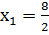
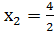
х₁ = 4                                  х₂ = 2

    Поэтому график данной функции пересекается с осью абсцисс в двух точках с координатами (4; 0) и (2; 0). Для наглядности на рисунке приведен график данной функции.

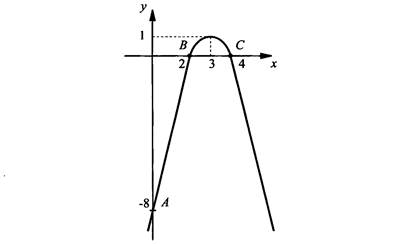
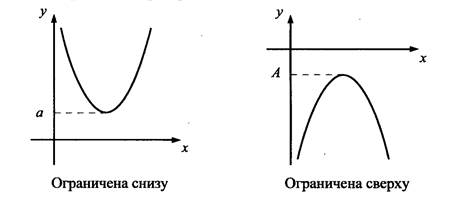
           Следующее свойство – ограниченность функции. Функция называется ограниченной снизу, если все значения функции не меньше некоторого числа а. (т.е. у(х) ≥ а).

    Функция называется ограниченной сверху, если все значения функции не больше некоторого числа а (т.е. у(х) ≤ а).   

    Если функция ограничена снизу и сверху, то она называется ограниченной.

    На рисунке приведены графики ограниченных и неограниченных функций.

    Пример 2

    Докажем, что функция у(х) = – х² + 6х – 8 ограничена сверху.

    Выделим в функции у(х) = – (х² + 6х – 8) полный квадрат разности. Для этого в скобках прибавим и вычтем единицу. Получаем:

у(х) = – (х² + 6х – 8) = – ((х² – 6х + 9) – 1) = – ((х – 3)² – 1) = 1 – (х – 3)².

    Так как при всех значения х величина (х – 3)² ≥ 0, величина – (х – 3)² ≤ 0 то 1 – (х – 3)² ≤ 1, т.е. у(х) ≤ 1. Тогда по определения данная функция ограничена сверху (при этом число а, входящее в определение, равно 1). Из графика примера 1 наглядно видно, что при всех значения х значения у(х) ≤ 1.  

    Рассмотрим еще одно свойство функции – монотонность (т.н. возрастание и убывание функции).

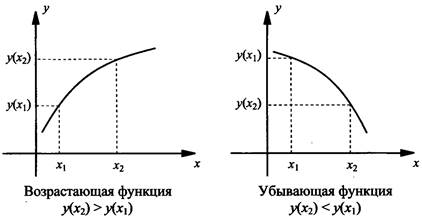
    Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции (т.е. если х₂ > х₁, то у(х₂) > у(х₁)).

    Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т.е. если х₂ > х₁, то у(х₂) < у(х₁)).

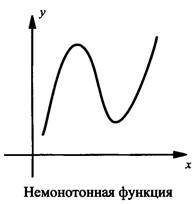
    На рисунке приведены графики монотонных (возрастающей и убывающей) и немонотонной функции. 

           Пример 3

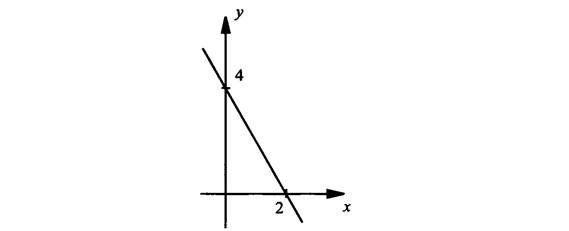
    Определить монотонность функции у(х) = – 2х + 4.

    Область определения этой функции – все значения х, т.е. х  (– ∞; + ∞). Возьмем два значения х из области определения этой функции х₁ и х₂ и пусть х₂ > х₁. Найдем значения функции в этих точках: у(х₁) = – 2х₁ + 4 и у(х₂) =  = – 2х₂ + 4. Теперь необходимо сравнить эти значения и определить, какое из них больше. Для этого рассмотрим разницу этих величин:

у(х₂) – у(х₁) = (– 2х₂ + 4) – (– 2х₁ + 4) = – 2х₂ + 4 + 2х₁ – 4 = – 2(х₂ – х₁).

    Так как х₂ > х₁, то разность х₂ – х₁ > 0 и величина – 2(х₂ – х₁) < 0. Поэтому получаем: у(х₂) – у(х₁) < 0, или у(х₂) < у(х₁). Это неравенство означает, что большему значению аргумента соответствует меньшее значение функции. Поэтому данная функция (по определению) является убывающей. Это же видно из приведенного графика функции.  

           Функция во всей области определения может быть немонотонной, но на отдельных промежутках функции может быть монотонной. Например, в примере 1 функция в целом немонотонная, но на промежутке х 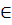 [3; + ∞) функция убывает, а на промежутке х  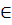(– ∞; 3] возрастает.

    И наконец, рассмотрим еще одно свойство функции – четность. Предварительно введем еще одно понятие – симметричность области определения. Область определения называется симметричной, если функция определена и в точке х₀ и в точке (– х₀) (т.е. в точке, симметричной х₀ относительно начала числовой оси). 

    Пример 4

    а) Областью определения функции 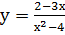являются все значения х, кроме тех, для которых х² – 4 = 0 (т.е. х = 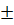2). Поэтому эта функция определена, например, как при х = – 1, так и при х = – (– 1) = 1.

    И наоборот, эта функция не определена и при х = – 2, и при х = – (– 2) = = 2. Следовательно, область определения данной функции:

х 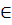 (– ∞; – 2)  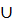(– 2; 2)  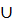(2; + ∞) симметричная.  

    б) Областью определения функции 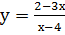 является все значения х, кроме тех, для которых х – 4 = 0 (т.е. х = 4). Поэтому эта функция определена в точке х = – 4, но не определена в симметричной точке х = – (– 4) = 4. Поэтому область определения данной функции х  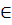(– ∞; 4)  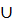(4; + ∞) не является симметричной.   

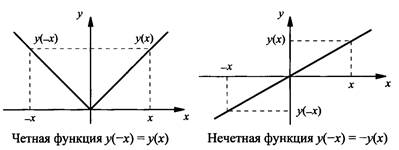
    Понятие четности функции вводится только для функции с симметричной областью определения. Функция называется четной, если при изменении знака аргумента, значение функции не меняется, т.е. у(– х) = у(х). График четной функции всегда симметричен относительно оси ординат. 

    Функция называется нечетной, если при изменении знака аргумента, значение функции также меняется на противоположное, т.е. у(– х) = – у(х). График нечетной функции всегда симметричен относительно начала координат.

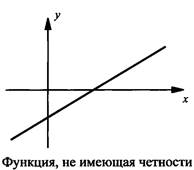
    На рисунке приведены (для наглядности) графики четной, нечетной функции и функции, не имеющей никакой четности.   

Пример 5

    Выяснить четность функций:

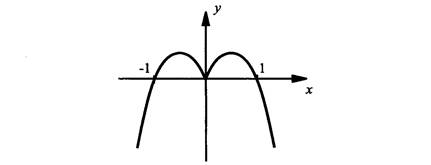
а) у = |х| – х².

у(– х) = |– х| – (–х)² = |х| – х² (здесь учтено, что |– х| = |х| и (–х)² = х²). Теперь легко видеть, что у(– х) совпадает с данной функцией у(х), т.е. у(– х) = у(х). Поэтому данная функция четная и ее график симметричен относительно оси ординат.

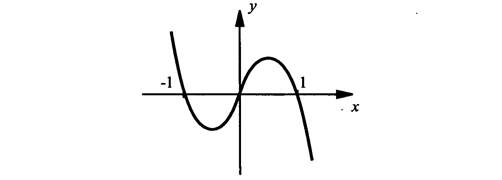
б) у = х – х³

у(– х) = – х – (– х)³ = – х + х³ = – (х – х³) = – у(х). Видно, что значения функции в точках х и – х противоположны по значению, т.е. у(– х) = – у(х). Поэтому данная функция нечетная и ее график симметричен относительно начала координат.   

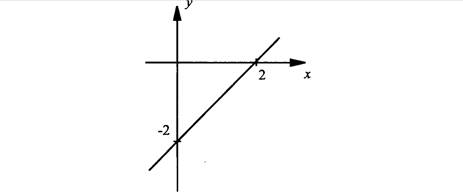
в) у = х – 2

у(– х) = – х – 2. Сравнивая значение – у(х) = – х – 2 со значением у(х) = х – 2, видим, что равенство у(– х) = у(х) не выполняется. Поэтому эта функция не является четной. Найдем теперь величину – у(х) = – (х – 2) = 2 – х. Сравнивая значения у(– х) = – х – 2 со значением – у(х) = 2 – х, видим, что равенство у(– х) = – у(х) также не выполняется. Поэтому эта функция не является нечетной.

    Итак, данная функция никакой четности не имеет и ее график не обладает никакой симметричности.   

     

Свойства и графики некоторых функций

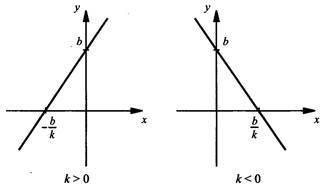
Линейная функция y = kx + b

1. Область определения – множество всех чисел

2. Графиком функции является прямая линия

3. График функции пересекает ось абсцисс в точке 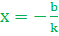 при (k ≠ 0) и параллелен оси абсцисс при k = 0. График функции пересекает ось ординат в точке у = b. 

4. Функция возрастает при k > 0, убывает при k < 0 и постоянна при k = 0.

5. Функция неограниченная при k ≠ 0 и ограниченная при k = 0.

6. Функция определенной четности не имеет при b ≠ 0 и у = b, нечетная при b = 0 и четная при k = 0. 

7. Область значений – множество всех чисел при k ≠ 0 и у = b при k = 0.

8. При b = 0 функцию у = kx называют прямой пропорциональностью.

     

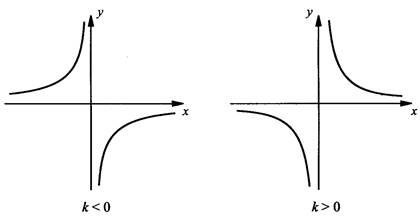
Обратная пропорциональность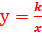

1. Область определения – множество всех чисел, кроме нуля. 

2. Графиком функции является гипербола

3. График функции осей координат не пересекает.

4. Функция возрастает при k < 0 и убывает при k > 0 в области определения.

5. Функция неограниченная

6. Функция нечетная

7. Область определений – множество всех чисел, кроме нуля.

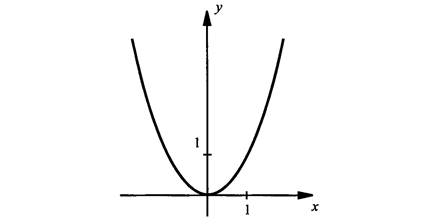
Квадратная функция у = х²

    Стоит отметить, что функция у = х² является частным случаем квадратичной функции, которая детально будет изучаться позднее.

1. Область определения – множество всех чисел

2. Графиком функции является парабола

3. График функции проходит через начало координат

4. Функция убывает на промежутке (– ∞; 0] и возрастает на промежутке [0; + ∞)

5. Функция ограничена снизу, т.е. у ≥ 0.

6. Функция нечетная

7. Область значений – промежуток [0; + ∞)

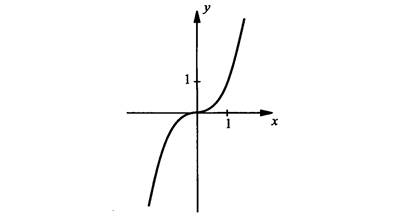
Кубическая функция у = х³

1. Область определения – множество всех чисел

2. График специального названия не имеет

3. График функции проходит через начало координат

4. Функция возрастает

5. Функция неограниченная

6. Функция нечетная

7. Область значений – множество всех чисел.

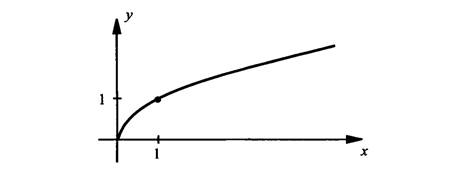
Функция у =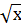

1. Область определения – множество неотрицательных чисел

2. График специального названия не имеет

3. График выходит из начала координат

4. Функция возрастает

5. Функция ограничена снизу, т.е. у ≥ 0

6. Функция определенной четности не имеет

7. Область значений – множество неотрицательных чисел

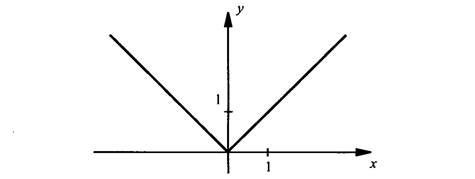
Функция у =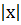

1. Область определения – множество всех чисел

2. График специального названия не имеет

3. График проходит через начало координат

4. Функция убывает на промежутке (– ∞; 0] и возрастает на промежутке [0; +∞)

5. Функция ограничена снизу, т.е. у ≥ 0

6. Функция четная

7. Область значений – множество неотрицательных чисел

---

Дата добавления: 2021-12-10; просмотров: 94; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!