Метод максимального правдоподобия.
ОТВЕТЫ НА ВОПРОСЫ
Что такое функция Лагранжа?
(в лекции 1 задача о линейной оценке с минимальной дисперсией)?
Решается задача на условный экстремум: найти минимум (или максимум)
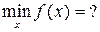
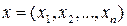
при условии 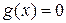
Решение (необходимое условие): составить функцию Лагранжа:
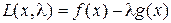
«двух» переменных 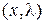 , и найти ее безусловный экстремум:
, и найти ее безусловный экстремум:
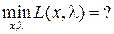
Необходимое условие:
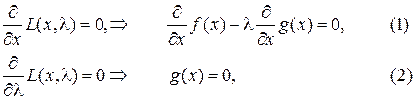
получаем, (1):
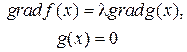
 Очень простой геометрический смысл этих уравнений при n=2
Очень простой геометрический смысл этих уравнений при n=2
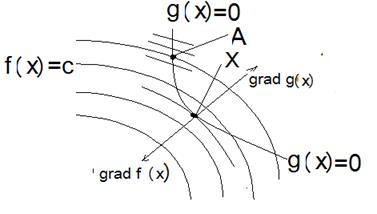
Точка А – не искомая точка: двигаясь по 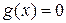 пересекаем линии уровня
пересекаем линии уровня 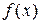 . Точка Х – искомая точка: двигаясь в ее окрестности,
. Точка Х – искомая точка: двигаясь в ее окрестности, 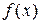 не меяется, потому что касание кривой
не меяется, потому что касание кривой 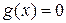 и
и 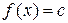
Что значит зависимость от параметра фиктивна?
(о неравенстве Рао-Крамера)
Утверждение. Эффективная оценка 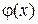 для
для 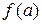 , если она существует, может быть представлена формулой
, если она существует, может быть представлена формулой
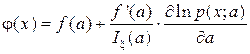 , (15)
, (15)
причем зависимость правой части от параметра а фиктивна.
Чем отличается усиленный ЗБЧ от ЗБЧ в форме Чебышева ?
ЗБЧ в форме Чебышева:
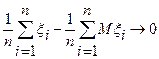 по вероятности при n®¥, (А)
по вероятности при n®¥, (А)
ЗБЧ усиленный
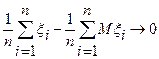 с вероятностью 1 при n ® ¥. (В)
с вероятностью 1 при n ® ¥. (В)
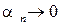 по вероятности при n ® ¥, т.е.
по вероятности при n ® ¥, т.е.
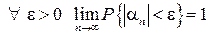
Короткое обозначение
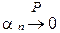
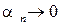 с вероятностью 1 при n ® ¥.
с вероятностью 1 при n ® ¥.
т.е.
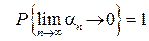
-------------------------
Сх-ть с вер 1 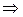 сх-ть по вер
сх-ть по вер
т.е
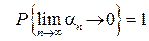
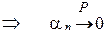 , обратное неверно
, обратное неверно
.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Лекция 4
Методы построения оценок
|
|
|
Рассмотрим лишь три наиболее популярных метода.
Метод моментов.
Пусть ξ1, ξ2…ξn - выборка,
т.е. n независимых наблюдений над случайной величиной, обозначим ее x0,
F(x; a1, а2…aR) -функция распределения, зависящая от неизвестных параметров a = (a1, а2… aR), всего R штук.
Требуется оценить их.
Идея метода: неизвестные параметры выразить через начальные моменты, а затем вместо моментов подставить несмещенные и состоятельные оценки моментов.
Выразим R моментов через R параметров:
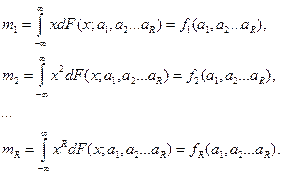 , j = 1, 2…R. (1)
, j = 1, 2…R. (1)
Пусть из этой системы равенств можно выразить параметры через моменты:
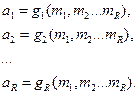 j = 1, 2…R. (2)
j = 1, 2…R. (2)
Подставив вместо моментов m1,m2… mR оценки моментов 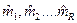 , получаем:
, получаем:
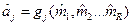 , где
, где 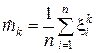 , k = 1, 2…R.
, k = 1, 2…R.
Мы получили некоторые оценки 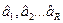 ; они называются оценками по ММ.
; они называются оценками по ММ.
Справедливы следующие свойства (см., например, [1], [3]):
1) если функции gj ( × ), j = 1, 2...R, непрерывны, то оценки состоятельны;
2) если функции gj( × ), j = 1, 2...R, дифференцируемы, а распределение при любом a имеет 2R моментов, то оценки 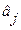 асимптотически нормальн :
асимптотически нормальн : 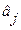 ~ N (aj,
~ N (aj, 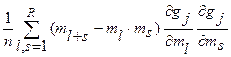 .
.
В справедливости этих свойств нетрудно убедиться.
Несмещённость оценок не гарантируется.
Что такое асимптотическая нормальность? Если закон распределения оценки с ростом n стремится к нормальному, то говорят, что оценка асимптотически нормальна.
|
|
|
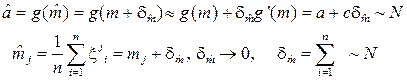
Замечания.
1. В равенствах (1) вместо первых R моментов можно использовать любые R моментов; важно лишь, чтобы система была разрешима относительно параметров.
2. Моментные оценки не всегда обладают высокой точностью. Однако, обычно они достаточно просты в вычислительном отношении.
Пример 1. Оценим дисперсию s2 методом моментов. Дисперсия s2 выражается через первые два момента:
s2 = 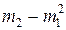 .
.
Подставив оценки моментов, получим оценку s2 для дисперсии 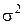 :
:
s2 = 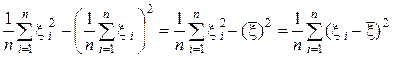 . (3)
. (3)
Последнее равенство нетрудно проверить:
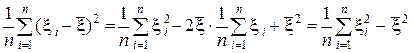 .
.
Оценка (3) совпадает с оценкой s2, которая была проанализирована в разделе 2.3.
Пример 2. Оценка параметров равномерного распределения.
Пусть x1, ξ2…xn — выборка из совокупности, распределенной по равномерному закону R[a, b] на отрезке [a, b]. Оценим два неизвестных параметра a и b. Первые два момента выражаются через два параметра:
m1 = (a + b) / 2,
m2 - m12 = s2 = (b – a)2 / 12.
В этих уравнениях относительно a и b заменяем неизвестные моменты выборочными, при этом во втором уравнении слева, исходя из (3), имеем s2. Получаем:
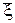 = (a + b) / 2,
= (a + b) / 2,
|
|
|
s2 = (b – a)2 / 12.
 = 2
= 2 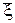 ,
,
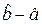 =2
=2 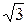 s.
s.
Откуда:
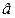 =
= 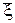 –
– 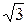 s,
s, 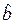 =
= 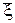 +
+ 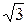 s.
s.
Метод максимального правдоподобия.
Пусть x1, ξ2…xn — выборка, q(xi; a) — плотность распределения одного i-го наблюдения (в дискретном случае q(xi; a) — вероятность принятия дискретного значения xi), a = (a1, а2…aR) — неизвестный параметр,
px(x;a) = 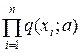 — распределение выборки x = (x1, х2…x n ).
— распределение выборки x = (x1, х2…x n ).
Функция px( x;a), как функция параметра а, при фиксированном х, называется функцией правдоподобия.
Оценкой максимального правдоподобия (мп оценкой) а* параметра а называется такое значение, при котором функция правдоподобия px( x; a) достигает максимума:
а*: p x( x; a*) = 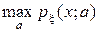 . (4)
. (4)
Если максимум достигается во внутренней точке области определения функции, то а* удовлетворяет системе уравнений:
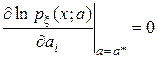 , i = 1, 2…R. (4а)
, i = 1, 2…R. (4а)
Использование логарифма не изменяет точки максимума, но упрощает выкладки при независимых наблюдениях. Оценка а*= а*(x) является функцией наблюдений x. Чтобы подчеркнуть случайность аргумента, напишем а*(x).
Пример 1. МП оценка параметров нормального распределения.
Пусть x1, ξ2…xn — выборка из нормальной совокупности N(m, s2), здесь а º (m, s2). Параметры m и s2 неизвестны. Плотность распределения выборки:
|
|
|
px(x; m,s2) = 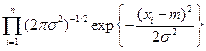 .
.
Логарифм функции правдоподобия:
ln px(x; m, s2) = 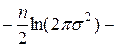
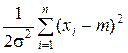 .
.
Система уравнений для определения оценок:
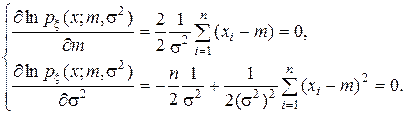
Из первого уравнения находим
m* = 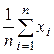 º
º 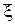 . (5)
. (5)
Из второго уравнения находим
(s2)* = 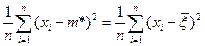 . (6)
. (6)
В данном случае оценки совпадают с выборочными средним и дисперсией.
Пример 2. МП оценка параметра равномерного распределения.
Пусть x1, ξ2…xn — выборка из совокупности, распределенной по равномерному закону R[0, a] с неизвестным правым концом a > 0. Плотнсть распределения для одного наблюдения с номером i:
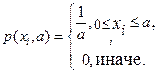
Плотность распределения выборки x
px(x1, х2…xn ; a) = 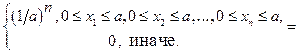
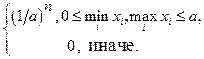
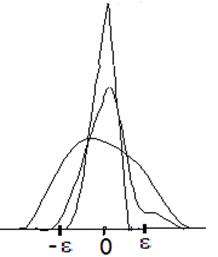
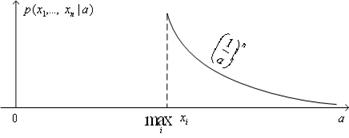 При фиксированных x1, х2…xn функция правдоподобия убывает
При фиксированных x1, х2…xn функция правдоподобия убывает 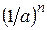 при
при 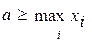 и равна 0 при а <
и равна 0 при а < 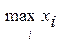 (рис. 2). Максимум достигается при
(рис. 2). Максимум достигается при
а* = 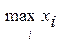 .
.
Рис. 2. Функция правдоподобия
Проанализируем эту оценку. Ее функция распределения:
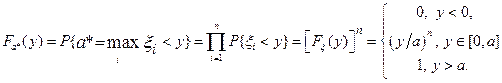
Плотность распределения:
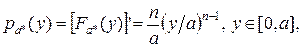 иначе 0.
иначе 0.
Математическое ожидание:
Mа*= 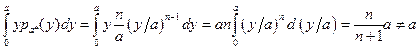 ,
,
т.е. оценка смещенная.
Оценку легко исправить, т.е. сделать несмещенной, умножив ее на 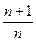 , в результате чего получим оценку
, в результате чего получим оценку
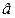 =
= 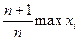 .
.
Она уже несмещенная. Ее второй момент
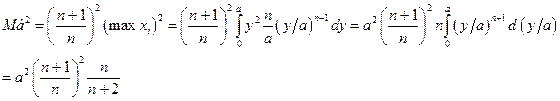
 Дисперсия
Дисперсия
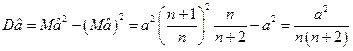
Из вышесказанного видно, что дисперсия убывает быстрее, чем 1/n, что противоречит неравенству (14) раздела 3.2. Однако, в этом примере условия неравенства Рао-Крамера не выполняются, а именно, условие 1 о независимости носителья вероятности от параметра. Дисперсия может убывать быстрее, и это пример сверхэффективной оценки.
Свойства оценок максимального правдоподобия.
Пусть x º (x1, ξ2…xn) — выборка объема n из совокупности, распределенной с плотностью q(x;a),ивыражение
p(x1, х2 ...xn ;a) = 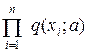 (7)
(7)
является плотностью распределения выборки.
При некоторых весьма широких условиях (см. ниже) оценки максимального правдоподобия:
— состоятельны;
— асимптотически эффективны;
— асимптотически нормальны.
Для одномерного случая:
Mа * ® а, Dа *® 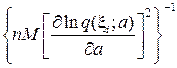 =
= 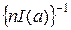 при n ® ¥ . (8)
при n ® ¥ . (8)
условия, при которых вышеприведенные свойства верны, совпадают с условиями неравенства Рао-Крамера:
а) независимость от параметра а множества X = {x: q(x/a) ¹ 0}- носителя вер-ти;
б) существование производных 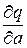 и
и 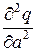 ;
;
в) существование интеграла 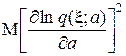 .
.
Доказательство справедливости этих свойств можно найти, например, в [5]. Примем на веру состоятельность и покажем, как возникает асимптотическая эффективность и асимптотическая нормальность.
Рассмотрим случайную функцию от а
Sn(a ,x) = 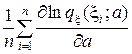 . (9)
. (9)
Учитывая (4а) 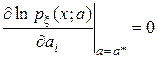 определение МП-оценки
определение МП-оценки
и (7) p(x1, х2 ...xn ;a) = 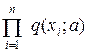 (7)
(7)
ясно, что оценка а* является корнем этой случайной функции от параметра а
Sn(а*,x) = 0.
Пусть а0 — истинное значение параметра. Рассмотрим
Sn(а,x) - случайную величину в точке истинного значения параметра а = а0. Учитывая состоятельность,
т.е. а* ® а0,
и гладкость функции Sn(a ,x), по теореме Лагранжа имеем:
Sn(а0,x) = Sn(а*,x) + (а0 – а*) S ’n( 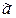 ,x), (10)
,x), (10)
где 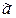 — промежуточная точка между а0 и а*, причем
— промежуточная точка между а0 и а*, причем 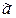 ® а0.
® а0.
В силу предыдущего уравнения, справа первое слагаемое равно 0. Умножим это соотношение на 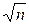 :
:
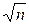 Sn(а0,x) =
Sn(а0,x) = 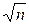 (а0- а*) S ’ n(
(а0- а*) S ’ n( 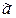 ,x), (11)
,x), (11)
Слева имеем случайную величину
z= 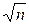 Sn(а0,x),
Sn(а0,x),
которая, учитывая суммирование случайных величин в (9), асимптотически нормальна N(0, I(a0)) с параметрами: М.О.
Mz = 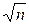 MSn(а0,x) =
MSn(а0,x) = 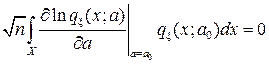 .
.
При вычислении интеграла учтено, что
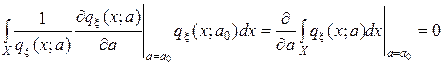 .
.
Что касается дисперсии, то она равна информации Фишера в одном наблюдении в точке а0: действительно
Dz = 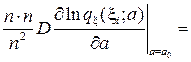
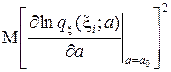 = I(a0).
= I(a0).
Теперь определим параметры случайной величины S ’ n( 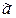 ,x) в правой части (11) при n ® ¥ с учетом того, что
,x) в правой части (11) при n ® ¥ с учетом того, что 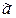 ® а0:
® а0:
MS ’ n( 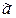 ,x) =
,x) = 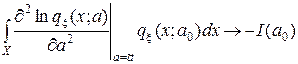 ,
,
DS ’ n( 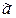 ,x) =
,x) = 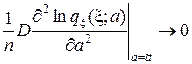 .
.
Это означает, что S ’ n( 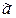 ,x) сходится к константе I(a0). Из (11) в пределе получаем
,x) сходится к константе I(a0). Из (11) в пределе получаем
z= - 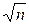 (а0 - а*)
(а0 - а*) 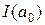 ,
,
что означает, выразив а* через z:
а* = а0 + 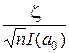 .
.
Из этого следует, что оценка а* асимптотически нормальна, а дисперсия {nI(a0)}-1. Это значение совпадает с границей Рао-Крамера.
Замечания.
1. Эффективная оценка, если она существует, является оценкой максимального правдоподобия.
Действительно, если j(x) — эффективная оценка для параметра a, то по лемме из раздела 3.3 имеем
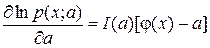 ,
,
откуда, приравнивая производную к нулю, получаем 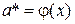 .
.
2. Оценка максимального правдоподобия является функцией достаточной статистики, если последняя существует.
Действительно, если T(x) — достаточная статистика, то в силу критерия факторизации в разделе 4.2 справедливо представление
p(x;a) = g(T(x), a)h(x),
и потому
 p(x;a) = h(x)×
p(x;a) = h(x)×  g(T(x), a),
g(T(x), a),
откуда экстремальная точка a* = a*[(T(x)].
Метод порядковых статистик.
В статистике широко используется система числовых характеристик, называемых квантилями.
Значение xp случайной величины x называется p-квантилью, если
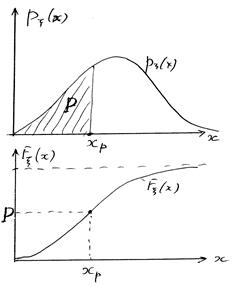 P{x< xp} = p,
P{x< xp} = p,
где xp — это корень уравнения
Fx(xp) = p
(рис. 3).
Примеры р-квантили:
x0,5 — медиана — характеристика среднего значения случайной величины;
x0,98 — максимальное, в некотором смысле, значение случайной величины, т.к. P{x < x0,98} = 0,98;
x0,02 — минимальное, в некотором смысле, значение случайной величины, т.к. P{x ³ xp} = 1 – P{x < xp} = 1– p = 0,98;
x3/4 и x1/4 — верхняя и нижняя квартили; их разность(x0,75 – x0,25) — межквартильная широта — служит характеристикой разброса.
Рис. 3. Графическая иллюстрация квантили xp
Оценка p-квантилей . Неизвестные p-квантили легко оцениваются по выборке. Действительно, пусть
x1, х2...xn — результаты n независимых наблюдений над случайной величиной x с функцией распределения F(x). Упорядочив их по возрастанию, получаем вариационный ряд
x(1) £ x(2) £ ... £ x(n).
Чтобы подчеркнуть случайность ряда, запишем его греческими символами
x (1) £x (2) £ ... £ x(n).
член вариационного ряда x (i) с номером i (заметим, что это случайная величина) называется i-й порядковой статистикой. по вариационному ряду построим функцию 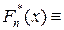
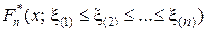 эмпирического распределения, и, согласно общему принципу о том, что выборочные характеристики являются состоятельными оценками характеристик распределения генеральной совокупности, рассмотрим в качестве оценкидля p-квантили xp выборочную квантиль z p, т.е. корень уравнения
эмпирического распределения, и, согласно общему принципу о том, что выборочные характеристики являются состоятельными оценками характеристик распределения генеральной совокупности, рассмотрим в качестве оценкидля p-квантили xp выборочную квантиль z p, т.е. корень уравнения
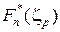 = p. (8)
= p. (8)
Поскольку 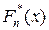 — функция кусочно-постоянная, то корнем является одна из порядковых статистик
— функция кусочно-постоянная, то корнем является одна из порядковых статистик
zp = x ([np]+1), (9)
с номером [np]+1, т.е. целая часть числа np плюс 1(рис. 4).
 Нетрудно показать, что zp является состоятельной оценкой для xp . Кроме того, известна теорема Крамера, которая гласит, что
Нетрудно показать, что zp является состоятельной оценкой для xp . Кроме того, известна теорема Крамера, которая гласит, что
для непрерывных распределений с плотностью q(x) оценка zp асимптотически нормальна с параметрами:
Рис. 4. Графическая иллюстрация выборочной квантили
Mzp = xp, Dzp = 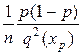 . (10)
. (10)
Метод оценки параметров основан на оценках zp при разных p. Пусть x1, x2…xn — выборка с функцией распределения F(x;a), зависящей от параметра a, значение которого требуется оценить. Выберем р так, чтобы квантиль xр зависела от параметра:
xр = f(a).
Выразим параметр а через квантиль xр:
а = g(xр),
и вместо xр подставим выборочную квантиль zp = x([np]+1), в результате чего получим состоятельную оценку
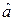 = g(x ([np]+1)).
= g(x ([np]+1)).
Таким же образом можно построить оценки и для неодномерного параметра.
Основное и очень важное преимущество оценок, основанных на порядковых статистиках, — их устойчивость к засорению наблюдений и к изменениям закона распределения.
Примеры оценок параметров нормального распределения.Пусть x1, x2…xn — выборка из нормальной совокупности N(m, s2).
1) Оценка среднего m . Известно или нет значение s — безразлично. В силу симметрии нормального распределения параметр m является медианой, т.е. квантилью уровня ½, и потому может быть оценен выборочной медианой:
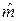 = z½ = x([n/2]+1).
= z½ = x([n/2]+1).
Можно сравнить по точности эту оценку с эффективной оценкой
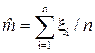
с дисперсией 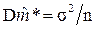 .
.
согласно n (10), теореме Крамера, D 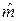 »
» 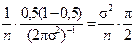 ,
,
т.е. очень простая и устойчивая к засорению оценка 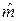 уступает по точности оценке
уступает по точности оценке 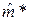 в
в 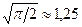 раза, т.е. 25 %.
раза, т.е. 25 %.
2) Оценка стандартного уклонения s.
Легко проверить, что верхняя и нижняя квартили равны соответственно x3/4 = m + 0,675s и x1/4= m – 0,675s, т.к.
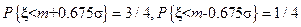
И потому
s = (x3/4 - x1/4) / 1,35,
и потому оценивать s можно следующим образом:
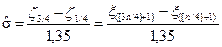 .
.
3) Оценка стандартного уклонения s по размаху.
Пусть x (1) и x (n) — минимальный и максимальный член выборки, разность которых называется размахом w:
w = x (n) – x (1).
Ясно, что Mw = c(n)s, и потому оценкой для s может служить
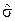 = w/c(n) = k(n)w,
= w/c(n) = k(n)w,
где k(n) берем из статистических таблиц [4]. Ниже приведены значения коэффициента k(n)и коэффициента эффективности
e ff = 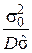 , где
, где 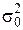 — нижняя граница Рао-Крамера,
— нижняя граница Рао-Крамера,
а также потеря точности
(1– 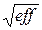 ) ∙ 100,
) ∙ 100,
измеряемая в процентах, по сравнению с нижней границей Рао-Крамера.
Табл. 1. Значение коэффициентов k и n
| n | 2 | 5 | 10 |
| k(n) | 0,866 | 0,430 | 0,325 |
| eff | 1,000 | 0,955 | 0,855 |
потеря точности, (1 – 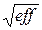 )100, % )100, %
| 0 | 2,5 | 7 |
Для устойчивости оценки к засорению используют подразмахи wm порядка m , где m = 1, 2, 3…:
wm = x (n- m +1) - x (m),
так что оценка имеет вид:
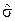 = k m(n) w m.
= k m(n) w m.
Значение коэффициента k m(n) берется из таблиц.
4) Распределение порядковых статистик . При анализе оценок, получаемых рассматриваемым методом, необходимо знать распределения порядковых статистик. Если распределение одного наблюдения x непрерывно с плотностью p(x) = F ’(x), топлотность распределения для k-й порядковой статистики x (k) выражается следующей формулой:
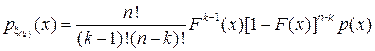 ,
,
которая получается вычислением вероятности события
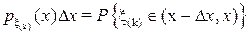 ,
,
означающего, что при n-кратном испытании случайной величины x событие 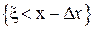 ,вероятность которого
,вероятность которого 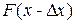 , появится (k-1) раз, событие
, появится (k-1) раз, событие 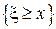 , вероятность которого (
, вероятность которого ( 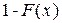 ), появится (n-k) раз, и событие
), появится (n-k) раз, и событие 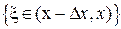 , вероятность которого
, вероятность которого 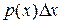 , появится 1 раз.
, появится 1 раз.
Дата добавления: 2021-12-10; просмотров: 80; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
