Примеры и разбор решения заданий тренировочного модуля
Преподаватель - Брыкало А.А.
brukalo_aa@mail.ru
https://vk.com/id399759339
Конспект урока «Математики»
Группа 99 «Мастер по ремонту и обслуживанию автомобилей»
Курс 1
Тема урока «Показательные неравенства»
Форма работы: индивидуальная, дистанционное обучение.
Тип урока: урок изучения нового материала.
Цель урока: формировать систему знаний и умений, связанных с решением показательных неравенств
Ключевые слова: показательные неравенства , метод интервалов, замена.
Изучаемая литература: Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.
10-11 классы: учеб.дляобщеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г
Интернет- ресурсы : Математика в открытом колледже http://www.mathematics.ru
http://school-collection.edu.ru/ - Единая коллекция цифровых образовательных ресурсов
Ход занятия :
Организационный этап. Мотивационный модуль
Ребята, сегодня, вы познакомитесь с темой «Показательные неравенства, рассмотрите примеры решения показательных неравенств
Основная часть. Объясняющий модуль.
План изучения:
· простейшие показательные неравенства;
· решение показательных неравенств замена переменной, разложение на множители;
· метод рационализации при решении показательных неравенств;
· метод интервалов при решении показательных неравенств;
|
|
|
· графический метод решения показательных неравенств.
1. Рассмотрим показательные неравенства.
Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.
Неравенства вида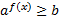 
, 
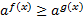называются простейшими показательными неравенствами.
В самом простом случае неравенство принимает вид: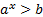 
., знак неравенства может быть любым (<, >, 
, 
).
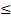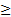Множество решения неравенства будет зависеть и от знака неравенства, и от основания степени, и от значения b.
Так как множество значений показательной функции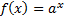 
– множество положительных чисел, то при 
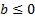неравенства: 
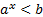и 
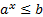решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств 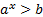и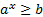 
является все множество действительных чисел, независимо от значения основания а (см. Рисунок 1).
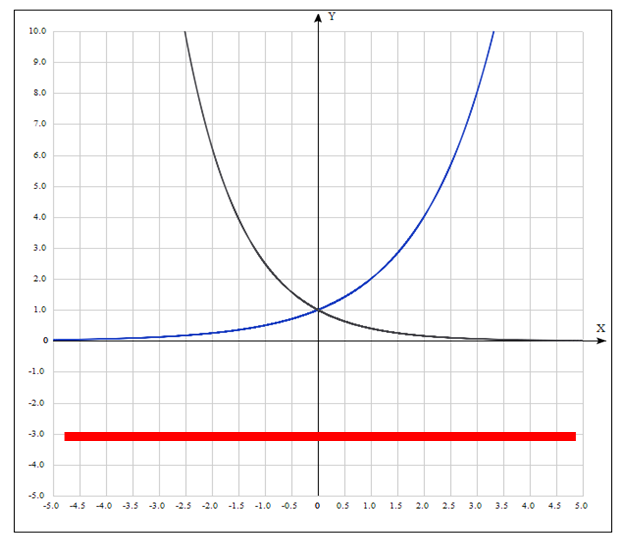
Рисунок 1 – иллюстрация решения простейшего показательного неравенства при b<0
Теперь рассмотрим случай b>0, a>1.
В том случае, когда основание степени a>1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства не изменяется (см. Рисунки 2 и 3).
|
|
|
Рисунок 2 – иллюстрация решения простейшего показательного неравенства 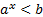или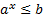 
при b>0, a>1.
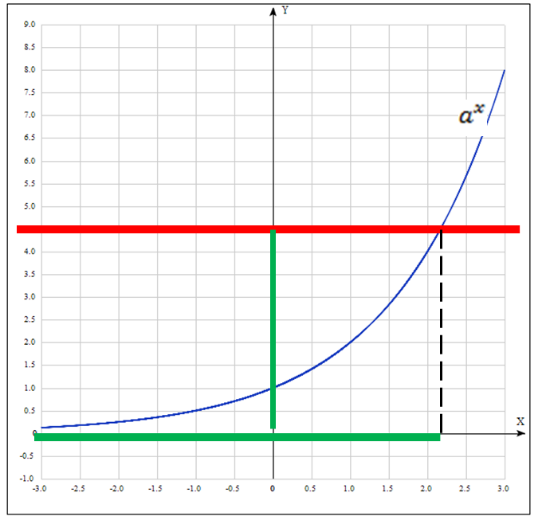
· Рисунок 3 – иллюстрация решения простейшего показательного неравенства 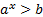или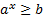 
при b>0, a>1.
· Теперь рассмотрим случай b>0, 0<a<1.
· В том случае, когда основание степени 0<a<1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства изменяется на противоположный (см. Рисунки 4 и 5).
· 
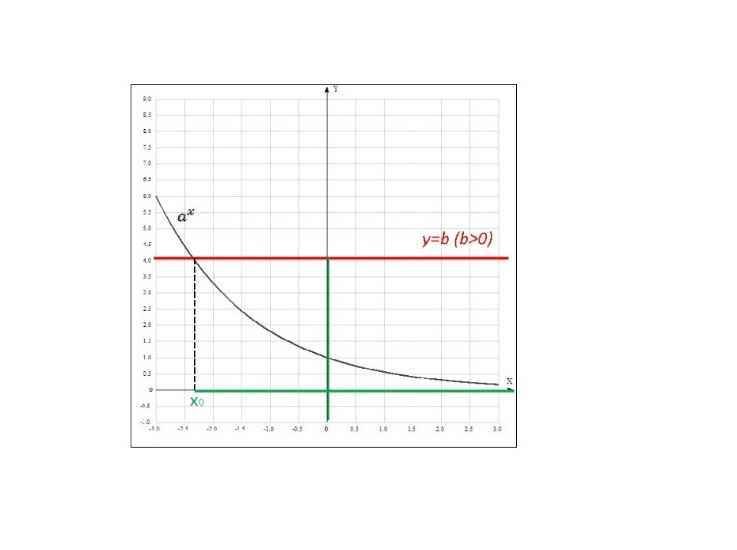
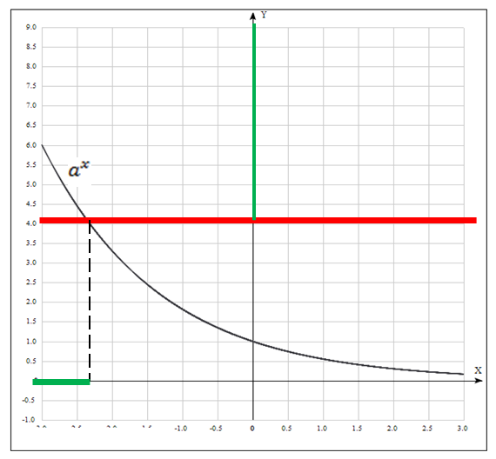
· Рисунок 4 – иллюстрация решения простейшего показательного неравенства 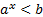или 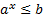при b>0, 0<a<1.
· 
· Рисунок 5 – иллюстрация решения простейшего показательного неравенства 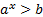или 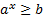при b>0, 0<a<1.
· Для того чтобы решить простейшее показательное неравенство 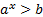, нужно число b представить в виде степени числа a.
· Рассмотрим пример: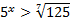 
.
Представим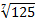 
в виде степени числа 5: 
.
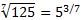Теперь перепишем данное неравенство в виде: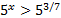 
.
Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, поэтому x>3/7.
Ответ: x>3/7.
· Рассмотрим еще один пример: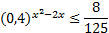 
.
Перепишем его в виде
.
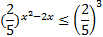Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменяется на противоположный:
,
,
.
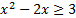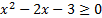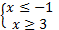Ответ: .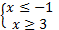
|
|
|
2.Закрепление .
Примеры и разбор решения заданий тренировочного модуля
1. 
.
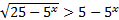Решение:
Введем новую переменную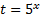 
.
Запишем вспомогательное неравенство: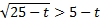 
.
1) Если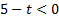 
, то решением неравенства является любое значение t, которое удовлетворяет области определения: 
.
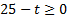Решив систему: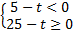 
, получаем: 
.
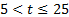2) Если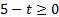 
( 
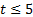), возведем обе части неравенства в квадрат:
.
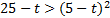Решим его: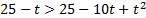 
,
,
,
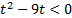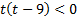0<t<9.
Учитывая условие 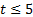, получаем: 
.
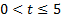Таким образом, объединяя первый и второй случай, получаем решение иррационального вспомогательного неравенства:
.
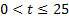Вернемся к исходной переменной:
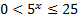. Так как 
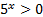всегда, то получаем: 
.
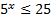Учитывая, что основание степени больше 1, получаем:
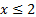
Ответ: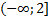 
.
2. (x^2+x+1)^((x+5)/(x+2))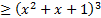 
Решение:Используем метод рационализации и перепишем неравенство в виде:
,
.
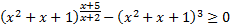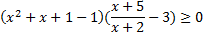Получили неравенство: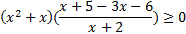 
.
Упростим его и решим методом интервалов:
,
.
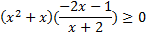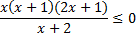Ответ: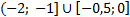 
.
Домашнее задание 1.Составьте краткий конспект
2.Контрольное задание:
Решите неравенство: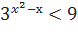 
Конспект и выполненное контрольное задание отправить личным сообщением в ВК
Дата добавления: 2021-12-10; просмотров: 22; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!