Способ 4. Графический способ решения.

Способ 1. Решение по определению логарифма.

Логарифмом положительного числа х по основанию 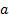,  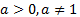называется показатель степени b, в которую надо возвести 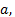чтобы получить х.

 

log_a х=b – это одно и тоже, что и a ^b = x

 

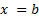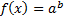Если , то (где, a > 0, a ≠ 1,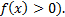

Пример 1.

log₂ (x+2) = 4

Воспользуемся определением логарифма

x+2 = 2⁴

x+2 = 16

x = 16-2

x=14

Проверка: для проверки подставляем полученный корень только в подлогарифмические выражения (x+2)=14+2=16 >0, условие выполнено. Корень подходит.

Ответ: 14.

Пример 2.

log₂ (x+1) + log₂ (x+3) = 3

Здесь необходимо использовать свойства логарифмов: log_a b + log_a c = log_a (b*c)

log₂ (x+1)*(x+3) = 3

Воспользуемся определением логарифма

(x+1)*(x+3) = 2³

(x+1)*(x+3) = 8

x²+x+3x+3=8

x²+4x-5=0

x₁=1, x₂=-5.

Проверка: для проверки подставляем полученные корни только в подлогарифмические выражения

Для первого корня x₁=1:

(x+1)=1+1=2 >0

(x+3)=1+3=4 >0

Корень подходит.

Для второго корня x₂=-5:

(x+1)=-5+1=-4 <0

(x+3)=-5+3=-2 <0

Корень не подходит, так как выражение меньше нуля.

Ответ: 1.

 

Пример 3.

log₄ (x+6) - log₄ (x) = 1

Здесь необходимо использовать свойства логарифмов: log_a b - log_a c = log_a (b/c)

log₄ (x+6)/x = 1

Воспользуемся определением логарифма

(x+6)/x = 4¹

(x+6)/x = 4

По свойству пропорции находим:

x+6=4x

x-4x=-6

-3x=-6

x=2

Проверка: для проверки подставляем полученные корни только в подлогарифмические выражения

(x+6)=2+6=8 >0

(x)=6 >0

Корень подходит.

Ответ: 2.

 

Способ 2. Решение по свойству логарифмов:

если два логарифма с одинаковыми основаниями равны, то знаки логарифмов можно опустить. Т.е. если log_a b = log_a c , то b = c .

 

Если log_a x₁ = log_a x₂,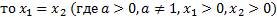

Если log_a f(x) = log_a g(x),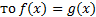

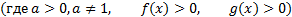
Пример 4.

log₄ (x²) = log₄ (2x-1)

x² = (2x-1)

x² – 2x+1=0

x=1

Проверка:

(x²)=1²=1 >0

(2x-1)=2*1-1=1 >0

Корень подходит.

Ответ: 1.

 

Пример 5 .

log₁₅ (2x²–4x+12) = log₁₅ (x) + log₁₅ (x+3)

Справа используем свойство логарифмов:

log₁₅ (2x²–4x+12) = log₁₅ (x*(x+3))

Опускаем логарифмы:

(2x²–4x+12) = (x*(x+3))

2x²–4x+12= x²+3x

2x²–4x+12– x²–3x=0

x²–7x+12=0

x₁=3, x₂=4.

Проверка: для проверки подставляем полученные корни только в подлогарифмические выражения

Для первого корня x₁=3:

(2x²–4x+12)= 2*3²–4*3+12=18 >0

(x)=3 >0

(x+3)=3+3=6 >0

Корень подходит.

Для второго корня x₂=4:

(2x²–4x+12)= 2*4²–4*4+12=28 >0

(x)=4 >0

(x+3)=4+3=7 >0

Корень подходит.

Ответ: 3,4.

 

Способ 3. Введение новой переменной.

Пример 6 .

log₅² (x) + 4*log₅ (x) – 5 = 0

Замена: log₅ (x) = t, тогда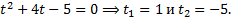

Возвращаем замену обратно для каждого из полученных корней:

log₅ (x) = 1

Решаем уравнение по определению логарифма:

x = 5¹

x = 5

log₅ (x) = -5

Решаем уравнение по определению логарифма:

x = 5^-5

x = 1/3125

Проверка: для проверки подставляем полученные корни только в подлогарифмические выражения

Для первого корня x₁=5:

(x)=5 >0

Корень подходит.

Для второго корня x₂=1/3125:

(x)= 1/3125 >0

Корень подходит.

Ответ: 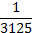; 5.

 

Пример 7.

log₃ (x) + log_x (3) = 5/2

Замена: log₃ (x) = t, тогда log_x (3) = 1/t в силу свойств логарифма.

Тогда

t+1/t=5/2

(t²+1)/t=5/2

Псвойству пропорции:

2*(t²+1)=5*t

2t²+2=5t

2t²-5t+2=0

t₁=2, t₂=1/2.

Возвращаем замену обратно для каждого из полученных корней:

log₃ (x) = 2

Решаем уравнение по определению логарифма:

x = 3²

x = 9

log₃ (x) = 1/2

Решаем уравнение по определению логарифма:

x = 3^1/2

Проверка: для проверки подставляем полученные корни только в подлогарифмические выражения

Для первого корня x₁=9:

(x)=9 >0

Корень подходит.

Для второго корня x₂=3^1/2:

(x)= 3^1/2>0

Корень подходит.

Ответ: 9, 3^1/2.

 

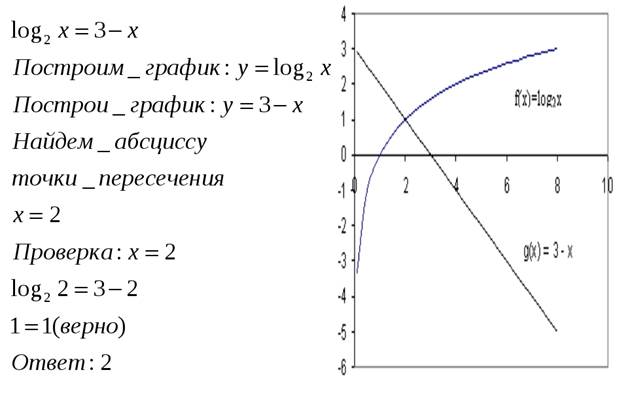
Способ 4. Графический способ решения.

Строим графики левой и правой частей уравнения, определяем абсциссы точек пересечения графиков.

 

Пример 8.

 

---

Дата добавления: 2021-12-10; просмотров: 71; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!