Комбинированный метод (хорд и касательных)
Пусть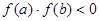 
, а 
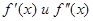сохраняют постоянные знаки на отрезке [a,b]. Соединяя способ пропорциональных частей и метод Ньютона, получаем метод, на каждом этапе которого находим значения по недостатку и по избытку точного корня ξ уравнения f(x)=0 . Теоретически здесь возможны 4 случая:
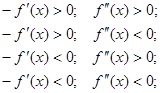
Соединим точки А(а, f(а)) и B(b, f(b)) хордой, а касательную будем проводить из точки В. Тогда расчетные формулы имеют вид:
;
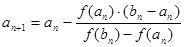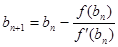, n=0, 1, 2,…
Процесс сближения прекращается, если выполнено условие:
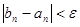
Корень уравнения есть среднее арифметическое последних полученных значений
.
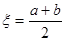Метод простых итераций
Пусть дано уравнение f(x)=0, где f(x) – непрерывная функция, и требуется определить его вещественные корни. Заменим исходное уравнение равносильным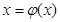 
(1)
С этой целью умножим функцию f(x) на постоянный множитель λ и прибавим к левой и правой частям уравнения, т.е. :
Х + λ f(x) = Х
Обозначив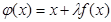 
, приведем к виду (1). Выберем начальное приближение к корню х и подставим его в правую часть уравнения. Получим новое приближение 
.
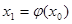Повторяя этот процесс, будем иметь последовательность чисел:
…….
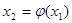
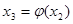
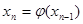, n=1,2,3,….
Если эта последовательность – сходящаяся, т.е. существует предел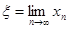 
, то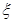 
является корнем уравнения.
Вычислительный процесс заканчивается при выполнении условия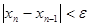 
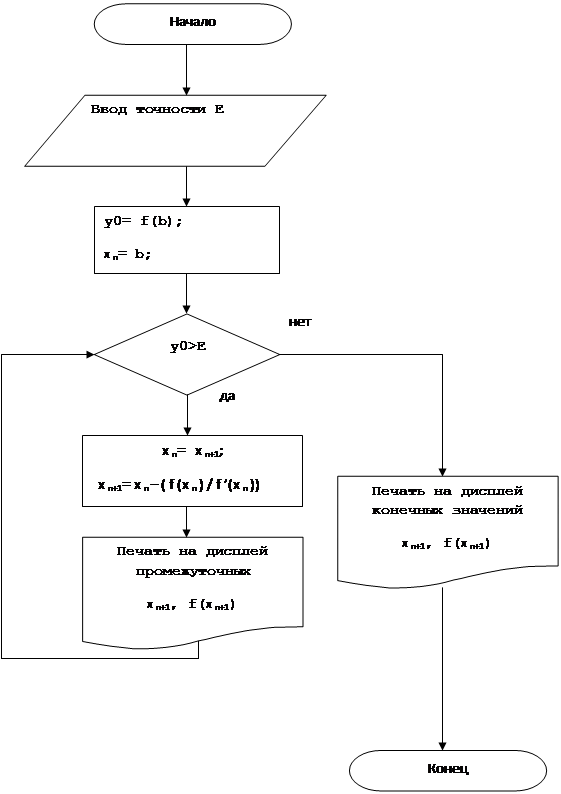
Блок-схема метода касательных ( Ньютона)
Блок-схема, соответствующая алгоритму решения задачи
|
|
|
Программа на языке Паскаль
Program 1a;
Var
X0,xn,xk: real;
Const
E=0.0001;
Function f(x: real): real;
Begin
F:=2*x*x-cos(3.14*x)/(3*sin(3.14*x));
End;
Begin
writeln (‘Введите начальное приближение x0’);
readln (x0);
xn:=x0;
xk:=f(x0);
while abs(xk-xn)>=e do
begin
xn:=xk;
xk:=f(xn);
end;
writeln (‘Искомое решение’, xk);
End.
Решение задачи №4
Формулировка: найти наименьший положительный корень уравнения с точностью e=10-4 методом касательных.
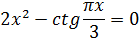
Отделим корень уравнения графически.
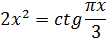
Корень принадлежит отрезку [0,2; 0,4].
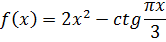
Вычислим: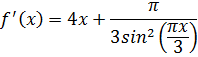 
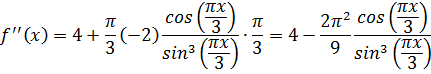
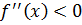
Выбираем конец a, так как f(a)<0.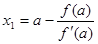 
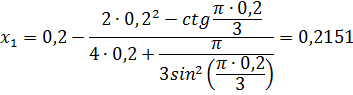
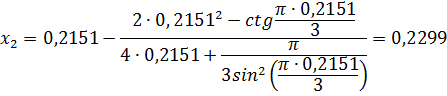
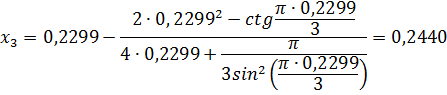
Найдем разность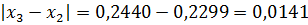 
Далее воспользуемся программой MS Excel.
|
| x | F(x) | F'(x) | x1 | Разность | ||
| 1 шаг | 0,2 | -0,37879 | 25,02539 | 0,215136 | 0,015136 | ||
| 2 шаг | 0,215136 | -0,32314 | 21,84529 | 0,229928 | 0,014792 | ||
| 3 шаг | 0,229928 | -0,27253 | 19,33571 | 0,244023 | 0,014095 | ||
| 4 шаг | 0,244023 | -0,227 | 17,36627 | 0,257094 | 0,013071 | ||
| 5 шаг | 0,257094 | -0,1866 | 15,82986 | 0,268882 | 0,011788 | ||
| 6 шаг | 0,268882 | -0,15136 | 14,63851 | 0,279222 | 0,01034 | ||
| 7 шаг | 0,279222 | -0,1212 | 13,72017 | 0,288056 | 0,008834 | ||
| 8 шаг | 0,288056 | -0,09588 | 13,01619 | 0,295423 | 0,007366 | ||
| 9 шаг
| 0,295423 | -0,07503 | 12,47922 | 0,301435 | 0,006013 | ||
| 10 шаг | 0,301435 | -0,05817 | 12,0714 | 0,306254 | 0,004818 | ||
| 11 шаг | 0,306254 | -0,04473 | 11,76281 | 0,310057 | 0,003803 | ||
| 12 шаг | 0,310057 | -0,03418 | 11,52999 | 0,313021 | 0,002964 | ||
| 13 шаг | 0,313021 | -0,02597 | 11,35476 | 0,315308 | 0,002288 | ||
| 14 шаг | 0,315308 | -0,01966 | 11,22312 | 0,31706 | 0,001752 | ||
| 15 шаг | 0,31706 | -0,01483 | 11,12438 | 0,318393 | 0,001333 | ||
| 16 шаг | 0,318393 | -0,01116 | 11,0504 | 0,319403 | 0,00101 | ||
| 17 шаг | 0,319403 | -0,00838 | 10,99501 | 0,320165 | 0,000762 | ||
| 18 шаг | 0,320165 | -0,00629 | 10,95358 | 0,320739 | 0,000574 | ||
| 19 шаг | 0,320739 | -0,00471 | 10,9226 | 0,32117 | 0,000431 | ||
| 20 шаг | 0,32117 | -0,00352 | 10,89944 | 0,321493 | 0,000323 | ||
| 21 шаг | 0,321493 | -0,00264 | 10,88214 | 0,321736 | 0,000242 | ||
| 22 шаг | 0,321736 | -0,00197 | 10,86921 | 0,321917 | 0,000181 | ||
| 23 шаг | 0,321917 | -0,00147 | 10,85956 | 0,322053 | 0,000136 | ||
| 24 шаг | 0,322053 | -0,0011 | 10,85235 | 0,322154 | 0,000101 | ||
| 25 шаг | 0,322154 | -0,00082 | 10,84696 | 0,32223 | 7,58E-05 | ||
| 26 шаг | 0,32223 | -0,00061 | 10,84294 | 0,322287 | 5,66E-05 |
Мы видим, что метод касательных долго приближает нас к искомому корню. X=0,3222
Литература
1. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966
|
|
|
3. Калиткин Н.Н. Численные методы. М.: Наука, 1978
4. Марчук Г.И. Методы вычислительной математики. М.: Наука, 1989.
5. Моисеев В.С., Горбунов Д.А. Метод малого параметра для решения задач анализа и синтеза проектных решений на базе неявно заданных функциональных зависимостей. //Изв.вузов, Авиационная техника, 1998, №4, с.3-10
6. Иванов В.С., Ляшев А.С. Лабораторный практикум по дисциплине «Вычислительная техника в инженерных и экономических расчетах». Казань, КАИ, 1984.
7. Вахонина Г.С. Методическое руководство к выполнению лабораторных работ по дисциплине “Методы вычислений”. – Казань: КАИ, 1982.
8. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
Дата добавления: 2021-12-10; просмотров: 335; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!