Пример решения пары двойственных задач

Используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи:

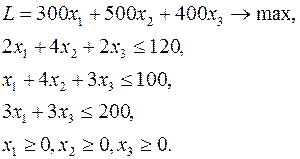(20)

Пусть решение задачи найдено одним из стандартных методов: 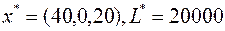. Построим двойственную задачу:

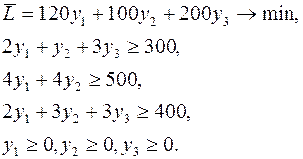(21)

По первой теореме двойственности задача разрешима, причем 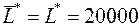. Найдем оптимальный план 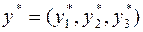задачи (21), используя вторую теорему двойственности. Подставим координаты вектора 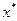в ограничения задачи (20). Получим

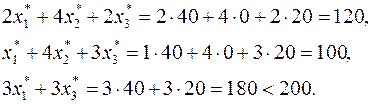
Следовательно, в силу УДН, неравенство 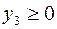должно выполняться как равенство, т.е. 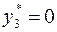. Далее так как 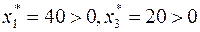, то в силу УДН

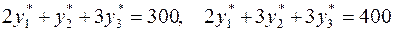Получаем систему линейных уравнений и решаем ее:

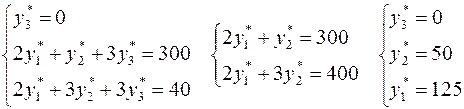Планы 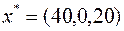и 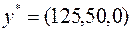удовлетворяют УДН, следовательно, в силу второй теоремы двойственности, являются оптимальными в задачах (20) и (21) соответственно.

Пример проверки вектора на оптимальность

Исследовать вектор 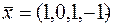на оптимальность в задаче ЛП:

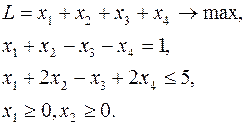
Вначале нужно проверить, является ли вектор 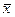допустимым. Для этого подставляем координаты вектора в ограничения:

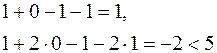Так как второе ограничение выполняется как строгое неравенство, то в силу УДН для оптимальности вектора 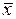необходимо выполнение равенства .

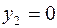Построим двойственную задачу:

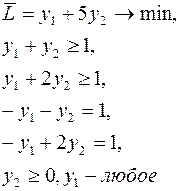Поскольку 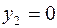, то из третьего и четвертого ограничений получаем 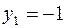. Но по УДН из условия 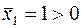следует, что должно выполняться равенство в первом ограничении двойственной задачи:

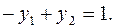
Подставляя значения 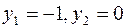, получим 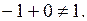Следовательно, УДН не выполняются и вектор 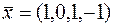не является оптимальным в исходной задаче.

Метод Гомори

Постановка задачи ЦЛП

Задача целочисленного программирования (ЦЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами:

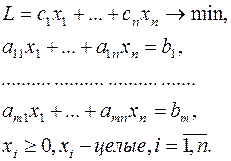(22)

Симплекс-метод не гарантирует целочисленности решения задачи (22), поэтому для отыскания оптимального целочисленного решения задачи ЦЛП требуются специальные методы. Один из таких методов, приводящий к целочисленному решению за конечное число шагов, предложен американским математиком Р. Гомори [1,2]. Идея метода следующая.

С помощью симплекс-метода решается задача ЛП без условия целочисленности. Если оптимальное решение получается нецелочисленным, то вводится дополнительное ограничение, которое, уменьшая многогранник допустимых решений (отсекая некоторую его часть), не исключает из него целочисленных точек. Если оптимальное решение задачи ЛП с дополнительным ограничением целочисленное, то вычисления заканчивают; если же оптимальное решение содержит хотя бы одну дробную компоненту, добавляют новое дополнительное ограничение.

Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо не будет найдено целочисленное оптимальное решение, либо показано, что задача не имеет целочисленных решений.

Алгоритм метода Гомори

Шаг 1. Симплекс-методом находим оптимальное решение задачи (22) без учета условия целочисленности. Если задача не имеет решения, то неразрешима и исходная задача ЦЛП. В этом случае алгоритм завершает работу.

Шаг 2. Пусть оптимальная таблица имеет вид:

	b		…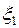
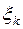
L			…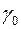
			…
…	…	…………..
			…

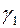
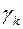
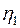
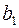
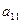
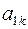
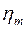
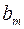
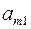
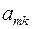
Если элементы 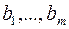– целочисленные, то оптимальное решение 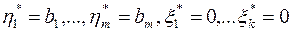является целочисленным. В этом случае вычисления заканчиваем. Иначе, переходим к следующему шагу.

Шаг 3. Среди дробных компонент 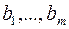таблицы выбираем элемент 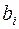с максимальной дробной частью 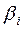и по строке i составляем дополнительное ограничение:

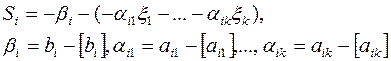Здесь 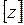– целая часть числа 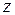(наибольшее целое число, не превышающее число ).

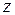Шаг 4. Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.

Замечания

Признаком отсутствия целочисленного решения служит появление в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами (поскольку соответствующее уравнение неразрешимо в целых числах).

На шаге 4 двойственный симплекс-метод применяется до тех пор, пока не будет получена оптимальная симплексная таблица (возможно, потребуется несколько итераций).

Если на шаге 4 в базис вводится переменная дополнительного ограничения 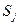, то эта строка вычеркивается из симплексной таблицы (соответствующее ограничение является избыточным).

Пример решения задачи ЦЛП

Решить задачу ЦЛП:

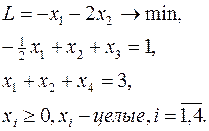
Решаем задачу без условия целочисленности симплекс-методом. Оптимальная таблица имеет вид

	b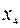
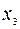
L	-14/3	-4/3	-2/3
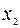
	5/3	1/3	2/3
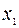
	4/3	2/3	-2/3

Оптимальное решение 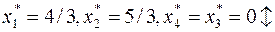не является целочисленным. Выберем среди нецелочисленных переменных 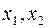переменную 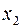с максимальной дробной частью и построим соответствующее отсечение:

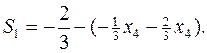
Приписывая это ограничение к симплексной таблице, и проводя стандартное преобразование двойственным симплекс-методом, получим:

	b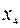
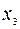
L	-14/3	-4/3	-2/3
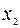
	5/3	1/3	2/3
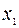
	4/3	2/3	-2/3
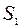
	-2/3	-1/3	-2/3

	b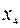
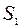
L	-4	-1	-1
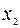
	1	0	1
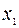
	2	1	-1
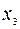
	1	1/2	-3/2

Полученная таблица является оптимальной. Соответствующее оптимальное решение 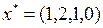является целочисленным. Значение функции на этом решении .

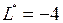Транспортная задача ЛП

Постановка задачи

Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта. Заданы величины:

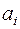- объем производства (запас) i-го поставщика, ;

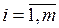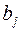- объем потребления (спрос) j-го потребителя,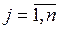

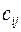- стоимость перевозки (транспортные затраты) единицы продукции от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен, и при этом общая стоимость всех перевозок была бы минимальна [1,3].

Транспортная задача, в которой суммарные запасы 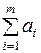и суммарные потребности 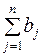совпадают, называется закрытой моделью; в противном случае – открытой. Открытая модель решается приведением к закрытой модели.

Математическая закрытая модель транспортной задачи имеет вид

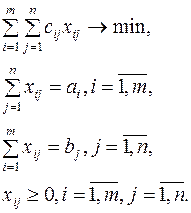
В случае, когда суммарные запасы превышают суммарные потребности, то есть 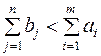, вводится фиктивный n+1 потребитель, потребности которого .

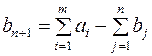В случае, когда суммарные потребности превышают суммарные запасы, то есть 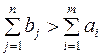, вводится фиктивный m+1 поставщик, запасы которого .

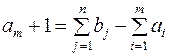Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.

Прежде чем решать транспортную задачу, необходимо проверить, к какой модели она принадлежит, и если необходимо, то привести ее к закрытой модели.

5.2. Построение опорного плана транспортной задачи

Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид:

	1	…	n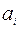
1		…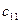
…	…	…	…	…
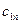
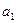
m		…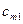
		…		=

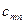
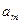
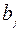
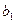
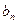
Базисными клетками транспортной таблицы являются клетки с отличными от нуля положительными перевозками, остальные клетки – свободные. Базисные клетки образуют опорный план транспортной задачи, еcли выполняются два условия:

сумма перевозок в каждой строке равна запасу 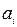в данной строке;

сумма перевозок в каждом столбце равна соответствующему спросу .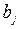

Опорный план транспортной задачи содержит не более 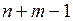отличных от нуля перевозок .

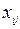Опорный план называется вырожденным, если число ненулевых перевозок 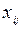меньше 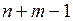, опорный план – невырожденный, если число ненулевых перевозок равно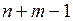

Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях [1,3].

Метод северо-западного угла

Рассмотрим «северо-западный угол» незаполненной таблицы, то есть клетку, соответствующую первому поставщику и первому потребителю.

Возможны три случая:

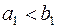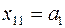Если , то . Это означает, что первый поставщик отгрузил весь продукт первому потребителю и его запас равен нулю, поэтому 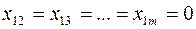. При этом неудовлетворенный спрос в первом пункте потребления равен .

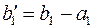Если 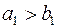, то 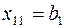, то есть спрос первого потребителя полностью удовлетворен и поэтому 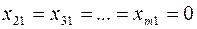, а остаток продукта в первом пункте производства равен .

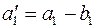В случае 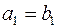из рассмотрения можно исключить и поставщика и потребителя. Однако при этом план получается вырожденным, поэтому считается, что выбывает только поставщик, а спрос потребителя остается неудовлетворенным и равным нулю.

После этого рассматриваем северо-западный угол оставшейся незаполненной части таблицы и повторяем те же действия. В результате через 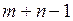шагов получим опорный план.

5.4. Пример построения опорного плана методом северо-западного угла

Найти опорный план транспортной задачи:

	1	2	3
1	15	20		35	20	0	0
2		0	30	30	30	30
	15	20	30	=
	0	20	30
	0	0	30
	0	0	0

В таблице, обведенной снизу и справа двойной чертой, указаны объемы перевозок, полученные методом северо-западного угла. При этом небазисные нулевые перевозки не проставлены. Справа и внизу таблицы содержатся объемы возможных запасов и спросов. В число базисных перевозок вошла перевозка 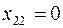, так как на предыдущем шаге 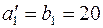и по п.3 метода считается выбывшим только поставщик, а неудовлетворенный спрос второго потребителя равен .

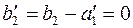Метод минимальной стоимости

Отличается от метода северо-западного угла только тем, что вместо «северо-западного» угла незаполненной таблицы выбирается клетка с минимальной стоимостью.

5.6. Пример построения опорного плана методом минимальной стоимости

Опорный план, построенный по методу минимальной стоимости.

	1	2	3
1	⁹	5⁷	30¹	35	5	5	5
2	15²	15³	⁸	30	30	15	0
	15	20	30	=
	15	20	0
	0	20	0
	0	5	0

Метод потенциалов

Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке цикла совершает поворот на 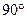. Знаком «+» отмечают те вершины, в которых перевозки увеличиваются, а знаком «-» - те вершины цикла, в которых перевозки уменьшаются. Перемещение какого-то количества единиц груза по циклу означает увеличение перевозок на это количество единиц в положительных вершинах и уменьшение в отрицательных вершинах. При этом, если перевозки остаются неотрицательными, план остается допустимым, а стоимость плана может меняться.

Ценой цикла называется изменение стоимости перевозок при перемещении единицы груза по этому циклу. Очевидно, цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, при этом стоимости в положительных вершинах берутся со знаком «+», а в отрицательных со знаком «-».

Идея метода потенциалов состоит в следующем [1,3]. Для любой свободной клетки транспортной таблицы всегда существует единственный цикл, положительная вершина которого лежит в этой свободной клетке, а все остальные – в базисных. Если цена такого цикла отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить больше единиц груза, возникнут отрицательные перевозки). Если циклов с отрицательной ценой нет, то это означает, что дальнейшее улучшение плана невозможно, то есть оптимальный план найден.

Для нахождения циклов с отрицательной ценой вводится система платежей 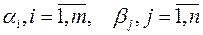и определяются величины 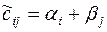, называемые «псевдостоимостями» перевозок единицы груза из пункта i в пункт j. При этом цена цикла пересчета для каждой свободной клетки равна 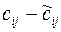, если платежи 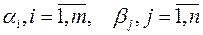, определять из условия

для всех базисных клеток (i,j).

Дата добавления: 2021-12-10; просмотров: 27; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Мы поможем в написании ваших работ!