Другие алгоритмически неразрешимые задачи
Прошу Вас в срок до (21.04.20) ознакомиться с информацией и выполнить практическое задание по данной теме.
Готовые задания присылать на электронную почту:
(gp.konnova@mail.ru) либо ВКОНТАКТЕ
Тема: Тьюрингов подход к понятию «алгоритм». Алгоритмически разрешимые и неразрешимые проблемы
В теории алгоритмов используются различные подходы к формализации понятий алгоритма и вычислимой функции. Поиск таких подходов проходил в трех направлениях. В первом всякий алгоритм вычисляет значение некоторой числовой функции, а его элементарные шаги — это арифметические операции. Последовательность шагов определяется с помощью суперпозиции — подстановки функций в функции, рекурсии — определения значения функции через ранее вычисленные значения этой же функции, и оператора минимизации, благодаря которому из всюду определенной функции можно получить не всюду определенную вычислимую функцию. Класс функций, порождаемый этими тремя операторами, называется классом частично-рекурсивных функций. Второе направление основано на определении алгоритмического процесса как процесса, осуществимого на конкретной теоретической машине. Примерами таких алгоритмических моделей являются “машина Тьюринга” и “машина Поста”. Третье направление отвлекается от конкретных машин (т.е. в этих моделях отсутствуют понятия “память”, “состояние машины” и т.п.). Наиболее известная алгоритмическая модель этого типа — нормальные алгоритмы Маркова.
|
|
|
Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.
Клетка (qj, ai) определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание: какой символ записать в текущую ячейку, куда передвинуть головку чтения/записи, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: “Л” (влево), “П” (вправо) или “Н” (неподвижен).
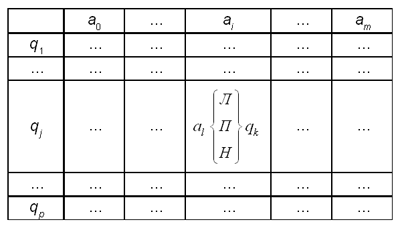
После выполнения очередной команды МТ переходит в состояние qk (которое может в частном случае совпадать с прежним состоянием qj). Следующую команду нужно искать в k-й строке таблицы на пересечении со столбцом, соответствующим букве, которую автомат видит после сдвига. В процессе работы автомат перескакивает из одной клетки программы, записанной в виде таблицы, в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q0, т.е. остановиться. Будем говорить, что такие клетки содержат команду останова.
Если клеток останова в программе вообще нет или в процессе работы над входным словом МТ никогда не окажется в заключительном состоянии, то считается, что машина Тьюринга неприменима к данному входному слову. Машина Тьюринга применима к входному слову только в том случае, если, начав работу над этим входным словом, она окажется в заключительном состоянии.
|
|
|
Пример. Пусть требуется построить машину Тьюринга, которая прибавляет единицу к числу на ленте. Входное слово состоит из цифр целого десятичного числа, записанных в последовательные ячейки на ленте. В начальный момент машина находится против самой правой цифры числа.
Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее заменить на 0 и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:
Тезис Тьюринга состоит в том, что всякий алгоритм может быть реализован соответствующей машиной Тьюринга. Тезис Тьюринга является основной нематематической гипотезой теории алгоритмов, понимаемых по Тьюрингу. Одновременно этот тезис приводит к формальному определению алгоритма.
Алгоритм (по Тьюрингу) — программа для машины Тьюринга, приводящая к решению поставленной задачи.
Математики в течение веков пользовались интуитивным понятием алгоритма (см. “Алгоритм”). В рамках подобного определения были сформулированы и успешно применялись на практике алгоритмы для решения таких задач, как выполнение арифметических действий “столбиком”, нахождение корней квадратных уравнений, решение систем линейных уравнений и т.д. Постепенно они переходили к постановке и решению все более сложных задач. Так, Г.Лейбниц в XVII веке пытался построить общий алгоритм решения любых математических задач. В XX веке эта идея приобрела более конкретную форму: построить алгоритм проверки правильности любой теоремы при любой системе аксиом. Построить такие алгоритмы не удавалось, и математики выдвинули предположение: а вдруг для того или иного класса задач в принципе невозможно построить алгоритм решения? На основе этого предположения возникло понятие алгоритмически неразрешимой задачи — задачи, для которой невозможно построить процедуру решения.
|
|
|
Проблема останова
Одной из первых проблем, для которых была строго доказана алгоритмическая неразрешимость, была так называемая проблема останова. Сформулируем ее для программ, написанных на процедурных языках программирования (см. “Языки программирования”).
|
|
|
Зададимся следующим вопросом. Нельзя ли определить программным способом, с помощью самого компьютера, зациклится ли данная программа на определенных входных данных? Может быть, можно написать некоторую универсальную программу (обозначим ее через U), которая принимала бы на вход текст заданной программы и входные данные к ней, анализировала его и выдавала бы ответ, зациклится эта программа на этих входных данных или нет1. Возможность написания программы U кажется правдоподобной: ведь, например, программа-компилятор умеет анализировать текст заданной программы на наличие в нем возможных синтаксических ошибок и т.п. Программа U могла бы стать надстройкой над компилятором, которая вылавливала бы ошибку особого рода — ошибку “бесконечного цикла”.
Уточним формулировку задачи. Каждая программа П в каждом конкретном случае работает с входными данными. (Строго говоря, некоторые программы, например программа вычисления числа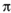 
с точностью до 100 000 знаков, могут и ничего не получать на вход — в этом случае будем считать, что входные данные для такой программы образуют “пустой набор” — файл из нуля байт.) Можно считать, что эти входные данные берутся всегда из какого-то файла Д. Действительно, все входные данные — символы, вводимые с клавиатуры, файлы и даже движения мышки (здесь подразумевается, что нажатие определенных кнопок в интерфейсе программы — это тоже ввод данных в нее) — можно закодировать в одном общем файле данных. Может случиться, что некоторая программа, получая на вход одни данные, зацикливается, а получая другие — нет.
Работу программы U можно спроектировать следующим образом. Программа U должна получать на вход, во-первых, текст программы П (текстовый файл), а во-вторых, некоторый файл с данными Д (текстовый файл). Затем она должна проанализировать эти два файла и выдать точный ответ: зациклится ли программа П, если П получила на вход файл Д. Можно всегда считать, что программа U может воспринимать на вход любые файлы: например, если файл П не является синтаксически правильной программой на выбранном языке программирования (скажем, Паскале), то программа U это легко определяет, но все равно считает, что в этом случае П является “программой”: например, такой, которая “ничего не делает” и, следовательно, не зацикливается. Соответственно, если файл Д имеет “неправильный формат” (например, на вход программе П требуется число, а в файле Д имеется что-то другое), то программа П всегда останавливается на этих “неправильных данных”. Итак, вот более точное описание программы U:
а) программа U читает два произвольных файла: П и Д;
б) если файл П содержит синтаксически правильную программу (для определенности, на Паскале), а файл Д представляет собой корректные данные для программы П, то программа U проверяет, зациклится ли П на данных Д. Если она зациклится, то на экран компьютера будет выдано сообщение “зациклится”, иначе — “не зациклится”;
в) если файлы П и Д не удовлетворяют условиям б), то на экран выдается сообщение “не зациклится” (и в этой ситуации для простоты мы все равно называем П программой, а Д — данными, и П в этом случае не зацикливается на Д “по определению”).
Предположим, что нам удалось написать такую программу U. Можно считать, что она тоже написана на Паскале. Теперь мы собираемся написать новую программу, которую обозначим через U1. Но прежде мы введем специальное понятие — стандартный номер файла. Любой файл можно представить как слово, быть может, очень длинное. Каждая “буква” этого слова берется из некоторого алфавита. Например, можно считать, что алфавит для таких слов состоит из 256 символов, а каждая буква в слове — это один байт в файле; в качестве “букв” здесь выступают все ASCII-символы — “настоящие буквы”, знаки препинания, пробел, специальные символы и т.д. Таким образом, все файлы могут быть расположены в некоторую упорядоченную бесконечную последовательность:
Ф0, Ф1, Ф2, Ф3, ... (*)
(Сначала идет пустой файл Ф0, в котором нет ни одного байта. Затем перечисляются в алфавитном порядке все файлы, состоящие из одной “буквы”, затем — состоящие из двух “букв”, и т.д.) В этой последовательности каждый файл получает некоторый номер. Этот номер мы и назовем стандартным номером файла. Ясно, что можно написать программу, которая по заданному файлу вычислит стандартный номер этого файла. (Мы считаем, что у нас есть “идеальный” компьютер. Он не имеет ограничений памяти и поэтому может работать с числами, состоящими из сколь угодно большого количества цифр.) Можно также написать программу, которая по заданному числу восстанавливает файл, стандартный номер которого равен n.
Итак, любой файл попадает в последовательность (*) и имеет в ней свой уникальный номер, который мы называем стандартным номером этого файла. Значит, и у любого файла с программой (П), и у любого файла данных (Д) есть свои стандартные номера.
Теперь можно написать программу U1, которая будет делать следующее:
1) получать на вход натуральное число i;
2) восстанавливать файл Фi из последовательности (*), т.е. восстанавливать файл со стандартным номером i;
3) запускать программу U, подавая ей на вход в качестве файла П файл Фi, а в качестве файла Д — тот же самый файл Фi.
Коротко работу программы U1 можно описать так: по заданному числу i она определяет, зациклится ли программа, реализованная в файле со стандартным номером i при работе с данными, записанными в файле, который имеет стандартный номер i (эта программа решает проблему самоприменимости).
Ясно, что программу U1 всегда можно написать так, чтобы она в самом конце работы некоторой переменной z присваивала значение 0 или 1, и в соответствии с этим значением выводила одно из двух сообщений:
if z = 0 then writeln('нe зациклится')
else writein('зациклится')
Теперь подвергнем программу U1 маленькой переделке. Фрагмент, приведенный выше, заменим на такой (**):
if z = 0 then
Repeat
until 1 = 2
else writeln('зациклится')
Эту программу (назовем ее U2) сохраним в другом файле. Что делает U2? Она тоже, как и U1, получает на вход число i, но отличается от U1 вот чем: если выяснилось, что исследуемая программа со стандартным номером i не зацикливается на файле данных со стандартным номером i, то сама U2 зацикливается, а в противном случае U2 выдает сообщение “зациклится” и после этого завершает работу.
Программа U2 сама тоже записана в файле. Этот файл обязательно находится в последовательности (*) и имеет некоторый стандартный номер. Пусть k — этот номер. Здесь начинается самое интересное. Что произойдет, если на вход программе U2 в качестве числа i мы подадим число k? В этом случае, конечно, выполнение программы U2 может либо зациклиться, либо остановиться. Предположим, что оно остановится. Тогда, как только компьютер дойдет до выполнения фрагмента (**), переменная z должна получить нулевое значение. После этого, в соответствии с (**), произойдет зацикливание. Предположив, что выполнение остановится, мы выяснили, что выполнение зациклится! Это невозможно. Теперь предположим, что выполнение зациклится. Но тогда программа U2, как говорилось выше, должна выдать сообщение “зациклится” и после этого остановиться. Это тоже невозможно.
Таким образом, программа должна зациклиться, если она остановится, и должна остановиться, если она зациклится. В чем тут дело? Конечно же в том, что мы предполагали возможность написания универсальной программы U, которая определяла бы любую программу на возможность зацикливания. Итак, такой программы U не существует в принципе, или, как говорят математики, проблема останова алгоритмически неразрешима.
Неразрешимость проблемы останова впервые была доказана Аланом Тьюрингом в его работе, опубликованной в 1936 г. Конечно, тогда не было никаких компьютеров и тем более языков программирования, да и сам Тьюринг в той работе даже не пользовался термином “программа”. Но его изложение, по сути, мало чем отличалось от нашего. Мы использовали язык Pascal и говорили о привычных нам компьютерах, однако ясно, что эти подробности (о файлах, о конкретном языке программирования) были совсем не важны: существо наших рассуждений было чисто логическим.
Другие алгоритмически неразрешимые задачи
Упомянутая в начале статьи проблема проверки правильности любых математических утверждений также оказалась алгоритмически неразрешимой. Сформулируем ее формально в более общем виде.
Пусть у нас есть посылка R и следствие S, записанные в виде слов (формул) в некотором алфавите, состоящем из букв, цифр, скобок, знаков математических и логических операций. Процесс вывода следствия S из посылки R может быть описан путем указания последовательности допустимых формальных преобразований слов (дедуктивной цепочки).
Проблему распознавания выводимости можно сформулировать следующим образом: Существует ли для любых двух слов R и S дедуктивная цепочка, ведущая от R к S? Решение понимается в смысле существования алгоритма, дающего ответ на этот вопрос для любых слов R и S. В 1936 г. американский математик Черч доказал теорему о том, что проблема распознавания выводимости алгоритмически неразрешима. Тем самым выяснилась причина безуспешности всех прошлых попыток решения задачи, поставленной Лейбницем.
Неразрешимой оказалась и так называемая “10-я проблема Гильберта”. В упрощенной формулировке она звучит так: требуется выработать алгоритм, позволяющий для любого алгебраического уравнения P(x1, x2, …, xn) = 0, где P — многочлен с целыми коэффициентами, выяснить, имеет ли оно целочисленное решение. В 1970 г. советский математик Ю.В. Матиясевич доказал невозможность построения алгоритма для решения этой задачи. Интересно, что если для конкретного уравнения известно, что решение в целых числах есть, то алгоритм отыскания этого решения существует.
Какие методы используются для доказательства алгоритмической неразрешимости? Обычно неразрешимость новых задач доказывается методом сведения к этим задачам известных алгоритмически неразрешимых задач. Тем самым доказывается, что если бы была разрешима новая задача, то можно было бы решить и заведомо неразрешимую задачу. Применяя метод сведения, обычно ссылаются на искусственные задачи, которые не представляют самостоятельного интереса, но для которых легко непосредственно доказать их неразрешимость, например, описанную выше проблему самоприменимости.
Методические рекомендации
Данная тема включена в стандарт профильного курса информатики в следующей формулировке: диагональное доказательство несуществования. Здесь имеется в виду канторовский диагональный процесс, который можно использовать для доказательства алгоритмической неразрешимости, в частности, проблемы останова. Именно поэтому в качестве основного материала статьи приведено такое доказательство этой проблемы, которое легко сводится к рассуждениям Кантора. Следует лишь описать канторовские массив-таблицу Т и массив-строку D.
В проблеме останова T[i,j] — крестик, если программа, реализованная в файле со стандартным номером i, зацикливается на данных, расположенных в файле со стандартным номером j, иначе — нолик. Значения T[i,j] для любых заданных i и j могла бы вычислять, после небольших модификаций, программа U (если бы, конечно, она существовала). Значение D[i] — нолик, если программа, реализованная в файле со стандартным номером i, зацикливается на данных, расположенных в файле со стандартным номером i, иначе — крестик. Значения D[i] можно было бы вычислять, используя программу U1. Тогда D[i] не равно Т[i,i] для всех индексов i и D не совпадает ни с одной строкой таблицы Т. А если бы программа U1 существовала, то она имела бы свой номер и ей соответствовала бы одна из строк таблицы T.
Подробнее о канторовском диагональном процессе и соответствующем доказательстве проблемы останова можно прочитать в уже упомянутой статье И.Долмачева “Алан Тьюринг”, которую также можно найти на сайте газеты “Информатика” (в архивных материалах № 5/2000). Два других доказательства алгоритмической неразрешимости данной проблемы можно прочитать в учебнике Е.В. Андреевой, Л.Л. Босовой, И.Н. Фалиной “Математические основы информатики” (М.: БИНОМ. Лаборатория Знаний, 2005) и в методическом пособии к этому учебнику (М.: БИНОМ. Лаборатория Знаний, 2006). Выбор доказательства остается на усмотрение учителя. Например, если в курс информатики включается рассмотрение машины Тьюринга, то и доказательство алгоритмической неразрешимости можно проводить с использованием этого формального аппарата.
Тем не менее сама тема имеет очень важное, в том числе культурологическое, значение, и в профильной школе должна быть рассмотрена обязательно, а в основной — по крайней мере должен быть сформулирован сам факт существования алгоритмически неразрешимых задач. Ведь сам по себе этот факт является весьма неочевидным, о чем говорят и многовековые попытки решить те или иные проблемы (задача доказать их возможную алгоритмическую неразрешимость при этом изначально даже не ставилась). Ученики также воспринимают данный факт с недоверием, причем даже после доказательства неразрешимости, например, проблемы останова. Ведь их практический опыт подсказывает, что очень часто они сами могут эту проблему для конкретной программы решить, в том числе и доказать, что определенная программа на конкретных входных данных зациклится. Здесь очень важно провести грань между решением задачи для частного случая и построением универсального алгоритма. Действительно, проблему останова для конкретной программы или даже класса программ решить можно. Так, для программы, состоящей только из линейных конструкций, легко показать, что она всегда закончит свою работу. Приведенное же доказательство говорит о невозможности построения общего алгоритма, пригодного для любых программ и входных данных.
Особо следует отметить, что не решает данную проблему и компьютерный запуск программы на конкретных входных данных (такой способ часто предлагают сами школьники). В самом деле, если программа закончила свою работу, то мы можем сказать, что она не зацикливается. Однако если окончания работы программы мы не дождались, то это не означает ничего: программа может как зациклиться, так и просто долго работать.
Главная цель формализации понятия алгоритма такова: подойти к решению проблемы алгоритмической разрешимости различных математических задач, т.е. ответить на вопрос, может ли быть построен алгоритм, приводящий к решению задачи. Мы рассмотрим постановку этой проблемы и некоторые результаты теории алгоритмической разрешимости задач, но вначале обсудим формализацию понятия алгоритма в теории автоматов на примере машин Поста, Тьюринга, а также нормальных алгоритмов Маркова, а затем - основы теории рекурсивных функций. Идеи λ-исчислений Черча реализованы в языке программирования LISP (глава 3).
Вместе с тем, формально определенный любым из известных способов алгоритм не может в практическом программировании заменить то, что мы называли алгоритмами в предыдущем параграфе. Основная причина состоит в том, что формальное определение резко сужает круг рассматриваемых задач, делая многие практически важные задачи недоступными для рассмотрения.
МАШИНА ПОСТА
Абстрактные (т.е. существующие не реально, а лишь в воображении) машины Поста и Тьюринга, предназначенные для доказательств различных утверждений о свойствах программ для них, были предложены независимо друг от друга (и практически одновременно) в 1936 г. американским математиком Эмилем Постом и английским математиком Алланом Тьюрингом. Эти машины представляют собой универсальных исполнителей, являющихся полностью детерминированными, позволяющих «вводить» начальные данные, и после выполнения программ «читать» результат. Машина Поста менее популярна, хотя она значительно проще машины Тьюринга. С ее помощью можно вести обучение первым навыкам составления программ для ЭВМ.
Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V», и головки, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, или проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка («-») находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста, рис. 1.16.
Рис. 1.16. Абстрактная машина Поста
Команда машины Поста имеет следующую структуру:
п Km,
где п - порядковый номер команды, K-действие, выполняемое головкой, т - номер следующей команды, подлежащей выполнению.
Существует всего шесть команд машины Поста, рис. 1.17:
Рис. 1.17. Команды машины Поста
Ситуации, в которых головка должна наносить метку там, где она уже имеется, или, наоборот, стирать метку там, где ее нет, являются аварийными (недопустимыми).
Программой для машины Поста будем называть непустой список команд, такой что 1) на п-м месте команда с номером n; 2) номер т каждой команды совпадает с номером какой-либо команды списка.
С точки зрения свойств алгоритмов, изучаемых с помощью машины Поста, наибольший интерес представляют причины останова машины при выполнении программы:
1) останов по команде «стоп»; такой останов называется результативным и указывает на корректность алгоритма (программы);
2) останов при выполнении недопустимой команды; в этом случае останов называется безрезультативным;
3) машина не останавливается никогда; в этом и в предыдущем случае мы имеем дело с некорректным алгоритмом (программой).
Будем понимать под начальным состояние головки против пустой клетки левее самой левой метки на ленте.
Рассмотрим реализацию некоторых типичных элементов программ машины Поста.
1. Пусть задано исходное состояние головки и требуется на пустой ленте написать две метки: одну в секцию под головкой, вторую справа от нее. Это можно сделать по следующей программе (справа от команды показан результат ее выполнения):
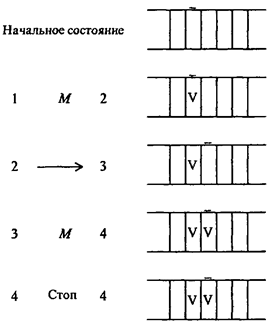
Рис. 1.18. Пример элемента программы машины Поста
2. Покажем, как можно воспользоваться командой условного перехода для организации циклического процесса. Пусть на ленте имеется запись из нескольких меток подряд и головка находится над самой крайней меткой справа. Требуется перевести головку влево до первой пустой позиции.
Программа будет иметь следующий вид:
Команда условного перехода является одним из основных средств организации циклических процессов, например, для нахождения первой метки справа (или слева) от головки, расположенной над пустой клеткой; нахождение слева (или справа) от головки пустой клетки, если она расположена над меткой и т.д.
3. Остановимся на представлении чисел на ленте машины Поста и выполнении операций над ними.
Число k представляется на ленте машины Поста идущими подряд k + 1 метками (одна метка означает число «О»). Между двумя числами делается интервал как минимум из одной пустой секции на ленте. Например, запись чисел 3 и 5 на ленте машины Поста будет выглядеть так:
Обратим внимание, что используемая в машине Поста система записи чисел является непозиционной.
Составим программу для прибавления к произвольному числу единицы. Предположим, что на ленте записано только одно число и головка находится над одной из клеток, в которой находится метка, принадлежащая этому числу:
Для решения задачи можно переместить головку влево (или вправо) до первой пустой клетки, а затем нанести метку.
Программа, добавляющая к числу метку слева, имеет вид:
Программа, добавляющая к числу метку справа, имеет вид:
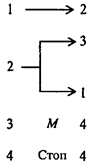
(отличие только в направлении движения головки в первой команде. Проверьте работоспособность этих программ на каких-либо частных примерах).
Предположим, что головка расположена на расстоянии нескольких клеток слева от числа, к которому нужно прибавить единицу. В этом случае программа усложняется. Появится «блок поиска числа» - две команды, приводящие головку в состояние, рассмотренное в предыдущем примере:
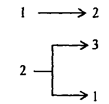
Ниже - полные тексты программ, добавляющие единицу слева и справа, соответственно:
В первом случае не нужно перемещать головку к крайней левой метке числа
4. Приведем программу для сложения целых неотрицательных чисел а и и на машине Поста, когда головка находится над числом а, а число b находится правее числа а на некоторое число клеток. Эта программа реализует следующий алгоритм: первое число постепенно придвигается ко второму до их слияния, а потом стирается одна метка (иначе результат оказался бы на единицу больше правильного).
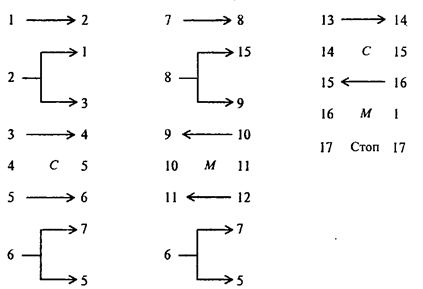
В случае более сложных начальных условий, когда неизвестно, справа или слева от головки (и на какое число клеток) находится число, можно применить такой принцип поиска числа: двигая головку вправо и влево и отмечая метками степень удаления головки от исходного положения, найти число, а потом уже применить известную программу сложения. При этом проверяется, находится ли головка над одной из меток числа и если да, то задача решена. Иначе проверяется, пуста ли секция справа от головки и следующая за ней; если обе пусты, то делается возврат головки на один шаг и ставится метка, а затем такая же операция выполняется слева и по отмеченной дорожке головка возвращается вправо и т.д. до тех пор, пока головка не натолкнется на число, после чего можно применить ранее рассмотренные выше программы:
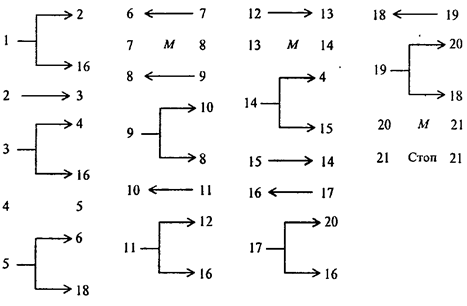
Машину Поста можно рассматривать как упрощенную модель ЭВМ. В самом деле, как ЭВМ, так и машина Поста имеют:
• неделимые носители информации (клетки - биты), которые могут быть заполненными или незаполненными;
• ограниченный набор элементарных действий - команд, каждая из которых
выполняется за один такт (шаг).
Обе машины работают на основе программы. Однако, в машине Поста информация располагается линейно и читается подряд, а в ЭВМ можно читать информацию по адресу; набор команд ЭВМ значительно шире и выразительнее, чем команды машины Поста и т.д.
МАШИНА ТЬЮРИНГА
Машина Тьюринга подобна машине Поста, но функционирует несколько иначе.
Машина Тьюринга (МТ) состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний qo, q1, ..., qs, принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний). При этом qо называется начальным состоянием.
Читающая и пишущая головка может читать буквы рабочего алфавита А = [а0, a1, ..., аt}, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква a0 - «пробел». Головка находится в каждый момент времени над некоторой ячейкой ленты -текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты. При этом возможна ситуация выхода за левый край ленты (ЛК), которая является аварийной (недопустимой), или машинного останова (МО), когда машина выполняет предписание об остановке.
Порядок работы МТ (с рабочим алфавитом a0,a1,..., аt и состояниями q0, q1,..., qs) описывается таблицей машины Тьюринга. Эта таблица является матрицей с четырьмя столбцами и (s + 1) (t + 1) строками. Каждая строка имеет вид
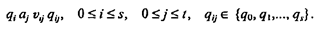
Здесь через vij обозначен элемент объединения алфавита {а0, а1,..., аt} и множества предписаний для лентопротяжного механизма: l - переместить ленту влево, r -переместить ленту вправо, s - остановить машину; vij - действие МТ, состоящее либо в занесении в ячейку ленты символа алфавита a0, а1, ..., аt, либо в движении головки, либо в останове машины; qij является последующим состоянием.
МТ работает согласно следующим правилам: если МТ находится в состоянии qi, головка прочитывает символ 0 в рабочей ячейке. Пусть строка qiаjvijqij, начинающаяся с символов qi, aj, встречается только один раз в таблице. Если vij - буква рабочего алфавита, то головка стирает содержимое рабочей ячейки и заносит туда эту букву. Если vij - команда r или l для лентопротяжного механизма, то лента сдвигается на одну ячейку вправо или влево (если не происходит выход за левый край ленты) соответственно. Если vij =s, то происходит машинный останов.
Машина Тьюринга начинает работу из некоторой начальной конфигурации, включающей в себя начальное состояние (обычно q0) и положение считывающе-записывающей головки над определенной ячейкой ленты, содержащей один из символов рабочего алфавита A.
Отметим, что наличие разнообразных символов в рабочем алфавите МТ позволяет представлять на ленте произвольную текстовую и числовую информацию, а переходы управляющего центра МТ в различные состояния моделируют запоминание машиной Тьюринга промежуточных результатов работы. Таблица, определяющая порядок работы МТ, не является в прямом смысле слова программой (ее предписания выполняются не последовательно, одно за другим, а описывают преобразования символов некоторого текста, находящегося на ленте). Таблицу МТ часто называют схемой машины Тьюринга или попросту отождествляют с самой машиной Тьюринга, коль скоро ее устройство и принцип функционирования известны.
Рассмотрим примеры нескольких схем машины Тьюринга.
1. Алгоритм прибавления единицы к числу п в десятичной системе счисления. Дана десятичная запись числа п (т.е. представление натурального числа п в десятичной системе счисления); требуется получить десятичную запись числа п + 1.
Очевидно, что внешний алфавит МТ должен состоять из десяти цифр 0,1,2,3,4,5,6,7,8,9 и символа пробела _. Эти цифры записывают по одной в ячейке (подряд, без пропусков).
Оказывается достаточным иметь два внутренних состояния машины: q1 и q2.
Предположим, что в начальный момент головка находится над одной из цифр числа, а машина находится в состоянии q1. Тогда задача может быть решена в два этапа: движения головки к цифре единиц числа (во внутреннем состоянии q1) и замене этой цифры на единицу большую (с учетом переноса 1 в следующий разряд, если это 9, во внутреннем состоянии q2. Соответствующая схема МТ может иметь вид
| аi | qi | |
| q1 | q2 | |
| 0 | 0Пq1 | 1Cq2 |
| 1 | 1Пq1 | 2Cq2 |
| 2 | 2Пq1 | 3Cq2 |
| 3 | 3Пq1 | 4Cq2 |
| 4 | 4Пq1 | 5Cq2 |
| 5 | 5Пq1 | 6Cq2 |
| 6 | 6Пq1 | 7Cq2 |
| 7 | 7Пq1 | 8Cq2 |
| 8 | 8Пq1 | 9Cq2 |
| 9 | 9Пq1 | 0Cq2 |
| - | -Лq1 | 1Cq2 |
2. Алгоритм записи числа в десятичной системе счисления.
Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Требуется записать в десятичной системе число этих меток пересчитать метки).
Суть алгоритма может состоять в том, что к числу 0, записанному на ленте в начале работы машины, машина добавляет 1, стирая метку за меткой, так что вместо нуля возникает число 0 + k.
Легко могут быть построены алгоритмы сложения чисел, их перемножения, нападения наибольшего общего делителя и т.д. Однако, главная цель введения машин Поста и Тьюринга не программирование для них, а изучение свойств алгоритмов и проблемы алгоритмической разрешимости задач.
В зависимости от числа используемых лент, их назначения и числа состояний устройства управления можно рассматривать различные модификации машин Тьюринга.
Предположим, мы расширили определение МТ, добавив определенное состояние q. устройства управления машины. Будем говорить, что если устройство управления переходит в состояние q0 для заданного входного слова х, то машина допускает х; если устройство переходит в состояние qx, то машина запрещает х. Такую машину будем называть машиной Тьюринга с двумя выходами. Могут быть рассмотрены многочисленные варианты машины Тьюринга, имеющие некоторое конечное число лент. В каждой клетке этих лент может находиться один из символов внешнего алфавита А = {a0, a1, ..., аn}. Устройство управления машиной в каждый момент времени находится в одном из конечного множества состояний Q = {q0, q1, ..., qm}. Для K-ленточной машины конфигурация ее в i-й момент времени описывается системой k-слов вида:
ail1 … aillqi aill+1 … si1t;
aik1 … aiklqi aikl+1 …aikv;
первый индекс соответствует моменту времени, второй - номеру ленты, третий -номеру клетки, считая слева направо. Говорят, что машина выполняет команду
qiaa1 … aak → qjab1k1 … abkkk,
К = {Л, С, П}.
Если, находясь в состоянии qi и обозревая ячейки с символами aa1 — aаk, машина переходит в состояние qj, заменяя содержимое ячеек соответственно символами аb1 — аbк, то после этого ленты соответственно сдвигаются в направлениях k1 ... kk.
До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм любой машины Тьюринга. Это достигается путем кодирования конфигурации и программы любой данной машины Тьюринга в символах внешнего алфавита универсальной машины. Само кодирование должно выполняться следующим образом:
1) различные символы должны заменяться различными кодовыми группами, но один и тот же символ должен заменяться всюду, где бы он не встретился, одной и той же кодовой группой;
2) строки кодовых записей должны однозначно разбиваться на отдельные кодовые группы;
3) должна иметься возможность распознать кодовые группы, соответствующие командам Л, П, С, различать кодовые группы, соответствующие символам внешнего алфавита и внутренним состояниям.
Для сравнения структур различных машин и оценки их сложности необходимо иметь соответствующую меру сложности машин. К.Шеннон предложил рассматривать в качестве такой меры произведение числа символов внешнего алфавита и числа внутренних состояний. Большой интерес вызывает задача построения универсальной машин Тьюринга наименьшей сложности.
Может быть рассмотрено еще одно обобщение машин Тьюринга: их композиции. Операции композиции, выполняемые над алгоритмами, позволяют образовывать новые, более сложные алгоритмы из ранее известных простых алгоритмов. Поскольку машина Тьюринга - алгоритм, то операции композиции применимы и к машинам Тьюринга. Рассмотрим основные из них: произведение, возведение в степень, итерацию.
Пусть заданы машины Тьюринга T1 и T2, имеющие общий внешний алфавит А = {a0, a1, ..., am} и внутренние состояния Q1 = {q0, q1,… qn} и Q2 = {q0, q1, ..., qt} соответственно. Композицией или произведением машины T1 и машины T2 будем называть машину Т с тем же внешним алфавитом А = {a0, а1, ...,am} и набором внутренних состояний Q = {q0, q1,..., q2,,qn+1,..., qn+1} и программой, эквивалентной последовательному выполнению программ машин Т1 и Т2:
Т =T1 * T2..
Таким же образом определяется операция возведения в степень: n-й степенью машины Т называется произведение T...Т c n сомножителями.
Операция итерации применима к одной машине и определяется следующим образом. Пусть машина T1 имеет несколько заключительных состояний. Выберем ее r-е заключительное состояние и отождествим его в схеме машины с ее начальным состоянием. Полученная машина Tявляется результатом итерации машины Т1 : Т = T1.
Прежде чем остановиться на проблеме алгоритмической разрешимости задач обратимся к другим способам формализации понятия алгоритма.
Практическое Задание:
Письменно ответить на контрольные вопросы и выполнить задания и прислать работу в указанный срок.
Контрольные вопросы и задания
1. Для чего необходимо формализовать понятие алгоритма?
2. Что означает фраза: «Машины Поста и Тьюринга являются абстрактными машинами»?
3. Для чего предназначены машины Поста и Тьюринга?
4. Как «устроена» машина Поста?
5. Перечислите и запишите команды машины Поста.
6. С помощью бумаги, карандаша и стиральной резинки «исполните» вместо машины Поста программы сложения чисел из текста.
7. Составьте (и проверьте) программу для машины Поста, создающую на ленте копию заданной последовательности меток справа от нее.
8. Пользуясь предыдущей программой, составьте программу умножения чисел для машины Поста.
9. Как «устроена» машина Тьюринга?
10. Каков принцип исполнения программы машиной Тьюринга?
11. Сравните машины Поста и Тьюринга. Укажите различия.
12. Выполните вместо машины Тьюринга примеры программ из текста.
Успехов при выполнении заданий!!!
Дата добавления: 2021-12-10; просмотров: 26; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!