Основное свойство направляющих косинусов
Правая и левая тройки векторов
Определение
Три некомпланарных вектора  ,
,  и
и 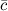 , приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
, приведенных к общему началу, образуют так называемую связку трех векторов (или тройку векторов).
Тройка векторов называется упорядоченной, если четко сказано, какой вектор в ней идет первым, и так далее.
Тройка векторов  ,
,  и
и 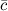 называется левой, если поворот от вектора
называется левой, если поворот от вектора  к вектору
к вектору  , видимый с конца третьего вектора
, видимый с конца третьего вектора 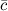 , осуществляется по ходу часовой стрелки (рис. 1).
, осуществляется по ходу часовой стрелки (рис. 1).
Тройка векторов  ,
,  и
и 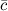 называется правой, если поворот от вектора
называется правой, если поворот от вектора  к вектору
к вектору  , видимый с конца третьего вектора
, видимый с конца третьего вектора 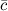 , осуществляется против хода часовой стрелки (рис. 2).
, осуществляется против хода часовой стрелки (рис. 2).

Координаты вектора. Направляющие косинусы
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Координаты вектора
Пусть задана прямоугольная декартова система координат (ПДСК) 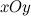 и произвольный вектор
и произвольный вектор  , начало которого совпадает с началом системы координат (рис. 1).
, начало которого совпадает с началом системы координат (рис. 1).

Определение
Координатами вектора  называются проекции
называются проекции 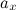 и
и  данного вектора на оси
данного вектора на оси  и
и  соответственно:
соответственно:

Величина 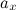 называется абсциссой вектора
называется абсциссой вектора  , а число
, а число  - егоординатой. То, что вектор
- егоординатой. То, что вектор  имеет координаты
имеет координаты 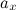 и
и  , записывается следующим образом:
, записывается следующим образом:  .
.
Пример
Запись  означает, что вектор
означает, что вектор  имеет следующие координаты: абсцисса равна 5, ордината равна -2.
имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Сумма двух векторов, заданных координатами
|
|
|
Пусть заданы  и
и  , тогда вектор
, тогда вектор  имеет координаты
имеет координаты  (рис. 2).
(рис. 2).

Определение
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
Пример
Задание. Заданы  и
и  . Найти координаты вектора
. Найти координаты вектора 
Решение. 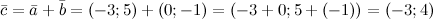
Умножение вектора на число
Если задан  , то тогда вектор
, то тогда вектор  имеет координаты
имеет координаты  , здесь
, здесь  - некоторое число (рис. 3).
- некоторое число (рис. 3).

Определение
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
Пример
Задание. Вектор 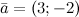 . Найти координаты вектора
. Найти координаты вектора 
Решение. 
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки  и
и  . Тогда координаты вектора
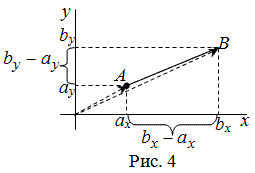
. Тогда координаты вектора  находятся по формулам (рис. 4):
находятся по формулам (рис. 4):
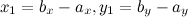
Определение
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Пример
Задание. Найти координаты вектора  , если
, если 
Решение. 
Направляющие косинусы
Определение
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Дляединичного вектора
|
|
|
Если в пространстве задан вектор  , то его направляющие косинусы вычисляются по формулам:
, то его направляющие косинусы вычисляются по формулам:
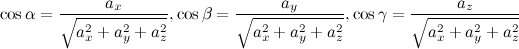
Здесь  ,
,  и
и  - углы, которые составляет вектор с положительными направлениями осей
- углы, которые составляет вектор с положительными направлениями осей  ,
,  и
и  соответственно.
соответственно.
Основное свойство направляющих косинусов
Определение
Сумма квадратов направляющих косинусов равна единице.
1

Если известны направляющие косинусы вектора  , то его координаты могут быть найдены по формулам:
, то его координаты могут быть найдены по формулам:
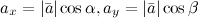
Аналогичные формулы имеют место и в трехмерном случае - если известны направляющие косинусы вектора  , то его координаты могут быть найдены по формулам:
, то его координаты могут быть найдены по формулам:

Дата добавления: 2018-02-15; просмотров: 2155; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
