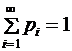По определению математического ожидания находим. Числовые характеристики случайной величины
Числовые характеристики случайной величины
Закон распределения полностью характеризует случайную величину. Однако при практическом изучении случайных величин важную роль играют некоторые числовые характеристики распределения, позволяющие определить среднее значения случайной величины, меру случайного рассеивания возможных значений случайной величины и т.д.
Например, при изучении закона распределения заработной платы работников предприятия прежде всего ставится вопрос о средней заработной плате, а также о коэффициенте ее дифференциации, т. е. о мере случайного рассеивания.
Кроме того, числовые характеристики случайных величин важны и при теоретических исследованиях. Так, по одной или двум числовым характеристикам (среднему значению, дисперсии) можно однозначно восстановить используемые в статистике модельные законы распределения (биноминальной, пуассоновский, нормальный и т.д.).
К важнейшим числовым характеристикам случайной величины относятся математическое ожидание, дисперсия, среднее квадратичное отклонение и т.п.
Математическое ожидание и его свойства.
Рассмотрим дискретную случайную величину, закон распределения которой определяется таблицей
Таблица 1.
| Х |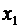 
| 
| … | 
|
|
| 
| 
| … | 
|
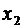
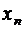
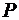
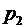
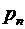
Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятность:
|
|
|
.
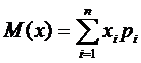Сформулированное определение математического ожидания применяется в том случае, когда множество значений случайной величины конечно. Если множество значений случайной величины счетно, т.е. закон распределения случайной величины задается таблицей 2
Таблица 2.
|
| X |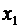
|
| … |
| … |
| |
|
|
|
| … |
| … | , |
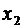
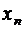
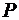
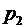
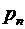
то математическим ожиданием дискретной случайной величины называется ряд
,
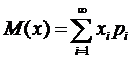при условии, что этот ряд абсолютно сходится.
Если рассматривается неперерывная случайная величина с заданной дифференциальной функцией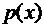 
распределения, то
математическим ожиданием непрерывной случайной величины называется несобственный интеграл первого рода
,
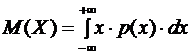при условии, что этот интеграл абсолютно сходится.
Математическое ожидание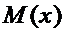 
является величиной постоянной, т.е. представляет числовую характеристику случайной величины, которая имеет размерность совпадающую с размерностью случайной величины.
С вероятной точки зрения математическое ожидание характеризует среднее значение случайной величины.
Для доказательства этого утверждения рассмотрим дискретную случайную величину, закон распределения которой задается таблицей 1
|
|
|
Таблица 1.
| Х |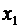
|
| … |
|
|
|
|
|
| … |
|
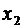
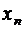
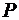
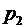
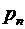
Обозначим через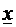 
наименьшее, а через 
наибольшее из всех возможных значений случайной величины. Тогда для любого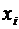 
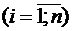выполняется неравенство
.
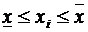
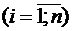Домножим записанные неравенства соответственно на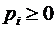 
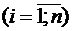и сложим все полученные неравенства, имеем
.
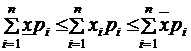Так как постоянный множитель можно выносить за знак суммирования, то из последних неравенств находим
,
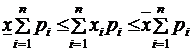откуда с учетом равенства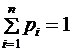 
получаем
. 
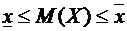Пример 1. Найти математическое ожидание случайной величины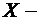 
размера выигрыша в лотереи (см. пример 1 п.3.2), если закон ее распределения задан таблицей
Таблица 3
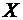
| 0 | 10 | 20 | 50 | |
|
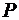
| 0,5 | 0,25 | 0,15 | 0,1 | . |
Решение. Воспользовавшись определением математического ожидания для заданной случайной величины 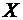, находим
.
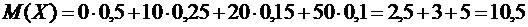Так как средний выигрыш в лотерее составляет 10,5 грн., то цена лотерейного билета должна составлять 10,5 грн.
Свойства математического ожидания
Для упрощения доказательств свойств математического ожидания будем рассматривать случайные величины, множества возможных значений которых конечны. Однако соответствующие свойства справедливы также и для дискретных случайных величин, множества возможных значений которых счетны, и для непрерывных случайных величин. Поэтому при формулировке свойств мы не будем указывать какие из случайных величин рассматриваются.
|
|
|
Свойство 1. Математическое ожидание постоянной величины равняется самой постоянной величине
.
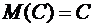Доказательство. Постоянную величину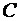 
можно рассматривать как случайную, которая принимает единственное значение 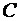с вероятностью 1, то есть имеет закон распределения
|
|
|
|
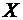
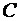
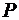
| 1 |
По определению математического ожидания находим
.
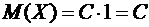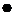
Свойство 2. Постоянный множитель можно выносить за знак ожидания
.
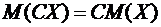Доказательство. Если случайная величина 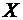задана таблицей 1
Таблица 1.
| Х |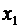
|
| … |
|
| |
|
|
|
| … |
| , |
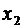
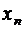
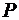
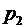
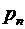
то случайная величина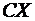 
имеет закон распределения вида
Таблица 2.
|
| 
| 
| … | 
|
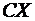
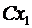
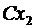
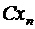
 Мы поможем в написании ваших работ! |