Простейшие свойства вероятности: монотонность, формула сложения, вероятность разности событий.
Случайные события,их классиф.Операции со случ событиями. Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Каждое случайное событие есть следствие действия многих случайных причин Таким образом, события будет рассматривается как результат испытания.Классификация случайных событий. Полной группой событий называются несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. События: 1.совместные,несовместные(неск несовм события – попарно несовместн)2.достоверные,невозможные,случайные3.противоположные.4...События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.5.элиментарн событие-несовм единственновозм обяз исходы испыт,такие,что мн-во….,а др события 0неко подмнож-во. Операции.1.А влечет за соб Б(при А обяз наступ В)если А и В влекут друг-друга,=> равны 2.Сумма-объедин.3.ПРоизвед – пересечение.4.Разн. А –В – Наступ только А,В не наступ.св-ва опер-й1.Коммутат(перестан)2.Ассоциативн -3 и переест скобок.3.Дистрибут А(В+С)= АВ+АС Доп св-ва: 1.А +противоп = Достов.ПРоизвед – невозможн соб-е.2. А+дост=дост , А × дост= А , А+Ø=А ,А× Ø = Ø 3.А+А =А. А×А=А 2.классич, статистич и геометрич опр-е вер-ти .Классическая формула вероятности Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой P(A) = m/n, где m-число элементарных исходов, благоприятствующих А; n-число всех возможных элементарных исходов испытания. Здесь предполагается, что элементарные исходы не совместны, равновозможные и образуют полную группу. Из определения вероятности вытекает следующие свойства: 1.Вероятность достоверного события равна единице. 2.Вероятность невозможного события равна нулю. 3.Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0 <m/n<1, следовательно, 0<P(A)<1. Итак, вероятность любого события удовлетворяет двойному неравенству 0 <= P(A)<= 1. Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности -вероятность попадания точки в область(отрезок, часть плоскости и т.д.). Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P= Длинаl/длинаL Класс Опр-е предполагает,что все элемент исходы равновозможны.Задач ,в кот можно исходить из таких соображ-й мало.т.к. трудно утсатовить,что исходы равновозможны.(относит) частота события – отнош числа опытов,в кот появ это сбыт,к общ чисул опытов. Св-ва:1.от 0 до 1. 2.частота (достоверн) =1.3.W(Ø)=0.4.част 2 несовм событий = сумме частот 2х несовм событий.W(A+B)=W(A)+W(B) .Облад св-вом стат устойч.Стат Вер-ть события-число,ок кот группир знач-я частоты данн события в различн сериях больш числа испытаний.Св-ва: 1.вер-ть(дост)=1.2.невозм – 0.3.случ- между 0 и 1.4.W(A+B)=W(A)+W(B) 3.Элементы комбинаторики: размещения, перестановки и сочетания (вывод формул). Свойства сочетаний. Комбинатор. Изуч спос подсчета числа эл-в в конечн множ-х. Ф-лы исп при вычисл вер-й.Перестан-ки–множ-ва, сост из один эл-в и отлич порядком.число перестан – 0!=1 .Размещ-мн-во,сост из n различн эл-в по m эл-в ,кот отлич либо сотавом эл-в ,либо их порядком. сочет из nразл эл-в по m -мн-ва,содерж m эл-в из числа n данных,и кот отлич хотя бы 1 эл-м . Т о кенечн множ-х:Число всех подмонж=в множ-ва,сост из n эл-в, равно , Числа переест и размещ-й связ рав-вом . Число Размещ-й по m эл-в с повтор из n эл-в равно )c повт.= .Число сочет с поатор из n эл-в по m )повт = Правила комбинатор. 1.Прав суммы. :если нек объект А может быть выбран их множ-ва m способами, а друг В – n способами, то В или А – m+n спос.2.Прав произвед.Если объект А можно выбрать из множ-ва объектов m спос и после кажд так выбора В можно выбрать n спос,то пара объектов(А,И) в указ порядке может быть выбр m×n спос
|
|
|
|
|
|
|
|
|
Вывод формул и св-а сочет-й
1. С катое в степени 0 = С катое в степ к =1
2. С катое в первой = к
3. 
Доказательство. 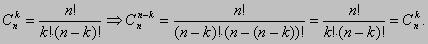
4 . 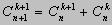 (
( 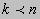 ).
).
Доказательство. 
Последнее свойство позволяет описать процедуру последовательного получения числа сочетаний при различных значениях n и k.
Используя последнее свойство, можно представить число сочетаний в виде так называемого треугольника Паскаля.
5.Геометрическая вероятность Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности -вероятность попадания точки в область(отрезок, часть плоскости и т.д.). Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P= Длинаl/длинаL
|
|
|
Простейшие свойства вероятности: монотонность, формула сложения, вероятность разности событий.
Если А Ì В, то Р(А) £ Р(В), т.е. вероятность монотонна. Представим множество В как В = А + B\A (см. рисунок 1). По построению А(В\А)=Æ, следовательно, события А и В\А несовместны. Поэтому по аксиомам конечной аддитивности* и неотрицательности вероятности имеем Р(В) = Р(А) + Р(В\А) ³ Р(А).
Р(А) £ 1 для любого А Î F. Так как A Ì W, то из свойства монотонности и аксиомы нормировки вероятности следует Р(А) £ Р(W) = 1. Формула сложения и вероятность разности событий:
Р(А+В) = Р(А) + Р(В) – Р(АВ) для любых А, В Î F. Представим А в виде А = А\В + АВ (см. рисунок 2). Очевидно, что события А\В и АВ несовместны. Тогда по аксиоме конечной аддитивности вероятности имеем Р(А) = Р(А\В) + Р(АВ),откуда Р(А\В)=Р(А)-Р(АВ). Аналогичным образом поступим с событием А+В. Имеем А+В = В + А\В, причем события В и А\В несовместны. Тогда из аксиомы конечной аддитивности вероятности следует Р(А+В)=Р(В)+Р(А\В). Подставляя в данное выражение формулу для Р(А\В), получаем требуемое. Р(А+В)=Р(А)+Р(В)-Р(АВ).
* Аксиома: Для любых несовместных событий А и В из F справедливо равенство Р(А + В) = Р(А) + Р(В).
Дата добавления: 2018-02-18; просмотров: 703; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
