Определение нормы стока при недостаточности данных наблюдений с помощью метода корреляции
Вопросвы по гидре на 31 05 16
Определение циклов водности реки по разностной интегральной кривой стока
Представление о циклических колебаниях без эффекта смещения границ между фазами циклов большой и малой продолжительности, по мнению ряда исследователей обеспечивает использование интегральных разностных кривых, или суммарных кривых отклонений от середины. Они могут быть выражены или в абсолютных величинах, например в модульных коэффициентах: sum(k-1) где модульный коэффициент k= qi/q0 участок интегральной кривой с наклоном вверх и с положительным значением величины Sum(k-1) соответствует многоводной фазе циклических колебаний стока, а участок с наклоном вниз и с отрицательным значением Sum(k-1)соответствует маловодной фазе.
Факторы влияющие на величину максимального расхода дождевого паводка
Величина максимальных дождевых расходов воды в основном зависит от интенсивности и продолжительности выпадение дождя и от величины площади, на которую он выпадает. Для рек с малыми бассейнами интенсивные дожди (ливни) вызывают значительные максимальные расходы.
При наличии данных наблюдений строится теоретическая кривая обеспеченности максимальных за каждый год расходов дождевых паводков и по ней определяются расчетные максимальные расходы заданной обеспеченности. При построении этой кривой необходимо учитывать, что многолетняя изменчивость дождевых максимумов значительно больше, чем половодных. В связи с этим рекомендуется принимать соотношение Сs=4Сv.
|
|
|
Характеристики стока
Основные характеристики стока
Для количественной оценки стока рек применяются следующие его характеристики.Объем стока W м3 или км3 — количество воды, протекающее в русле реки через данный замыкающий створ за промежуток времени Т суток,

где Q — средний расход в м3/с за время Т суток; 86400 — число секунд в сутках.
Модуль стока М л/(с*км2) — количество воды, стекающей с единицы площади в единицу времени,

где F — водосборная площадь в км2.
Слой стока Y — слой воды в миллиметрах, равномерно распределенной по площади F и стекающей с водосбора за некоторый промежуток времени Т суток,

Слой стока за год в миллиметрах:

Коэффициент стока h — отношение величины слоя стока с данной площади за некоторый промежуток времени к величине слоя атмосферных осадков, выпадающих на эту площадь за тот же промежуток времени, т. е.
h = Y/X, 0 ≤ h ≤ 1.
Коэффициент стока — величина безразмерная.
Определение нормы стока при наличии данных наблюдений
Среднее значение годового стока за многолетний период при неизменных физико-географических условиях, включающий не менее двух чётных замкнутых циклов колебаний водности называется нормой годового стока.
|
|
|
Формула для расчета нормы стока:
 ,где ∑Q-сумма среднегодовых расходов,N-количество лет наблюдений.
,где ∑Q-сумма среднегодовых расходов,N-количество лет наблюдений.
Путем сложения строк столбца Среднегодовые расходы воды(таблицы 1) и деления полученной суммы на количество строк(30) получаем, что QN=286,93 м3/с.
Существует правило, которое гласит, что норма стока определена достаточно точно, если относительная средняя квадратичная ошибка нормы стока(EQ0)<10%.
Относительная средняя квадратичная ошибка нормы стока(EQ0), вычисляется по формуле:
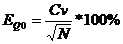 ,
,
Предварительно нужно найти коэффициент вариации (Cv) по формуле:
 , таким образом, Cv=0,2310
, таким образом, Cv=0,2310
Следовательно, EQ0=4,2%. Мы укладываемся в среднею квадратичную ошибку нормы стока<10%. А это может значить только одно, что норма стока определена наиболее точно.
Все дополнительные расчеты отражены в Таблице 1.
По данным Таблицы 1 строится график (График 1), на котором отмечаются маловодные и многоводные периоды, отражающие колебания годового стока.
Определение нормы стока при недостаточности данных наблюдений с помощью метода корреляции
Способ корреляции. В данном случае используется вероятностная зависимость между величинами стока исследуемой реки и реки-аналога. При этом вычисляется коэффициент корреляции по значениям параллельных наблюдений:
|
|
|

где q0-среднее значение за n-лет.
По своей математической сути r может быть в пределах от –1 до 1.
Когда точки ложатся на одну прямую линию то r=1 значит, мы перешли от вероятностной зависимости к однозначной. В этом случае численному значению q0 на реке-аналоге будет соответствовать конкретная величина q0 на исследуемой реке.
На основе полученного численного значения(r), ряд наблюдений для исследуемой реки можно удлинить с помощью уравнения регрессии:

Дата добавления: 2018-02-18; просмотров: 1849; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
