Метод Бокса-Дженкинса (ARIMA)
Методы прогнозирования
Методы сглаживания и скользящие средние
В этом разделе рассматриваются три группы методов прогнозирования временных рядов: наивные, усредняющие и сглаживающие. Наивный метод основан на предположении, что будущее лучше всего характеризуется последними изменениями. Метод усреднения позволяет разработать прогноз, основываясь на среднем значении прошлых наблюдений. Методы сглаживания базируются на усреднении накопленных данных при помощи набора весовых коэффициентов.
Корректный подход к оценке метода прогнозирования включает несколько этапов. Следует выделить пять важных этапов:
- тщательное изучение природы исследуемого объекта или процесса для выбора адекватного метода прогнозирования;
- выделение двух групп среди доступных данных – для разработки прогнозов и для проверки полученных результатов;
- уточнение исходных данных с целью обнаружения ошибок;
- разработка прогнозов и оценка достоверности полученных результатов;
· использование (интерпретация) полученных результатов и выполнение, при необходимости, уточнения и дополнения прогнозов.
Если исходные данные представлены небольшим набором сведений, то наивный метод считается единственно возможным способом прогнозирования. При наивном прогнозировании считается, что последний период лучше всего предсказывает будущее. Самая простая модель наивного прогнозирования основана на следующем соотношении:
|
|
|
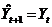. (15.1)
Величина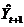 
представляет собой прогноз, сделанный в момент времени 
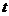(начальное предсказание) для момента времени 
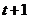. Наивным прогнозом для каждого периода времени является непосредственно предшествующее ему наблюдение. Текущему значению величины в ряду присваивается стопроцентный вес. Поэтому наивный прогноз часто называют "прогнозом без изменений". Фактически, при наивном прогнозировании отбрасываются все старые наблюдения.
В данном случае важно оценить случайные флуктуации исследуемого объекта или процесса. Ошибка прогноза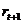 
рассчитывается по очевидной формуле:
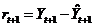. (15.2)
Анализ статистики величин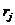 
позволяет сделать вывод о возможности использования наивного метода для исследуемого объекта или процесса. Очевидно, что при стремлении суммы величин 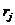к нулю применение наивного прогнозирования может быть оправданно. С другой стороны, условие близости к нулю суммарной ошибки нельзя считать достаточным. Необходимо также чтобы максимальное значение 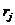не превысило заранее выбранный порог ошибки. Если исследование ряда 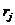указывает на наличие тренда для исследуемого объекта или процесса, то наивный метод не годится для разработки прогностических оценок.
|
|
|
Некоторые прогнозы приходится обновлять регулярно (ежедневно, еженедельно и так далее). Количество хранимой информации резко возрастает. Кроме того, "старая информация" может оказаться бесполезной. В подобных случаях прибегают к усреднению или к сглаживанию. При использовании подобных методик взвешенное усреднение данных, связанных с прошлыми наблюдениями, применяется для сглаживания случайных флуктуаций. Такой подход основан на том, что флуктуации являются случайными отклонениями от некоторой гладкой кривой. Эту кривую и следует определить.
Методы усреднения, в свою очередь, делятся на несколько видов. Используют простые средние, скользящие средние и двойные скользящие средние.
В первом методе в качестве начальных данных используется среднее значение исследуемой величины в момент времени 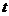, а в качестве тестовой части – остальные. Прогноз 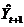осуществляется на основании усреднения начальных данных:
|
|
|
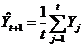. (15.3)
Когда становится известным новое наблюдение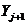 
, оно используется для разработки прогноза 
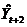. При этом вычисления осуществляются по той же формуле (15.2). Схожесть с методом наивного прогнозирования наблюдается в случае применения искусственного приема, когда сохраняются только "свежие" прогнозы:
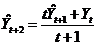. (15.4)
Метод простых средних приемлем в тех случаях, когда исследуемые объекты или процессы стабильны. Характерный пример такой ситуации – объем продаж товара, зависящий от усилий торговой сети (без сезонных колебаний).
В ряде случаев практический интерес представляют только последние наблюдения. Тогда целесообразно фиксировать количество того объема сведений, которое подлежит дальнейшей обработке. Для описания такой модели введен термин "скользящее среднее". Как только новое наблюдение становится доступным, оно включается в усреднение, а наиболее старое исключается. При использовании скользящего среднего порядка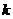 
прогнозируемое значение 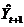определяется таким выражением:
|
|
|
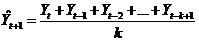. (15.5)
Всем слагаемым в числителе формулы (15.5) присвоен одинаковый вес. Величина 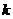не меняется со временем. Модель скользящего среднего не очень удачна с точки зрения учета тренда и сезонных изменений.
Для учета линейного тренда исследуемого объекта или процесса эффективен метод двойных скользящих средних. Сначала вычисляется ряд значений методом скользящих средних, а потом этот же набор прогнозов усредняется тем же методом. Способ расчета двойного скользящего среднего реализуется следующим образом. Прежде всего, выполняются расчеты по формуле (15.5):
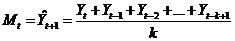. (15.6)
Затем для вычисления вторичного скользящего среднего используется такое выражение:
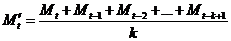. (15.7)
Далее к первичному скользящему среднему прибавляется разница между первичным и вторичным скользящими средними:
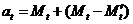. (15.8)
Определяется коэффициент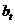 
, входящий, наряду с постоянной величиной 
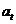, в уравнение прогностической прямой:
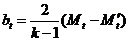. (15.9)
Теперь для количества периодов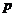 
уравнение прогностической прямой представимо в такой форме:
. (15.10)
Метод экспоненциального сглаживания подразумевает использование взвешенных (экспоненциально) скользящих средних. Данная модель обычно применяется в том случае, когда факт наличия тренда и не подтвержден, и не опровергнут. Более новым данным присваивается больший вес. Если для последнего наблюдения был установлен вес 
, то для предыдущего он равен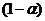 
, а для того, который ему предшествовал, – 
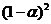и так далее. Вес выбирается так, чтобы соблюдалось неравенство 
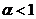. Если требуется стабильность прогнозируемых значений, то необходимо выбирать малое значение . Большое значение позволяет быстро реагировать на возникающие изменения. Вероятно, такая возможность обусловила вхождение экспоненциального сглаживания в группу адаптивных методов прогнозирования.
Экспоненциальное сглаживание можно рассматривать как процедуру постоянного пересмотра результатов прогнозирования с учетом результатов последних наблюдений. Существуют различные разновидности экспоненциального сглаживания: метод Хольта, метод Винтерса и другие.
Простая линейная регрессия
Некоторые переменные связаны между собой линейной зависимостью. Этот закон может быть обусловлен природой анализируемых переменных. В ряде случаев предположение о линейной зависимости допустимо на небольшом интервале изменения аргумента аппроксимирующей функции.
Линейная зависимость двух переменных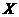 
и 
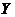может быть установлена при помощи корреляционного анализа. Сила линейной зависимости определяется коэффициентом корреляции 
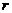. Если имеется 
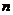значений для пар исследуемых переменных, то выборочный коэффициент корреляции определяется следующим образом:
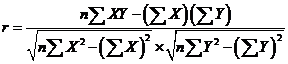. (15.11)
Если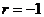 
, то исследуемые величины связаны между собой совершенной отрицательной зависимостью. Напротив, при 
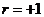между исследуемыми величинами установлена совершенная положительная зависимость. Соответствующие примеры приведены на рисунке 15.1 – варианты (a) и (b). Два следующих варианта иллюстрируют случаи несовершенной линейной зависимости (положительной и отрицательной). Они наиболее интересны с практической точки зрения. Вариант (e) представляет собой пример нелинейной зависимости. В процессе исследования информации может быть установлено отсутствие зависимости – вариант (f).
Рис. 15.1. Примеры корреляции
Формула прогностической кривой имеет такой вид:
. (15.12)
Величина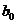 
называется свободным членом, а 
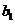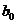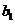– угловым коэффициентом. Величины и определяются методом наименьших квадратов. Соответствующие формулы были приведены в одиннадцатой лекции. Значения 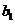и 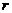пропорциональны друг другу и имеют один и тот же знак.
Для набора пар 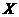и 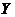в качестве наилучшего приближения выбирается прямая, для которой сумма квадратов отклонений по оси 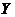минимальна. Эта прямая называется прямой регрессией, а ее уравнение – вида (15.12) – уравнением регрессии.
После получения уравнения регрессии необходимо определить ошибку аппроксимации набора пар 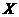и 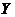при помощи кривой. Стандартная ошибка оценки 
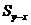вычисляется по следующей формуле:
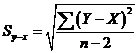. (15.13)
Для сравнительно больших выборок следует ожидать, что около 67% (две трети) разностей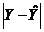 
не будет превышать 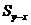и примерно 95% этих те разностей будет не более, чем 
.
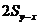Линейная регрессия может быть использована и в случае преобразования переменных, если такая операция приводит к линейной зависимости. Для создания новых независимых переменных часто используют четыре типа преобразований:
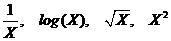. (15.14)
Метод прогнозирования, рассмотренный в этом разделе, дополнен для тех случаев, когда необходимо учитывать влияние нескольких независимых переменных. Такой метод называется многомерным регрессионным анализом.
Метод Бокса-Дженкинса (ARIMA)
Изменения объекта или процесса в различные периоды времени часто взаимосвязаны. Эта зависимость измеряется при помощи коэффициента автокорреляции. Для запаздывания на 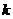периодов этот коэффициент 
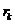между наблюдениям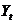и 
и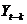 
рассчитывается по такой формуле:
. (15.15)
Верхний предел суммирования 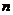определяет общее количество наблюдений.
Для прогнозирования иногда используются модели, в которых анализируется временная структура данных. Модели смешанного авторегрессионного скользящего среднего (AutoRegressive Integrated Moving Average – ARIMA) хорошо описывают как стационарные, так и нестационарные временные ряды. В стационарных рядах результаты изменяются относительно некого среднего значения. В нестационарных рядах не существует постоянного среднего значения.
В моделях ARIMA для прогнозирования используется информация, которая содержится в исследуемых исходных данных. Модель ARIMA опирается на автокорреляционную структуру данных. В изучение этих моделей значительный вклад внесли G.E.P. Box и G.M. Jenkins. По этой причине построение моделей ARIMA и прогнозирование на их основе часто называют методом Бокса-Дженкинса.
Общая идея выбора модели прогнозирования, которая была предложена G.E.P. Box и G.M. Jenkins, показана на рисунке 15.2. Этот рисунок отражает только основные моменты рассматриваемого метода.
Рис. 15.2. Алгоритм выбора модели для метода G.E.P. Box и G.M. Jenkins
Метод ARIMA основан на итеративном подходе к выбору приемлемой модели среди возможных вариантов. Такой подход позволяет избежать существенных ошибок, которые возникают вследствие случайного характера отдельных результатов наблюдений.
В настоящее время метод Бокса-Дженкинса реализован практически во всех пакетах программ, используемых для прогнозирования. Появляются модификации данного метода, позволяющие повысить точность прогностических оценок.
Дата добавления: 2018-02-15; просмотров: 1140; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!