Примеры решения задач по выбору структуры сети
Структура сети
Общие сведения из теории графов
Самые первые системы телефонной связи не использовали коммутационные станции. Пример такого решения показан в левой части рисунка 8.1. Для связи с телефонным аппаратом вызываемого абонента используется соответствующий ключ. Совокупность таких ключей можно рассматривать как концентратор. Существенный недостаток подобного способа организации связи – значительное количество линий, включаемых на выходе концентратора. Для связи с 
абонентами в каждый концентратор необходимо включить 
линий.
Рис. 8.1. Два варианта организации телефонной связи для четырех абонентов
Очевидно, такой способ организации связи не позволяет связывать большое количество терминалов. В правой части рисунка 8.1 изображен вариант организации связи, который подразумевает установку коммутационной станции. В этом случае от каждого терминала к станции прокладывается только одна линия.
Для варианта организации связи без установки коммутационной станции основные затраты обусловлены количеством прокладываемых линий. Стоимостью концентратора (набором ключей) можно пренебречь. Общее количество линий 
для связи абонентов определяется следующим образом:
. (8.1)
Затраты на организацию линий 
пропорциональны их количеству и средней длине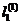 
. Вводя коэффициент пропорциональности 
, можно записать такое соотношение:
|
|
|
. (8.2)
Затраты на реализацию второго варианта организации связи 
складываются из стоимости коммутационной станции 
и линий, число которых равно . Средняя длина этих линий 
будет отличаться, значение коэффициента можно считать неизменным. Тогда величина определяется по следующей формуле:
. (8.3)
Второй вариант организации связи предпочтительнее, если выполняется неравенство 
. Формулы (8.2) и (8.3) позволяют только оценить величины и с учетом принятых допущений. На самом деле вычисление стоимостных зависимостей выполняется с учетом большего числа переменных.
Для определения термина "структура сети" целесообразно использовать математическую модель в виде графа. Граф состоит из совокупности вершин, которые соединяются при помощи ребер. Обычно вершинам графа ставятся в соответствие коммутационные станции или терминалы. Линии связи удобно представлять ребрами графа. Примеры различных графов с шестью вершинами приведены на рисунке 8.2. Вершины графа обозначены символами 
.
|
|
|
Рис. 8.2. Четыре примера структур для графа с шестью вершинами
Вариант (a) иллюстрирует граф звездообразной структуры. Центром графа является вершина 
. Граф древовидной структуры показан как вариант (b). Вариант (c) соответствует кольцевой топологии. Граф, в котором все вершины попарно связаны между собой, называется полносвязным (mesh). Такой граф показан как вариант (d).
Вершины графа, соединенные ребрами, называются смежными. Для варианта (a) все вершины с номерами 1, 2, 4, 5, 6 являются смежными только с вершиной . Для кольцевой топологии – вариант (c) – для каждой вершины 
смежными всегда будут две вершины: 
и 
(в данном случае – для шестой вершины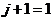 
).
Количество ребер, инцидентных вершине, называется рангом вершины. Например, все вершины в полносвязном графе имеют ранг, который на единицу меньше, чем общее число вершин. Для звездообразной структуры ранг вершины равен пяти (в общем случае он также на единицу меньше общего числа вершин), а все остальные вершины имеют ранг, равный единице. Такие вершины называются тупиковыми – через них не проходит ни один транзитный путь. Ребро, которое начинается и заканчивается в одной и той же вершине именуется петлей. Обычно, в теории сетей связи математические модели в виде графов с петлями не используются.
|
|
|
Путем 
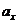между вершинами 
и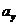 
называется упорядоченная последовательность ребер. В ней каждая вершина графа может встречаться только один раз. Ранг пути для каждой пары вершин обычно определяется количеством, через которые эти вершины связаны между собой. Очевидно, что для полносвязного графа ранг пути равен единице. Для древовидной топологии – вариант (b) – для вершин 
и 
ранг пути равен четырем.
Ребро между вершинами и обозначается различными способами. Чаще всего встречаются три символа: 
(пропускная способность, стоимость), 
(длина) и 
(надежность).
Иногда в сетях информация может передаваться только в одном направлении. Тогда используется модель в виде ориентированного графа – вариант (a) на рисунке 8.3. В ориентированном графе каждое ребро снабжено стрелкой (одной или двумя) для указания на направления связи. Если граф является неориентированным, то стрелки не используются. Пример такого графа показан как вариант (б). Вариант (в) иллюстрирует пример смешанного графа. В нем используются как ориентированные, так и неориентированные ребра.
|
|
|
Рис. 8.3. Ориентированный, неориентированный и смешанный графы
Одна из классических задач выбора структуры сети, решаемая с помощью теории графов, связана с нахождением точки Штейнера. Эта точка позволяет построить древовидную топологию, в которой сумма длин ребер минимальна. Для графа с тремя вершинами, которые образуют равносторонний треугольник, точка Штейнера образуется линиями, сходящимися под углом 120 градусов – рисунок 8.4. Для графа произвольной структуры разработаны алгоритмы поиска точки Штейнера.
Рис. 8.4. Пример нахождения точки Штейнера
Постановка задачи
При выборе структуры сети связи общего пользования, в первую очередь, необходимо выделить естественные уровни иерархии. Процесс выделения этих уровней иллюстрирует рисунок 8.5. На этом рисунке показаны пять уровней иерархии. Естественными уровнями следует считать: международную и национальную сети. Такой принцип принят всеми международными организациями. Следующие естественные уровни иерархии включают региональные и местные (городские и сельские) сети. Такая практика выделения иерархических уровней принята Администрациями связи всех стран за исключением государств с очень маленькой территорией. Выделение сетей доступа – в дополнение к городским и сельским сетям – осуществляется искусственно. Это объясняется удобством анализа и синтеза структуры сети общего пользования на разных уровнях ее иерархии.
Рис. 8.5. Иерархические уровни в сети общего пользования
Выделение ряда иерархических уровней в сети связи базируется на двух основных принципах. Во-первых, учитываются внешние факторы, которые больше всего связаны с административным делением страны и ее регионов. В конечном счете, эти факторы имеют экономическое обоснование, но оно напрямую не связано с оптимизацией стоимости сети связи. Во-вторых, учитываются внутренние факторы, которые нацелены на минимизацию стоимости сети 
при соблюдении ряда ограничений на технические показатели ее функционирования.
Величина есть функция нескольких переменных ( 
) Таким образом при выборе структуры сети на всех уровнях ее иерархии решается задача, которую можно представить в таком виде:
. (8.4)
Для каждой переменной, входящей в формулу (8.4) заданы ограничения, которые обычно могут быть сформулированы в виде неравенств:
. (8.5)
Характерные примеры переменных вида 
могут быть представлены таким перечнем:
· количество независимых путей между каждой парой узлов сети ( 
) должно быть не меньше двух ( 
);
· вероятность потери вызова ( 
) не должна превышать пороговое значение 0,1% ( 
);
· время восстановления неисправности при обрывах линии связи ( 
) не должно быть более одних суток ( 
).
Существует несколько методов решения задачи для выбора структуры сети по критерию (8.4). В большинстве случаев оптимизационную задачу невозможно решить точно. Чаще используют приближенные методы, позволяющие получить решение с приемлемой для практики точностью.
Одна из первых задач, сформулированных практическими требованиями, заключается в нахождении оптимальной емкости коммутационной станции. Критерий оптимальности может быть сформулирован так: найти минимальную стоимость сети в расчете на одного пользователя. Искомая величина складывается из трех основных компонентов:
· стоимость коммутационного оборудования;
· стоимость абонентских линий;
· стоимость соединительных линий.
Поведение соответствующих величин при изменении емкости местной станции показано на рисунке 8.6. Верхняя кривая иллюстрирует поведение суммарных затрат. Очевидно, что эта функция имеет минимум, который достигается при оптимальном значении емкости местной станции 
.
Рис. 8.6. Выбор оптимальной емкости АТС
Обычно, все три зависимости, определяющие величину , могут быть выражены непрерывными функциями 
, зависящими от ( 
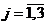). Тогда для нахождения оптимального значения необходимо решить уравнение следующего вида:
. (8.6)
Если для полученного решения вторая производная исследуемой функции положительна, то был получен ее минимум. Отрицательный знак свидетельствует о нахождении максимума исследуемой функции.
Решение подобных задач позволяет построить сеть связи, которая будет оптимальная к тому моменту времени, когда разработан перечень исходных данных. Через некоторое время в сети могут появиться требования, которые невозможно было учесть заранее. Ряд подобных случаев может быть предусмотрен в процессе разработки прогнозов развития сети. Этому аспекту планирования сети посвящена пятнадцатая лекция. Тем не менее, Оператору сети приходится сталкиваться с проблемами, которые заранее предусмотреть невозможно. В подобных случаях возникает ряд новых задач, среди которых целесообразно акцентировать внимание на двух аспектах:
· выбор структуры сети, которая остается близкой к оптимальному решению при различных изменениях требований к сети;
· решение оптимизационной задачи для дальнейшего развития сети, которая была построена не самым рациональным способом.
Именно эти две задачи выбора структуры сети связи становятся самыми актуальными на современном этапе развития инфокоммуникаций. Это утверждение объясняется тем, что сети электросвязи на всех уровнях иерархии уже построены. Для Операторов связи важно определить эффективные пути модернизации эксплуатируемых сетей.
Примеры решения задач по выбору структуры сети
Одна из важных задач модернизации эксплуатируемых сетей связана с доступом. В частности, Операторы ТФОП строили сети доступа как совокупность абонентских линий. Для реализации сетей доступа применялись, в основном, многопарные кабели. Типичная структура сети доступа показана в левой части рисунка 8.7. В этой сети доступа не используются выносные концентраторы (К).
Рис. 8.7. Изменение структуры сети доступа
Каждый из четырех телефонных аппаратов, показанных на рассматриваемом рисунке, включен в АТС индивидуальной абонентской линией, длина которой равна 
( 
). В настоящее время такой способ построения сети доступа становится препятствием для дальнейшего развития инфокоммуникационной системы в целом. Характерный пример – применение технологий xDSL, которые критичны к длине абонентских линий. Проблемы обычно не возникают для абонентской линии с длиной 
. По этой причине короткие абонентские линии при модернизации сети доступа остаются в эксплуатации.
Одно из разумных решений задач, возникающих в процессе модернизации сетей доступа, заключается в установке выносных модулей – правая часть рисунка 8.7. Выносные модули (концентраторы) присоединяются к АТС кабелями с оптическими волокнами (Fiber optic). Их длина обозначена как 
. В результате существенно сокращается длина двухпроводных абонентских линий – с до 
. Предполагается, что 
. Такая гипотеза правомерна при прокладке новых кабелей в существующей канализации.
Для трех модернизируемых направлений задача минимизации стоимости сети доступа решается самостоятельно. Это означает, что надо найти минимум трех функций стоимости 
( ):
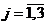. (8.7)
Можно попытаться найти зависимость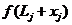 
в виде непрерывной функции. Тогда поставленная задача решается методом, изложенным в конце предыдущего раздела. С практической токи зрения целесообразно использовать иной подход. На участке между АТС и ТА существует всего 
точек, в которых может быть установлен выносной модуль – рисунок 8.8. Обычно 
. В этом случае минимум стоимости целесообразно находить перебором возможных вариантов установки выносного модуля.
Рис. 8.8. Возможные места размещения выносного модуля
Следует учитывать, что при использовании метода перебора возможных вариантов необходимо четко определить все возможные ограничения. Как правило, основным ограничением становится допустимая длина двухпроводной абонентской линии. Это означает, что задается максимальное значение для величины .
Рассмотренный пример связан только с одной задачей модернизации сети доступа. Для решения ряда других задач метод перебора вариантов не применим из-за большого объема анализируемых данных. В подобных случаях применяются методы оптимизации, позволяющие найти решения, близкие к оптимальным.
Второй пример задачи, относящейся к выбору структуры сети, связан с обеспечением инфокоммуникационной системы транспортными ресурсами. В последнее время наблюдается тенденция постоянного роста количества каналов и широкополосных трактов, используемых для предоставления различных инфокоммуникационных услуг. Кроме того, возрастают требования к надежности транспортных ресурсов. Эти факторы стимулируют поиск новых структур транспортной сети.
Эффективное решение было найдено в процессе установки оборудования SDH (Синхронная цифровая иерархия). Высокая пропускная способность трактов SDH могла быть экономично использована только в кольцевых сетях. Эта структура отличается также высокой надежностью (данный вопрос будет рассматриваться в шестнадцатой лекции). На рисунке 8.9 показаны два варианта организации кольцевой сети для объединения шести узлов. Очевидно, что необходимо найти такую кольцевую топологию, для реализации которой требуются минимальные инвестиции.
Рис. 8.9. Два варианта построения кольцевой сети
Перебор всех возможных вариантов построения кольца возможен в двух случаях. Во-первых, для графа с небольшим числом вершин такая процедура не займет много времени. Во-вторых, существуют ограничения на возможные соединения для каждой пары вершин. Это также существенно снижает общее количество рассматриваемых вариантов.
Еще один вид ограничений связан с надежностью кольца. Для обеспечения требуемого коэффициента готовности ограничивается численность вершин в кольце. В этом случае приходится выделять несколько колец в составе транспортной сети. Для решения данной проблемы может быть использован метод "Северо-западного угла". Он разработан для решения так называемой транспортной задачи. Пример использования данного алгоритма показан на рисунке 8.10.
Рис. 8.10. Пример выделения нескольких колец
Сплошными линиями показаны существующие трассы кабельной канализации. Пунктирные линии показывают те направления кабельной канализации, которые могут быть созданы при выполнении условия, что стоимость реализации ребра графа 
является конечной величиной. Это означает, что 
. Символ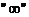 
указывает на тот факт, что строительство кабельной канализации невозможно.
Схожесть предлагаемого алгоритма с методом "Северо-западного угла" состоит в том, что поиск возможных вариантов выделения колец начинается с вершины, расположенной в левой верхней части графа. Этой вершине в рассматриваемой модели присвоен второй номер. Она может быть соединена только с пятой, седьмой или одиннадцатой вершинами. Определение перечня возможных путей, приводящих к образованию кольца, должно быть сделано для всех вершин, которыми заканчиваются трассы кабельной канализации.
Дата добавления: 2018-02-15; просмотров: 684; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!