Градиентный метод в сочетании с методом наискорейшего спуска.
Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы. Допустимый и оптимальный режимы
Оптимизация – задача выявления оптимального процесса из числа прочих, сопоставляемых по критерию оптимальности.
В оптимизации можно выделить:
1. определение оптимальной стратегии развития энергосистем - сооружение или реконструкция систем электроэнергетики и отдельных объектов (выбор месторасположения и мощности, установление сроков ввода в эксплуатацию новых электростанций, подстанций и ЛЭП;
2. выбор наилучшей конфигурации электрических сетей;
3. распределение нагрузок между отдельными электростанциями работающей или проектируемой системы;
4. выбор стратегии наилучшего использования материальных ресурсов (видов топлива и т. д.);
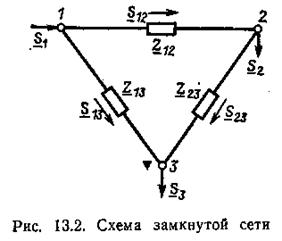
 Уравнения установившегося режима W (X,Y) = 0 связывают между собой параметры установившегося режима электроэнергетической системы. Обозначим совокупность этих параметров вектор - столбцом Z=( Z1, Z2, ..., Zm).При расчете установившегося режима параметры режима Z делятся на заданные независимые Y и неизвестные зависимые X переменные. Число уравнений установившегося режима в системе W (X,Y) = 0 2n равно числу зависимых параметров режима X. Число т параметров режима Z, входящих в уравнение W (X,Y) = 0, больше 2n— числа этих уравнений. Такие системы уравнений называются недоопределеннымн. Избыток числа переменных по сравнению с числом уравнений физически означает, что электроэнергетическая система имеет т—2n степеней свободы. Наличие степени свободы позволяет регулировать режим. Например, пусть имеется система из двух станций и одного нагрузочного узла (см. рисунок).
Уравнения установившегося режима W (X,Y) = 0 связывают между собой параметры установившегося режима электроэнергетической системы. Обозначим совокупность этих параметров вектор - столбцом Z=( Z1, Z2, ..., Zm).При расчете установившегося режима параметры режима Z делятся на заданные независимые Y и неизвестные зависимые X переменные. Число уравнений установившегося режима в системе W (X,Y) = 0 2n равно числу зависимых параметров режима X. Число т параметров режима Z, входящих в уравнение W (X,Y) = 0, больше 2n— числа этих уравнений. Такие системы уравнений называются недоопределеннымн. Избыток числа переменных по сравнению с числом уравнений физически означает, что электроэнергетическая система имеет т—2n степеней свободы. Наличие степени свободы позволяет регулировать режим. Например, пусть имеется система из двух станций и одного нагрузочного узла (см. рисунок).
|
|
|
Предположим, что уравнения установившегося режима имеют вид баланса мощностей для нагрузочного узла, т. е. РГ1 + РГ2 + РН3 = 0; QГ1 + QГ2 + QН3 = 0.
Нагрузки РН3, QН3 заданы. Два уравнения баланса Р и Q содержат четыре переменные. Эти уравнения можно удовлетворить при различных сочетаниях РГ1и РГ2, QГ1и QГ2. Две из этих мощностей можно задавать произвольно в пределах между минимально и максимально возможными их значениями. Остальные мощности будут определены из условий баланса. В данном случае система имеет две степени свободы.
1.2 Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы. Допустимый и оптимальный режимы
Степени свободы определяются возможностью регулирования Р и Q станций, наличием регулируемых трансформаторов, возможностью включения и отключения оборудования и т. д. Именно наличие степеней свободы и определяет существование множества возможных режимов, удовлетворяющих заданной нагрузке потребителей. Среди режимов этого множества практический интерес представляют лишь допустимые режимы, при которых параметры режима остаются в допустимых пределах. Цель управления — среди допустимых режимов найти наиболее экономичный.
|
|
|
При оптимизации за счет наличия степеней свободы параметров режима, т. е. в результате возможности их изменения, выбираются такие значения параметров режима, которые обеспечивают меньшие суммарные потери активной мощности в сети или меньший суммарный расход условного топлива.
Допустимый режим должен удовлетворять условиям надежности электроснабжения и качества электроэнергии. При расчетах допустимых режимов условия надежности электроснабжения и качества электроэнергии учитываются в виде ограничений-равенств и неравенств на контролируемые параметры режима.
Оптимальный режим — это такой из допустимых, при котором обеспечивается минимум суммарного расхода условного топлива при заданной в каждый момент времени нагрузке потребителей.
Наиболее часто решаются оптимизационные задачи трех видов:
Оптимизация режима энергосистем по Р тепловых электростанций, или распределение активных мощностей между тепловыми станциями, позволяет найти активные мощности станций, соответствующие минимуму суммарного расхода условного топлива на тепловых электрических станциях с приближенным учетом потерь в сети при заданных нагрузках потребителей.
|
|
|
Оптимизация режима электрической сети приводит к уменьшению потерь активной мощности в результате оптимального выбора напряжений узлов, реактивной мощности источников и коэффициентов трансформации регулируемых трансформаторов и автотрансформаторов при учете технических ограничений.
Комплексная оптимизация режима позволяет находить оптимальные значения как активных мощностей станций, так и генерируемых реактивных мощностей, а также модулей и фаз напряжений в узлах сети при учете технических ограничений.
2 Применение метода множителей Лагранжа при решении задач оптимизации в электроэнергетике
Этот метод позволяет отыскать условный (относительный) экстремум непрерывной функции, являющейся максимумом или минимумом при выполнении дополнительных условий в форме равенств (уравнений связи).
Метод множителей Лагранжа дает возможность найти такую систему уравнений, которой должен удовлетворять экстремум функции f (X1,..., Xm)на множестве N, определяемом системой уравнений gi (X)для i=1, 2, ..., т.
|
|
|
Для того чтобы найти точку экстремума, характеризующуюся на множестве N неким вектором X, необходимо найти т чисел λ1,…, λm, которые вместе с вектором X удовлетворяли бы следующей системе (т+п) уравнений с (т+п) неизвестными:  ; j = 1,…,n;
; j = 1,…,n; 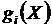 =0; i = 1,…,m.
=0; i = 1,…,m.
Эти уравнения получены как условия экстремума функции Лагранжа 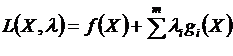 , где числа λ1,…, λm называются множителями Лагранжа.
, где числа λ1,…, λm называются множителями Лагранжа.
Задача заключается в применении метода Лагранжа к определению наивыгоднейших режимов энергетических установок, в частности к нахождению оптимального распределения нагрузки между несколькими агрегатами. Например, если котельная, имеющая п котлов, должна выдать тепло в количестве Q, а расход топлива Вi на каждом i-м котле известен, то минимум суммарного расхода топлива устанавливается с помощью метода Лагранжа, позволяющего найти экстремальное значение целевой функции. Для этого, приравнивая нулю частные производные функции Лагранжа, находbv, что условием относительного минимума суммарного расхода топлива будет одинаковость (idem) относительных приростов расхода топлива всех агрегатов, т. е. величин 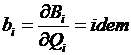 .
.
3.1 Оптимальное распределение перетоков мощности в замкнутых контурах электрической сети
Оптимизация распределения мощностей в замкнутом контуре - это частная задача оптимизации режима электрической сети. Будем считать, что в узлах сети заданы неизменные токи, т. е. уравнения установившегося режима линейны. Если в узлах заданы неизменные мощности, то будем определять их по номинальному напряжению: 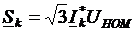 (1) , где
(1) , где 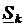 ,
,  - заданные комплексные мощность и ток в каждом узле;
- заданные комплексные мощность и ток в каждом узле; 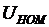 - номинальное напряжение сети.
- номинальное напряжение сети.
При этом ток в ветви kj определяется следующим образом:  . (2)
. (2)
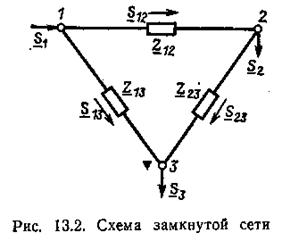 При выполнении условий (1) или (2) уравнения установившегося режима остаются линейными, т. е. вместо заданных комплексных токов в узлах можно использовать комплексные мощности в узлах, а вместо токов в ветвях — мощности в ветвях.
При выполнении условий (1) или (2) уравнения установившегося режима остаются линейными, т. е. вместо заданных комплексных токов в узлах можно использовать комплексные мощности в узлах, а вместо токов в ветвях — мощности в ветвях.
Найдем распределение мощностей в сети на рис. 13.2, соответствующее наименьшим потерям активной мощности, при выполнении первого закона Кирхгофа для мощностей при условии (1). Иными словами, определим такие значения мощностей в линиях 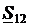 ,
, 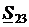 ,
, 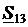 , которые соответствуют минимуму потерь активной мощности в сети min ΔP при выполнении следующих ограничений-равенств первого закона Кирхгофа для узлов 2 и 3:
, которые соответствуют минимуму потерь активной мощности в сети min ΔP при выполнении следующих ограничений-равенств первого закона Кирхгофа для узлов 2 и 3: 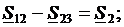
 или для активных и реактивных мощностей:
или для активных и реактивных мощностей:
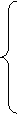
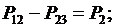
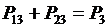 ;
;
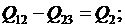 (3)
(3)
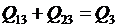 ;
;
Потери активной мощности в сети на рис. 13.2 с учетом условия (2) равны 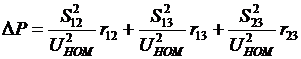 .
.
Условие минимума потерь запишем так:
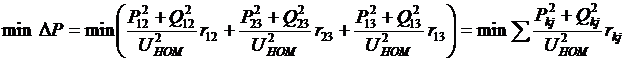 (4)
(4)
3.2 Оптимальное распределение перетоков мощности в замкнутых контурах электрической сети
Потери мощности, записанные в таком виде — это целевая функция задачи оптимизации режима сети, условия (3)—это ограничения-равенства первого закона Кирхгофа. Задача (3), (4) - одна из простейших формулировок задачи оптимизации режима электрической сети.
Система ограничений (3) содержит четыре уравнения и шесть неизвестных активных и реактивных потоков мощности в ветвях P12, P13, P23, Q12, Q13, Q23. Она имеет бесконечное множество решений. Можно задать любые значения, например, четырех потоков P13, Р23, Q13,Q23 и из (3) найти значения потоков P12, Q12, удовлетворяющие первому закону Кирхгофа. Параметры режима имеют две степени свободы. Изменяя параметры режима, можно найти такие их значения, при которых потери мощности ΔР в сети минимальны.
Определим потоки мощности, соответствующие минимуму потерь. Для этого выразим P13, Р23, Q13,Q23 из (3) через неизвестные потоки Р12, Q12 и заданные нагрузки в узлах:
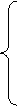
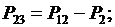

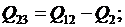 (5)
(5)
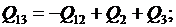
Подставим (5) в целевую функцию (4) и выразим потери через два неизвестных потока Р12 и Q12:
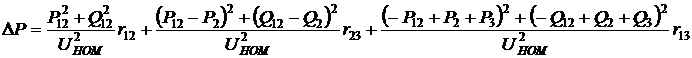 .
.
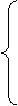 Получили целевую функцию, которая зависит только от двух неизвестных Р12 и Q12. При этом задача определения условного экстремума функции шести неизвестных сведена к отысканию безусловного экстремума функции двух переменных. Последний определяется из условия равенства нулю частных производных от ΔР по Р12 и Q12:
Получили целевую функцию, которая зависит только от двух неизвестных Р12 и Q12. При этом задача определения условного экстремума функции шести неизвестных сведена к отысканию безусловного экстремума функции двух переменных. Последний определяется из условия равенства нулю частных производных от ΔР по Р12 и Q12:

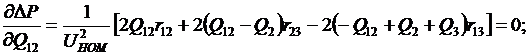
Решив эти уравнения, получим следующие аналитические выражения для оптимальных потоков мощности Р12 и Q12.


4.1 Применение метода множителей Лагранжа для оптимизации перетоков мощности в электрической сети
Применение метода Лагранжа для решения задачи оптимального распределения потоков мощности в сети состоит в определении минимума функции Лагранжа, в которую входят потери активной мощности
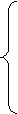
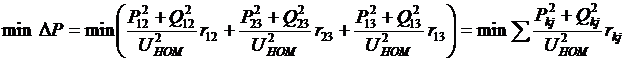 и уравнения первого закона Кирхгофа (1):
и уравнения первого закона Кирхгофа (1):
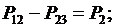
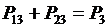 ;
;
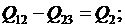
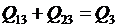 ; каждое из которых умножается на соответствующий множитель Лагранжа. Рассмотрим задачу оптимизации режима сети на рис. 13.2, когда потоки реактивной мощности в линиях Qkj равны нулю.
; каждое из которых умножается на соответствующий множитель Лагранжа. Рассмотрим задачу оптимизации режима сети на рис. 13.2, когда потоки реактивной мощности в линиях Qkj равны нулю.
Равенство нулю потоков Q в линиях 12, 23, 31 означает, что в узлах 2 и 3 на рис. 13.2 имеет место полная компенсация реактивной мощности. Необходимо определить 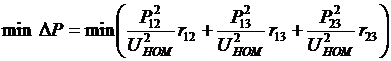 (2)
(2)
при выполнении двух ограничений равенств из (1)


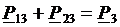 . (3)
. (3)
Функция Лагранжа
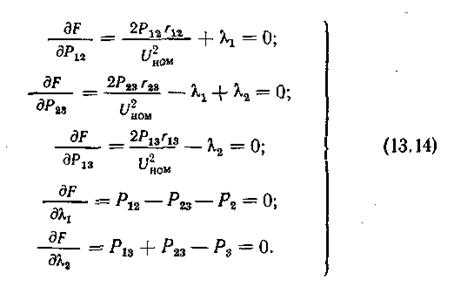
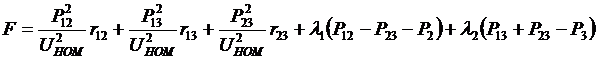 , где
, где 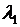 и
и 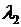 - множители Лагранжа.
- множители Лагранжа.
|
4.2 Применение метода множителей Лагранжа для оптимизации перетоков мощности в электрической сети
множителей Лагранжа 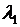 и
и 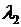 . Минимум функции Лагранжа соответствует решению исходной задачи и определяется равенством нулю пяти частных производных:
. Минимум функции Лагранжа соответствует решению исходной задачи и определяется равенством нулю пяти частных производных:
Для решения системы линейных алгебраических уравнений (4) преобразуем ее первые три уравнения в уравнение второго закона Кирхгофа, исключив из них множители Лагранжа. В результате получим выражение:
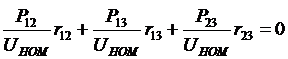 .
.
Решая два последних уравнения системы (4) совместно с этим уравнением, получим
 .
.
Отсюда  .
.
5.1 Оптимизация распределения перетоков мощности сложной электрической сети
Оптимизация распределения мощностей в сложной сети при выполнении первого закона Кирхгофа приводит к распределению потоков мощности в сети только с активным сопротивлением.
 Рассмотрим самый простой случай, когда все потоки Q равны нулю. Потери активной мощности в сети являются квадратичной формой потоков активной мощности в линиях, которую можно записать следующим образом:
Рассмотрим самый простой случай, когда все потоки Q равны нулю. Потери активной мощности в сети являются квадратичной формой потоков активной мощности в линиях, которую можно записать следующим образом:  (1), где РВ — вектор - столбец потоков активных мощностей в ветвях, порядок которого равен числу ветвей т; индекс «т» означает транспонирование; RB — диагональная матрица активных сопротивлений ветвей порядка т, l-й элемент которой равен активному сопротивлению l-й ветви.
(1), где РВ — вектор - столбец потоков активных мощностей в ветвях, порядок которого равен числу ветвей т; индекс «т» означает транспонирование; RB — диагональная матрица активных сопротивлений ветвей порядка т, l-й элемент которой равен активному сопротивлению l-й ветви.
Для сети на рис. 13.2 потери мощности можно записать
в таком виде:
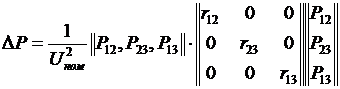 .
.
Первый закон Кирхгофа можно записать: 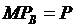 (2), где Р - вектор-столбец активных мощностей в узлах, порядок которого равен числу независимых узлов п; М — первая матрица инциденций, число строк которой равно п, а число столбцов — числу ветвей т. Для сети на рис. 13.2
(2), где Р - вектор-столбец активных мощностей в узлах, порядок которого равен числу независимых узлов п; М — первая матрица инциденций, число строк которой равно п, а число столбцов — числу ветвей т. Для сети на рис. 13.2
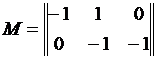 и первый закон Кирхгофа
и первый закон Кирхгофа 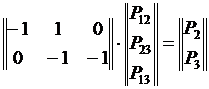
Задача оптимизации 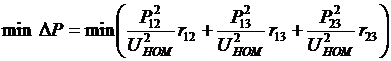 и
и
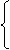

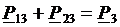 в матричном виде имеет вид: определить
в матричном виде имеет вид: определить 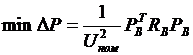 (3) при выполнении условия (2). Это задача квадратичного программирования, так как целевая функция (1) - квадратичная форма, а ограничения (2) - система линейных алгебраических уравнений. Запишем функцию Лагранжа в матричном виде:
(3) при выполнении условия (2). Это задача квадратичного программирования, так как целевая функция (1) - квадратичная форма, а ограничения (2) - система линейных алгебраических уравнений. Запишем функцию Лагранжа в матричном виде:
5.2 Оптимизация распределения перетоков мощности сложной электрической сети
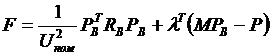 , где
, где 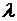 - вектор-столбец множителей Лагранжа.
- вектор-столбец множителей Лагранжа.
Для нашей сети при потоках Q, равных нулю 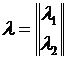 .
.
Минимум функции Лагранжа определяется системой уравнений:
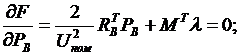

Второе уравнение - это уравнение первого закона Кирхгофа для Р, совпадающие с (2). Первое уравнение можно рассматривать как закон Ома для каждой из ветвей сети, напряжения в узлах которой равны 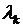 . Покажем, что эти уравнения эквивалентны уравнениям узловых напряжений.
. Покажем, что эти уравнения эквивалентны уравнениям узловых напряжений.
Для этого выразим из первого 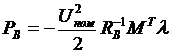 и, подставив во второе и учитывая, что
и, подставив во второе и учитывая, что  , получим
, получим  .
.
Последнее выражение перепишем так: 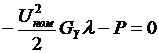 (4), где Gy — матрица активных собственных и взаимных проводимостей узлов. Примем, что напряжения узлов в сети с r равны множителям Лагранжа, умноженным на
(4), где Gy — матрица активных собственных и взаимных проводимостей узлов. Примем, что напряжения узлов в сети с r равны множителям Лагранжа, умноженным на 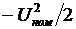 :
:  .
.
Тогда (4) — это уравнение узловых напряжений в сети только с r, для которой Gy — матрица активных узловых проводимостей, Р — вектор узловых мощностей, 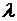 — вектор узловых напряжений, деленный на
— вектор узловых напряжений, деленный на 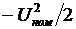 .
.
Из всего этого следует, что задача оптимизации потоков Р (3), (1) сводится к решению узловых уравнений для сложной сети с активными сопротивлениями.
Повторив подобный вывод выражений, можно получить аналогичный (4) результат для сложной сети, в которой потоки Q не равны нулю.
6.1 Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС
Рассмотрим случай чисто тепловой энергосистемы и распределение активных нагрузок между ТЭС с учетом потерь активной мощности в электрической сети. Система содержит i=1, 2, ..., п тепловых электростанций, для которых известны расходные характеристики Bi(PГ,i)и суммарная нагрузка РΣ.
Запишем:
1. Целевую функцию 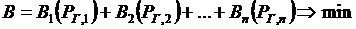 .
.
2. Уравнение связи Bi(PГ,i).
3. Ограничения 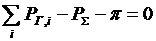 ,где
,где 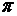 — суммарные потери активной мощности.
— суммарные потери активной мощности.
4. Функция Лагранжа  .
.
Так как выражение во второй скобке равно нулю, то минимумы функции Лагранжа и целевой функции совпадают.
Дифференцируем функцию Лагранжа по переменным 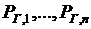 и приравниваем производные к нулю, тогда
и приравниваем производные к нулю, тогда
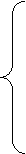
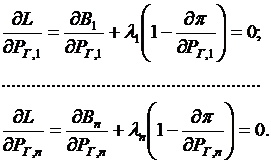 Отсюда
Отсюда 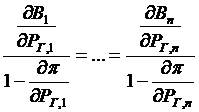
Обозначим 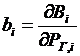 — относительный прирост расхода топлива электростанции показывает, как изменится расход топлива i-й станции, если се нагрузка изменится на величину
— относительный прирост расхода топлива электростанции показывает, как изменится расход топлива i-й станции, если се нагрузка изменится на величину 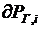 ,
,  – относительный прирост потерь активной мощности в сетях, т. е. величина, показывающая, насколько изменятся потери в сетях, если мощность только i-й станции изменится на
– относительный прирост потерь активной мощности в сетях, т. е. величина, показывающая, насколько изменятся потери в сетях, если мощность только i-й станции изменится на 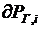 .
.
Применяя эти обозначения, получаем условия наивыгоднейшего распределения нагрузки: 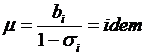 .
.
6.2 Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС
При выполнении этого условия минимум функции Лагранжа будет только в том случае, если 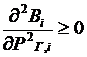 или
или 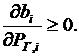 Этоозначает, что характеристики относительныхприростов электростанций должны быть монотонно возрастающими.
Этоозначает, что характеристики относительныхприростов электростанций должны быть монотонно возрастающими.
Энергетические характеристики электростанций и агрегатов чаще всего не удовлетворяют указанным требованиям. В этом случае они подлежат «исправлению» по специальной методике.
При неучете потерь активной мощности, т. е. при π = 0, условие наивыгоднейшего распределения нагрузки имеет вид: 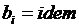 .
.
Запишем условия наивыгоднейшего распределения нагрузки в коночных разностях и умножим числители и знаменатель на ΔРг., т. е.
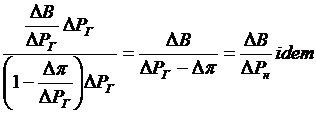 , где
, где 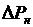 – активная мощность, доведенная до потребителя.
– активная мощность, доведенная до потребителя.
При наивыгоднейшем распределении нагрузки затраты топлива 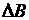 на мощность
на мощность 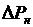 в месте ее потребления должны быть равными для всех электростанций.
в месте ее потребления должны быть равными для всех электростанций.
7.1 Определение оптимального распределения нагрузки методом множителей Лагранжа. Структурная схема алгоритма
Рассмотрим случай чисто тепловой энергосистемы и распределение активных нагрузок между ТЭС с учетом потерь активной мощности в электрической сети. Система содержит i=1, 2, ..., п тепловых электростанций, для которых известны расходные характеристики Bi(PГ,i)и суммарная нагрузка РΣ. Запишем:
5. Целевую функцию 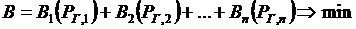 .
.
6. Уравнение связи Bi (PГ,i).
7. Ограничения 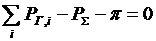 , где
, где 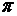 - суммарные потери P.
- суммарные потери P.
8. Функция Лагранжа  .
.
Так как выражение во второй скобке равно нулю, то минимумы функции Лагранжа и целевой функции совпадают.
Дифференцируем функцию Лагранжа по переменным 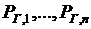 и приравниваем производные к нулю, тогда
и приравниваем производные к нулю, тогда
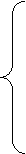
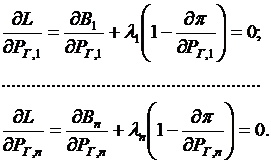 Отсюда
Отсюда 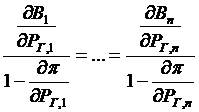
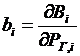 - относительный прирост расхода топлива электростанции показывает, как изменится расход топлива i-й станции, если ее нагрузка изменится на величину
- относительный прирост расхода топлива электростанции показывает, как изменится расход топлива i-й станции, если ее нагрузка изменится на величину 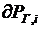 ,
,  – относительный прирост потерь Р в сетях, т. е. величина, показывающая, насколько изменятся потери в сетях, если мощность только i-й станции изменится на
– относительный прирост потерь Р в сетях, т. е. величина, показывающая, насколько изменятся потери в сетях, если мощность только i-й станции изменится на 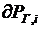 . Отсюда условия наивыгоднейшего распределения нагрузки:
. Отсюда условия наивыгоднейшего распределения нагрузки: 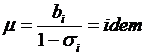 .
.
При выполнении этого условия минимум функции Лагранжа будет только в том случае, если 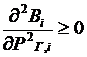 или
или 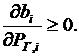
Рассмотрим алгоритм решения данной задачи.
Блоки 1—3.Находится произвольное распределение нагрузки между
7.2 Определение оптимального распределения нагрузки методом множителей Лагранжа. Структурная схема алгоритма
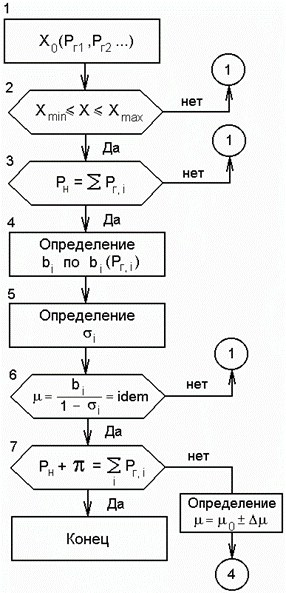 электростанциями системы
электростанциями системы 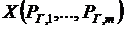 . При этом соблюдаются ограничения (блок 2) и баланс активной мощности (блок 5) без учета потерь в сетях.
. При этом соблюдаются ограничения (блок 2) и баланс активной мощности (блок 5) без учета потерь в сетях.
Блок 4.Для мощностей X находятся относительные приросты bi. Поскольку режим станции задан произвольно, то bi≠idem.
Блок 5. Для известных мощностей X определяются относительные приросты потерь активной мощности ей, что связано с расчетом режима электрической системы.
Блок 6.Изменением величины X достигается выполнение условия оптимальности 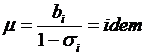 с соблюдением ограничений по допустимой мощности станции.
с соблюдением ограничений по допустимой мощности станции.
Если нарушаются ограничения  , то мощность соответствующей станции приравнивается граничному значению и считается вынужденной. Оптимизация режима осуществляется только для тех генераторных узлов, для которых соблюдаются ограничения.
, то мощность соответствующей станции приравнивается граничному значению и считается вынужденной. Оптимизация режима осуществляется только для тех генераторных узлов, для которых соблюдаются ограничения.
Блок 7. Проверяется баланс мощностей системы. Если при 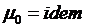 имеем
имеем 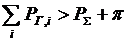 , то находится новый относительный прирост системы
, то находится новый относительный прирост системы 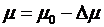 . Если
. Если  , то
, то 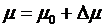 . В блоке 4 определяется новый режим активной мощности при
. В блоке 4 определяется новый режим активной мощности при 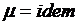 . Расчеты выполняются до тех пор, пока не будет выполняться ограничения
. Расчеты выполняются до тех пор, пока не будет выполняться ограничения 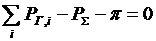 .
.
При выполнении этого ограничения и условия наивыгоднейшего распределения расчеты начинаются с блока 5 исвязаны с уточнением  и последующих расчетов. Режим будет оптимальным, если
и последующих расчетов. Режим будет оптимальным, если 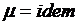 по условию наивыгоднейшего распределения, а условие
по условию наивыгоднейшего распределения, а условие 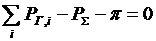 выполняется.
выполняется.
8 Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь активной мощности. Физический смысл равенства относительных приростов
Задача наивыгоднейшего распределения нагрузки без учета потерь активной мощности более характерна для распределения нагрузки между агрегатами электростанции, чем для энергосистемы. Однако для энергосистем с высокой степенью концентрации мощности такая постановка также возможна, так как неучет потерь мощности в сетях не приводит к большим погрешностям.
Поскольку π = 0, то и  = 0 и уравнение оптимизации имеет вид
= 0 и уравнение оптимизации имеет вид 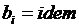 , т. е. b1 = b2 =…= bn. Оптимальный режим соответствует равенству относительных приростов станций.
, т. е. b1 = b2 =…= bn. Оптимальный режим соответствует равенству относительных приростов станций.
 Условие
Условие 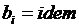 сохраняется для гидроагрегатов, турбин и котлов ТЭС. Для группы параллельно работающих агрегатов также необходимо получить равенство относительных приростов, и это даст минимум целевой функции.
сохраняется для гидроагрегатов, турбин и котлов ТЭС. Для группы параллельно работающих агрегатов также необходимо получить равенство относительных приростов, и это даст минимум целевой функции.
Принцип равенства относительных приростов объясним физически. Если относительные приросты двух работающих агрегатов, имеющих мощности Р1и Р2 и возрастающие характеристики  , не равны, то лучший режим будет у агрегата 1 с меньшим относительным приростом. Поскольку этот агрегат экономичнее другого, то его нужно загрузить дополнительно на ΔР, соответственно на ΔР снизить нагрузку другого. При этом будет получена экономия. Но при загрузке агрегата 1 на ΔР повышается его относительный прирост до
, не равны, то лучший режим будет у агрегата 1 с меньшим относительным приростом. Поскольку этот агрегат экономичнее другого, то его нужно загрузить дополнительно на ΔР, соответственно на ΔР снизить нагрузку другого. При этом будет получена экономия. Но при загрузке агрегата 1 на ΔР повышается его относительный прирост до  , а у агрегата 2 он снижается до
, а у агрегата 2 он снижается до  . Только при равенстве относительных приростов (нагрузки
. Только при равенстве относительных приростов (нагрузки 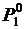 ,
, 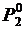 ) дальнейшее перераспределение нагрузки не дает дополнительной экономии и этот режим, следовательно, оптимальный.
) дальнейшее перераспределение нагрузки не дает дополнительной экономии и этот режим, следовательно, оптимальный.
9.1 Определение оптимального распределение нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа
Для гидротепловой энергосистемы задача наивыгоднейшего распределения нагрузки делится на две различные задачи.
Первая – оптимизация длительных режимов системы. В этой задаче для всего цикла регулирования ГЭС находится наивыгоднейшее распределение нагрузки между станциями системы и определяется режим использования водноэнергетических ресурсов водохранилищ.
Вторая – оптимизация краткосрочных режимов, или наивыгоднейшее распределение нагрузки в смешанной системе для суточного или меньшего периода оптимизации.
Распределение нагрузки при постоянстве напора ГЭС.
Пусть в системе имеется одна эквивалентная ТЭС и j ГЭС. Каждая ГЭС за период Т может израсходовать опред. кол-во энергоресурса. Задача –получить наивыгоднейшее распределение нагрузки между станциями.
1. Уравнение цели:  .
.
Расход топлива эквивалентной ТЭС Bt зависит от того, с какой мощностью она будет работать в каждом интервале времени t = l, 2, ..., k.
2. Уравнения связи – расходная энергетическая хар-ка эквивалентной ТЭС В(Ртэс) и расходные энергетические хар-ки каждой ГЭС Qj(Pj, Hj).
3. Уравнения ограничений. Для каждого интервала имеется балансовое уравнение мощностей: 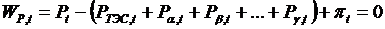 . Для каждой ГЭС задается ограничение по стоку:
. Для каждой ГЭС задается ограничение по стоку: 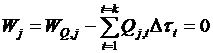 , где Pt = Pl, P2 ... - нагрузка системы в интервале t = 1, 2, ..., k; РТЭС,t - мощность ТЭС;
, где Pt = Pl, P2 ... - нагрузка системы в интервале t = 1, 2, ..., k; РТЭС,t - мощность ТЭС;  - мощности ГЭС;
- мощности ГЭС; 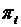 – потери P;
– потери P;  - заданные ограничения стока;
- заданные ограничения стока; 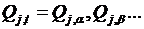 - расход ГЭС в каждом интервале длительностью
- расход ГЭС в каждом интервале длительностью  .
.
4. Уравнение оптимизации: 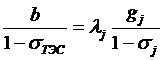 , где
, где 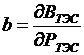 – относит. прирост расхода топлива ТЭС;
– относит. прирост расхода топлива ТЭС; 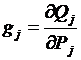 – относит, прирост расхода воды j-й ГЭС;
– относит, прирост расхода воды j-й ГЭС; 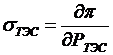 ,
, 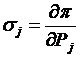 – относит, приросты потерь P при изменении мощностей ТЭС и ГЭС.
– относит, приросты потерь P при изменении мощностей ТЭС и ГЭС.
Функция Лагранжа: 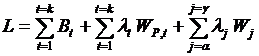 .
.
9.2 Определение оптимального распределение нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа
Неизвестными величинами будут мощности ТЭС и каждой j-й ГЭС в каждом t-м интервале времени. Неизвестны также множители Лагранжа: 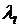 и
и 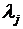 . Общее число неизвестных jt+2t+j.Чтобы решить задачу, необходимо составить jt+2t+j уравнений. Если дифференцировать ф-ю Лагранжа по независ. переменным, получим jt+tур-ий. Частные производные от ф-и Лагранжа берутся по мощностям
. Общее число неизвестных jt+2t+j.Чтобы решить задачу, необходимо составить jt+2t+j уравнений. Если дифференцировать ф-ю Лагранжа по независ. переменным, получим jt+tур-ий. Частные производные от ф-и Лагранжа берутся по мощностям 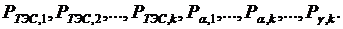
При решении этих ур-ий м. определить jt+tнеизвестных. Балансовые ур-ия стока дают j ур-ий, а балансовые ур-ия мощности — t ур-ий. Т. о, число ур-ий достаточно для определения неизвестных.
Производные по мощности ТЭС имеют вид:
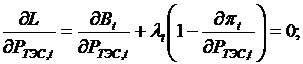
 (*)
(*)

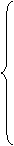
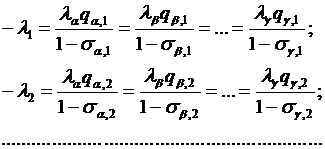 Производные по мощности ГЭС дают уравнения:
Производные по мощности ГЭС дают уравнения: 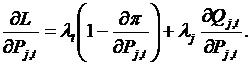 Отсюда получим:
Отсюда получим:
Из этой системы и уравнений (*) получаем условия оптимизации:

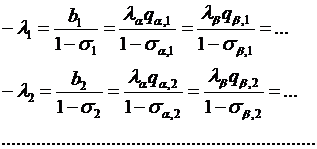 Индексы времени м. опустить и получим окончательный вид уравнения оптимизации:
Индексы времени м. опустить и получим окончательный вид уравнения оптимизации: 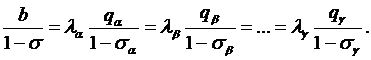
Это условие означает, что для наивыгоднейшего распред-ия нагрузки необходимо для всего периода оптимизации соблюдать постоянное соотношение 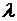 между ТЭС и ГЭС. Между ТЭС и ГЭС α нагрузка должна распределяйся по соотношению
между ТЭС и ГЭС. Между ТЭС и ГЭС α нагрузка должна распределяйся по соотношению 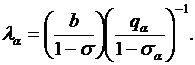 Аналогично для ГЭС β. Одновременно требуется выполнить
Аналогично для ГЭС β. Одновременно требуется выполнить 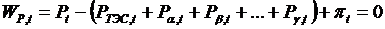 . Величины
. Величины 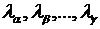 связывают режим ТЭС и соответствующей ГЭС. ГЭС могут различаться своим напором и расходом, поэтому для каждой ГЭС имеется свой
связывают режим ТЭС и соответствующей ГЭС. ГЭС могут различаться своим напором и расходом, поэтому для каждой ГЭС имеется свой 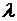 .
.
10.1 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме
Рассмотрим систему, состоящую из одной ТЭС и одной ГЭС. Условие наивыгоднейшего распределения нагрузки в такой системе имеет вид: b = λq.
Известно, что 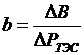 ,
, 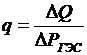 , тогда
, тогда 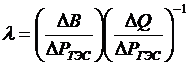 .
.
Будем рассматривать равные приращения мощности на электростанциях, т. е.  , тогда
, тогда 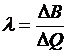 .
.
Следовательно, 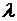 – мера эффективности использования гидроресурсов в системе. Этот коэффициент показывает, какая экономия топлива будет получена на тепловой станции, если на ГЭС будет использован расход
– мера эффективности использования гидроресурсов в системе. Этот коэффициент показывает, какая экономия топлива будет получена на тепловой станции, если на ГЭС будет использован расход  . Естественно, что наивыгоднейшим будет такой режим, при котором ресурсы каждой ГЭС будут использованы с одинаковой эффективностью в течение всего периода оптимизации. Таким образом, в течение всего периода оптимизации наивыгоднейшее распределение будет при
. Естественно, что наивыгоднейшим будет такой режим, при котором ресурсы каждой ГЭС будут использованы с одинаковой эффективностью в течение всего периода оптимизации. Таким образом, в течение всего периода оптимизации наивыгоднейшее распределение будет при 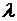 = idem.
= idem.
 Коэффициент λ связан с параметрами ГЭС, т. е. с ее расходом и напором, так как энергия расхода
Коэффициент λ связан с параметрами ГЭС, т. е. с ее расходом и напором, так как энергия расхода  зависит от напора ГЭС. Рассмотрим вначале его связь с расходом при условии постоянства напора H = const. Пусть между станциями распределена нагрузка системы Р, причем
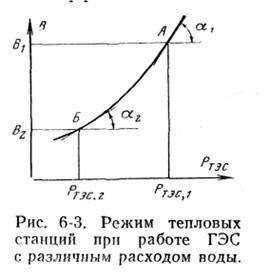
зависит от напора ГЭС. Рассмотрим вначале его связь с расходом при условии постоянства напора H = const. Пусть между станциями распределена нагрузка системы Р, причем 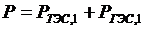 . При таком распределении тепловая станция имеет расход топлива В1 (рис. 6-3), а относительный прирост расхода топлива в точке А равен
. При таком распределении тепловая станция имеет расход топлива В1 (рис. 6-3), а относительный прирост расхода топлива в точке А равен 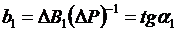 . Эффективность использования стока
. Эффективность использования стока 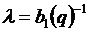 .
.
Рассмотрим теперь такой баланс мощности, когда ГЭС работает с большей мощностью 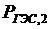 т. е.
т. е.  . Естественно, при мощности
. Естественно, при мощности 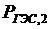 расход воды возрастает и
расход воды возрастает и 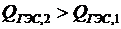 . Тепловая станция имеет расход В2 (точка Б) и относительный прирост
. Тепловая станция имеет расход В2 (точка Б) и относительный прирост 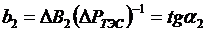 . Видно, что b2 < b1 и λ2 < λ1. Отсюда эффективность использования гидроресурсов в системе обратно пропорциональна расходу ГЭС. Действительно, если ГЭС работает с малыми расходом и мощностью, то в системе работают и неэкономичные тепловые станции. Каждый дополнительный кубометр воды ГЭС будет давать
. Видно, что b2 < b1 и λ2 < λ1. Отсюда эффективность использования гидроресурсов в системе обратно пропорциональна расходу ГЭС. Действительно, если ГЭС работает с малыми расходом и мощностью, то в системе работают и неэкономичные тепловые станции. Каждый дополнительный кубометр воды ГЭС будет давать
 10.2 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме
10.2 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме
экономию топлива за счет разгрузки неэкономичного оборудования. Если же ГЭС работает с большими расходами и мощностью, то на тепловых станциях используется более экономичное оборудование, а следовательно, происходит уменьшение λ.
 В данной задаче заданы ограничения стока ГЭС. Коэффициент λ должен соответствовать заданному стоку (рис. 6-4). Эта задача решается подбором.
В данной задаче заданы ограничения стока ГЭС. Коэффициент λ должен соответствовать заданному стоку (рис. 6-4). Эта задача решается подбором.
Коэффициент λ прямо пропорционально связан с напором ГЭС. Действительно, если ГЭС работает с постоянной мощностью 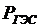 , а напоры ее Н1 и Н2 различны, то при Н1 > Н2 Q1 < Q2 (рис. 6.5).
, а напоры ее Н1 и Н2 различны, то при Н1 > Н2 Q1 < Q2 (рис. 6.5).
11.1 Опт. распред-ие нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения
Пусть в системе имеется одна эквивалентная ТЭС и j ГЭС. Каждая ГЭС за период Т может израсходовать опред. кол-во энергоресурса. Задача –получить наивыгоднейшее распределение нагрузки между станциями.
5. Уравнение цели:  .
.
Расход топлива эквивалентной ТЭС Bt зависит от того, с какой мощностью она будет работать в каждом интервале времени t = l, 2, ..., k.
6. Уравнения связи – расходная энергетическая хар-ка эквивалентной ТЭС В(Ртэс) и расходные энергетические хар-ки каждой ГЭС Qj(Pj, Hj).
7. Уравнения ограничений. Для каждого интервала имеется балансовое уравнение мощностей: 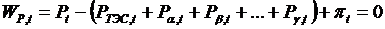 . Для каждой ГЭС задается ограничение по стоку:
. Для каждой ГЭС задается ограничение по стоку: 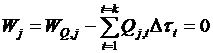 , где Pt = Pl, P2 ... - нагрузка системы в интервале t = 1, 2, ..., k; РТЭС,t - мощность ТЭС;
, где Pt = Pl, P2 ... - нагрузка системы в интервале t = 1, 2, ..., k; РТЭС,t - мощность ТЭС;  - мощности ГЭС;
- мощности ГЭС; 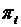 – потери P;
– потери P;  - заданные ограничения стока;
- заданные ограничения стока; 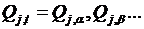 - расход ГЭС в каждом интервале длительностью
- расход ГЭС в каждом интервале длительностью  .
.
8. Уравнение оптимизации: 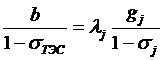 , где
, где 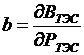 – относит. прирост расхода топлива ТЭС;
– относит. прирост расхода топлива ТЭС; 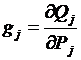 – относит, прирост расхода воды j-й ГЭС;
– относит, прирост расхода воды j-й ГЭС; 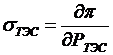 ,
, 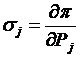 – относит, приросты потерь P при изменении мощностей ТЭС и ГЭС.
– относит, приросты потерь P при изменении мощностей ТЭС и ГЭС.
Функция Лагранжа: 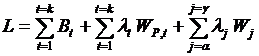 .
.
Неизвестными величинами будут мощности ТЭС и каждой j-й ГЭС в каждом t-м интервале времени. Неизвестны также множители Лагранжа: 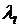 и
и 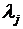 . Общее число неизвестных jt+2t+j.Чтобы решить задачу, необходимо составить jt+2t+j уравнений. Если дифференцировать ф-ю Лагранжа по независ. переменным, получим jt+tур-ий. Частные производные от ф-и Лагранжа берутся по мощностям
. Общее число неизвестных jt+2t+j.Чтобы решить задачу, необходимо составить jt+2t+j уравнений. Если дифференцировать ф-ю Лагранжа по независ. переменным, получим jt+tур-ий. Частные производные от ф-и Лагранжа берутся по мощностям 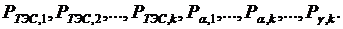
При решении этих ур-ий м. определить jt+tнеизвестных. Балансовые ур-ия стока дают j ур-ий, а балансовые ур-ия мощности — t ур-ий. Т. о, число ур-ий достаточно для определения неизвестных.
11.2 Опт. распред-ие нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения
Производные по мощности ТЭС имеют вид:
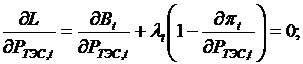
 (*)
(*)
Производные по мощности ГЭС дают уравнения: 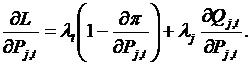 Отсюда получим:
Отсюда получим:

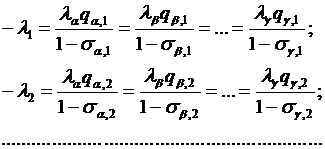
Из этой системы и уравнений (*) получаем условия оптимизации:

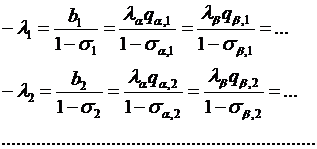 Индексы времени м. опустить и получим окончательный вид уравнения оптимизации:
Индексы времени м. опустить и получим окончательный вид уравнения оптимизации: 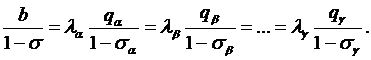
Это условие означает, что для наивыгоднейшего распред-ия нагрузки необходимо для всего периода оптимизации соблюдать постоянное соотношение 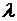 между ТЭС и ГЭС. Между ТЭС и ГЭС α нагрузка должна распределяйся по соотношению
между ТЭС и ГЭС. Между ТЭС и ГЭС α нагрузка должна распределяйся по соотношению 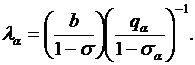 Аналогично для ГЭС β. Одновременно требуется выполнить
Аналогично для ГЭС β. Одновременно требуется выполнить 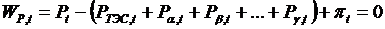 . Величины
. Величины 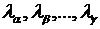 связывают режим ТЭС и соответствующей ГЭС. ГЭС могут различаться своим напором и расходом, поэтому для каждой ГЭС имеется свой
связывают режим ТЭС и соответствующей ГЭС. ГЭС могут различаться своим напором и расходом, поэтому для каждой ГЭС имеется свой 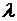 .
.
Блоки 1—3. Задается нагрузка ГЭС РГЭС,1 для t = l и проверяется ее допустимость. Если мощности ГЭС не удовлетворяют ограничениям, то они корректируются с приращением ± ΔP.
Блоки 4 и 5. Из уравнения баланса определяется мощность ТЭС и проверяется ее допустимость. Если она недопустима, то корректируется мощность ГЭС и расчет возвращается в 2.
11.3 Опт. распред-ие нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения
 Блок 6. Производится расчет режима сети и относительных приростов потерь.
Блок 6. Производится расчет режима сети и относительных приростов потерь.
Блоки 7 и 8. Для исходного произвольного и в общем случае неоптимального распределения нагрузки находятся относительные приросты станций с учетом σ. Такие расчеты проводятся для всех интервалов времени t = l, 2, ... k.
Блоки 9 и 10. Для каждого t подсчитываются коэффициенты λt. Так как распределение нагрузки было произвольным, то нет постоянства λ для периода оптимизации, т. е. режим не является оптимальным. Уравнивание λ производится по отношению к среднему значению λср.
Блоки 11 и 12. Уравнивание λt и λср производится в зависимости от знака разности Δλ=λср—λt приращением мощности ±ΔР. Расчеты каждый раз начинаются с блока 2. При выполнении условия блока 12 режим является допустимым и λ = idem, но он еще может быть неоптимальным, так как не проверено ограничение по стоку.
Блоки 13 и 14. Если сток ГЭС WГЭС равен заданному W3ад, то задача решена, если же WГЭС ≠ Wзад, то в зависимости от знака небаланса ΔW = Wзад — Wгэс меняется мощность ГЭС с шагом ±ΔР и расчет снова начинается с 2.
 12.1 Оптимальное распределение нагрузки при переменном напоре ГЭС
12.1 Оптимальное распределение нагрузки при переменном напоре ГЭС
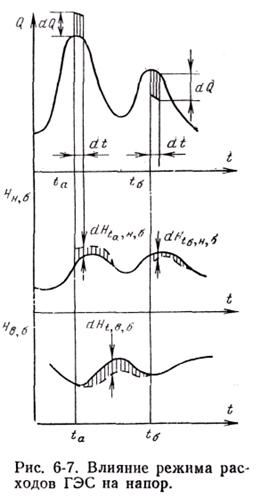
Пусть в системе имеется две станции – гидравлическая и тепловая. Между ними произвольно распределен заданный график нагрузки с соблюдением баланса мощности. По графику мощностей ГЭС определен график ее расходов (рис. 6-7).
Перераспределим нагрузку и посмотрим, к каким изменениям в системе это может привести. В момент ta на интервале dt увеличим расход ГЭС на величину dQ, а в дальнейшем в момент tб на интервале dt уменьшим расход ГЭС на ту же величину dQ. Как изменятся мощности станций в период от ta до tб? Увеличение расхода приведет к увеличению мощности на 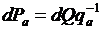 и к такому же снижению мощности тепловой станции.
и к такому же снижению мощности тепловой станции.
Тепловая станция системы будет иметь экономию топлива 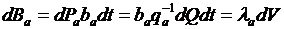 , где qa, ba – относительные приросты ГЭС и ТЭС;
, где qa, ba – относительные приросты ГЭС и ТЭС; 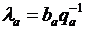 – множитель Лагранжа; dV = dQdt — дополнительный сток ГЭС.
– множитель Лагранжа; dV = dQdt — дополнительный сток ГЭС.
Величина экономии топлива найдена без учета изменчивости напора. В действительности увеличение расхода приводит к увеличению уровня нижнего бьефа. Так как этот процесс затухает медленно, то он будет продолжаться от ta до бесконечности. Мощность ГЭС при этом снижается на 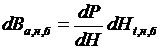 . Поэтому, чтобы судить о мощностях, нужно знать изменчивость уровней нижнего бьефа
. Поэтому, чтобы судить о мощностях, нужно знать изменчивость уровней нижнего бьефа 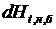 .
.
Дополнительный расход топлива ТЭС за счет увеличения уровня нижнего бьефа на 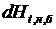 будет равен:
будет равен:  , где принято обозначение
, где принято обозначение 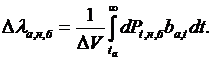 Такое обозначение введено потому, что величина
Такое обозначение введено потому, что величина 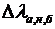 имеет ту же размерность, что и коэффициент эффективности
имеет ту же размерность, что и коэффициент эффективности 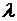 . Подобные рассуждения можно применить к моменту tб, когда будет восстановлен баланс стока ГЭС, тогда получим:
. Подобные рассуждения можно применить к моменту tб, когда будет восстановлен баланс стока ГЭС, тогда получим: 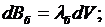

12.2 Оптимальное распределение нагрузки при переменном напоре ГЭС
Но напор меняется и за счет изменчивости верхнего бьефа, поэтому необходимо учесть эффект последействия. В течение периода от ta до tб ГЭС работает с пониженными на 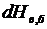 по сравнению с первоначальным режимом уровнями верхнего бьефа.
по сравнению с первоначальным режимом уровнями верхнего бьефа.
Можно так определить снижение мощности ГЭС в этот период: 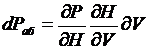 , причем производная
, причем производная 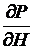 показывает изменение мощности ГЭС от напора, а
показывает изменение мощности ГЭС от напора, а 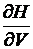 – изменение напора от объема. Всего же объем изменился на dV. Пережог топлива на ТЭС
– изменение напора от объема. Всего же объем изменился на dV. Пережог топлива на ТЭС  , причем размерность этой величины также совпадает с размерностью коэффициента эффективности
, причем размерность этой величины также совпадает с размерностью коэффициента эффективности 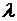 .
.
Общее изменение расхода топлива системы равно: 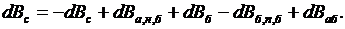
Если первоначальное распределение нагрузки было лучше второго, то 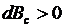 ; если же последующий режим лучше, то
; если же последующий режим лучше, то 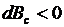 , т. е. в системе будет экономия топлива. Примем для дальнейшего условие равноэкономичности режимов за расчетное, что соответствует
, т. е. в системе будет экономия топлива. Примем для дальнейшего условие равноэкономичности режимов за расчетное, что соответствует 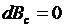 . Из последнего выражения после сокращения dV следует:
. Из последнего выражения после сокращения dV следует: 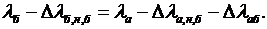 Отсюда следует, что при непостоянстве напора ГЭС значение λ, не остается постоянным, как при постоянстве напоров. Поэтому на каждом расчетном интервале времени требуется определять свой λ.
Отсюда следует, что при непостоянстве напора ГЭС значение λ, не остается постоянным, как при постоянстве напоров. Поэтому на каждом расчетном интервале времени требуется определять свой λ.
13.1 Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения агрегатов электростанций
Используя метод неопределенных множителей Лагранжа, м. получить условие наивыгоднейшего распределения нагрузки между агрегатами электростанции в виде равенства отношения приращения первичного ресурса (подведенной мощности) к приращению вторичного (полезной мощности).
Распределение нагрузки между агрегатами ТЭС. Для ТЭС возникают задачи распределения нагрузки между турбинами, котлами, блоками, частями станции. Условия наивыгоднейшего распределения нагрузки:
 между конденсационными турбинами
между конденсационными турбинами  между котлами
между котлами  между блоками
между блоками 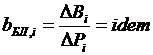 , где
, где 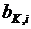 – относительный прирост котла, показывающий изменение расхода условного топлива котла
– относительный прирост котла, показывающий изменение расхода условного топлива котла 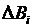 при изменении паросъема на
при изменении паросъема на  ;
; 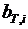 – относительный прирост турбины, показывающий изменение расхода пара
– относительный прирост турбины, показывающий изменение расхода пара  при изменении мощности турбин на
при изменении мощности турбин на 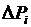 ;
; 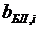 – относительный прирост блока.
– относительный прирост блока.
На практике на эти условия могут накладываться ограничения, определяемые видом характеристики, которые могут иметь скачки, участки с постоянными относительными приростами и т. п.
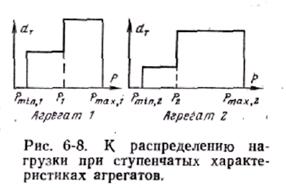
Если нагрузка распределяется между агрегатами, которые имеют ступенчато - кусочные характеристики (рис. 6,8), то они загружаются в порядке возрастания их относительных приростов. Например, при росте нагрузки от минимальной 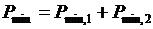 в начале загружается агрегат 2, т. к. он имеет меньший относительный прирост. Если нагрузка превышает
в начале загружается агрегат 2, т. к. он имеет меньший относительный прирост. Если нагрузка превышает 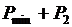 , то загружается агрегат 1. При нагрузке большей
, то загружается агрегат 1. При нагрузке большей 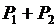 снова загружается агрегат 2, а при
снова загружается агрегат 2, а при  – агрегат 1. При этом сохраняется принцип использования тех агрегатов, которые дают большую экономию топлива. Т. о, если агрегаты не имеют равных относительных приростов, то они загружаются в порядке возрастания относительных приростов.
– агрегат 1. При этом сохраняется принцип использования тех агрегатов, которые дают большую экономию топлива. Т. о, если агрегаты не имеют равных относительных приростов, то они загружаются в порядке возрастания относительных приростов.
Для станций, имеющих теплофикационные турбины относительные приросты зависят также и от расхода пара, идущего в производственные отборы 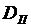 . При распределении нагрузки между турбинами с отборами условия наивыгоднейшего распределения нагрузки имеют вид:
. При распределении нагрузки между турбинами с отборами условия наивыгоднейшего распределения нагрузки имеют вид:
13.2 Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения
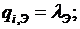 агрегатов электростанций
агрегатов электростанций
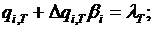
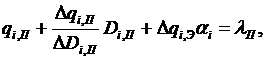 где
где 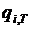 ,
, 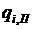 – относительные приросты расхода тепла при изменении величины отбора и постоянстве электрической мощности;
– относительные приросты расхода тепла при изменении величины отбора и постоянстве электрической мощности;  – относительный прирост расхода тепла при изменении электрической мощности.
– относительный прирост расхода тепла при изменении электрической мощности.
Распределение нагрузки между агрегатами ГЭС. Для ГЭС наивыгоднейшее распределение нагрузки будет в том случае, когда агрегаты работают с равными относительными приростами: 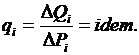
Из условий наивыгоднейшего распределения нагрузки следует, что методика решения задачи о наивыгоднейшем распределении нагрузки между агрегатами электростанций проста, если известны их характеристики относительных приростов.
 В условиях эксплуатации желательно было бы при распределении нагрузки между агрегатами использовать не характеристики, а текущие измерения относительных приростов. Для ГЭС, чтобы получить относительный прирост агрегата, нужно измерить расходы Q1 и Q2 и мощности Р1 и Р2 с малым шагом дискретности, т. е. получить
В условиях эксплуатации желательно было бы при распределении нагрузки между агрегатами использовать не характеристики, а текущие измерения относительных приростов. Для ГЭС, чтобы получить относительный прирост агрегата, нужно измерить расходы Q1 и Q2 и мощности Р1 и Р2 с малым шагом дискретности, т. е. получить 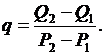
Этот дифференциальный показатель очень чувствителен к погрешностям измерения расходов и мощностей, может резко меняться, поэтому измеренные характеристики относительных приростов обычно не являются выпуклыми, не удовлетворяют требованиям метода неопределенных множителей Лагранжа и точность их низка.
На рис. 6-9 показаны характеристики относительных приростов различных гидроагрегатов, полученные при натурных испытаниях. Прежде чем воспользоваться такими характеристиками, нужно их обработать. Некачественность хар-к приводит к снижению эффекта оптимального распределения нагрузки между агрегатами.
14.1 Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования. Основные определения
Как известно, общая задача нелинейного программирования заключается в отыскании экстремума целевой функции F при заданных ограничениях в виде равенств и неравенств. При этом в качестве целевой функции выступает суммарный расход топлива в энергосистеме В.
Расход В есть функция независимых и зависимых переменных. Обозначим через 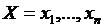 вектор независимых переменных; через
вектор независимых переменных; через  вектор зависимых переменных. К независимым переменным относятся активные и реактивные мощности станций. К числу зависимых переменных относятся напряжения генерирующих узлов нагрузочных узлов. Следовательно, задача оптимизации сводится к отысканию экстремума
вектор зависимых переменных. К независимым переменным относятся активные и реактивные мощности станций. К числу зависимых переменных относятся напряжения генерирующих узлов нагрузочных узлов. Следовательно, задача оптимизации сводится к отысканию экстремума  с учетом уравнении связи между зависимыми и независимыми переменными
с учетом уравнении связи между зависимыми и независимыми переменными 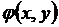 которые часто рассматриваются как ограничения в форме равенств. В качестве уравнений связи используются уравнения, описывающие установившийся режим электрической системы, например уравнения узловых напряжений. Т. к. УУН являются нелинейными, отыскание зависимых переменных связано с задачей расчета режима электрической системы посредством решения УУН.
которые часто рассматриваются как ограничения в форме равенств. В качестве уравнений связи используются уравнения, описывающие установившийся режим электрической системы, например уравнения узловых напряжений. Т. к. УУН являются нелинейными, отыскание зависимых переменных связано с задачей расчета режима электрической системы посредством решения УУН.
Целевая функция выглядит следующим образом:
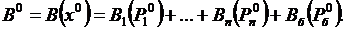
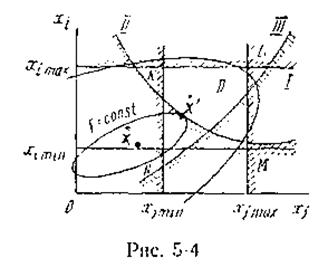 Оптимальный режим должен удовлетворять системе режимных ограничений в виде неравенств:
Оптимальный режим должен удовлетворять системе режимных ограничений в виде неравенств:
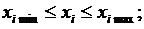
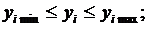 (*)
(*)
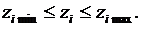
Линия (поверхность) равного уровня целевой функции — геометрическое место точек в пространстве независимых переменных  , в которых целевая функция имеет одно и то же значение F = const. На рис. 5-4 показаны проекции линий равного уровня на плоскость
, в которых целевая функция имеет одно и то же значение F = const. На рис. 5-4 показаны проекции линий равного уровня на плоскость  ,
,  . Каждая из систем неравенств (*) определяет некоторую допустимую область Dx, Dy, Dz. Результирующая область допустимых нормальных режимов D, удовлетворяющих всем перечисленным ограничениям, определяется пересечением этих областей.
. Каждая из систем неравенств (*) определяет некоторую допустимую область Dx, Dy, Dz. Результирующая область допустимых нормальных режимов D, удовлетворяющих всем перечисленным ограничениям, определяется пересечением этих областей.
14.2 Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования. Основные определения
Область выпукла, если для любой пары точек данной области отрезок прямой линии, соединяющей эти точки, также полностью принадлежит этой области.
Абсолютным минимумом называется точка экстремума целевой функции без учета ограничений ( 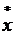 на рис. 5-4).
на рис. 5-4).
Относительным экстремумом называется точка 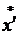 на границе области, где целевая функция принимает минимальное значение внутри области. Точка
на границе области, где целевая функция принимает минимальное значение внутри области. Точка 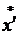 и соответствующее ей значение целевой функции называются оптимальным решением задачи. Если целевая функция унимодальна (имеет один экстремум), т. е. в любой точке
и соответствующее ей значение целевой функции называются оптимальным решением задачи. Если целевая функция унимодальна (имеет один экстремум), т. е. в любой точке 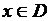 значение
значение 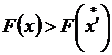 , то оптимальное решение является глобальным. Если функция мультимодальна (многоэкстремальна), то найденное экстремальное решение необязательно глобальное и может быть локальным.
, то оптимальное решение является глобальным. Если функция мультимодальна (многоэкстремальна), то найденное экстремальное решение необязательно глобальное и может быть локальным.
Среди ограничений (*) можно выделить активные и пассивные. Если в точке 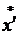 тот пли иной параметр принимает граничное значение, то соответствующее ему ограничение называется активным (ограничение II на рис. 5-4), остальные же ограничения — пассивными. Пассивные ограничения можно не учитывать в ходе оптимизации, однако заранее неизвестно, какие из ограничений являются активными, а какие — пассивными, и только поэтому приходится рассматривать всю совокупность ограничений.
тот пли иной параметр принимает граничное значение, то соответствующее ему ограничение называется активным (ограничение II на рис. 5-4), остальные же ограничения — пассивными. Пассивные ограничения можно не учитывать в ходе оптимизации, однако заранее неизвестно, какие из ограничений являются активными, а какие — пассивными, и только поэтому приходится рассматривать всю совокупность ограничений.
15.1 Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике
Методы возможных относятся к классу итеративных, т. е. методов последовательных приближений, в которых строится последовательность точек х°, х1, ..., хк, стремящихся к значению 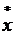 на основании следующего критерия оптимальности: каждая точка xk должна быть лучше предыдущей хk-1:
на основании следующего критерия оптимальности: каждая точка xk должна быть лучше предыдущей хk-1: 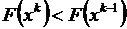 .
.
Последовательность точек хk образует траекторию спуска к минимуму F. Количество шагов в спуске, необходимое для приближения к экстремуму с заданной точностью, зависит как от выбранного исходного приближения х°, так и от способа организации спуска, т. с. перехода от х° к х1, и т. д.
 Суть методов возможных направлений заключается в том, что спуск из любой точки х° к
Суть методов возможных направлений заключается в том, что спуск из любой точки х° к 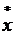 можно осуществить по различным направлениям, называемым возможными, при которых последовательно уменьшается функция F(x).
можно осуществить по различным направлениям, называемым возможными, при которых последовательно уменьшается функция F(x).
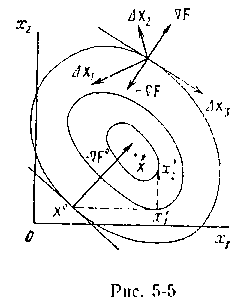
Все направления можно разбить на три типа (рис. 5-5): 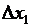 – направления, приводящие к уменьшению целевой функции;
– направления, приводящие к уменьшению целевой функции; 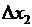 – направления, приводящие к возрастанию целевой функции (противоположные направления dir (—
– направления, приводящие к возрастанию целевой функции (противоположные направления dir (— 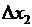 ) – также возможные направления спуска);
) – также возможные направления спуска); 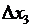 – направления, лежащие в плоскости, касательной к поверхности равного уровня Fо = const, не приводящие к уменьшению функции ни в прямом, ни в обратном направлениях. Таким образом, с учетом реверса любое направление, отличающееся от касательного, следует рассматривать как возможное.
– направления, лежащие в плоскости, касательной к поверхности равного уровня Fо = const, не приводящие к уменьшению функции ни в прямом, ни в обратном направлениях. Таким образом, с учетом реверса любое направление, отличающееся от касательного, следует рассматривать как возможное.
Вектор, ортогональный к касательной плоскости и указывающий направление наибольшей скорости возрастания функции F, называется градиентом функции F в точке х° и обозначается как  . С точки зрения локальных свойств противоположное ему направление антиградиента
. С точки зрения локальных свойств противоположное ему направление антиградиента 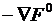 является наилучшим из всех возможных направлений, так как оно показывает путь наибольшего убывания функции F(x°).
является наилучшим из всех возможных направлений, так как оно показывает путь наибольшего убывания функции F(x°).
15.2 Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике
Критерием выбора возможного направления Δх является условие 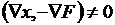 , означающее, что скалярное произведение векторов Δх и антиградиента не должно быть равно нулю, т. е. возможное направление не должно быть ортогонально антиградиенту. Если в точке xk каким-либо образом найдено возможное направление спуска Δxk, то во всех рассматриваемых методах новая точка на траектории спуска вычисляется по рекуррентному выражению
, означающее, что скалярное произведение векторов Δх и антиградиента не должно быть равно нулю, т. е. возможное направление не должно быть ортогонально антиградиенту. Если в точке xk каким-либо образом найдено возможное направление спуска Δxk, то во всех рассматриваемых методах новая точка на траектории спуска вычисляется по рекуррентному выражению 
Различия в многочисленных методах возможных направлений состоят либо в способах задания направления спуска, либо в способах определения величины qk, представляющей собой длину шага вдоль вектора 
Все методы нелинейного программирования, основанные па рекуррентном выражении (5-76), можно разделить на два класса в зависимости от способа задания длины шага: методы использования постоянного шага и методы наискорейшего спуска.
В методе наискорейшего спуска исходная величина 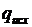 задается в виде константы. Однако для обеспечения сходимости процесса вычислений, чтобы на каждом шаге выполнялся критерий
задается в виде константы. Однако для обеспечения сходимости процесса вычислений, чтобы на каждом шаге выполнялся критерий 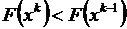 , необходим контроль правильного задания длины шага. При неудачно заданном значении
, необходим контроль правильного задания длины шага. При неудачно заданном значении 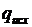 критерий может быть нарушен, т. е.
критерий может быть нарушен, т. е. 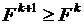 . В этом случае необходимо уменьшить длину шага, т. е. воспользоваться формулой
. В этом случае необходимо уменьшить длину шага, т. е. воспользоваться формулой 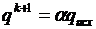 , где
, где 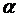 — также некоторая константа, меньшая единицы.
— также некоторая константа, меньшая единицы.
Процедура решения 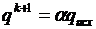 выполняется до тех пор, пока не будет выполнено условие
выполняется до тех пор, пока не будет выполнено условие 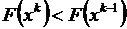 . При этом в качестве
. При этом в качестве 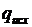 рассматривается последнее значение
рассматривается последнее значение  .
.
Достоинство методов этого класса — малый объем вычислений на шаге. Недостаток заключается в том, что при неудачно выбранных значениях 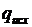 и
и 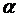 количество шагов оптимизации может быть велико и в целом объем вычислений, а следовательно, и время решения задачи могут быть недопустимо большими.
количество шагов оптимизации может быть велико и в целом объем вычислений, а следовательно, и время решения задачи могут быть недопустимо большими.
16 Применение метода наискорейшего спуска при решении задач оптимизации в электроэнергетике
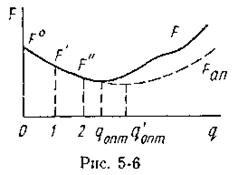 В данном методе длина шага qk зависит от направления спуска Δxk и вычисляется из условия обеспечения максимального уменьшения целевой функции в заданном направлении. Задача формулируется таким образом, чтобы найти значение
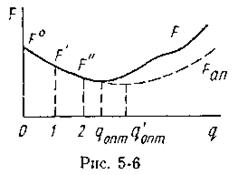
В данном методе длина шага qk зависит от направления спуска Δxk и вычисляется из условия обеспечения максимального уменьшения целевой функции в заданном направлении. Задача формулируется таким образом, чтобы найти значение  , обеспечивающее минимум F(х) на Δx. Функция F(х) изменяется в направлении Δx. Для каждой конкретной задачи и направления может быть построена зависимость F(q) = F (х° + q Δxk), имеющая один экстремум для унимодальной функции (рис. 5-6). Чтобы найти оптимальную длину шага
, обеспечивающее минимум F(х) на Δx. Функция F(х) изменяется в направлении Δx. Для каждой конкретной задачи и направления может быть построена зависимость F(q) = F (х° + q Δxk), имеющая один экстремум для унимодальной функции (рис. 5-6). Чтобы найти оптимальную длину шага  , необходимо продифференцировать аналитическую функцию F(q) и, приравняв производную нулю
, необходимо продифференцировать аналитическую функцию F(q) и, приравняв производную нулю 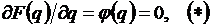 решить полученное уравнение относительно q.
решить полученное уравнение относительно q.
Определение величины  – задача одномерного поиска экстремума функции одной переменной F(q). Однако путь точного аналитического определения
– задача одномерного поиска экстремума функции одной переменной F(q). Однако путь точного аналитического определения  часто оказывается неприемлемым, так как получение зависимости F(q) может быть сопряжено с большими трудностями. Кроме того, уравнение
часто оказывается неприемлемым, так как получение зависимости F(q) может быть сопряжено с большими трудностями. Кроме того, уравнение  относительно
относительно  может быть нелинейным, а его решение — непростым. Поэтому зависимость F(q) аппроксимируют чаще всего полиномом второй степени
может быть нелинейным, а его решение — непростым. Поэтому зависимость F(q) аппроксимируют чаще всего полиномом второй степени 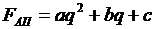 и находят псевдооптимальную длину шага
и находят псевдооптимальную длину шага  , что следует из
, что следует из 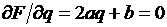 .
.
Параметры полинома a, b, c можно найти, если вычислить любые три точки, удовлетворяющие зависимости F(q). Удобно в качестве узлов аппроксимации принять значения F°, F', F" в точках х°; х' = х° + Δх; х" = х° + 2Δх, т. е. вычислить функцию соответственно в исходной точке, далее в точках х' и х" при одинарном шаге (q = 1) и двойном шаге (q = 2) вдоль вектора Δх. Подставив параметры трех узлов аппроксимации в наш полином, при q = 0, q = 1 и q = 2 получаем соответственно
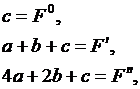
откуда 
17 Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике
 В данном методе длина шага qk зависит от направления спуска Δxk и вычисляется из условия обеспечения максимального уменьшения целевой функции в заданном направлении. Задача формулируется таким образом, чтобы найти значение
В данном методе длина шага qk зависит от направления спуска Δxk и вычисляется из условия обеспечения максимального уменьшения целевой функции в заданном направлении. Задача формулируется таким образом, чтобы найти значение  , обеспечивающее минимум F(х) на Δx. Функция F(х) изменяется в направлении Δx. Для каждой конкретной задачи и направления может быть построена зависимость F(q) = F (х° + q Δxk), имеющая один экстремум для унимодальной функции (рис. 5-6). Чтобы найти оптимальную длину шага
, обеспечивающее минимум F(х) на Δx. Функция F(х) изменяется в направлении Δx. Для каждой конкретной задачи и направления может быть построена зависимость F(q) = F (х° + q Δxk), имеющая один экстремум для унимодальной функции (рис. 5-6). Чтобы найти оптимальную длину шага  , необходимо продифференцировать аналитическую функцию F(q) и, приравняв производную нулю
, необходимо продифференцировать аналитическую функцию F(q) и, приравняв производную нулю 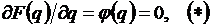 решить полученное уравнение относительно q.
решить полученное уравнение относительно q.
Определение величины  – задача одномерного поиска экстремума функции одной переменной F(q). Однако путь точного аналитического определения
– задача одномерного поиска экстремума функции одной переменной F(q). Однако путь точного аналитического определения  часто оказывается неприемлемым, так как получение зависимости F(q) может быть сопряжено с большими трудностями. Кроме того, уравнение
часто оказывается неприемлемым, так как получение зависимости F(q) может быть сопряжено с большими трудностями. Кроме того, уравнение  относительно
относительно  может быть нелинейным, а его решение — непростым. Поэтому зависимость F(q) аппроксимируют чаще всего полиномом второй степени
может быть нелинейным, а его решение — непростым. Поэтому зависимость F(q) аппроксимируют чаще всего полиномом второй степени 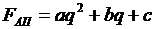 и находят псевдооптимальную длину шага
и находят псевдооптимальную длину шага  , что следует из
, что следует из 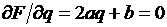 .
.
Параметры полинома a, b, c можно найти, если вычислить любые три точки, удовлетворяющие зависимости F(q). Удобно в качестве узлов аппроксимации принять значения F°, F', F" в точках х°; х' = х° + Δх; х" = х° + 2Δх, т. е. вычислить функцию соответственно в исходной точке, далее в точках х' и х" при одинарном шаге (q = 1) и двойном шаге (q = 2) вдоль вектора Δх. Подставив параметры трех узлов аппроксимации в наш полином, при q = 0, q = 1 и q = 2 получаем соответственно
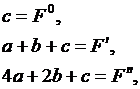
откуда 
18 Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода
 Метод покоординатной оптимизации относится к наиболее простым по реализации алгоритмам. Суть его заключается в том, что в качестве возможных направлений рассматриваются орты исходной системы координат
Метод покоординатной оптимизации относится к наиболее простым по реализации алгоритмам. Суть его заключается в том, что в качестве возможных направлений рассматриваются орты исходной системы координат 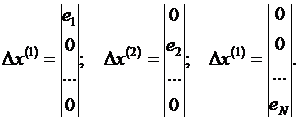
При этом N шагов по всем независимым переменным образуют внутренний цикл. Это означает, что на первом итерационном шаге минимизируется целевая функция F(x) при изменении только первой переменной, а все остальные переменные остаются неизменными. Если спуск осуществляется с отысканием оптимальной длины шага, то 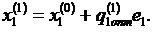
 На втором шаге процедура повторяется для второй переменной:
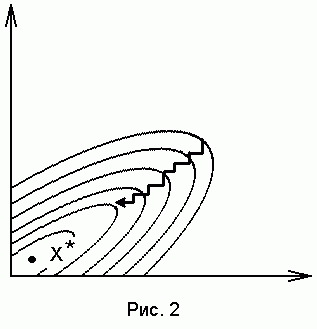
На втором шаге процедура повторяется для второй переменной: 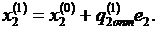 Частная минимизация по всем N переменным образует полный цикл, называемый внешним. Количество внешних циклов, т. е. повторений внутренних циклов, заранее неизвестно и определяется сходимостью вычислительного процесса, которая зависит от свойств минимизируемой функции F(x) и выбора исходного приближения х°. На рис. 1 штриховой линией показана траектория спуска. Несмотря на простоту реализации и малый объем вычислений на шаге, часто от метода приходится отказываться из-за неудовлетворительной сходимости. На рис. 2 приведена геометрическая интерпретация так называемой «овражной» функции для двумерной задачи F(x1, х2). Если «дно оврага» не совпадает с направлением координатных осей, то количество шагов становится неприемлемо большим.
Частная минимизация по всем N переменным образует полный цикл, называемый внешним. Количество внешних циклов, т. е. повторений внутренних циклов, заранее неизвестно и определяется сходимостью вычислительного процесса, которая зависит от свойств минимизируемой функции F(x) и выбора исходного приближения х°. На рис. 1 штриховой линией показана траектория спуска. Несмотря на простоту реализации и малый объем вычислений на шаге, часто от метода приходится отказываться из-за неудовлетворительной сходимости. На рис. 2 приведена геометрическая интерпретация так называемой «овражной» функции для двумерной задачи F(x1, х2). Если «дно оврага» не совпадает с направлением координатных осей, то количество шагов становится неприемлемо большим.
19.1 Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод в сочетании с методом наискорейшего спуска
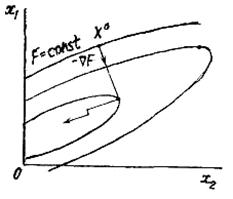 В градиентных методах движение всегда осуществляется в направлении наибольшего убывания целевой функции
В градиентных методах движение всегда осуществляется в направлении наибольшего убывания целевой функции 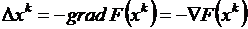 . Вектор градиента определяется через производные функции F(x) по всем независимым переменным
. Вектор градиента определяется через производные функции F(x) по всем независимым переменным 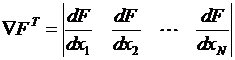 .
.
Таким образом, чтобы воспользоваться рекуррентным выражением градиентного метода  , необходимо на каждом шаге итерационного процесса вычислять значения производных
, необходимо на каждом шаге итерационного процесса вычислять значения производных 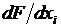 . Для организации скорейшего спуска необходимо определение оптимальной длины шага
. Для организации скорейшего спуска необходимо определение оптимальной длины шага 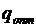 , которая в этом случае удовлетворяет условию
, которая в этом случае удовлетворяет условию 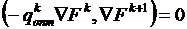 . Это условие означает, что результирующий вектор спуска
. Это условие означает, что результирующий вектор спуска 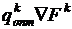 должен быть таким, чтобы новый градиент стал ортогонален предыдущему.
должен быть таким, чтобы новый градиент стал ортогонален предыдущему.
Рассмотрим два наиболее распространенных критерия окончания расчета, на основании которых можно судить о степени близости к экстремуму и к окончанию расчета.
Первый критерий основан на сопоставлении функции цели на двух соседних шагах k и к+1. Если убывание целевой функции мало, т. е. 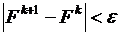 , где
, где 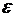 – заданная некоторая малая величина, то принимается, что найдено приближенное значение минимума F. Точность отыскания экстремума регулируется величиной
– заданная некоторая малая величина, то принимается, что найдено приближенное значение минимума F. Точность отыскания экстремума регулируется величиной 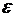 : чем меньше
: чем меньше 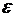 , тем точнее решение, но тем больше потребуется итерационных шагов, так как при приближении к экстремуму сходимость методов возможных направлений замедляется.
, тем точнее решение, но тем больше потребуется итерационных шагов, так как при приближении к экстремуму сходимость методов возможных направлений замедляется.
Преимущество первого критерия заключается в простоте реализации, однако в некоторых случаях он не соответствует приближению к экстремуму. Например, при отыскании минимума функции с оврагом, когда две соседние точки xk+1 и xk оказываются на дне оврага. Убывание целевой функции будет мало, хотя решение далеко не оптимально.
Более строгим является второй критерий — проверка длины градиента 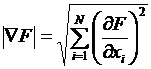 при отыскании абсолютного минимума F. Во втором критерии используется тот факт, что в точке экстремума все частные производные
при отыскании абсолютного минимума F. Во втором критерии используется тот факт, что в точке экстремума все частные производные 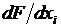 равны нулю, поэтому итерационный спуск осуществляется до получения
равны нулю, поэтому итерационный спуск осуществляется до получения 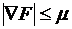 , где
, где  – малая заданная величина.
– малая заданная величина.
В некоторых случаях используют модификацию второго критерия и не проверяют длину вектора градиента, а сравнивают максимальную компоненту вектора градиента с некоторой заданной контрольной величиной.
Расчет по второму критерию связан с большим объемом вычислений, но он гарантирует правильность окончания расчета. В градиентных методах это наиболее рациональный способ прерывания циклического итерационного расчета, поскольку частные производные и так вычисляются для организации спуска.
Градиентный метод в сочетании с методом наискорейшего спуска.
1. Задаем начальные приближения 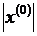 .
.
2. Находим значение целевой функции  и антиградиента
и антиградиента 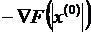 в точке
в точке 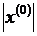 .
.
3. Делам пробные шаги и находим  .
.
4. Определяем оптимальную длину шага 
5. Определяем новые приближения оптимизируемых параметров  .
.
6. Проверяем выполнение критерия оптимальности 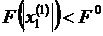 .
.
Вторая итерация выполняется аналогично. Далее проверяем критерий окончания расчетов:  При выполнении условия расчеты заканчиваются, при невыполнении продолжаем итерации.
При выполнении условия расчеты заканчиваются, при невыполнении продолжаем итерации.
20.1 Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента
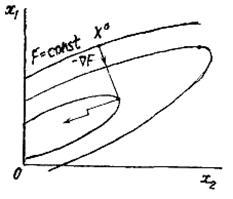 В градиентных методах движение всегда осуществляется в направлении наибольшего убывания целевой функции
В градиентных методах движение всегда осуществляется в направлении наибольшего убывания целевой функции 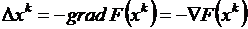 . Вектор градиента определяется через производные функции F(x) по всем независимым переменным
. Вектор градиента определяется через производные функции F(x) по всем независимым переменным 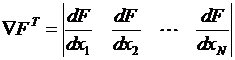 .
.
Таким образом, чтобы воспользоваться рекуррентным выражением градиентного метода  , необходимо на каждом шаге итерационного процесса вычислять значения производных
, необходимо на каждом шаге итерационного процесса вычислять значения производных 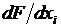 . Для организации скорейшего спуска необходимо определение оптимальной длины шага
. Для организации скорейшего спуска необходимо определение оптимальной длины шага 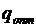 , которая в этом случае удовлетворяет условию
, которая в этом случае удовлетворяет условию 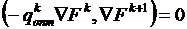 . Это условие означает, что результирующий вектор спуска
. Это условие означает, что результирующий вектор спуска 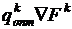 должен быть таким, чтобы новый градиент стал ортогонален предыдущему.
должен быть таким, чтобы новый градиент стал ортогонален предыдущему.
Достоинство этого метода состоит в том что, несмотря на сложность и большой объем вычислений на каждом шаге, он в сочетании с методом наискорейшего спуска дает очень быструю сходимость.
Метод проектирования градиента. Пусть требуется найти минимум выпуклой функции при условии, что независимые переменные удовлетворяют системе из P линейных ограничений в форме неравенств, т. е. 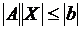
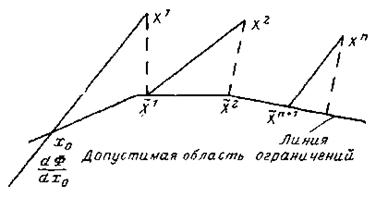
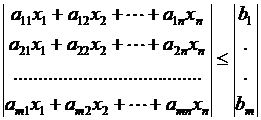 .
.
В начальной точке Х°, фазовые координаты которой удовлетворяют условиям ограничений 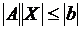 , определяется вектор-градиент и в направлении антиградиента производится движение за границу допустимой области до точки x':
, определяется вектор-градиент и в направлении антиградиента производится движение за границу допустимой области до точки x':  , где
, где 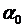 –множитель, определяющий величину шага за границу допустимой области.
–множитель, определяющий величину шага за границу допустимой области.
20.2 Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента
Полученная точка X1 проектируется на поверхность ограничений 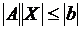 , в результате чего определится точка
, в результате чего определится точка 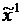 . Затем из точки
. Затем из точки 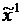 так же как и из точки Х°, в направлении антиградиента совершается движение за границу допустимой области в точку
так же как и из точки Х°, в направлении антиградиента совершается движение за границу допустимой области в точку 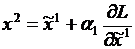 .
.
Полученная точка X2 проектируется на поверхность ограничений, в результате чего получается точка 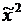 и т. д.
и т. д.
Если начальная точка Х° находится вне допустимой области, она вначале должна быть спроектирована на поверхность ограничений, после чего осуществляется описанная процедура движения. Это позволяет решать задачу от любого начального приближения.
21.1 Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент
При решении задачи оптимизации режима должны учитываться уравнения связи, дающие зависимости между переменными y и x. Количество зависимых переменных M определяется числом уравнений связи, которые можно рассматривать как ограничения, выраженные в форме равенств. В качестве таких ограничений обычно принимаются УУН, записанные в форме баланса токов каждого узла, кроме балансирующего или в форме баланса мощностей каждого узла 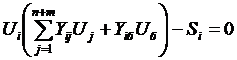 (1), где
(1), где 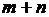 – общее число узлов в системе без балансирующего. Целевую функцию можно представить в виде
– общее число узлов в системе без балансирующего. Целевую функцию можно представить в виде 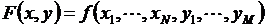 , где x, y – векторы независимых и зависимых переменных, связь между которыми выражается системой уравнений в виде вектор – функции
, где x, y – векторы независимых и зависимых переменных, связь между которыми выражается системой уравнений в виде вектор – функции 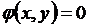 .
.
В градиентном методе необходимо определить направление  максимального уменьшения целевой функции, не нарушая связей между переменными. Поэтому найдем связь между приращениями зависимых
максимального уменьшения целевой функции, не нарушая связей между переменными. Поэтому найдем связь между приращениями зависимых  и независимых
и независимых  переменных.
переменных.
Рассмотрим точку (х°, у°) с координатами  , удовлетворяющую системе равенств
, удовлетворяющую системе равенств 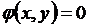 :
: 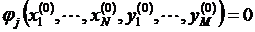 (2),
(2), 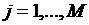 .
.
Это означает, что рассматриваются режимы энергосистемы, удовлетворяющие (1).
Разложив нелинейные уравнения 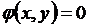 в точке (х°, y°) в ряд Тейлора и ограничившись членами, содержащими производные не выше первого порядка, получим
в точке (х°, y°) в ряд Тейлора и ограничившись членами, содержащими производные не выше первого порядка, получим 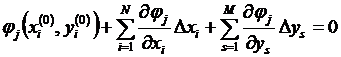 ,
, 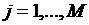 .
.
С учетом (2) в матричной записи последняя система уравнений приобретает вид 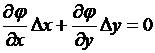 , откуда, переходя к бесконечно малым приращениям, получим
, откуда, переходя к бесконечно малым приращениям, получим  (3).
(3).
Здесь 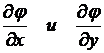 – матрицы частных производных уравнений связи по независимым и зависимым переменным.
– матрицы частных производных уравнений связи по независимым и зависимым переменным.
С учетом зависимости y(x) целевую функцию F(x,y) можно представить как F(x, y(x)). Выражение градиента приобретает вид
21.2 Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент

что в матричной форме записывается двумя способами:
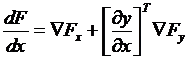 ;
;  (4),
(4),  ,
, 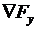 – векторы - столбцы частных производных целевой функции по независимым и зависимым переменным.
– векторы - столбцы частных производных целевой функции по независимым и зависимым переменным.
Вектор производных целевой функции по независимым переменным dF/dx называется приведенным градиентом. С учетом соотношения (3) представим (4) в виде 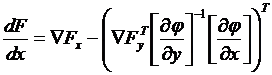 .
.
Вектор dF/dx рассматривается как возможное направление и используется в рекуррентном выражении итерационной процедуры  .
.
Наряду с методом приведенного градиента ограничения в форме равенств учитывает также метод Лагранжа. При отыскании экстремума целевой функции с учетом ограничений в форме равенств методом Лагранжа вводится новая функция Лагранжа L, в которой все переменные рассматриваются как независимые. В данном случае нет необходимости вычислять матрицу частных производных [dу/dx], в чем и заключается преимущество метода по сравнению с предыдущим. Недостатком метода является увеличение размерности задачи за счет введения неопределенных множителей Лагранжа, число которых равно числу уравнений связи.
22.1 Учет ограничений в форме неравенств при решении задач опт-ии в электроэнергетике. Метод штрафных функций
При оптимизации режима электрической системы задается совокупность ограничений в форме неравенств 

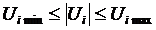 , определяющая некоторую допустимую область D. В задаче нелинейного программирования необходимо отыскивать относительный экстремум в области D, допуская, что активным может оказаться любое ограничение. В некоторых случаях активные ограничения могут быть выявлены в ходе итерационного процесса решения задачи оптимизации.
, определяющая некоторую допустимую область D. В задаче нелинейного программирования необходимо отыскивать относительный экстремум в области D, допуская, что активным может оказаться любое ограничение. В некоторых случаях активные ограничения могут быть выявлены в ходе итерационного процесса решения задачи оптимизации.
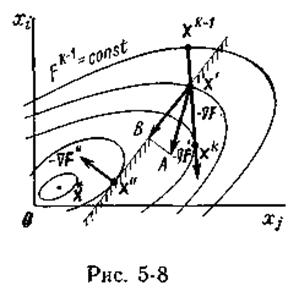 Пусть
Пусть 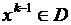 . В результате шага по рекуррентному выражению метода возможных направлений получается точка xk. Если эта точка также принадлежит области D, то осуществляется переход к точке xk+1. Если же
. В результате шага по рекуррентному выражению метода возможных направлений получается точка xk. Если эта точка также принадлежит области D, то осуществляется переход к точке xk+1. Если же 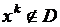 , то необходимо найти граничную точку xk на поверхности области D. В результате выявляется активное ограничение (рис. 5-8), которое можно рассматривать как равенство. Однако правомерность такого перехода должна быть обоснована, так как не исключаются ситуации, подобные представленной на рис. 5-8. Здесь точка
, то необходимо найти граничную точку xk на поверхности области D. В результате выявляется активное ограничение (рис. 5-8), которое можно рассматривать как равенство. Однако правомерность такого перехода должна быть обоснована, так как не исключаются ситуации, подобные представленной на рис. 5-8. Здесь точка 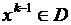 . Движение по антиградиенту
. Движение по антиградиенту 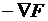 с оптимальной длиной шага приводит в точку
с оптимальной длиной шага приводит в точку 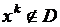 . Пусть найдена граничная точка x'. Если в дальнейшем ограничение рассматривать как равенство, то будет найден экстремум на ограничивающей поверхности в точке x". Как видим, в данном случае решение оказывается неправильным, так как фактически следует найти точку абсолютного минимума
. Пусть найдена граничная точка x'. Если в дальнейшем ограничение рассматривать как равенство, то будет найден экстремум на ограничивающей поверхности в точке x". Как видим, в данном случае решение оказывается неправильным, так как фактически следует найти точку абсолютного минимума  .
.
Метод штрафных функций. Для решения задачи отыскания экстремума целевой функции F (x,y) в допустимых областях Dy и Dz рассматривается новая функция  , которая в отличие от F(x,у) определена в пространстве зависимых переменных при
, которая в отличие от F(x,у) определена в пространстве зависимых переменных при  и
и 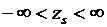 (где
(где 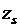 рассматриваются в виде переменных, зависимых от x и у). Это свойство новой функции и достигается за счет введения штрафных функций Ш(y) и Ш(z), подчиняющихся условиям:
рассматриваются в виде переменных, зависимых от x и у). Это свойство новой функции и достигается за счет введения штрафных функций Ш(y) и Ш(z), подчиняющихся условиям:

 .
.
22.2 Учет ограничений в форме неравенств при решении задач опт-ии в электроэнергетике. Метод штрафных функций
Эти условия означают следующее: если взята некоторая точка хk так, что соответствующие ей зависимые переменные yk и zk удовлетворяют ограничениям  и
и 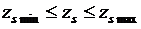 , то штраф равен нулю, в противном случае накладывается штраф в виде некоторой положительной добавки к исходной функции F(x,у). Чем существенней отклонение от допустимой области, тем больше величина штрафа. А так как методы возможных направлений в этом случае основываются на построении такой траектории х°, х1,..., хk, в которой Wk<Wk-1, то при надлежащем выборе функции штрафа движение всегда будет происходить в сторону допустимой области.
, то штраф равен нулю, в противном случае накладывается штраф в виде некоторой положительной добавки к исходной функции F(x,у). Чем существенней отклонение от допустимой области, тем больше величина штрафа. А так как методы возможных направлений в этом случае основываются на построении такой траектории х°, х1,..., хk, в которой Wk<Wk-1, то при надлежащем выборе функции штрафа движение всегда будет происходить в сторону допустимой области.
Штрафные функции должны удовлетворять двум условиям: 1) при их использовании не должны появляться новые локальные минимумы и абсолютный минимум функции W должен совпадать с относительным минимумом исходной целевой функции или быть достаточно близким ему; 2) функция штрафа должна возрастать при увеличении степени нарушения ограничения.
Способ задания квадратичной штрафной функции вида 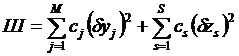 , где
, где 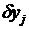 ,
, 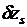 – величины, характеризующие степень нарушения соответствующих ограничений. Коэффициенты штрафа
– величины, характеризующие степень нарушения соответствующих ограничений. Коэффициенты штрафа 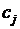 и
и 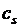 имеют смысл коэффициентов приведения штрафа к размерности целевой функции.
имеют смысл коэффициентов приведения штрафа к размерности целевой функции.
Выбор коэффициента штрафа существенно влияет на сходимость итерационного процесса и точность отыскания минимума целевой функции. Чем больше величина 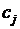 , тем круче растет функция W вне области D и тем заметнее функция W приобретает свойства «овражности». Чаще всего при овражных функциях удовлетворительная сходимость не обеспечивается. Коэффициент штрафа влияет и на траекторию спуска.
, тем круче растет функция W вне области D и тем заметнее функция W приобретает свойства «овражности». Чаще всего при овражных функциях удовлетворительная сходимость не обеспечивается. Коэффициент штрафа влияет и на траекторию спуска.
23.1 Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе
Преимущество метода Ньютона заключается в том, что количество итерационных шагов невелико. Как и во всяком итерационном методе, расчет начинается с задания некоторой исходной точки 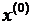 , для которой можно вычислить значение функции
, для которой можно вычислить значение функции  . Аппроксимируем в точке
. Аппроксимируем в точке 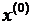 зависимость f(x) некоторой другой функцией
зависимость f(x) некоторой другой функцией 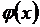 путем разложения в ряд f(x) и сохранения членов, содержащих вторые производные:
путем разложения в ряд f(x) и сохранения членов, содержащих вторые производные:  (1).
(1).
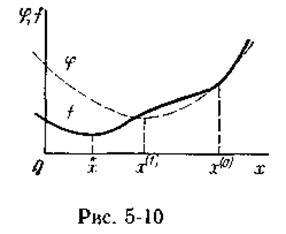 Такая аппроксимация соответствует замене исходной функции f(x) параболой
Такая аппроксимация соответствует замене исходной функции f(x) параболой 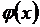 , совпадающей в точке
, совпадающей в точке 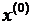 по значениям первой и второй производных (рис. 5-10). Если обозначить через
по значениям первой и второй производных (рис. 5-10). Если обозначить через  величину отклонения от
величину отклонения от 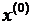 , то вместо (1) можно записать
, то вместо (1) можно записать  (2).
(2).
Найдем такое значение приращения  , которое обращает в минимум
, которое обращает в минимум 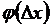 . Для этого приравняем нулю производную от (2):
. Для этого приравняем нулю производную от (2): 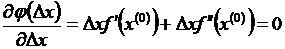 , откуда
, откуда 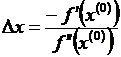 . Следовательно, точку
. Следовательно, точку 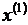 экстремума
экстремума 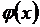 можно найти из условия
можно найти из условия  .
.
Если в этой точке производная  существенно отличается от нуля, то эту точку следует рассматривать как исходную и повторить вычисления. В общем виде рекуррентное выражение итерационного процесса можно представить как
существенно отличается от нуля, то эту точку следует рассматривать как исходную и повторить вычисления. В общем виде рекуррентное выражение итерационного процесса можно представить как 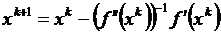 .
.
Таким образом, суть метода заключается в том, что исходная функция заменяется полиномом второй степени – параболой – и затем отыскивается ее минимум. В новой точке аппроксимация повторяется, отыскивается ее минимум и т. д.
Аналогично функцию двух переменных F(х1, х2), которая аппроксимируется разложением в ряд Тейлора, можно представить как 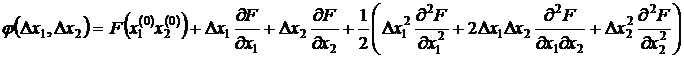 (3).
(3).
Градиент этой новой функции в точке ее экстремума равен нулю:
23.2 Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе
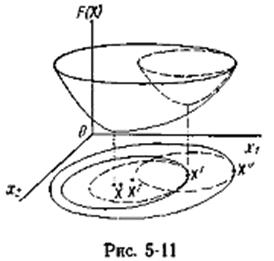
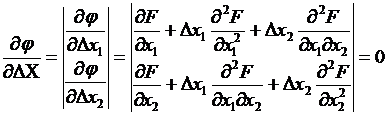 (4). Решая эту систему относительно
(4). Решая эту систему относительно 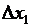 и
и 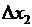
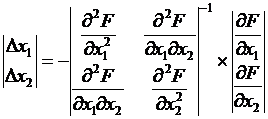 (5), находим точку экстремума, а следовательно, и точку нового приближения х1:
(5), находим точку экстремума, а следовательно, и точку нового приближения х1: 
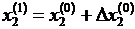 (6).
(6).
Геом-я интерпретация рассмотренного случая представлена на рис. 5-11. Истинная зависимость F(x) заменена параболоидом 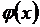 , линии равного уровня которого в проекции на плоскость осей x1 и х2 - эллипсы. Решение системы (4) позволяет найти центр эллипсов х1, а затем в этой точке повторить аппроксимацию и найти точку х2 и т. д.
, линии равного уровня которого в проекции на плоскость осей x1 и х2 - эллипсы. Решение системы (4) позволяет найти центр эллипсов х1, а затем в этой точке повторить аппроксимацию и найти точку х2 и т. д.
Выражения (3–6) соответствуют общему случаю минимизации функции многих переменных F(x). В векторно – матричной форме эти выражения приобретают вид 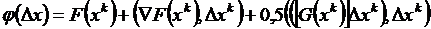 ;
; 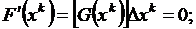

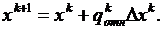
Функция 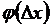 позволяет найти приближенное значение исходной функции F(x) и совпадает с ней лишь в точке разложения х°. В первом из этих выражений второй и третий члены – скалярные произведения векторов, отделенных друг от друга запятой. Через [G(x)] обозначена матрица вторых частных производных:
позволяет найти приближенное значение исходной функции F(x) и совпадает с ней лишь в точке разложения х°. В первом из этих выражений второй и третий члены – скалярные произведения векторов, отделенных друг от друга запятой. Через [G(x)] обозначена матрица вторых частных производных: 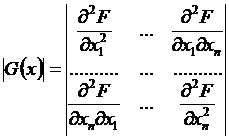 , называемая матрицей Гессе. Эта матрица всегда симметрична. Вектор F'(x) есть вектор первых частных производных целевой функции и, следовательно, это есть градиент
, называемая матрицей Гессе. Эта матрица всегда симметрична. Вектор F'(x) есть вектор первых частных производных целевой функции и, следовательно, это есть градиент  .
.
24.1 Комплексная оптимизация режимов энергосистемы
В общем случае для получения решения приходится применять современные методы нелинейного программирования. Рассмотрим применение для этой задачи метода приведенного градиента.
Любая задача нелинейного математического программирования может быть записана в следующей форме. Имеется функция многих переменных 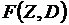 .
.
Компоненты Z являются искомыми параметрами режима, a D включает известную исходную информацию о состоянии системы, тогда min F(Z, D) совпадает с min F(Z). Необходимо по Z минимизировать функцию 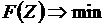 при ограничениях
при ограничениях 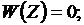
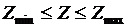 .
.
При использовании метода приведенного градиента компоненты вектора параметров режима системы Z разделяются на два подмножества X и Y: Y включает независимые переменные, т. е. те параметры, которые в системе могут регулироваться, на которые можно воздействовать, используя определенные средства управления; X включает зависимые параметры режима, т. е. те, которые могут быть вычислены по параметру Y, тогда 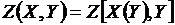 , отсюда
, отсюда 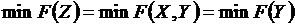 , а ограничения принимают вид:
, а ограничения принимают вид:
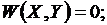
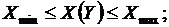
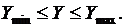
Связи между независимыми Y и зависимыми X переменными, как правило, неявные. Поэтому задача минимизации функции (6-G7) решается по многошаговой схеме.
Деление параметров режима Z на два подмножества X и Y понижает размерность задачи и, следовательно, облегчает вычислительный процесс. Действительно, если Z имеет n переменных, а X имеет m переменных, то обычно размерность задачи p<<n.
Рассмотрим основные положения решения задачи комплексной оптимизации методом приведенного градиента. ЭС состоит из i = 1, 2, ..., М обобщенных и отдельных узлов и имеются только тепловые станции. Параметры режима: 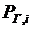 ,
, 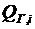 – активные и реактивные мощности генераторных узлов;
– активные и реактивные мощности генераторных узлов; 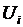 ,
,  – модули напряжений и фазовые углы в узлах системы. Известны активные и реактивные нагрузки в узлах, причем они не зависят от напряжений и частоты системы. Требуется определить оптимальное распределение нагрузки по условию минимума расхода условного топлива системы.
– модули напряжений и фазовые углы в узлах системы. Известны активные и реактивные нагрузки в узлах, причем они не зависят от напряжений и частоты системы. Требуется определить оптимальное распределение нагрузки по условию минимума расхода условного топлива системы.
24.2 Комплексная оптимизация режимов энергосистемы
1. Уравнение цели 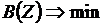 .
.
Вектор параметров Z разделяется на вектор независимых переменных  и зависимых переменных
и зависимых переменных 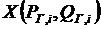
Тогда можно записать 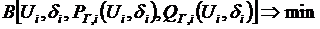 .
.
2. Уравнения связи включают:
– эквивалентные характеристики генераторных узлов вида 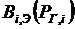 , где
, где 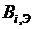 – эквивалентный расход условного топлива;
– эквивалентный расход условного топлива;
– связи между параметрами X и Y, которые имеют вид Y(Х);
3. Уравнения ограничений, которые задаются в виде неравенств
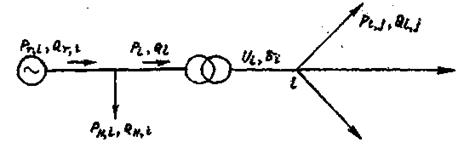

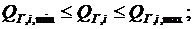
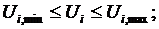
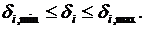
Задаются также балансовые ограничения по активным и реактивным мощностям в виде системы уравнений установившегося режима (рис.).
Для каждого узла небаланс по мощности равен: 
 , где
, где  и
и  – функция небаланса по активной и реактивной мощностям.
– функция небаланса по активной и реактивной мощностям.
Когда в стационарном режиме в узлах системы имеется баланс, то 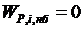 ,
, 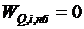 . Если в стационарном режиме изменить независимые переменные
. Если в стационарном режиме изменить независимые переменные 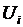 ,
,  , то появится небаланс и
, то появится небаланс и 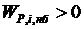 ,
,  . Меняя
. Меняя 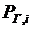 ,
, 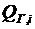 , можно получить новый допустимый стационарный режим для новых значений
, можно получить новый допустимый стационарный режим для новых значений 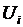 ,
,  . Задача и будет заключаться в том, чтобы найти такое решение уравнений установившегося режима, при котором
. Задача и будет заключаться в том, чтобы найти такое решение уравнений установившегося режима, при котором 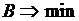 .
.
4. Вычисление приведенного градиента. Решение считается оптимальным, если модуль градиент - вектора 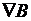 функции В (Х, Y) будет меньше заданного малого значения, т. е.
функции В (Х, Y) будет меньше заданного малого значения, т. е. 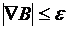 .
.
1. Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы
2. Применение метода множителей Лагранжа при решении задач оптимизации в ЭЭ
3. Опт-е распределение перетоков мощности в замкнутых контурах эл. сети
4. Прим-ие м-да множителей Л. для опт-ии перетоков мощности в эл. сети
5. Оптимизация распределения перетоков мощности сложной эл. сети
6. Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС
7. Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Структурная схема алгоритма
8. Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь P. Физический смысл равенства относительных приростов
9. Определение опт. распределения нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относит. приросты ТЭС и ГЭС
10. Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме
11. Оптимальное распределение нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения
12. Оптимальное распределение нагрузки при переменном напоре ГЭС
13. Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения агрегатов электростанций
14. Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования. Основные определения
15. Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике
16. Применение метода наискорейшего спуска при решении задач опт-ии в ЭЭ
17. Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике
18. Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода
19. Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод + метод наискорейшего спуска
20. Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента
21. Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент
22. Учет ограничений в форме неравенств при решении задач оптимизации в электроэнергетике. Метод штрафных функций
23. Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе. Геометрическая интерпретация аппроксимации ЦФ
24. Комплексная оптимизация режимов энергосистемы
Дата добавления: 2018-02-15; просмотров: 2158; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
