Композиции двумерных преобразований
Nbsp;
Математические основы компьютерной графики
Преобразование объектов и систем координат на плоскости
В современной компьютерной графике широко используется координатный метод. Независимо от выбранного метода проектирования необходимо иметь в памяти компьютера численные данные, описывающие исследуемый объект в некоторой системе координат. Каждая точка на экране (или на бумаге) задается координатами. Координаты используются для описания объектов на плоскости и в пространстве. При выполнении многих промежуточных действий отображения объекта или объектов используют разные системы координат и различные преобразования из одной системы в другую.
Рассмотрим некоторые преобразования объектов и покажем связь этих преобразований с соответствующими преобразованиями координат.
Перенос
Перенос объекта
Если объект переносится без поворота, связь между радиус-вектором 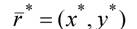 перемещенной точки и ее первоначальным положением
перемещенной точки и ее первоначальным положением 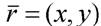 устанавливается соотношением (рис.2.1):
устанавливается соотношением (рис.2.1):
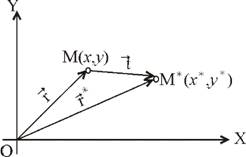
Рис.2.1. Перенос объекта
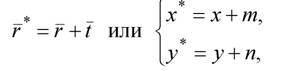
где t =(т,п) - вектор перемещения каждой точки рассматриваемого объекта.
Перенос системы координат
С другой стороны, если таким же способом переносятся оси координат, когда объект (точка) фиксирован (рис 2.2), то связь между векторами задается следующим соотношением:
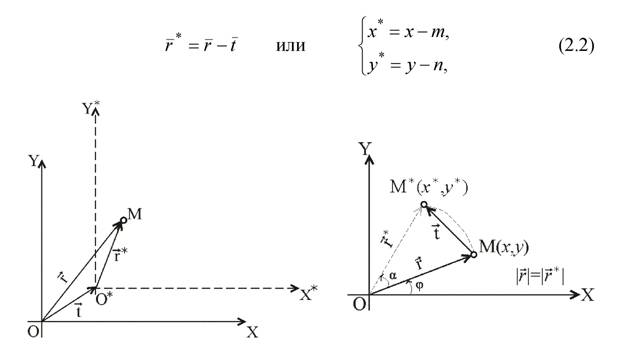
Рис.2.2. Перенос осей координат Рис.2.3. Поворот объекта
|
|
|
Поворот относительно начала координат
Поворот объекта
Если все точки некоторого объекта M(x,y) повернуть относительно начала координат на некоторый угол α, то, как следует из графика на рис.2.3, полярные координаты точки 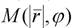 в результате поворота изменятся на координаты точки
в результате поворота изменятся на координаты точки 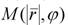 . Используя формулу связи полярных и декартовых координат, будем иметь:
. Используя формулу связи полярных и декартовых координат, будем иметь:
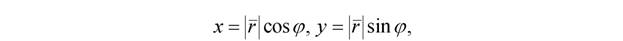
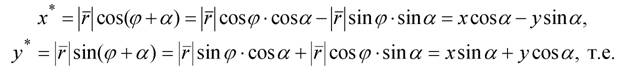
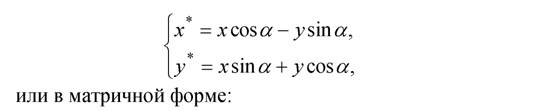 (2.3)
(2.3)
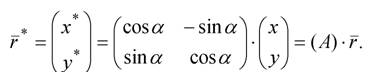 (2.4)
(2.4)
Поворот осей координат
Если оси координат повернуть описанным выше способом, то рассматриваемый объект (точка М) в новой системе координат как бы повернется на угол α(рис.2.4). В этом случае:
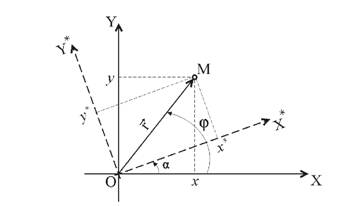
Рис.2.4. Поворот системы координат
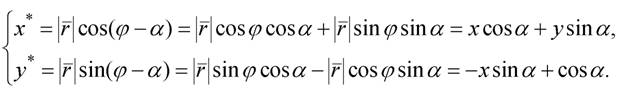 (2.4)
(2.4)
или в матричной форме записи
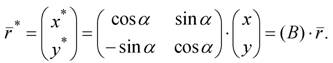 (2.5)
(2.5)
Совершенно очевидно, что (А)=(ВТ), т.е. между преобразованием объекта и преобразованием координат установлена очень простая связь.
Масштабирование точки
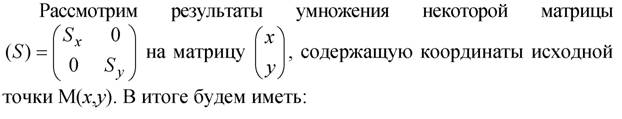
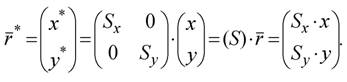 (2.7)
(2.7)
Из формулы (2.7) следует, что в результате такого произведения происходит масштабирование координат точки М (рис.2.5).
Рис.2.5. Масштабирование точки
Преобразование сдвига точки
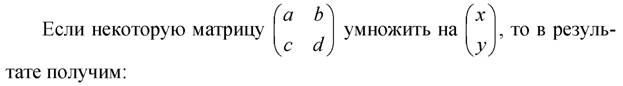
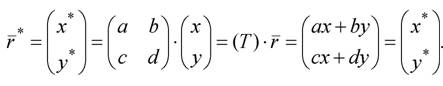 (2.8)
(2.8)
Полученный результат означает, что исходные координаты x и y точки М преобразуются в новые координаты x* и y* новой точки M*, т.е. происходит преобразование сдвига точки.
|
|
|
Примеры преобразования объектов на плоскости
Поворот
Рассмотрим треугольник АВС (рис.2.7) и с помощью соответствующего преобразования повернем его на 90° против часовой стрелки относительно начала координат. С этой целью воспользуемся формулой (2.4):
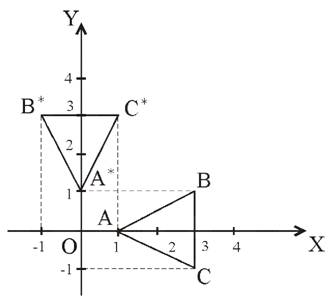
Рис.2.7. Поворот объекта на 900 против
часовой стрелки относительно начала
координат
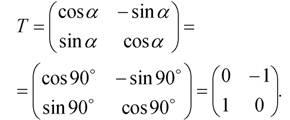
Если использовать матрицу размером (2x3), состоящую из координат x и y соответствующих вершин треугольника, то можно записать:
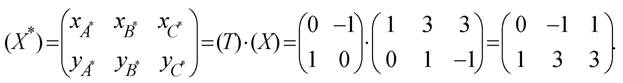
Таким образом получены координаты нового треугольника А * В * С *, повернутого на угол 90° против часовой стрелки. С учетом формулы (2.4) можно получить матрицы преобразований и для других углов поворота относительно начала координат, например на угол 180° и 270° против часовой стрелки:
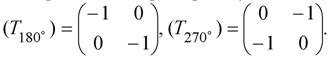
Отражение
В то время как поворот на плоскости OXY осуществляется в двумерном пространстве относительно нормали к этой координатной плоскости, отражение представляет собой поворот на 180° плоского объекта в трехмерном пространстве относительно соответствующей оси, лежащей в плоскости OXY. На рис.2.8 представлены примеры двух отражений треугольника АВС.
|
|
|
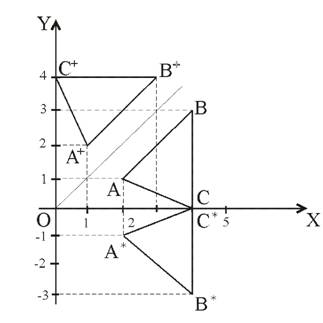
Рис.2.8. Отражение объекта на
плоскости
Отражение относительно прямой OX (y=0) получено с использованием матрицы 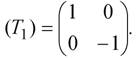
Вершины нового треугольника А*В*С* определяются следующим преобразованием:
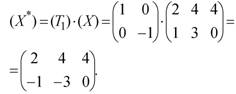
Отражение треугольника АВС относительно прямой осуществляется с помощью матрицы 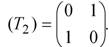 Выполнив необходимые преобразования, получим координаты вершин треугольника А+В+С+:
Выполнив необходимые преобразования, получим координаты вершин треугольника А+В+С+:
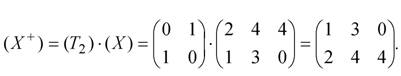

Масштабирование объекта
В соответствие с формулой (2.7) (масштабирование точки) и данными раздела 2.5, можно сделать вывод о том, что и в случае с масштабированием плоского объекта можно использовать матрицу преобразования с ненулевыми диагональными элементами матрицы
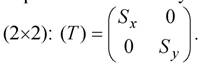
Если значения диагональных элементов S x и Sy матрицы (Т) равны, то имеет место равномерное масштабирование исходного треугольника АВС в треугольник А*В*С* относительно точки начала координат (рис.2.9).
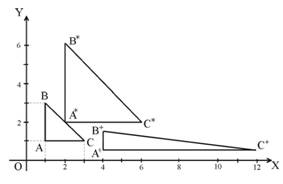
Рис.2.9. Масштабирование объекта на плоскости
Например, при Sx=Sy=2будем иметь:
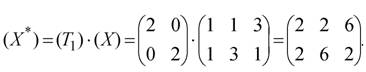
Если значения диагональных элементов матрицы (Т) не равны друг другу, например Sx=4, S y=1/2, то в этом случае исходный ∆АВС искажается и преобразуется в ∆А+ В+С+ (рис.2.9):
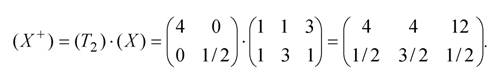
Выполненные операции приводят не только к изменению геометрии объекта, но и к его перемещению. Это объясняется тем, что в рассмотренных случаях масштабируются координатные векторы, а не ребра треугольника. Для того чтобы получить “чистое” масштабирование объекта без эффекта перемещения, необходимо центр фигуры поместить в начало координат.
|
|
|
Однородные координаты
В научной и учебной литературе очень часто точка с координатами (x,y) ассоциируется с вектором, проведенным в эту точку из начала координат. Эта ассоциация может привести к недоразумениям. Например, вектор из точки А(1,1) в точку В(2,3) (рис.2.10) равен вектору OP, проведенному из точки (0,0) в точку (1,2), поскольку оба эти вектора имеют одинаковый модуль и направление.
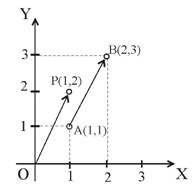
Рис.2.10. Иллюстрация различий в представлении точек и векторов
Пренебрежение различием в представлении точек и векторов серьезно усложняет реализацию системы компьютерной графики. Поэтому предпочтительнее выбрать такой способ представления, который позволит легко отличать точки от векторов.
Действительно, выше было показано, что преобразования вращения, сдвига и масштабирования могут быть выражены с помощью уравнений вида:
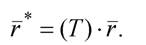 (2.9)
(2.9)
Однако каждое из этих уравнений справедливо лишь для преобразований относительно начала координат. Если же преобразования происходят не относительно начала координат, эти преобразования необходимо сочетать с переносами, которые можно описать формулой типа
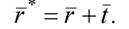 (2.10)
(2.10)
Если выразить точки в однородных координатах, то все преобразования можно будет реализовать с помощью формул умножения типа (2.9). В однородных координатах точка М(x , y) записывается как M(wx, wy, w) для некоторого масштабного множителя w≠0. При этом если для точки задано ее представление в однородных координатах M(X;Y;W), то легко можно найти ее декартовы координаты:
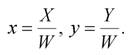 (2.11)
(2.11)
Как правило, выбирают W=1, поэтому операция деления не требуется. Однородные координаты можно представить как вложение промасштабированной с коэффициентом W двумерной плоскости в плоскость z=W (z=1) в трехмерном пространстве. Таким образом, в однородной системе координат вектор, определяющий местоположение точки на плоскости, записывается следующим образом:
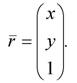 (2.12)
(2.12)
Если нас интересуют матричные свойства кривых, то необходимо установить связь между однородными и декартовыми координатами в соответствии с соотношениями (2.11). Однако для определения многих неметрических свойств геометрических фигур установление такой связи не требуется. Эти описательные свойства составляют предмет исследования проективной геометрии, основные положения которой будут рассмотрены ниже.
Кроме преимуществ, обусловленных унификацией описания преобразований координат, применение однородных координат дает возможность избежать многих аномальных случаев, возникающих при работе с декартовыми координатами, таких, например, как непересечение параллельных прямых, а также устраняет необходимость устанавливать различие между центральными и нецентральными коническими сечениями.
В однородных координатах матрица, определяющая различные двумерные преобразования, может быть записана в следующем общем виде:
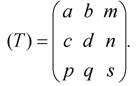 (2.13)
(2.13)
При этом матрица (2.13) может быть разделена на четыре составляющих части:
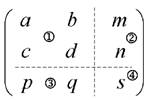 (2.14)
(2.14)
Первая часть (матрица 2x2) определяет преобразования сдвига, вращения и локального масштабирования. Вторая часть (тип) – определяет преобразования переноса. Третья часть (p и q) – отвечает за проецирование в однородных координатах. Четвертая часть (s) – производит пропорциональное (глобальное) масштабирование объекта.
Рассмотрим несколько примеров преобразований, основанных на использовании матрицы (2.13).
Перенос точки:
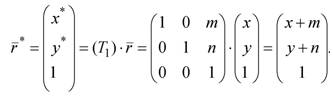
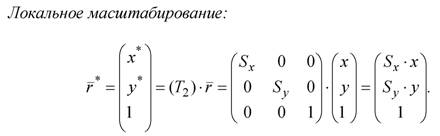
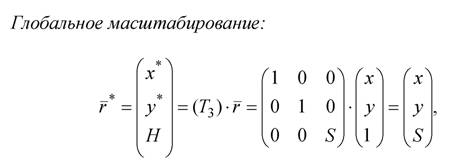
где x*=x, y*=y, H=S. После нормализации, т.е. деления координат на масштаб S, будем иметь 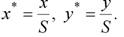
Таким образом подобное преобразование приводит к пропорциональному масштабированию соответствующего вектора. При S=1 масштаб не изменяется, при S>1 – происходит уменьшение, а при S<1 – увеличение масштаба (рис.2.11). Если S<1, то H=const задает плоскость, лежащую между плоскостями H=1 и H=0, например H=1/2. Следовательно, когда прямая А1В1 проецируется на плоскость Н=1, то А*В* увеличивается относительно А1В1. Если S>1, то Н=const определяет плоскость, расположенную слева от плоскости Н=1, например плоскость Н=2. В этом случае при проецирование прямой А2В2 на плоскость Н=1 происходит уменьшение отрезка прямой А*В*.
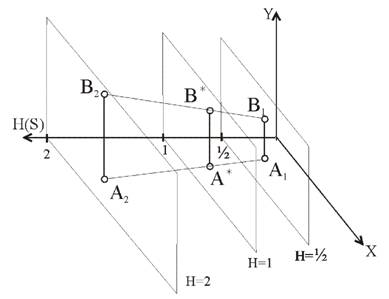
Рис. 2.11. Пропорциональное (глобальное масштабирование)
Проецирование – геометрическая интерпретация однородных координат:
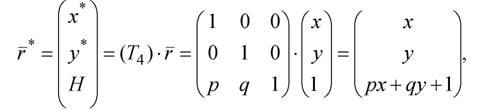
где x*=x, y*=y, H=px+qy+1. Н – определяет плоскость, содержащую преобразованные точки, представленные в однородных координатах. Пусть прямая АВ лежит в плоскости Н=1 (рис.2.12). А'B' – проекция этой прямой на плоскость px+qy+1=Н. После выполнения нормализации будем иметь:
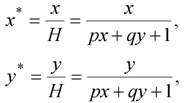 (2.15)
(2.15)
что соответствует координатам точек А* и В*, расположенных в плоскости Н=1. Если p=q=1, А(1,3), В(4,1), то с учетом формул (2.15) будем иметь:
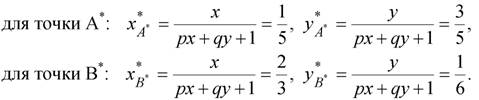
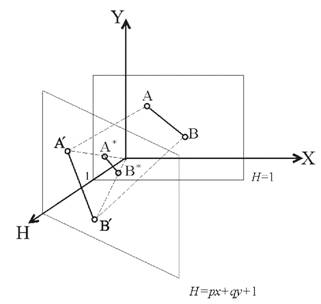
Рис.2.12. Преобразования проецирования в однородных координатах
Композиции двумерных преобразований
Матричное произведение называется объединением, или композицией матриц. Рассмотрим, каким образом можно использовать композиции преобразований для объединения отдельных матриц с целью получения желаемых общих результатов. Основное преимущество объединенных преобразований состоит в том, что в случае большого числа точек более эффективно применять одно результирующее преобразование, чем ряд последовательных преобразований друг за другом.
Предположим, что выполняются три последовательных преобразования точки r - (матрицы преобразований – (А), (В), (С)) и при этом формируется новая точка r*. Произведение матриц ассоциативно, но, поэтому можно записать последовательность указанных преобразований в следующем виде:
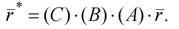 (2.16)
(2.16)
Порядок выполнения операций существенно влияет на производительность процесса вычислений. Например, можно сначала умножить матрицу (А) на координаты точки, затем матрицу (В) умножить на полученный результат, а уже затем матрицу (С) умножить на полученный результат:
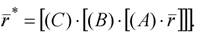 (2.17)
(2.17)
Для множества преобразованных точек операцию произведения целесообразно разбить на два этапа. Сначала определяется произведение квадратных матриц отдельных преобразований:
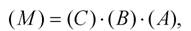 (2.18 )
(2.18 )
а затем полученная матрица (2.18) используется для обработки всего множества точек:
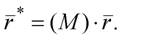 (2.19)
(2.19)
Покажем на конкретных примерах, как следует вычислять матрицу (М), т.е. строить композиции двумерных преобразований.
Пример.2.8.1. Поворот объекта относительно произвольной точки Р1 (рис.2.13, а)
Для выполнения этой задачи необходимо совершить последовательно три элементарных преобразования:
1) Перенос точки Р1 (объекта) в начало координат (точка P 1') (рис.2.13,б);
2) Поворот объекта относительно точки P1' (рис.2.13,в);
3) Перенос точки P 1'(объекта) на место точки Р1 (рис.2.13,г).
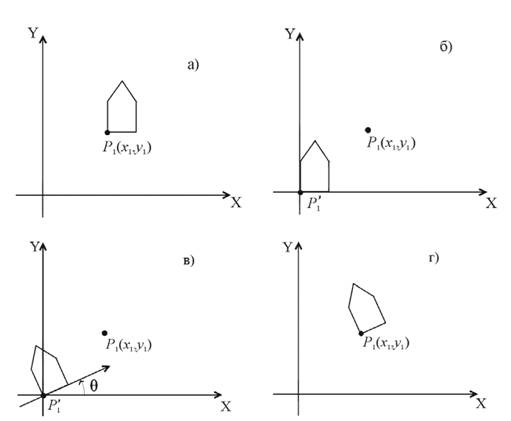
Рис. 2.13. Пример.2.8.1. Поворот объекта относительно точки Р1
Последовательность указанных преобразований имеет вид:

Предварительно перемножив матрицы (Т3), (Т2) и (Т1), получим результирующую матрицу (М):
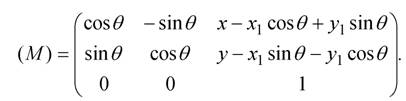
Пример.2.8.2. Изменить масштаб, повернуть и расположить объект в заданной точке Р2. Центр поворота и масштабирования точка Р1 (рис.2.14).
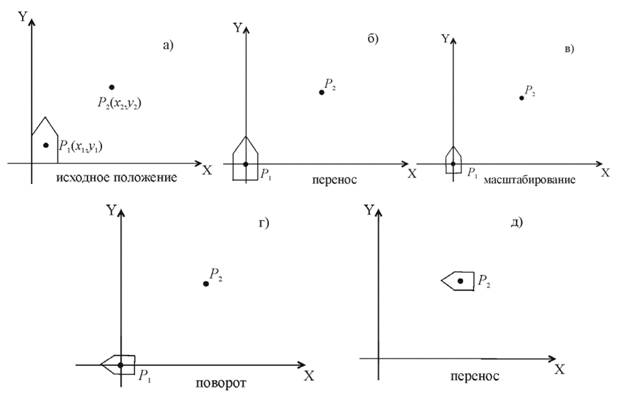
Рис.2.14. Пример.2.8.2. Изменить масштаб, повернуть и расположить объект в заданной точке
По аналогии с предыдущей задачей будем иметь:
(T4) (T3) (T2) (T1)
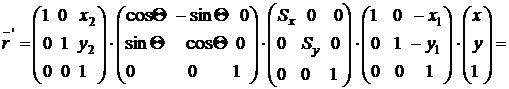
Перенос Поворот Изменение Перенос Р1
масштаба в начало
координат
= (T4)· (T3)· (T2)· (T1) = 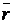 .
.
Перемножив матрицы (Т4), (Т3), (Т2) и (Т1), получим результирующую матрицу (М):

В общем случае умножение матриц не подчиняется свойству коммутативности, т.е. от перестановки матриц в произведение результат может измениться. В некоторых частных случаях можно не обращать внимание на порядок перемножения матриц: перенос *перенос, масштабирование *масштабирование, поворот *поворот, масштабирование при Sx=Sy *поворот. В противном случае необходимо соблюдать определенную последовательность перемножения матриц: первое преобразование находится в правой части равенства.
Дата добавления: 2018-02-18; просмотров: 1745; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
