ЭВОЛЮЦИЯ ВЗГЛЯДОВ НА ПРИРОДУ ТРЕНИЯ ТВЕРДЫХ ТЕЛ

⇐ ПредыдущаяСтр 2 из 10Следующая ⇒

В основе механизма трения твердых тел, несмотря на кажущуюся его простоту, лежат трудно поддающиеся исследованию весьма сложные молекулярно-механические процессы. Для того чтобы охарактеризовать современное состояние учения о внешнем трении, следует коротко рассмотреть эволюцию взглядов на его природу и остановиться на существующих теориях трения, получивших наибольшее признание.

Первые положения о закономерностях внешнего трения были изложены еще в работе Леонардо да Винчи, опубликованной в 1508 году.

В 1751 году Г.Амонтон подтвердил предположения Леонардо да Винчи и впервые сформулировал закон трения в следующем виде:

где F - сила трения; m - коэффициент пропорциональности (трения);

N - нагрузка (нормальная сила).

Амонтон считал, что сопротивление относительному смещению трущихся поверхностей связано исключительно с находящимися на поверхностях трения выступами, механически цепляющимися один за другой. По его мнению, коэффициент трения не зависит от нагрузки, формы и размеров трущихся поверхностей, а его величина определяется в основном природой и состоянием поверхности трущихся тел. Вследствие ограниченности знаний того времени относительно природы и строения поверхности трущихся тел ряд известных исследователей того времени Паран, Лейбниц, Орлов, Вышеградский, де Камюс, Эйлер, Делагер и другие в дальнейшем развивали взгляды на трение как на чисто механический процесс.

В начале XVIII века среди работ, направленных на выявление природы трения, стали появляться такие, в которых обнаруживались отклонения от закона Амонтона. Например, было установлено, что на более гладких поверхностях коэффициент трения выше, чем на более шероховатых. Это в корне противоречило механической теории трения того времени. В 1785 году Кулон предложил учитывать наблюдаемые на практике отклонения от закона Амонтона путем введения в него второго дополнительного члена

В этом законе Кулон сформулировал действительную природу трения. Он указал, что трение представляет собой совокупность двух видов сцепления: зацепления, пропорционального нагрузке и не зависящего от площади (первое слагаемое в первой части закона трения), и сцепленности, связанной с площадью касания (А). Кулон был далек от понимания сцепленности как молекулярного взаимодействия. По обычаю того времени все явления, наблюдающиеся в природе, сводились к механическим. Кулон объяснял сцепленность между телами наличием "ворса", состоящего из материала трущихся тел.

В середине XIX века в учении о трении появляется тенденция постепенного отказа от взгляда на трение как на чисто механическое явление и объяснения его на основе атомно-молекулярных представлений о строении твердых тел. В 1834 году Дезаголье предложил при изучении трения тел принимать во внимание молекулярные силы. Однако эта мысль Дезаголье не была одобрена исследователями трения того времени и вскоре была забыта. Существенным толчком, повлиявшим на перемены в учении о трении, явилось развитие науки о молекулярном строении вещества и открытие закона сохранения энергии.

В 1901 году французский физик Бриллюэн опубликовал работу "Молекулярная теория трения твердых тел с гладкой поверхностью". Бриллюэн полагал, что поверхность твердого тела состоит из молекул, поэтому силы притяжения распределяются на ней периодически, образуя большое количество максимумов и минимумов. Для каждой свободной, а также слабо закрепленной молекулы существует множество положений устойчивого и неустойчивого равновесия. Каждое достаточно тесное сближение молекул трущихся тел вследствие взаимного их перемещения приводит к увеличению кинетической энергии этих молекул, которая затем переходит в тепловую. Он также указал, что рассеяние энергии при трении происходит аналогично рассеянию энергии магнитной стрелки, движущейся в неоднородном магнитном поле центров притяжения.

Дальнейшее развитие теории Бриллюэна было возможным лишь при исследовании взаимодействия идеально гладких поверхностей. Трудности экспериментального плана в то время не позволяли провести такие исследования, и поэтому теория Бриллюэна не получила своего дальнейшего развития.

Среди исследований в области трения, относящихся к этому же периоду, следует особенно отметить работы Гарди, сформулировавшего важное для дальнейшего развития теории положение о том, что реализация тангенциального усилия между трущимися телами является осуществимой лишь благодаря наличию дискретной структуры молекулярных полей твердых тел. Важное значение при трении твердых тел Гарди придавал поверхностным пленкам, находящимся на трущихся телах. По его мнению, взаимное скольжение контактирующих тел, лишенных поверхностных пленок, явилось бы невозможным в силу непременного сваривания тел.

Терцаги, исследуя трение твердых тел, в 1925 году установил, что при трении следует отличать кажущуюся (контурную) площадь контактирования от истинной (фактической) площади контакта. Истинная площадь контакта во много раз (по современным данным в 100...10000 раз) меньше кажущейся, и прямые ее измерения весьма затруднены. Площадь истинного контактирования между телами существенно возрастает по мере приложения к ним сжимающего усилия. По мнению Терцаги, причиной появления сопротивления относительному смещению твердых тел являются силы молекулярного притяжения в местах истинного контактирования трущихся поверхностей.

Первая попытка разработать теорию трения с учетом влияния сил молекулярного притяжения и отталкивания между атомами трущихся тел была предпринята Томлинсоном в 1929 году. Автор этой работы рассматривал процесс трения как совокупность двух элементарных явлений различного рода:

1) процесса разрыва молекулярных связей, сопровождающегося необходимыми потерями энергии;

2) процесса возникновения новых связей с проявлением сил отталкивания, уравновешивающих собой действие внешних сил.

При этом предполагалось, что при трении происходит только упругое деформирование трущихся тел. Для коэффициента трения Томлинсоном получено следующее выражение:

где W - работа разрыва одной молекулярной связи; L – расстояние между молекулами в кристаллической решетке; q - коэффициент, учитывающий хаотичность расположения молекул; R – элементарная сила отталкивания между молекулами.

где n - число молекулярных пар, воспринимающих давление N.

Применив закон Амонтона для пары молекул, Томлинсон получил выражение силы трения в следующем виде:

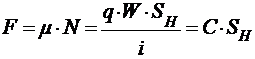где С - универсальная постоянная; S_н - номинальная площадь контакта, пропорциональная числу молекулярных пар, воспринимающих давление.

Использовав закон Амонтона для пары молекул в разработке своей теории, Томлинсон тем самым оставил открытым вопрос об обосновании на базе своей теории закона Амонтона и имеющих место отклонениях от него. Ошибки, допущенные Томлинсоном в процессе разработки своей теории трения, привели к противоречию с законом Амонтона и не допустили её дальнейшее распространение.

Строгая теория трения с учетом законов молекулярного взаимодействия твердых тел была разработана Б.В.Дерягиным. В основу теоретической схемы им была выбрана наглядная модель двух наложенных один на другой идеальных и одинаково ориентированных монокристаллов, имеющих шероховатость, обусловленную сферическими силовыми полями атомов поверхности, рассматриваемых автором теории как упругие шары.

Под влиянием нагрузки N (веса кристалла) шары верхнего тела входят во впадины между шарами нижнего тела (например, достигая положения точки А на рис. 3.1). Шары занимают энергетически более выгодное положение с минимумом потенциальной энергии и сближаются между собой до расстояний, при которых проявляются силы отталкивания между электронными оболочками.

Рис. 3.1. Механизм трения по Б.В.Дерягину:

АВС - траектория движения атома; N - нагрузка; А - сила притяжения;

F - внешняя сила; R - равнодействующая сил отталкивания

В качестве элементарного процесса трения рассматривается взаимодействие упругих шаров (атомных электронных оболочек), одни из которых подвижные, а другие - нет. Под действием внешней силы верхние шары начинают двигаться из потенциальной "ямы" (точка А) по поверхности нижних шаров, приобретая при этом потенциальную энергию. После преодоления некоторого потенциального барьера (точка В) они скачком переходят в соседнюю потенциальную "яму" (точка С), выделяя при этом тепловую энергию (как источник тепла, развивающийся при трении). По мнению Я.И.Френкеля, трение можно считать особым принципом мгновенного сброса избыточной кинетической энергии. В осуществлении этого процесса принимают участие только силы отталкивания между атомами.

Коэффициент трения при движении одного шара по другому определяется как отношение силы трения F к вертикальной нагрузке N и равняется тангенсу угла наклона в точке контактирования шаров, т.е.

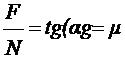При переходе от элементарного процесса трения к трению монокристалла в целом следует принимать во внимание и силы молекулярного притяжения между телами. В этом случае следует учитывать, что силы притяжения имеют больший радиус действия, чем силы отталкивания. Они медленно убывают с изменением расстояния от поверхности трения. Имеют более пологие изопотенциальные поверхности и меньше реагируют на атомарные неровности соприкасающихся тел. Силы молекулярного притяжения имеют свою равнодействующую, направленную почти вертикально, и тем самым увеличивают нормальную составляющую силы реакции. Тангенциальная же составляющая сил притяжения на практике близка к нулю. Образующийся при этом треугольник сил, действующий между телами в зоне контакта, имеет вид, представленный на рис. 3.1.

Исходя из треугольника сил, действующих между телами, тангенциальная и нормальная составляющие вектора равнодействующих сил отталкивания определяются следующим образом:

Полагая, что

имеем

Поскольку А_Т бывает величиной близкой к нулю, выражение представляется как

Принимая во внимание, что нормальная составляющая сил притяжения A_N равна произведению площади истинного контакта S на удельное давление контактирующих поверхностей трения Р_о, получают выражение

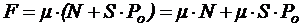Первое слагаемое в правой части формулы определяется силами отталкивания между телами, а второе слагаемое в правой части формулы вызвано силами притяжения. В тех случаях, когда роль адгезии между телами незначительна, двухчленный закон трения Б.В.Дерягина сводится к закону Амонтона

Развивая теорию трения Б. В. Дерягина для случая граничного тления твердых тел, когда на поверхностях трения находятся псевдокристаллические слои смазочного материала, А.С.Ахматов предлагает учитывать при трении помимо ван-дер-ваальсовых сил притяжения поверхностей трения твердых тел также и силы притяжения граничных смазочных слоев того же происхождения.

В этом случае закон трения Б.В.Дерягина приобретает следующий вид:

где Р_у - удельная сила притяжения между граничными слоями.

Строгая молекулярная теория трения Б.В.Дерягина, разработанная без учета кинетики молекулярного взаимодействия, является справедливой для абсолютно жестких и абсолютно гладких поверхностей. Расчет же конкретных величин трения по этим формулам сейчас затруднен, поскольку молекулярные характеристики для реальных твердых тел, к сожалению, в настоящее время еще остаются невыясненными.

Взгляды Терцаги на механизм трения нашли дальнейшее развитие в работе Бикермана и Райдила и особенно в работах Боудена и его школы. Согласно учению Боудена соприкосновение поверхностей происходит по выступам, где концентрируются очень большие давления. Под действием этих высоких давлений в точках контакта происходит пластическое течение материалов, при котором возникает значительная адгезия, и обе поверхности в местах контакта образуют как бы одно целое. Для металлов подобный процесс называют холодным свариванием (рис. 3.2). При относительном смещении тел происходит разрушение этих мостиков сварки, а затрачиваемая сила на срез мостиков становится близкой к силе трения. При движении одного тела по другому выступы более твердого тела будут «пропахивать» канавки в более мягком теле. Поэтому сила трения, по мнению ее авторов, представляется в следующем виде:

где F - сила трения; S_o - фактическая площадь контакта; t - сопротивление материала на срез; S - поперечное сечение дорожки трения (площадь поперечного профиля царапины); Р - удельное сопротивление вытеснения металла, приблизительно равно пределу текучести.

Боуден считает, что адгезия играет основную роль при трении тел, и трение нельзя рассматривать как поверхностное явление. В основе трения лежат объемные свойства материалов, такие, например, как соотношение твердостей трущихся тел, а при достаточно больших скоростях скольжения и соотношение температур плавления тел.

Рис. 3.2. Механизм трения по Ф.Боудену:

1 - область пластического течения; 2 - область упругой деформации;

F - сила трения; N - нормальная нагрузка

Ввиду пластического течения материала на выступах поверхности удельное давление тел остается постоянным и не превышает предела текучести. Нормальная нагрузка определяется как произведение площади фактического контакта на предел текучести материала, т.е.

С увеличением нормальной нагрузки удельное давление в зоне контакта, приблизительно равное пределу текучести, практически не меняется, а главным образом, происходит увеличение площади фактического контакта. Поэтому коэффициент трения согласно представлению Боудена выражается следующим образом:

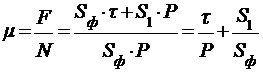Пренебрегая сопротивлением пластического оттеснения материала, считая его равным одной десятой и менее от сопротивления разрушения мостиков сварки, коэффициент трения Боуден выразил как отношение сопротивления на срез к пределу текучести более мягкого материала

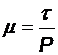Развиваемая Боуденом и Тейбором теория является, по существу, справедливой лишь для пластического контакта при условии, что трение происходит при постоянном напряжении.

Взглядов Боудена и Тейбора о трении тел придерживаются Эрнст и Мерчент. Рассматривая контакт трущихся тел как пластический, они предлагают выражение для определения коэффициента трения через отношение сопротивления материала на срез t к твердости Н

При трении реальных тел большую роль по формированию трения играют силы, возникающие при взаимном зацеплении выступов, всегда имеющихся на поверхностях трения. Поэтому помимо поверхностного взаимодействия ненасыщенных силовых полей соприкасающихся тел, на трение начинают оказывать влияние и объемные механические процессы. В деформационный процесс, сопровождающий трение, втягиваются массы материала (трущихся тел), значительно превышающие массу мономолекулярного поверхностного слоя.

По этому поводу П.А.Ребиндер и Г.И.Епифанов указывали, что в общем случае при трении протекают следующие процессы:

1) упругое и пластическое деформирование микронеровностей и пластическое течение в поверхностных слоях, приводящие к пластическому износу;

2) повторные микропластические деформации при периодических встречах микронеровностей, приводящие к установленному разрушению;

3) изменение механических и физических свойств поверхностных слоев металла вследствие глубокой пластической деформации.

Поэтому становится понятным то большое внимание, которое уделяется процессу деформирования (сдвигообразования) при трении в работах многих исследователей, таких как С.Я.Вейлер, И.В.Крагельский, Г.И.Епифанов, В.И.Лихтман, Д.М.Толстой и др.

Г.И.Епифанов считает, что в процессе трения пластически деформируются довольно толстые поверхностные слои. В опытах со сферическим ползуном и резцом с фаской им было установлено, что впереди движущегося индентора образуется застойная зона ОАБ (рис. 3.3) более слабого элемента фрикционной пары. За площадь среза принимается площадь внутренней границы ОБ застойной зоны ОАБ. Истинной пло\адью трения является суммарная площадь сдвига, образующегося в процессе трения.

Рис. 3.3. Механизм трения по Г.И.Епифанову

При исследовании трения и адгезии свежеобработанных полусферических образцов из меди, латуни, технического железа, магниевого сплава, скорлупы кокосового ореха и слоновой кости по олову и свинцу оказалось, что трение во всех опытах примерно одинаковое; адгезия для неметаллов большая, а для металлов - ничтожная. Это позволило автору считать, что адгезия не играет первостепенной роли в процессе формирования силы трения. Сила трения определяется в основном сопротивлением на сдвиг более мягкого материала. Для определения силы трения Г.И.Епифанов предлагает формулу следующего вида:

где t - прочность материала на сдвиг; S_C_Д - площадь сдвига.

В силу того, что прочность материала меняется с изменением сжимающего усилия между контактирующими телами, формула для определения силы трения преобразуется следующим образом.

Зависимость прочности материала на сдвиг от нормального давления принимается линейной

где t₀ - прочность материала на сдвиг при нормальном давлении, равном нулю; Р - нормальное давление; К = dt/dР - коэффициент пропорциональности между t и Р.

Коэффициент К находится из условия, когда отрицательное давление становится равным адгезии d_o, т.е. когда

Тогда

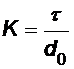После этого преобразования выражение для силы трения принимает вид

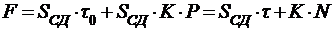где N - нормальная нагрузка (на рис. 3.3 не указана).

В случае смазки трущихся тел тонкими пленками Г.И.Епифанов предлагает выражать силу трения следующим образом:

где S_C_Д1 - площадь сдвига в пленке; S_C_Д2 - площадь поперечного сечения дорожки трения (пропахивания); t₁ - напряжение сдвига пленки; t₂ - сопротивление основного металла пластическому оттеснению.

Дальнейшее развитие атомно-молекулярной теории трения нашло отражение в работах В.А.Буфеева. В своих работах В.А.Буфеев вскрывает и исследует осцилляторный избирательно-резонансный механизм внешнего трения и предлагает весьма оригинальную макроскопическую теорию трения на базе термодинамики неравновесных процессов и теоремы Умова. Автор этой теоремы считает, что при трении твердых тел основными каналами диссипации энергии являются тепловой, электромагнитный и волновой. Данная теория трения представляет большой научный интерес и после проведения дополнительной экспериментальной проверки может найти широкое распространение при решении практических задач.

Значительным этапом развития в учении о трении было признание возможности наличия упругих деформаций контактирующих неровностей, выдвинутое впервые И.В.Крагельским еще в 1939-1941 гг. На основе этих представлений, с учетом современного развития учения о трении и двух основополагающих работ по внешнему трению И.В.Крагельского и А.В.Чичинадзе, была разработана молекулярно-механическая теория трения, которая получила наибольшее признание.

Молекулярно-механическая теория рассматривает двойственный процесс трения, заключающийся в преодолении адгезионных связей, возникающих на площадках фактического контакта, и в объемном деформировании внедрившимися неровностями тонкого поверхностного слоя. Трение определяется как результат взаимодействия всех выступов, имеющихся на реальном контакте. Оно зависит от микрогеометрии (высоты максимальной неровности, его радиуса закругления и показателей параболы, выражающей опорную поверхность), механических свойств (модуля упругости или твердости и прочности адгезионной связи) и внешних условий (нагрузки и скорости скольжения тел). Предполагается, что влияние температуры проявляется через изменение механических свойств трущихся тел.

В результате совместного рассмотрения задач теории упругости и пластичности И.В.Крагельским и Н.М.Михиным была получена следующая трехчленная формула, представляющая в общем случае величину граничного трения

где t₀ - прочность на срез адгезионной связи; Р_r - средние нормальные напряжения на контакте; b - пьезокоэффициент, характеризующий прочность на срез при увеличении нормального напряжения;

k - коэффициент, зависящий от вида контакта; h - величина внедрения; R - радиус неровности; a - коэффициент гистерезисных потерь.

Авторы молекулярно-механической теории трения утверждают, что она еще далека от своего завершения. На существующем уровне теория позволяет вычислять коэффициент трения по физико-механическим и микрогеометрическим характеристикам трущихся тел для случая трения покоя и при стационарных режимах трения, при условии слабо выраженных реологических свойств материала. Кроме того, она позволяет формулировать требования к физико-механическим характеристикам материалов, а также регламентировать технологию обработки. Становится ясным, что легче воздействовать на коэффициент трения в условиях упругого контакта, чем пластического. При упругом контакте это достигается путем регулирования давления и величины адгезионной составляющей. В условиях пластического контакта регулировать трение труднее. В связи с большим значением фактического давления желательно было бы иметь возможность воздействовать на пъезокоэффициент, но, к сожалению, он мало изучен. В условиях нестационарных режимов трения и при условии ярко выраженных реологических свойств материалов представляется возможным прогнозировать диапазон изменения коэффициента трения. Построение же аналитических зависимостей в этом случае представляет собой чрезвычайно сложную задачу. Большинство имеющихся в настоящее время теорий трения твердых тел не учитывают изменений, происходящих в контактной зоне в процессе трения (таких, как изменение шероховатости, механических свойств, зависящих от температуры трения и времени контакта, механико-химических процессов).

Обобщая существующее состояние учения о трении твердых тел, можно заключить, что трение - это сложный процесс взаимодействия между телами, в основе которого проявляются как механические, физико-химические, электрические, так и другие явления. Трение является результатом воздействия многих факторов, пока трудно поддающихся учету. Одним из сложных является учет механических и физических характеристик поверхностных слоев твердых тел,

меняющихся под влиянием физико-химических и механохимических факторов.

Пока еще не всегда удается количественно прогнозировать влияние на трение этих эффектов и приходится использовать результаты частных экспериментов для получения удельных характеристик, позволяющих рассчитывать процесс при других условиях. Следует всегда учитывать и то обстоятельство, что каждый из законов природы, в том числе и законы трения, имеет свои границы применения. Значение же разных подходов и соответствующих законов для объяснения природы фрикционного взаимодействия трущихся тел вооружает инженера и исследователя базовыми положениями и объяснениями процессов для решения производственных задач по совершенствованию работы узлов трения конкретных машин и механизмов.

Дата добавления: 2018-02-18; просмотров: 1762; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!