Структура металл-полупроводник

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

 

Макарчук М.В.

 

Методические указания на выполнение курсовой работы

по дисциплине “Физика полупроводников и диэлектриков”

 

Тамбов 2009

ЦЕЛЬ И ЗАДАЧИ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ

Целью выполнения ИЗ является:

– выяснение физической сущности явлений и процессов, лежащих в основе работы различных полупроводниковых структур и дискретных полупроводниковых приборов, а также элементов интегральных микросхем (ИМС);

– приобретение практических навыков расчета электрофизических характеристик полупроводниковых структур;

– ознакомление со значениями параметров полупроводниковых материалов и их размерностями;

– развитие навыков самостоятельной работы с научно-технической литературой.

ОСНОВНЫЕ СВЕДЕНИЯ О ФИЗИЧЕСКИХ ЯВЛЕНИЯХ И ПРОЦЕССАХ В ПОЛУПРОВОДНИКОВЫХ СТРУКТУРАХ

Вводные замечания

Интегральные микросхемы, являющиеся элементной базой микроэлектроники, предназначены для реализации подавляющего большинства аппаратурных функций. Их элементы, аналогичные обычным радиодеталям и приборам, выполнены и объединены внутри или на поверхности общей подложки, электрически соединены между собой и заключены в единый корпус. Все или часть элементов создаются в едином технологическом процессе с использованием групповых методов изготовления.

Элементы полупроводниковой интегральной микросхемы – диоды, транзисторы, резисторы, конденсаторы – представляют собой совокупность различных полупроводниковых структур.

К таким полупроводниковым структурам относятся: контакты металл-полупроводник, электронно-дырочные переходы, структуры металл-диэлектрик-полупроводник (МДП). Физические явления и процессы в таких полупроводниковых структурах хорошо изучены и детально рассмотрены в научной и технической литературе.

 

Основные понятия и уравнения твердотельной электроники

Температурный потенциал

j_Т=kT/q,

где k – постоянная Больцмана (k=1,38·10^-23Дж/К); T – абсолютная температура (при температуре T=300К температурный потенциал имеет значение j_Т =0,026В, или 26мВ), q – заряд электрона (q=1,6·10^-19Кл).

Закон действующих масс

n_i² = n·p

где n – концентрация электронов; p – концентрация дырок; n_i – концентрация носителей заряда в собственном полупроводнике. Закон справедлив в случае термодинамического равновесия как для собственных, так и для примесных полупроводников.

Потенциал, характеризующий уровень Ферми в полупроводнике, равен

j_F=j_i−j_bp или j_F=j_i+j_bn,

где j_i – потенциал, соответствующий середине запрещенной зоны полупроводника; j_bp=j_Тln(p/n_i), j_Fn=j_Тln(n/n_i) – объемные потенциалы. Таким образом, согласно данным выражениям, в собственных полупроводниках (n=p=n_i) уровень Ферми расположен в середине запрещенной зоны, в электронных полупроводниках (n>n_i) – в верхней половине, а в дырочных (р>n_i) – в нижней половине запрещенной зоны.

Уровень Ферми одинаков во всех частях равновесной системы, какой бы разнородной она ни была, т. е. j_F=const.

Закон полного тока в полупроводнике n-типа

j_n= q (n µ_nξ+D_n dn/dx),

 в полупроводнике р-типа

j_p= q (n µ_p ξ+D_p dp/dx),

где и dn/dx и dp/dx – градиент концентраций дырок и электронов; µ_p , µ_n – подвижности дырок и электронов соответственно; D_n и D_p – коэффициенты диффузии дырок и электронов; ξ – напряженность внешнего электрического поля.

Соотношение Эйнштейна, показывающее связь между коэффициентом диффузии и подвижностью носителей заряда,

 D_n=j_Т µ_n,

D_p=j_Т µ_p

в полупроводнике n- и p-типа соответственно.

Уравнение непрерывности для стационарных условий (∂_n/∂_t, ∂_p/∂_t=0), выражающее закон сохранения частиц,

,

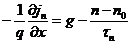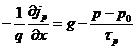
для полупроводников n- и p-типа, соответственно. Здесь n-n₀=∆n и р-р₀=∆р – избыточные (неравновесные) концентрации носителей заряда; g – скорость генерации носителей заряда под действием внешних факторов, например света; τ_n и τ_p – время жизни избыточных носителей заряда.

Время жизни неравновесных носителей заряда τ_n и τ_p равно промежутку времени, в течение которого их концентрация уменьшается в е раз.

Диффузионная длина носителей заряда соответствует расстоянию, которое они проходят за время жизни равна

,

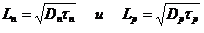где L_n и L_p – диффузионные длины электронов и дырок соответственно.

Уравнение Пуассона, позволяющее определить распределение потенциала в среде,

,

где j – потенциал; x – координата; ρ(x) – объемная плотность заряда; ε – диэлектрическая проницаемость среды, для полупроводника ε=ε_sε₀, где ε_s – относительная диэлектрическая проницаемость полупроводника, ε₀ – электрическая постоянная (ε₀=8,85·10^-12Ф/м).

Электронно-дырочный переход

2.3.1. Электронно-дырочный переход (p-n-переход) – это контакт двух полупроводников с различным типом проводимости. Электропроводность полупроводников p- и n-типов определяется следующими выражениями:

σ_p=qN_aµ_p,                                                           (1)

σ_n=qN_dµ_n,                                                           (2)

где σ_p, σ_n – электропроводность полупроводников p- и n-типов; N_a, N_d – концентрация акцепторов и доноров соответственно.

Удельное сопротивление материала p-типа

отсюда

 (3)

Аналогично концентрация доноров

(4)

При известных значениях N_a и N_d выражение для диффузионного потенциала (контактной разности потенциалов) может быть представлено в виде

(5)

2.3.2. Вольтамперная характеристика (ВАХ) идеального p-n - перехода может быть описана следующим выражением:

(6)

где I₀ – ток насыщения; U – приложенное напряжение. Ток насыщения I₀ определяется следующим выражением:

(7)

где A – площадь p-n-перехода.

Когда N_a»N_d, обратный ток насыщения определяется соотношением

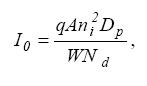(8)

где W – ширина p-n - перехода.

Аналогичное выражение можно получить и для случая, когда N_d»N_a

Зависимость тока насыщения от температуры определяется выражением

(9)

где j_g =E_g/q, E_g – ширина запрещенной зоны полупроводника; m – и η – постоянные, определяемые свойствами полупроводника. Для p-n - перехода, сформированного на германии,

Для p-n - перехода, сформированного на кремнии,

2.3.3. Определение дифференциального сопротивления p-n - перехода. Дифференцируя выражение (6) по напряжению и учитывая, что оно может быть представлено в виде

(10)

можно получить

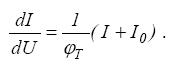
Если I»I₀, то

Следовательно, дифференциальное сопротивление

(11)

или

r=j_Т /I.                                                           (12)

При известном значении тока насыщения I₀  расчет величины тока удобно производить с помощью выражения (11).

2.3.4. Определение барьерной емкости p-n - перехода. Величина удельной емкости резкого p-n - перехода в общем случае рассчитывается по формуле

(13)

При этом толщина обедненного слоя (ширина p-n - перехода) определяется выражением

(14)

где

 

Для линейно-плавных переходов

(15)

где а – градиент концентрации примесей.

Толщина обедненного слоя в этом случае находится по формуле

(16)

2.3.5. Определение напряжения пробоя U_пр для несимметричного резкого p-n - перехода. Величина максимального значения напряженности электрического поля в p-n - переходе определяется по формуле

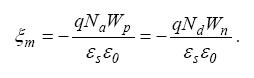(17)

При заданном значении ξ_m толщина обедненного слоя p-n - перехода может быть найдена как W=W_n+W_p, где

Напряжение пробоя для резкого несимметричного перехода

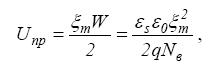(18)

где N_в– концентрация примеси в высокоомной области p-n - перехода.

Напряжение пробоя для линейно-плавных переходов

(19)

Оценка величины напряжения пробоя резкого p-n - перехода может быть сделана на основании приближенного выражения, справедливого для различных полупроводников:

(20)

Для линейно-плавных переходов величину напряжения пробоя можно оценить, используя соотношение

(21)

В выражениях (20), (21) размерность величин N_в  и а соответственно в см^-3 и см^-4, а ширины запрещенной зоны полупроводника E_g  в эВ.

 

Структура металл-полупроводник

2.4.1. Контакты на основе структуры металл-полупроводник обладают выпрямляющими свойствами в том случае, когда величина, равная разности работ выхода электронов из металла и полупроводника j_МП>0 для полупроводника n-типа проводимости и j_МП<0 для полупроводника p-типа проводимости. В этом случае j_МП обозначают j₀ и называют диффузионным потенциалом или контактной разностью потенциалов.

Согласно общей теории переноса носителей заряда в структурах металл-полупроводник (теории термоэлектронной эмиссии – диффузии) выражение для плотности тока имеет вид

(22)

Здесь   – скорость термоэлектронной рекомбинации носителей заряда на границе раздела структуры металл-полупроводник (А^* – эффективная постоянная Ричардсона, N_с – плотность электронных состояний в зоне проводимости полупроводника); ≈µξ₀ – скорость дрейфа носителей заряда в обедненной области полупроводника (ξ₀ – максимальное значение напряженности электрического поля в полупроводнике в области барьера Шоттки); j_в – высота барьера Шоттки, равная j_в =0,235j_M–0,352 для структуры металл-кремний n-типа проводимости, и j_в =E_g –(0,235j_M –0,352) для структуры металл-кремний p-типа проводимости.

Максимальное значение напряженности электрического поля в полупроводнике рассчитывается по формуле

ξ=2(j₀ -U)/W,                                           (23)

при условии U=0, где W – толщина обедненного слоя полупроводника, U – напряжение смещения, т.е. ξ₀=2j₀ /W.

В условиях равновесия W определяется выражением

(24)

где N – концентрация основных носителей заряда в полупроводнике.

Если  >> , то справедлива теория термоэлектронной эмиссии (теория Бете), и выражение для плотности тока (22) преобразуется к виду

(25)

В том случае, когда  << , определяющим является процесс диффузии (теория Шоттки), и плотность тока с достаточной точностью вычисляется по формуле

(26)

2.4.2. Для структуры металл-полупроводник распределение потенциала в области барьера Шоттки можно считать треугольным и аппроксимировать функцией

j_n (x)=j_n0 -ξx,                                           (27)

а распределение потенциальной энергии электрона

E_n (x)=E_n0 -qξx,                                          (28)

где j_n0 и E_n0 – высота потенциального барьера в В и эВ, соответственно, т.е. высота барьера Шоттки. Тогда подстановка (28) в выражение для расчета вероятности квантовомеханического туннельного перехода электрона с энергией Е сквозь потенциальный барьер произвольной формы

(29)

позволяет получить выражение для расчета вероятности туннелирования электрона сквозь барьер Шоттки в виде

(30)

В выражениях (29) и (30) m^* – эффективная масса электронов в полупроводнике, кг; ∆E=j_в–Е (Е – энергия электрона, туннелирующего из полупроводника в металл, эВ); ћ – постоянная Планка (ћ =1,05·10^-34Дж·с); ξ – напряженность электрического поля в полупроводнике, В/м, рассчитывается по формуле (23).

2.4.3. Барьерная емкость контакта металл-полупроводник определяется по формуле

(31)

где А – площадь контакта металл-полупроводник.

 

---

Дата добавления: 2018-02-15; просмотров: 636; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!