Математические и статистические функции
| Имя функции | Действие |
| КОРЕНЬ(число) | Возвращает значение квадратного корня |
| ПРОИЗВЕД(х1;х2;…) | Возвращает произведение аргументов |
| СТЕПЕНЬ(число;степень) | Возвращает результат возведения в степень |
| СУММ(х1;х2;…) | Суммирует аргументы |
| СУММКВ(х1;х2;…) | Возвращает сумму квадратов аргументов |
| СРЗНАЧ(х1;х2;…) | Подсчитывает среднее (арифметическое) своих аргументов |
| МАКС(х1;х2;…) | Возвращает максимальное значение из списка аргументов |
| МИН(х1;х2;…) | Возвращает минимальное значение из списка аргументов |
| СЧЕТ(х1;х2;…) | Подсчитывает количество чисел в списке аргументов |
| СЧЕТЕСЛИ(диапазон;условие) | Подсчитывает количество непустых ячеек в диапазоне, удовлетворяющих заданному условию |
| СУММЕСЛИ(диапазон;условие; диапазон_суммирования) | Суммирует ячейки специфированные заданным критерием |
| РАДИАНЫ(угол) | Преобразует градусы в радианы |
| ГРАДУСЫ(угол) | Преобразует радианы в градусы |
Логические функции
| Имя функции | Действие |
| ЕСЛИ(логическое_выражение; значение_истина; значение_ложь) | Вычисляет логическое выражение; если его значение истинно, возвращает значение истина, в противном случае возвращает значение ложь |
| ИСТИНА() | Возвращает логическое значение ИСТИНА |
| ЛОЖЬ() | Возвращает логическое значение ЛОЖЬ |
| НЕ(логическое_выражение) | Меняет значение своего аргумента на противоположное. Если значение выражения логическое_выражение истинно, функция возвращает значение ЛОЖЬ, и наоборот |
| И(х1;х2;...) | Возвращает значение ИСТИНА, если значения всех аргументов истинны; если хоть один из аргументов ложный, возвращает значение ЛОЖЬ |
| ИЛИ(х1;х2;...) | Возвращает значение ИСТИНА, если значение хотя бы одного аргумента истинно; если же все аргументы ложные, возвращает значение ЛОЖЬ |
|
|
|
Задача. Управление состоянием наполняемого резервуара.
Функция ЕСЛИ() б ячейке В7 проверяет, не превышает ли объем жидкости в резервуаре (В4) рабочий объем резервуара (В2).
Функция ЕСЛИ() в ячейке В8 проверяет, не превышает ли объем жидкости в резервуаре (В4) полную емкость резервуара (ВЗ).
Функция ЕСЛИ() в ячейке В15 сообщает оператору о необходимости перекрыть клапан как только объем жидкости залитой в резервуар, станет превышать емкость резервуара.

Работа с матричными объектами: векторы, матрицы и массивы
В Excel термином массив называется набор значений, расположенных в виде строк и столбцов и представляющих собой единую структуру. Матрицы и вектора в Excel рассматриваются как массивы.
Операции над матрицами выполняются по-разному:
- для сложения двух матриц и умножения матрицы на скаляр служат обычные
арифметические функции, производящие операции с содержимым ячеек;
|
|
|
- транспонирование, перемножение и обращение матриц выполняется с помощью
функций массива.
В Excel многие стандартные матричные операции реализованы как команды меню, однако транспонирование, обращение и умножение матриц можно выполнить и с помощью функций массива. Но следует учитывать, если матричные операции осуществляются без участия встроенных функций, то автоматический пересчет при изменении исходных данных невозможен.
Основные операции с матрицами
| Сложение двух матриц | Умножение матрицы на скаляр |
| Складывать матрицы можно только при условии, что они имеют одинаковый размер. Чтобы сложить две матрицы, нужно сложить все их соответствующие элементы. | Скаляр представляет собой константу. Чтобы умножить матрицу на скаляр, нужно умножить на скаляр каждый элемент этой матрицы. |

| 
|
Перемножение двух матриц
Две матрицы можно перемножить при условии, что количество столбцов первой матрицы равно количеству строк второй матрицы. Перед умножением следует указать, где будет находиться результирующая матрица (следует указывать реальный размер с правильным количеством ячеек; если размеры матриц заранее неизвестны, лучше выбрать слишком большой диапазон, чем слишком маленький). После указания местоположения новой матрицы, можно ввести функцию массива МУМНОЖ(матрица1;матрица2), выполняющую перемножение матриц, указывая диапазоны матриц с помощью мыши. Чтобы закончить ввод формулы следует нажать комбинацию клавиш Ctrl+Shift+Enter, тогда функция перемножения матриц будет введена во все ячейки матрицы-произведения.
|
|
|

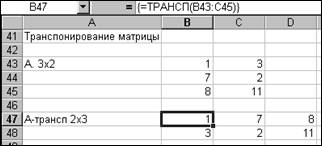
Транспонирование матриц с помощью функции ТРАНСП()
Необходимо:
- Ввести исходную матрицу.
- Указать диапазон ячеек соответствующего размера, куда нужно поместить результат.
- Ввести функцию массива ТРАНСП(матрица), указав с помощью мыши диапазон
ячеек, содержащих исходную матрицу.
- Ввод завершить комбинацией клавиш Ctrl+Shift+Enter.
Обращение матриц
Операция применима только к квадратным матрицам. Кроме того, она должна быть несингулярной.
Необходимо:
- Ввести исходную матрицу.
- Указать место для размещения обратной матрицы и ее правильный размер (он совпадает с размером исходной матрицы).
- Ввести функцию массива МОБР(матрица), указав с помощью мыши диапазон ячеек, содержащих исходную матрицу.
|
|
|
- Ввод завершить комбинацией клавиш Ctrl+Shift+Enter.

Вычисление детерминанта матрицы
Детерминант матрицы - это скалярная величина, которая определяется только для квадратных матриц. Часто используется для решения системы линейных уравнений, для определения сингулярности матрицы. Если детерминант матрицы равен 0, то система уравнений не имеет решения, а матрица сингулярная. Для вычисления детерминанта используется функция массива МОПРЕД(матрица).

Решение систем линейных уравнений
Одним из наиболее распространенных применений матричных операций является решение систем линейных алгебраических уравнений.
Процесс выглядит так:
1. Уравнения записываются в матричной форме (матрица коэффициентов, умноженная на вектор неизвестных, равняется известному вектору правой части уравнения).
2. Матрица коэффициентов обращается.
3. Правая и левая части уравнения умножаются на матрицу, обратную матрице коэффициентов.
В результате выполнения третьего шага получается вектор, компонентами которого будут искомые неизвестные. Естественно решение системы существует только тогда, когда матрица ее коэффициентов несингулярная.
Дана система уравнений с тремя неизвестными:



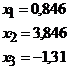

Задача. Найти по приведенной схеме неизвестные токи i1, i2 и i3.

Согласно закону Кирхгофа для напряжения алгебраическая сумма всех изменений напряжения в замкнутом контуре равна нулю.
Согласно закону Кирхгофа для тока алгебраическая сумма входящих и выходящих токов в любом разветвлении контура равна нулю.
Электродвижущая сила источника питания и значения сопротивлений приведены в таблице
| Е | 12 В |
| R1 | 30 Ом |
| R2 | 40 Ом |
| R3 | 50 Ом |
Закон Кирхгофа для токов в узле b:

Закон Кирхгофа применительно к левому и внешнему контурам цепи:

После выражения напряжения через токи и сопротивления, получается:

Получается система трех уравнений с тремя неизвестными i1, i2 и i3. Ее можно записать таким образом, чтобы в правых частях уравнений находились неизвестные, умноженные на соответствующие коэффициенты, а в левых - свободные члены:

В матричной форме ее можно записать:

После подстановки известных значений из таблицы:

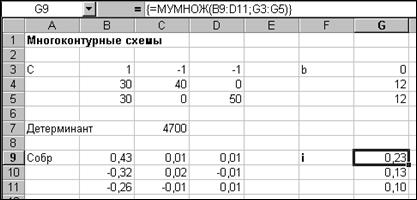
Вычисление детерминанта матрицы коэффициентов с помощью функции МОПРЕД0 свидетельствует о том, что решение системы уравнений существует, он не равен 0.
С помощью функции МОБР() находится обратная матрица системы.
С помощью функции МУМНОЖ() обращенная матрица умножается на вектор свободных членов. В результате получается решение системы уравнений, т.е. значения токов в контуре.
Использования функций поиска для поиска значений в таблицах и связи между таблицами
Электронные таблицы предоставляют возможность организации справочников (вспомогательных таблиц), позволяющих по коду некоторого объекта получить значения одного из нескольких сопоставляемых этому объекту параметров.
Справочник (вспомогательная таблица) представляет собой прямоугольный фрагмент, левая колонка или верхняя строка которого содержат коды, используемые для поиска нужных сведений. В первом случае справочник называется вертикальным, во втором - горизонтальным. Иногда справочник может быть частью той же таблицы, в которую добавляются найденные параметры. Справочники являются типичными примерами табличных документов, которые удобно реализовывать в среде электронных таблиц.
Для решения подобного рода задач используются функции ВПР (Вертикальный ПРосмотр) и ГПР (Горизонтальный ПРосмотр).
| Имя функции | Действие |
| ВПР(значение;массив;n;диапазон_просмотра) | Осуществляет поиск значения в первом столбце массива и возвращает значение из той же строки и n-го столбца |
| ГПР(значение;массив;n;диапазон_просмотра) | Осуществляет поиск значения в верхней строке массива и возвращает значение из того же столбца и n-ой строки |
Замечание. Если логический аргумент «диапазон_просмотра» имеет значение ЛОЖЬ, совпадение должно быть точным; если этот аргумент имеет значение ИСТИНА, из всех значений таблицы используется то, которое подходит лучше других.
Вызов функции с помощью Мастера функций, окно которого можно вызвать с помощью кнопки  на панели инструментов.
на панели инструментов.

В появившемся окне функции ВПР указываются ссылки на ячейки, в которых находятся значения для четырех параметров:
- Искомое_значение – то, что нужно найти в первом столбце справочника (марка самолета);
- Табл_массив – место расположения справочника, в котором осуществляется поиск;
- Номер_индекса_столбца – столбец справочника, в котором будет осуществляться поиск (назначение самолета);
- Диапазон_просмотра – логическая величина, определяющая, точно (ИСТИНА) или приближенно (ЛОЖЬ) должно производиться сравнение.
Следует обратить внимание, что ссылка на диапазон месторасположения справочника должна быть абсолютной.
Значит в ячейку Е15 будет введена формула =ВПР(A15;$A$3:$E$10;2;ИСТИНА)
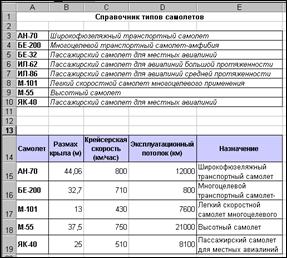
Пример использования функции ВПР при выборе назначения самолета по справочнику типов.
Дата добавления: 2018-02-15; просмотров: 755; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
