Отклоняющая сила вращения Земли

⇐ ПредыдущаяСтр 7 из 11Следующая ⇒

Мы уже знаем, что под ветром имеется в виду движение воздуха относительно земной поверхности, т. е. относительно системы координат, вращающейся вместе с Землей. В механике доказывается, что при движении любого тела во вращающейся системе координат возникает отклонение от первоначального направления движения относительно этой системы. Иными словами, тело, движущееся во вращающейся системе координат, получает относительно этой системы так называемое поворотное ускорение, или ускорение Кориолиса, направленное под прямым углом к скорости. Таким образом, поворотное ускорение не меняет величину скорости, а только меняет направление движения.

Будем под вращающейся системой координат разуметь поверхность вращающейся Земли, а под телом — воздух. На вращающейся Земле поворотное ускорение (здесь и дальше речь идет о его горизонтальной составляющей) направлено в северном полушарии вправо от скорости, в южном — влево.

Поворотное ускорение объясняется не тем, что есть какая-то внешняя сила, отклоняющая воздух от первоначального направления движения. На самом деле воздух стремится сохранить по инерции свое первоначальное направление движения, но не относительно вращающейся Земли, а относительно мирового пространства, относительно неподвижной системы координат. Система же координат, связанная с земной поверхностью, к которой относят ветер, поворачивается под движущимся воздухом в процессе суточного вращения Земли. Таким образом, не воздух отклоняется от первоначального направления относительно Земли, а Земля с ее параллелями и меридианами поворачивается под движущимся воздухом в противоположную сторону.

Поворотное ускорение на Земле имеет величину А =2ω sin φV, где ω есть угловая скорость вращения Земли, φ — географическая широта и V — скорость движения (ветра). Повторим, что речь идет только о горизонтальной составляющей поворотного ускорения.

Условно можно назвать поворотное ускорение отклоняющей силой вращения Земли (отнесенной к единице массы) или силой Кориолиса.

Отклоняющая сила вращения Земли обращается в нуль у экватора и имеет наибольшую величину на полюсе. Она также пропорциональна скорости ветра V и обращается в нуль при скорости, равной нулю. Если тело неподвижно, то никакого ускорения относительно Земли оно получить не может. Направлена отклоняющая сила под прямым углом к скорости, вправо в северном полушарии и влево в южном.

Найдем числовое значение величины 2ωV , например, для V= 10 м/сек. Так как полный оборот Земли вокруг оси продолжается 24 часа, т. е. 86400 сек, то угловая скорость вращения Земли ω = 2π : 86400 сек^-1 = 7,29*10^-5 сек^-1. Взяв удвоенное значение этой величины и умножить его на 10 м/сек, т. е. на10³ см/сек, получим ускорение, сообщаемое воздуху отклоняющей силой вращения Земли на полюсе при ветре 10 м/сек. Оно равно 1,5*10^-1 см/сек² и, таким образом, оказывается величиной того же порядка, что и ускорение, создаваемое в атмосфере барическими градиентами. Это очень важное обстоятельство: отклоняющая сила вращения Земли при движении воздуха может уравновесить силу барического градиента.

Геострофический ветер

Простейший вид движения воздуха, который можно представить теоретически, — это прямолинейное равномерное движение без трения. Такое движение при отклоняющей силе, отличной от нуля, называют геострофическим ветром.

При геострофическом ветре, кроме движущей силы градиента G = - 1/ρ*dp/dn на воздух действует еще отклоняющая сила вращения Земли A = 2ω*sinφ*V. Поскольку движение предполагается равномерным, обе силы уравновешиваются, т. е. равны по величине и направлены взаимно противоположно. Отклоняющая сила вращения Земли в северном полушарии направлена под прямым углом к скорости движения вправо. Отсюда следует, что сила градиента, равная ей по величине, должна быть направлена под прямым углом к скорости влево. А так как под прямым углом к градиенту лежит изобара, то это значит, что геострофический ветер дует вдоль изобар, оставляя низкое давление слева (рис. 75).

Рис. 75. Геострофический ветер. G — сила барического градиента, А — отклоняющая сила вращения Земли, V — скорость ветра.

В южном полушарии, где отклоняющая сила вращения Земли направлена влево, геострофичёский ветер должен дуть, оставляя низкое давление справа. Скорость геострофического ветра легко найти, написав условие равновесия действующих сил, т. е. приравняв их сумму нулю. Получим

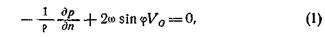
откуда, решив уравнение, найдем для скорости геострофического ветра

Это значит, что скорость геострофического ветра прямо пропорциональна величине самого барического градиента.Чем больше градиент, т. е. чем гуще проходят изобары, тем сильнее ветер.

Подставим в формулу (2) числовые значения для плотности воздуха при стандартных условиях давления и температуры на уровне моря и для угловой скорости вращения Земли; выразим скорость ветра в метрах в секунду, а барический градиент — в миллибарах на 100 км. Тогда получим формулу (2) в рабочем виде, удобном для определения скорости геострофического ветра (на уровне моря) по величине градиента:

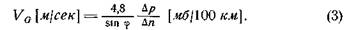
Например, при барическом градиенте 1 мб/100 км под широтой 55° получим V_G = 5,8 м/сек; при градиенте 2 мб/100 км — вдвое больше и т. д.

Ветер у земной поверхности всегда более или менее отличается от геострофического ветра и по скорости, и по направлению. Это происходит потому, что у земной поверхности достаточно велика сила трения, которая для геострофического ветра предполагается равной нулю. Но в свободной атмосфере, примерно начиная с 1000 м, действительной ветер уже очень близок к геострофическому, т. е. дует приблизительно по изобарам со скоростью, определяемой формулой (2). Сила трения на этой высоте и на более высоких уровнях так мала, что ею можно пренебречь. Кривизна траекторий воздуха в большинстве случаев там также мала, т. е. движение воздуха близко к прямолинейному. Наконец, хотя действительный ветер, как правило, не является вполне равномерным движением, все же ускорения в атмосфере обычно невелики.

В действительности ветер в свободной атмосфере все-таки отклоняется от изобар в ту или иную сторону, но на очень небольшой угол, порядка нескольких градусов. Скорость его также хотя и близка к скорости геострофического ветра, но не в точности равна ей. Тем не менее близость действительного ветра в свободной атмосфере к геострофическому ветру дает важную возможность с достаточным приближением определять скорость и направление действительного ветра на высотах по распределению давления.

Градиентный ветер

Если движение воздуха происходит без действия силы трения, но криволинейно, то это значит, что, кроме силы градиента и отклоняющей силы вращения Земли, появляется еще центробежная сила,выражающаяся как С = V²/r, где V — скорость, a r — радиус кривизны траектории движущегося воздуха. Направлена центробежная сила по радиусу кривизны траектории наружу, в сторону выпуклости траектории.

Тогда в случае равномерного движения должны уравновешиваться уже три силы, действующие на воздух, — градиента, отклоняющая и центробежная.

Допустим, что траектории движения являются окружностями (рис. 76, 77). Скорость в любой точке траектории направлена по касательной к окружности в этой точке. Отклоняющая сила направлена под прямым углом к скорости, стало быть, по радиусу окружности вправо (в северном полушарии). Центробежная сила также направлена по радиусу кривизны круговой траектории всегда в сторону ее выпуклости. Сила градиента должна уравновешивать геометрическую сумму этих двух сил и лежать на одной прямой с ними, т. е. на радиусе окружности. Это значит, что и барический градиент направлен под прямым углом к скорости. Поскольку под прямым углом к градиенту лежит касательная к изобаре, то, стало быть, ветер направлен по изобаре.

Такой теоретический случай равномерного движения воздуха по круговым траекториям без влияния трения называют градиентным ветром.Из изложенного видно, что траектории в случае градиентного ветра совпадают с изобарами. Градиентный ветер, так же как и геострофический, направлен по изобарам, в этом случае уже не прямолинейным, а круговым.

В понятие градиентного ветра часто включают также и геострофический ветер, как предельный случай градиентного ветра при радиусе кривизны изобар, равном бесконечности.

Дата добавления: 2018-02-15; просмотров: 2033; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!