Разложение по формуле Маклорена основных элементарных функций.

Стр 1 из 2Следующая ⇒

Последовательность { }.Пусть каждому натуральному числу n поставим в соответствие некоторое действительное число , тогда получим упорядоченное множество действительных чисел называемым последовательностью или числовой последовательностью. Предел последовательности.А называется пределом { } если для любого сколь угодно малого и положит. числа ε найдется число N завис/ от ε, такое что для всех номеров n>N(ε) выполняется нер-во (2) Свойства сходящихся последовательностей 1. Если последовательность { }имеет предел, то этот предел единственный. 2. Любая сходящаяся последовательность ограничена. (1) (3) Последовательность{ } бесконечно малая если ее предел равен нулю. Последовательность { }. бесконечно большая если ее предел равен бесконечности. { } - неограниченная последовательность если . Если последовательность бесконечно большая то она неограниченна, но не наоборот. (4) Теорема об ограниченности сходящейся последовательности. Последовательность, имеющая предел, - сходящаяся. Сход. посл. ограничена. (5) Монотонные последовательности. { }- называется монотонно возрастающей если последовательность строго возрастающая. { }- называется монотонно убывающей если последовательность строго убывающая. Теорема о пределе монотонной последовательности.Пусть последовательность { }- монотонно возрастает(убывает) и ограничена сверху(снизу) числом M и m, тогда она имеет конечный предел A причем Число e – это иррациональное число типа π. Рассмотрим { }., . Последовательность строго возрастает и ограничена e=2.7182819 – конечный предел. (6) Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа: Раскрытие неопределённостей типа :1.Выявление старшей степени переменной 2.Деление на эту переменную как числителя, так и знаменателя. Раскрытие неопределённостей типа :1.Разложение на множители числителя и знаменателя;2.Сокращение дроби.Для раскрытия неопределённостей типа иногда удобно применить следующее преобразование:Пусть и (7) Подпоследовательность , — возрастающая последовательность элементов множества натуральных чисел, получается из последовательности удалением конечного или счётного числа элементов. Теорема Больцано-Вейштрасса. Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. (8) Определения Sup и Inf множестваЧисло M назыв. точной верхней гранью не пустого, огр. сверху {X}, если выполн. сист. условий M = sup x Число m назыв. точной нижней гранью не пустого, огр. снизу {X}, если выполн. сист. условий m=infx (9) Теорема о вложенных отрезках.Последовательность называется последовательностью вложенных отрезков, если выполняется система из двух условий, последовательность имеет единственную точку c принадлежащую всем отрезкам. (10) Определение предела функции. Aназывается пределом f(x) при если: 1) f(x) определена в некоторой окрестности x0 за исключением самой этой точки. 2) . По Коши.Aназывается пределом f(x) при если: 1) f(x) определена в некоторой окрестности x0 за исключением самой этой точки. 2) найдется . По Гейне.Aназывается пределом f(x) при если для любой числовой последовательности xn сходящейся к точке x0, следует что соответствующая ей функция сходится к A . Эквивалентность определения по Гейне и Коши.Если существует предел функции определенный по Коши, отсюда следует, что для любой последовательности сходящейся к ,следует что соответствующая послед-сть сходится к числу A . (11) Свойства пределов числовых функций Пусть даны функции и . Одна и та же функция в одной и той же точке может иметь только один предел. Предел суммы равен сумме пределов: Предел разности равен разности пределов: Предел произведения равен произведению пределов: Предел частного равен частному пределов.

Бесконечно малые и бесконечно большие функции. Сравнимость. Эквивалентность

Б.Б.Ф. – это ф-я y=f(x) при , если для любого числа M > 0 сущ. Число , что для всех x, удовлетворяющих неравенству , выполняется неравенство 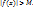Записывают . Например ф-я явл. Б.Б.Ф. при .

Б.М.Ф. – это ф-я y=f(x) при , если .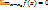

Сравнимость: Две б.м.ф. сравнив. между собой с помощью их отношения. Пусть есть б.м.ф. т.е.
Если , то α и β назыв. беск. мал. одного порядка.
1) Если , то α назыв. беск. мал. более выс. порядка, чем β.
2) Если , то α назыв. беск. мал. более низкого порядка, чем β.
3) Если 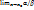не сущ., то α и β назыв. несравнимыми беск. мал.
Таковы же правила сравнения б.м.ф. при
Важнейшие эквивалентности, которые исп. при вычислении пределов:
1) sinx ~ х при х→0;                    8) ln(1+х) ~ х (х→0);
2) tgx ~ х (х→0);                          9) log_a(l+х) ~ х*log_aе (х→0);
3) arcsinх ~ х (х→0);                   10) (1+х)^k-1 ~ k*х, k>0 (х→0);
4) arctgx ~ х (х→0);
5) 1-cosx ~ x²/2 (х→0);
6) е^х-1 ~ х (х→0);
7) α^х-1 ~ х*ln(a) (х→0);

(13) Первый замечательный предел.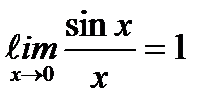

Второй замечательный предел. .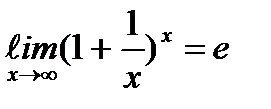

(14) Непрерывность функции в точке. 1) f(x) называется непрерывной в точке , если она определена в некоторой окрестности точки , в том числе и в самой этой точке и существует Непрерывность на интервале.f(x) непрерывна на интервале (a,b) если она непрерывна в каждой точке интервала. Непрерывность на отрезке.f(x) непрерывна на отрезке [a,b] если она непрерывна на интервале и (a,b) выполняется система

(15) Классификация точек разрыва. Если f(x) определена в некоторой окрестности и не является в этой точке непрерывной, тогда - точка разрыва f(x) 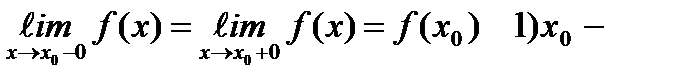называется точкой устранимого разрыва f(x) если существует конечный предел точка разрыва 1-ого рода если существует предел слева и справа, оба конечны и не равны друг другу точка разрыва 1-ого рода.
3) - точка разрыва 2-ого рода если хотя бы один из пределов слева и справа равен бесконечности или не существует.

(16) Производная.Если, то он называется производной от f(x) в точке x . Геометрический смысл производной. в любой точке x равна tg угла наклона касательной к графику f(x) в точке с абсциссой x к положительному направлению оси Ox. Угол между кривыми. Пусть графики функций пересекаются в точке тогда углом между кривыми в точке с абсциссой

(17) Ур-е касательной и нормали

Пусть даны кривая y = f(x) и точка M (x₁ ; y₁) на ней. Требуется составить уравнения касательной и нормали (смотри рисунок).
Как известно, угловой коэффициент k касательной к кривой y = f(x) в точке M (x₁ ; y₁) равен значению f '(x₁) производной y' = f '(x) при x = x₁/ Следовательно, уравнение касательной можно записать в виде уравнения прямой, проходящей через данную точку в данном направлении, т.е. в виде

y - y₁ = f '(x₁)(x - x₁)

Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. поэтому ее угловой коэффициент равен , а уравнение записывается в виде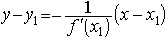

(18)Таблица производных

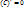
2) (хⁿ)=n•хⁿ^-1

3) (e^x)'=e^x

4) (a^х)'=a^хInа

6) (sinx)'=cosx.

7) (cosх)'=-sinx

10)

11)

12)

13)

(19) Св-ва ф-и имеющую произв.

Теорема: Если f(x) имеет произв. в точке х, то в этой точке она непрерывна. Обратное не верно.

(20) Производные суммы, разности, произведения и частного.

Пусть существуют производные и , тогда существуют производные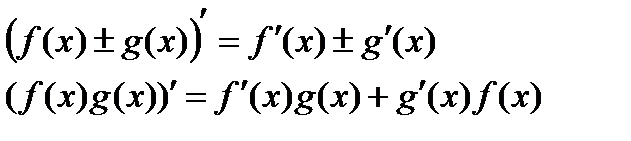

(21)Теорема о производной сложной функции. Пусть 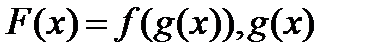имеет производную в точке x, а имеет производную в точке

(22) Теорема о производной параметрический заданной функции. считается заданной параметрически если имеет место система. Пусть f(x) задана параметрически имеют производные в точке t₀ предположим, что .

(23) Логарифмическая производная.В некоторых случаях применяют предварительно логарифмирование функции называется логарифмической производной. Рассмотрим функцию 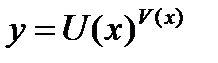применим основное логарифмическое тождество.

Теорема о производной обратной функции.Пусть 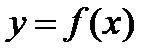имеет обратную функцию , тогда . Док-во. Пусть , с другой стороны

(24) Производная неявно заданной функции.

Если независимая переменная x и функция y связаны уравнением вида F(x,y) = 0 , которое не разрешено относительно y, то функция y называется неявной функцией переменной x. Достаточно продифф. это ур-е по х, рассматривая при этом у как ф-ю от x.

(25)Экстремум функции.Точка - точка локального максимума f(x) если , такая что , аналогично точка называется точкой локального минимума если . Точки локального максимума и минимума в совокупности называются точками локального экстремума.

(26)Теорема Ферма. -точка локального экстремума f(x) и существует , тогда , теорема Ферма будучи необходимым условием экстремума говорит о том что экстремум функции нужно искать в точках где производная равна нулю остальные рассмотрению не подлежат, однако теорема Ферма не охватывает случаи, когда экстремум есть, а производная не существует, поэтому такие точки, в которых производной не существует также нужно исследовать на экстремум.

Теорема Ролля.Пусть функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b) и принимает на концах отрезка одинаковые значения тогда существует . Если f(x) непрерывна на [a,b] и достигает на нем max(min) значения в некоторой внутренней точке , то точка
c-точка лок. max(min). Если max(min) значение функции достигается в одной из концевых точек [a,b] то эта точка не является точкой локального max(min), т.к. функция f(x) неопределенна в полной окрестности этой точки. Теорема Роля сохраняет силу и для интервала, но при выполнении дополнительного условия теорема Роля теряет силу если хотя бы в одной точке не существует производной.

Теорема Лагранжа (о среднем). Пусть f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b) тогда найдется 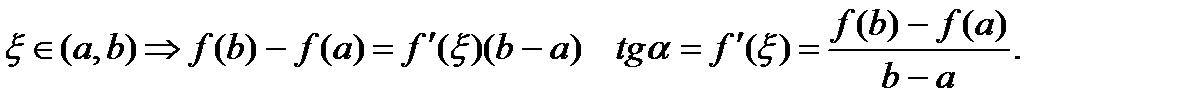Геометрический смысл. Существует в которой существует касательная параллельная секущей соединяющей точки графика. Следствие 1. Если для любых x из промежутка (a,b) существует . Следствие 2. Пусть f(x) имеет производную и для .

Теорема Коши.Пусть функции f(x) и g(x) непрерывны на отрезке [a,b] и дифференцируемы на интервале (a,b), , для любого , тогда .

(27) Правило Лопиталя (Бернулли). Теорема 1. Пусть f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки за исключением самой точки в рассматриваемой окрестности, тогда если существует и они равны.

Теорема 2 Пусть f(x) и g(x) определены и дифф-емы в некоторой окрестности точки за исключением , в рассматриваемой окрестности, тогда если , то они равны. Таким образом правило Лопиталя опред/ для
Замечания: 1) Если предел справа не существует , то предел слева может существовать.

2) Если, то теоремы 1 и 2 сохраняют силу. 3) Если представляет собой неопределенность вида и удов/ условиям теорем 1 и 2, то если сущ. и они равны.

3)Лопиталя можно применять циклично, но на каждом шаге проверять существует ли он.

(28)Формула Тейлора. Теорема. f(x) в некоторой окрестности имеет непрерывные производные до n+1 порядка включительно, тогда f(x) можно представить в виде - остаточный член. Остаточный член в форме Лагранжа

(29) Формула Маклорена. Если в формуле Тейлора положить , то это и будет формула. величину можно оценить если известно огранич. [a,b] , запишем разделим обе части на при правая стремится к нулю, тогда стремится и левая но она же равна по определению 0, след. что .

Разложение по формуле Маклорена основных элементарных функций.

(30)Достаточные условия сущ. экстремума. 1) существует в точке , и равна 0 называется стационарной. Экстремумы функции возможны где производная существует и равна нулю

(т. Ферма), а также формы где не существует причем всегда внутренняя точка. 2) , т.е. при переходе через точку слева направо производная меняет знак с - на + тогда имеет локальный минимум 3) Если на всей окрестности, то есть при переходе через точку , производная не меняет знак, то в точке экстремума нет.

(31)Выпуклость ф- и, точки перегиба: определения и геометрический смысл. 1)Точка - точка перегиба кривой , если при переходе x через точку кривой переходит с одной стороны наклонной на другую. 2) Функция непрерывна на некотором промежутке (a,b) называется выпуклой книзу(кверху), если для любых точек выполняется неравенство для . Для любых и таких, что их сумма равна 1 3)Точка -точка перегиба кривой, если она отделяет участок на котором функция выпукла книзу(кверху) от участка где она выпукла кверху(книзу).

(32)Асимптоты графика функции. 1)Прямая x=a называется асимптотой графика функции если хотя бы один из пределов
2)Пусть определена для любых , тогда называется наклонной асимптотой графика функции при , если представляется в виде где при .

(33)Схема исследования функции.
1)Найти область определения и область значений
2)Приравнять и найти т. Пересечения с Ox
3)Исследовать на четность, нечетность, периодичность.
4)Исследовать на границах области определения
5)Исследовать на непрерывность, найти точки разрыва, пределы слева и справа и определить классификацию точек разрыва.

6)Найти производную , найти стационарные точки и точки где производная не существует. Найти точки экстремума и локальные экстремумы и указать промежутки монотонности.

7) . Определить промежутки выпуклости вверх, вниз и точки перегиба.
8)Найти асимптоты.

(34) Неопред. инт. опред. и св-ва.

Определение.Совокупность всех первообразных функции f(x) называется неопределенным интеграломот f(x) и обозначается . f(x) называется подынтегральной функцией, а f(x)dx -подынтегральным выражением.Таким образом, окончательно .

Дата добавления: 2018-02-15; просмотров: 536; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!