Присоединенные функции Лежандра
Глава 1. Сферические функции
Сферические функции были введены в связи с изучением решений уравнения Лапласа, и в частности с теорией потенциала. В §1 мы рассматриваем полиномы Лежандра, которые используются затем для построения шаровых и сферических функций в §2. Сферические функции являются весьма мощным аппаратом для решения многих задач математической физики.
Полиномы Лежандра
Производящая функция и полиномы Лежандра
Полиномы Лежандра тесно связаны с фундаментальным решением уравнения Лапласа  , где R – расстояние от точки М до фиксированной точки М0. Пусть r и r0 – радиусы векторы точек М и М0, а
, где R – расстояние от точки М до фиксированной точки М0. Пусть r и r0 – радиусы векторы точек М и М0, а  - угол между ними. Очевидно можно записать
- угол между ними. Очевидно можно записать
 (1)
(1)




при 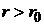


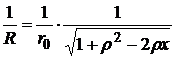
при 


 ,
, 
производящая функция полиномов Лежандра.
Разложим функцию  в ряд по степеням
в ряд по степеням  :
:
 (2)
(2)
 ,
, 
Коэффициенты  в разложение (2) являются полиномами n-й степени и называются полиномами Лежандра.
в разложение (2) являются полиномами n-й степени и называются полиномами Лежандра.
В силу теоремы Коши из формулы (2) следует, что
 (3)
(3)
от  ,
,  (перейдем в комплексную плоскость). Используя интегральную формулу Коши и производную
(перейдем в комплексную плоскость). Используя интегральную формулу Коши и производную
 (4)
(4)
Полагая  , находим
, находим  ,
,  ,
,
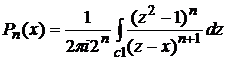 , (5)
, (5)
где С1- любой контур, окружающий точку x=z. Подинтегральная функция имеет особенность, а именно полюс (n+1) порядка.
 ,
,

 . (6)
. (6)
|
|
|
Из формулы (6) непосредственно видно что:
1. Получили полином степени n;
2. Полином содержит степени x той же четности, что и номер n, так что
 . (7)
. (7)
Просмотрим граничные условия:
x=1,
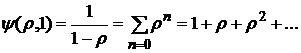 ,
,
 ,
,
Формула (6) называется дифференциальной формулой для полиномов Лежандра или формулой Родрига. С учетом (7)
 .
.

 ,
,
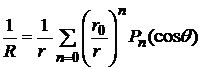
 . (8)
. (8)
Рекуррентные формулы
Используя производящую функцию
 ,
,
и найдем частные производные по  и по
и по  :
:
 ,
,
 , (9)
, (9)
 , (9а)
, (9а)
Запишем левую часть формулы (9) в виде степенного ряда относительно  , подставив в нее ряд (3) для
, подставив в нее ряд (3) для 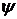 и ряд
и ряд
 .
.
 . (10)
. (10)
 ,
,
Возьмем производную по  :
:
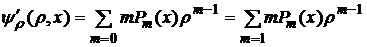

m-1=n 1-a m+1=n 2-a m=1 3-a m=0 4-ая m+1=n 5-ая
m=n+1 сумма m=n-1 сумма n=m сумма m=n сумма m=n-1 сумма
n=0,1,2 n=2,3,4, n=1,2 n=0 n=1,2

Запишем коэффициенты при  0,
0,  1,…,
1,…,  n.
n.


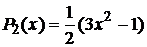
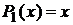
 , где n ≥2. (11)
, где n ≥2. (11)
Таким образом, выражение (11) представляет собой рекуррентное соотношение.
Домножим (9) на  ,(10) на (
,(10) на (  ) и вычтем
) и вычтем
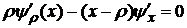
 , (12)
, (12)
 ,
,
При любом m получаем m+1=n, n=1
 , (13)
, (13)
|
|
|
рекуррентная формула
 , (14)
, (14)
Продифференцируем по x соотношение (11):
 , (15)
, (15)
Уравнение Лежандра
Найдем дифференциальное уравнение, решением которого является 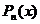 . Для этого исключим Pn-1 и Pn-1 из (14) и (15). Подставляем (14) в (15):
. Для этого исключим Pn-1 и Pn-1 из (14) и (15). Подставляем (14) в (15):
 ,
,
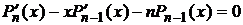 ,
,
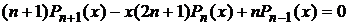 ,
,
 .
.
Продифференцируем:
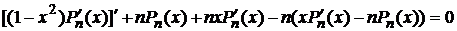 .
.
 . (16)
. (16)
Соотношение (16) представляет собой уравнения Лежандра. Тем самым доказано что полиномы Лежандра являются собственными функциями, соответствующими собственным значениям  , следующей задачи.
, следующей задачи.
Найти такие значения λ, для которых на отрезке  существуют нетривиальное решение уравнение Лежандра
существуют нетривиальное решение уравнение Лежандра
 , (17)
, (17)
с областью  с условием
с условием 
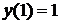 . Таким образом нетривиальное решение существует при
. Таким образом нетривиальное решение существует при 
 .
.
Ортогональность полиномов Лежандра и их норма
Докажем что полиномам Лежандра различных порядков ортогональны на отрезке  . Согласно общей теореме присоединенные функции
. Согласно общей теореме присоединенные функции  образуют ортогональную систему. Вычислим норму
образуют ортогональную систему. Вычислим норму  присоединенных функций. Попутно будет доказана их ортогональность.
присоединенных функций. Попутно будет доказана их ортогональность.
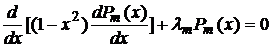 , (1)
, (1)
 , (2)
, (2)
где  ,
,  . Домножим (1) на
. Домножим (1) на  (x), а (2) на
(x), а (2) на  (x), а затем вычтем (1) из (2):
(x), а затем вычтем (1) из (2):
 ,
,
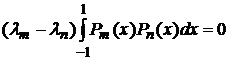 , (3)
, (3)
|
|
|
Доказать ортогональность если  . Если
. Если  , то полиномы Лежандра разных порядков ортогональны между собой:
, то полиномы Лежандра разных порядков ортогональны между собой:
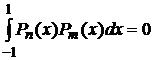
 . (4)
. (4)
Норма полиномов Лежандра
Вычислим норму полиномов Лежандра 
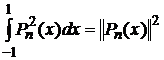
 (5)
(5)
Применим рекуррентную формулу (11) (§1.1) дважды: сначала выразим из нее (предварительно заменив в (11) n+1 на n)  через
через  и
и  , а затем
, а затем  через
через  и
и  . Учитывая ортогональность полиномов
. Учитывая ортогональность полиномов  ,
,  ,
,  , получим:
, получим:

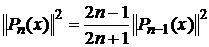 (6)
(6)
Рекуррентная формула для нормы:
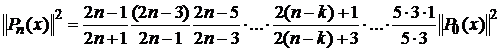

 (7)
(7)
Полиномы Лежандра образуют замкнутую систему функций. Поэтому произвольная функция может быть разложена в ряд
 ,
,
который домножим на  и проинтегрируем:
и проинтегрируем:

 .
.
Система ортогональных функций называют замкнутой если не существует непрерывных функции тождественно равных 0 и ортогональных ко всем функциям системы.
Система ортогональных функций  называется полной в (a,b) если любую непрерывную функцию можно аппроксимировать с любой степенью точности при помощи линейной комбинации
называется полной в (a,b) если любую непрерывную функцию можно аппроксимировать с любой степенью точности при помощи линейной комбинации 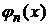 .
.



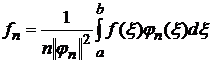

Замкнутость есть условие полноты, а полнота есть следствие замкнутости.
Упражнения
1. Получить полиномы Лежандра, используя производящую функцию, для n=0,1,2.
|
|
|
2. Получить полиномы Лежандра, используя формулу Родрига, для n=0,1,2,3,4,5.
3. Получить полиномы Лежандра, используя рекуррентную формулу для коэффициентов, для n=0,1,2,3,4,5,6.
Ответ:

4. Построить и исследовать (найти точки перегибов, максимумов и минимумов) полиномов Лежандра для n=0,1,2,3,4,5.
5. Получить присоединенные функции Лежандра для n, m=0,1,2,3,4. Выразить данные функции через тригонометрические функции.
6. Получить сферические функции для l=0,1,2.
7. Показать, что сферические функции ортонормированны. Ограничиться l=0,1.
8. Выполнить визуализацию сферических функций.
Ответ:


Присоединенные функции Лежандра
Присоединенные функции
Рассмотрим следующую задачу:
Найдем собственные значения и собственные функции следующего уравнения
 (1)
(1)
-1<x<1 при условии ограниченности
 (2)
(2)
Будем искать решение в виде:
 (3)
(3)
Подставим (3) в (1), найдем
 ,
,
 ,
,

 . (4)
. (4)
Это же уравнение получается для производной  решения уравнения Лежандра (17) из §1, если продифференцировать m раз.
решения уравнения Лежандра (17) из §1, если продифференцировать m раз.
 , (4а)
, (4а)
 ,
,
Продифференцируем соотношение (4) n раз, тогда получим
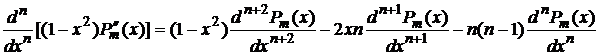 ,
,
 ,(5)
,(5)
 . (6)
. (6)
Нетривиальное и ограниченное решение  решении уравнения Лежандра существует при
решении уравнения Лежандра существует при  , где m>0. Решение Соотношение (6) является решением уравнения (3)
, где m>0. Решение Соотношение (6) является решением уравнения (3)
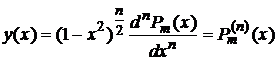 ,
,
есть собственная функция исходной задачи (1) для собственных значений  , где m-целые числа (7).
, где m-целые числа (7).  - присоединенная функция Лежандра
- присоединенная функция Лежандра
 ,
,
Если n=0, то

 при
при  .
.
Норма присоединенной функции
Согласно общей теоремы присоединенные функции образуют ортогональную систему. Вычислим норму  и докажем ортогональность
и докажем ортогональность
 (8)
(8)
Уменьшим n на 1:
 (9)
(9)
 , (10)
, (10)
Введем обозначение:

Подстановка обращается в нуль, а интеграл в силу (8) и (7) преобразуется к виду
 ,
,
 , (11)
, (11)
 , (12)
, (12)


Нетрудно показать, что
 ,
,
 .
.
Сферические функции
Сферические функции
Сферические функции проще всего могут быть введены при решении уравнения Лапласа для шаровой области методом разделения переменных. Разделение переменных в уравнении Лапласа в сферических координатах:
 ,
,
 ,
,
где 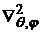 - угловая часть оператора Лапласа в сферических координатах.
- угловая часть оператора Лапласа в сферических координатах.
 , (1)
, (1)
 . (2)
. (2)
Решение уравнения Лапласа:
 , (3)
, (3)
 ,
,
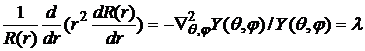 . (4)
. (4)
Для определения  получаем уравнения
получаем уравнения
 , (5)
, (5)
где 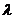 - константа разделения.
- константа разделения.

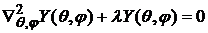 , (6)
, (6)
Для определения R(r) получаем уравнение Эйлера:
 ,
,
 . (6а)
. (6а)
Следствия:
1. Функция  должна быть ограничена на сфере любого радиуса.
должна быть ограничена на сфере любого радиуса.
2. Функция  должна в точках
должна в точках  ,
,  , а также
, а также  .
.
Ограниченное решение уравнения (6) обладающее непрерывными производными до второго порядка называются сферическими функциями. Решение задачи для  ищем также методом разделения переменных, полагая
ищем также методом разделения переменных, полагая
 . (7)
. (7)
 ,
,
Умножим на  и поделим на (7)
и поделим на (7)
 ,
,
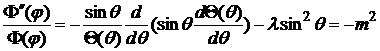 , (8)
, (8)
где m-константа разделения.
 (9)
(9)
Задача для  имеет решение лишь при целом m, и линейно независимыми решениями являются функции
имеет решение лишь при целом m, и линейно независимыми решениями являются функции  и
и 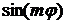 .
.
Функция  определяется из уравнения
определяется из уравнения
 , (10)
, (10)
 (11)
(11)

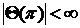 (12)
(12)
 , (13)
, (13)
решение (9).
Если потребовать выполнение условия (11)
 ,
,
 m- любое число m=0,1,-1,2,-2…
m- любое число m=0,1,-1,2,-2…
 ,
,

 m=0,1,-1… (14)
m=0,1,-1… (14)
Выберем новую переменную  и обозначая
и обозначая  , получаем для
, получаем для  уравнение присоединенных функций (15)
уравнение присоединенных функций (15)


подставляем все в (10)

 . (15)
. (15)
Полученное уравнение является уравнением для присоединенных функций Лежандра

Потребуем чтобы функции  были нормированными
были нормированными


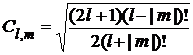 (16)
(16)
 , (17)
, (17)
где 
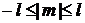 .
.
 (18)
(18)
Уравнение (6) имеет решение (18) при собственных значениях  . Найдем несколько сферических функций
. Найдем несколько сферических функций


Легко проверить, что сферические функции является ортонормированными, т.е. справедливо:




Кроме сферических функций используется понятие сферической гармоники которые определяется следующим образом:
число различных сферических функций n-го порядка  равно 2n+1. Линейная комбинация этих (2n+1) сферических функций
равно 2n+1. Линейная комбинация этих (2n+1) сферических функций
 ,
,
Решение уравнения имеет вид:

Специфика заключается в нахождении радиальной части волновой функции R(r).
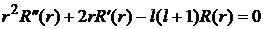 ,
,

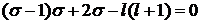 ,
,
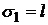
 ,
,

 .
.
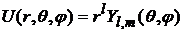 ,
,
есть внутренняя краевая задача, а

есть внешняя краевая задача.
Дата добавления: 2018-02-15; просмотров: 3429; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
