ТЕМЫ КУРСОВЫХ РАБОТ по АРЭС для гр. ЭЭБЗ-06-14
Диагностирование цифровых устройств
При диагностировании цифровых устройств в качестве тестовых воздействий, как правило, используют логические сигналы (входной набор), которые подаются на внешние входы устройства, а в качестве реакций — внешние выходные сигналы. Большинство отказов цифровых устройств проявляется в том, что некоторые выходные или внутренние переменные фиксируются и принимают значение константы: 0 или 1. Отказы устройства обусловлены отказами элементов или нарушениями их связей.
Полагая, что отказы элементов существенно преобладают и что у них наиболее вероятны одинаковые неисправности, получим общее число различных неисправностей:
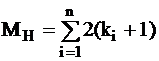 ,
,
где ki — число входов i-го элемента схемы;
n — число элементов в схеме.
Формализация построения алгоритмов (диагностики неисправности объекта) предполагает наличие формального описания объекта и его поведения в исправном и неисправном состояниях. Такое описание в аналитической, графической, табличной, векторной или другой форме называют математической моделью объекта. Наиболее удобной для диагностики формой моделей является таблица функций неисправностей ТФН. Строки ТФН соответствуют допустимым элементарным проверкам, а столбцы — техническим состояниям объекта. В клетке таблицы, находящейся на пересечении i-й строки и j-гo столбца, ставят результат 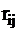 элементарной проверки объекта, находящегося в состоянии
элементарной проверки объекта, находящегося в состоянии 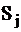 . С помощью ТФН можно разрабатывать оптимальные алгоритмы диагностирования, а также проводить анализ результатов проверок и определять техническое состояние объекта.
. С помощью ТФН можно разрабатывать оптимальные алгоритмы диагностирования, а также проводить анализ результатов проверок и определять техническое состояние объекта.
Обозначим неисправность i-го элемента схемы 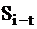 если сигнал на выходе i-го элемента (0 или 1) фиксирован значением t, и
если сигнал на выходе i-го элемента (0 или 1) фиксирован значением t, и  , если сигнал на j-м входе i-гo элемента (0 или 1) фиксирован значением t, где
, если сигнал на j-м входе i-гo элемента (0 или 1) фиксирован значением t, где 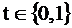 (t принадлежит множеству 0, 1).
(t принадлежит множеству 0, 1).
Через 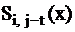 ‑ обозначим функцию, реализуемую схемой при наличии в ней неисправности
‑ обозначим функцию, реализуемую схемой при наличии в ней неисправности  . Эта неисправность проверяется и обнаруживается на входном наборе «е» если
. Эта неисправность проверяется и обнаруживается на входном наборе «е» если 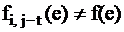 .
.
Таким образом, строки ТФН, описывающей логическую схему, сопоставляются с входными наборами «е»: столбцы — с функциями  , а в клетках ТФН записываются значения функций при соответствующих наборах. Ниже приведена ТФН для трёхвходного элемента И-НЕ (табл. 1).
, а в клетках ТФН записываются значения функций при соответствующих наборах. Ниже приведена ТФН для трёхвходного элемента И-НЕ (табл. 1).
Таблица 1
| е |
| ||||||||||
| х1 | х2 | х3 | 
| 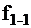
| 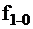
| 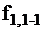
| 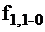
| 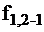
| 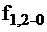
| 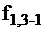
| 
|
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
где е – наборы сигналов на входе трёхвходного элемента И-НЕ;
 – правильное значение функции на выходе элемента И-НЕ;
– правильное значение функции на выходе элемента И-НЕ;
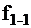 ‑ значение функции на выходе с фиксированным значением 1;
‑ значение функции на выходе с фиксированным значением 1;
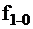 ‑ значение функции на выходе с фиксированным значением 0;
‑ значение функции на выходе с фиксированным значением 0;
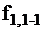 ‑ значение функции на выходе при сигнале на входе
‑ значение функции на выходе при сигнале на входе  ;
;
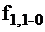 ‑ значение функции на выходе при сигнале на входе
‑ значение функции на выходе при сигнале на входе 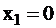 ;
;
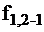 ‑ значение функции на выходе при сигнале на входе
‑ значение функции на выходе при сигнале на входе 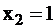 и т. д.
и т. д.
Аналогичные таблицы можно построить для любой логической схемы. Строки таблиц соответствуют входным наборам, столбцы — неисправностям схем, под которыми понимают неисправности элементов. Из табл. 1 видно, что для всех неисправностей можно найти входной набор, на котором 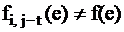 (функция неисправности не равна исправной), то есть все неисправности обнаруживаются. Некоторые неисправности отличаются друг от друга (
(функция неисправности не равна исправной), то есть все неисправности обнаруживаются. Некоторые неисправности отличаются друг от друга (  ,
, 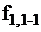 ,
, 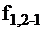 и
и 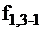 ), а значения функций
), а значения функций 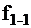 ,
, 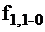 ,
, 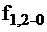 и
и  одинаковы на всех наборах и неразличимы между собой. С помощью полученной ТФН можно строить оптимальные алгоритмы диагностирования. Для этого ТФН целесообразно преобразовать: объединить неразличимые столбцы (
одинаковы на всех наборах и неразличимы между собой. С помощью полученной ТФН можно строить оптимальные алгоритмы диагностирования. Для этого ТФН целесообразно преобразовать: объединить неразличимые столбцы ( 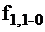 ,
, 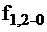 ,
,  ) и отметить клетки таблицы знаком (+), значения функции в которых отличаются от исправных значений (табл. 2).
) и отметить клетки таблицы знаком (+), значения функции в которых отличаются от исправных значений (табл. 2).
Для определения минимальной совокупности тестов (наборы сигналов) необходимо составить минимальное покрытие столбцов преобразованной ТФН. Из табл. 2 видно, что минимальная совокупность тестов, выявляющая все неисправности, содержит наборы 011, 101, 110, 111.
Анализ результатов проверки производится по ТФН. Например, если на указанных наборах выходной сигнал принимает значения соответственно (011) 0, то схема находится в состоянии  (неисправность при сигнале на входе
(неисправность при сигнале на входе  ), если (101) 0, – в состоянии
), если (101) 0, – в состоянии 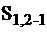 и при (110) 0 в состоянии
и при (110) 0 в состоянии 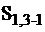 . Реакция на набор (111) равная 0 соответствует исправной схеме.
. Реакция на набор (111) равная 0 соответствует исправной схеме.
Таблица 2
| х1 | х2 | х3 | 
| 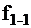
| 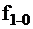
| 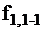
| 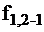
| 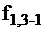
|
| 0 | 0 | 0 | 1 | + | ||||
| 0 | 0 | 1 | 1 | + | ||||
| 0 | 1 | 0 | 1 | + | ||||
| 0 | 1 | 1 | 1 | + | + | |||
| 1 | 0 | 0 | 1 | + | ||||
| 1 | 0 | 1 | 1 | + | + | |||
| 1 | 1 | 0 | 1 | + | + | |||
| 1 | 1 | 1 | 0 | + |
Таблицы функций неисправностей являются универсальным средством для построения алгоритмов проверки любых устройств. Однако ТФН обладают существенным недостатком: они громоздки, что значительно затрудняет выбор минимальной совокупности тестов и анализ полученных результатов. Упростить разработку тестов позволяют аналитические методы определения минимальных тестовых наборов, разработанные для комбинационных логических схем.
Активизация критического пути или D-алгоритм основан на анализе математической модели схемы и проведении логических экспериментов продвижения неисправности к выходам и входам схемы. При этом используется троичное моделирование, когда тот или иной аргумент на входе и выходе схемы может принимать как истинные значения 0 и 1, так и значение D. Полагают, что значения  и
и  в исправной, а
в исправной, а 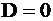 и
и 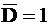 в неисправной схемах.
в неисправной схемах.
В табл. 3 приведены функции, реализуемые элементами И и ИЛИ при наличии одиночных неисправностей D и  .
.
Таблица 3
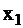
| 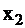
| (И) 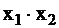
| (ИЛИ) 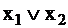
| 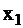
| 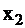
| (И) 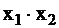
| (ИЛИ) 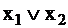
|
| 0 | 0 | 0 | 0 | 
| 0 | 0 | 
|
| 1 | 0 | 0 | 1 | 0 | 
| 0 | 
|
| 0 | 1 | 0 | 1 | 1 | 
| 
| 1 |
| 1 | 1 | 1 | 1 | 
| 1 | 
| 1 |

| 0 | 0 | 
| 1 | 
| 
| 1 |
| 0 | 
| 0 | 
| 
| 1 | 
| 1 |
Из табл. 3 видно, что ошибка на входе элементов (сигнал D) не всегда проявляется на его выходе, то есть не всегда является критической. Так, для элемента И ошибка на одном из входов является критической только в том случае, если все другие входные сигналы равны 1, а для элемента ИЛИ — если на все входы, кроме контролируемого, подан 0. Поэтому при тестировании необходимо создать такие условия, при которых возникший дефект обязательно проявится на выходе схемы.
· На реализации этого принципа и основана разработка D-алгоритма, состоящего из следующих этапов:
· выбирают узел схемы и присваивают ему значение  или
или  , мысленно продвигаются к входу и выходу схемы, выбирая значения входных сигналов элементов, обеспечивающих критическое значение на каждом последующем выходе до выхода схемы;
, мысленно продвигаются к входу и выходу схемы, выбирая значения входных сигналов элементов, обеспечивающих критическое значение на каждом последующем выходе до выхода схемы;
· повторяют описанную процедуру для каждого узла схемы.
Так как значение D противоположно значению сигнала в исправной схеме, то полученные наборы входных сигналов позволяют выявить все заданные неисправности.
Пример 1. Рассмотрим схему, изображённую на рис. 1.
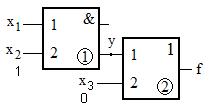 Рис. 1. Логическая схема
Рис. 1. Логическая схема
| Узлами схемы являются все входы и выходы элементов. Разработку D алгоритма начнём с входа 1 элемента  . Для активизации критического пути необходимо, чтобы . Для активизации критического пути необходимо, чтобы 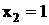 , а , а 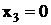 (выводы из табл. 3). Таким образом, неисправность (выводы из табл. 3). Таким образом, неисправность  (на выходе f=0) появится на наборе (х1, х2, х3) 110, a неисправность (на выходе f=0) появится на наборе (х1, х2, х3) 110, a неисправность  (на выходе f=1) — на наборе 010. (на выходе f=1) — на наборе 010.
|
Неисправность на выходе элемента 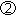 (на выходе f=1) при
(на выходе f=1) при 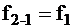 (на входе Х1=1) фиксируется при Х3=0: при этом сигналы Х1 и Х2 должны обеспечивать значения
(на входе Х1=1) фиксируется при Х3=0: при этом сигналы Х1 и Х2 должны обеспечивать значения  и
и 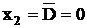 . Аналогично проводят анализ остальных узлов схемы (у, и
. Аналогично проводят анализ остальных узлов схемы (у, и 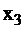 ), то есть построчно вносим изменения в наборы входных сигналов, включая значение у, для появления ошибки на выходе схемы f.
), то есть построчно вносим изменения в наборы входных сигналов, включая значение у, для появления ошибки на выходе схемы f.
Результаты разработки теста сведены в табл. 4.
Таблица 4
| х1х2х3 | 
| 
| 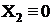
| 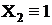
| 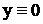
| 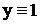
| 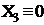
| 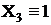
| 
| 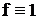
|
| 000 | + | + | испр. | + | ||||||
| 001 | + | + | испр. | |||||||
| 010 | + | + | + | испр. | + | |||||
| 011 | + | + | испр. | |||||||
| 100 | + | + | + | испр. | + | |||||
| 101 | + | + | испр. | |||||||
| 110 | + | + | + | + | испр. | |||||
| 111 | + | испр. |
Примечание. Знак «+» означает проявление неисправности на данном наборе;
«  » ‑ тождество или тождественно равно.
» ‑ тождество или тождественно равно.
По максимальному числу неисправностей из табл. 4 составим минимальное покрытие тестовых сигналов. Получим минимальный контролирующий тест ТК для схемы рис. 1: ТК = {001, 010, 100, 110}.
Диагностирование схемы производится подачей на её входы тестовых наборов и фиксацией выходного сигнала, значения которого для исправной и неисправной схем приведены в табл. 5. Появление сигнала неисправности fH даже на одном тестовом наборе свидетельствует о наличии дефекта.
| Таблица 5
| Метод обнаружения неисправностей в комбинационных логических схемах, — это подача на входы х1, х2,, …, хn полного набора 2n сигналов и сопоставление полученного сигнала выхода 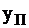 с расчётным с расчётным 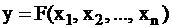 . .
|
Если хотя бы на одном наборе входов  , то схема неисправна.
, то схема неисправна.
Способ можно упростить, сократив количество необходимых тестовых воздействий, и сделать его более информативным, указав, какой конкретно вход неисправен в предположении, что неисправность одиночная.
Формирование минимизированного набора тестовых воздействий осуществляют методом булевой производной, то есть проверкой определённого входа хi логической схемы ЛС (рис. 2).
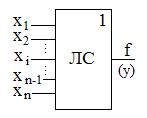 Рис. 2. Функциональная схема комбинационного логического устройства
Рис. 2. Функциональная схема комбинационного логического устройства
| Для этого на все остальные входы должна быть поданы такие сигналы, чтобы выход зависел от хi. Так для контроля одного из входов x1 схемы ИЛИ нужно на все остальные входы подать сигналы 0. Пусть на входе x1 возникла одна из двух возможных константных неисправностей 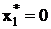 , которая обнаруживается, если подан npoтивоположный сигнал Х1=1. Соответственно для выявления не- , которая обнаруживается, если подан npoтивоположный сигнал Х1=1. Соответственно для выявления не-
|
исправности 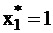 надо подать сигнал
надо подать сигнал 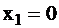 . Таким образом, полное число тестовых наборов не превышает 2n.
. Таким образом, полное число тестовых наборов не превышает 2n.
Булева производная от функции у по переменной хi определяется как:


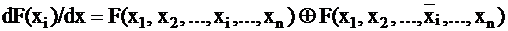 .
.
Принимаем  и
и  , и обозначим
, и обозначим  , а
, а 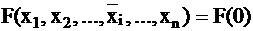 . Тогда производная запишется как:
. Тогда производная запишется как:
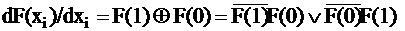 .
.
Если F(1) = F(0), то значения сигнала на 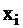 не влияет на у, и неисправность не будет обнаружена. Необходимым условием её обнаружения является
не влияет на у, и неисправность не будет обнаружена. Необходимым условием её обнаружения является  или
или 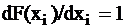 .
.
Например, для трёхвходового логического элемента И сигнал на выходе будет равен:  . Для проверки входа х1 определяем необходимые сигналы на входах х2 и х3:
. Для проверки входа х1 определяем необходимые сигналы на входах х2 и х3: 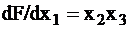 . Условием контролируемости входа х1 для обнаружения ошибки является:
. Условием контролируемости входа х1 для обнаружения ошибки является:  , то есть
, то есть 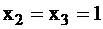 . Тогда тестовые сигналы для х1 будут равными {011, 111}. Аналогично для проверки входа х2 определяем необходимые сигналы на входах х1 и х3:
. Тогда тестовые сигналы для х1 будут равными {011, 111}. Аналогично для проверки входа х2 определяем необходимые сигналы на входах х1 и х3: 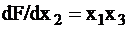 ,
, 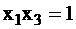 , то есть
, то есть 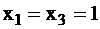 . Тогда тестовые сигналы для х2 образуют множество {101, 111}.
. Тогда тестовые сигналы для х2 образуют множество {101, 111}.
Пример 2. Для схемы рис. 1 находим значение входных сигналов, позволяющих обнаружить наличие неисправности в точке У. Для этого входную функцию для элемента 2 запишем в виде 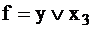 .
.
Определим 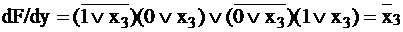 . Приравняв производную единице
. Приравняв производную единице 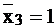 , находим, что для обнаружения отказа в точке У необходимо подать на вход
, находим, что для обнаружения отказа в точке У необходимо подать на вход 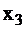 нулевой сигнал, то есть
нулевой сигнал, то есть 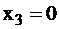 (неисправность типа 0).
(неисправность типа 0).
Таким образом, набор значений переменных, обнаруживающий константную неисправность типа 0 в точке 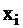 даёт решение уравнения предполагающее, что в соответствующую точку приходит сигнал
даёт решение уравнения предполагающее, что в соответствующую точку приходит сигнал  (в рассматриваемом примере в точку У):
(в рассматриваемом примере в точку У):
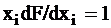 , (1)
, (1)
Возникающая неисправность на выходе схемы приводит к появлению в точке У сигнала равного 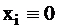 , что вызывает изменение выходной функции.
, что вызывает изменение выходной функции.
Аналогично, решение уравнения
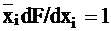 (2)
(2)
определяет набор значений входных переменных, обнаруживающий константную неисправность типа 1, то есть когда 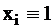 .
.
Пример 3. Для примера 2 определяем значения диагностирующих наборов входных переменных: 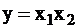 ,
,  ,
, 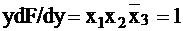 ;
;  . Отсюда получаем тестовые наборы, проверяющие неисправности типов 0: — 110 и типа 1: — 010 или 100.
. Отсюда получаем тестовые наборы, проверяющие неисправности типов 0: — 110 и типа 1: — 010 или 100.
Приведём ряд свойств булевой производной, облегчающих разработку тестов, контролирующих работу логической схемы:
1) Булева производная  не зависит от
не зависит от 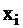 . Это упрощает разработку тестовых наборов для выявления отказа в выходном узле схемы. Тестовые воздействия определяют из решения уравнений
. Это упрощает разработку тестовых наборов для выявления отказа в выходном узле схемы. Тестовые воздействия определяют из решения уравнений 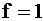 и
и 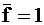 ;
;
2) Если  , то неисправность в точке
, то неисправность в точке 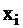 выявляется при любых значениях остальных переменных;
выявляется при любых значениях остальных переменных;
3) Если 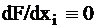 , то это означает, что не существует ни одного набора тестов, позволяющего обнаружить неисправность в данной точке.
, то это означает, что не существует ни одного набора тестов, позволяющего обнаружить неисправность в данной точке.
Для определения полного набора тестовых воздействий необходимо решить уравнения (1) и (2) для всех узлов схемы или для всех переменных описывающей её логической функции. Минимизация теста проводится путём составления минимального покрытия ТФН.
Пример 4. Определим наборы тестов для остальных узлов схемы, рис. 1.
1. Неисправность выхода: 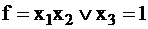 — на наборах 011 или 101;
— на наборах 011 или 101;
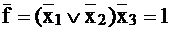 — на наборах 100 или 010.
— на наборах 100 или 010.
2. Неисправность входа 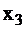 :
:
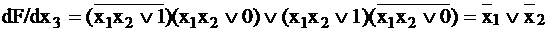 ,
,
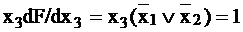 ‑ на наборе 101 или 110;
‑ на наборе 101 или 110;
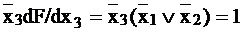 ‑ на наборах 001 или 010.
‑ на наборах 001 или 010.
3. Неисправность входа 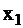 :
:
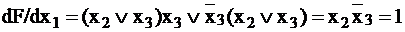 ,
,
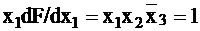 — на наборе 110;
— на наборе 110;
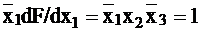 ‑ на наборе 010.
‑ на наборе 010.
4. Неисправность входа 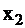 :
:
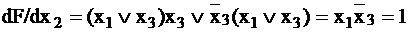 ,
,
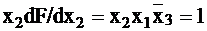 — на наборе 110;
— на наборе 110;
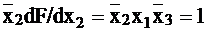 ‑ на наборе 010.
‑ на наборе 010.
Можно легко убедиться, что полученные результаты полностью совпадают с тестом, разработанным с использованием D-алгоритма (см. табл. 4 и 5).
Таблицу функций неисправностей ТФН используют для построения не только контролирующего теста, но и диагностирующего теста, обеспечивающего большую глубину поиска дефекта
Выбрать минимальную совокупность диагностирующих наборов входных переменных можно следующим образом:
1) преобразовать ТФН, объединив между собой одинаковые столбцы, то есть объединить неразличимые по изменению выходного сигнала неисправности;
2) в преобразованной ТФН отметить столбцы, содержащие лишь один знак «+», и выделить наборы входных переменных 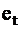 соответствующие этим знакам;
соответствующие этим знакам;
3) составить таблицу функций 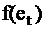 и
и 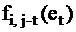 записав в неё логические значения функций на соответствующих наборах;
записав в неё логические значения функций на соответствующих наборах;
4) если в полученной таблице имеются одинаковые столбцы, то по исходной ТФН определить наборы входных переменных, на которых эти столбцы различаются, и дополнить таблицу минимально необходимым числом таких наборов.
Пример 5. Для примера 3 неразличимы неисправности (см табл. 4) 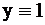 ,
, 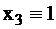 , и
, и 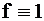 ,
, 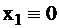 ,
,  ,
, 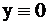 ,
, 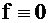 . Сокращённая ТФН показана в табл. 6. В табл. 6 единственным знаком «+» отмечены столбцы 1, 2 и 3, им соответствуют наборы 010, 100 и 110. Значения исправной и неисправной функции на этих наборах сведены в табл. 7, где в столбце 0 приведены значения функции
. Сокращённая ТФН показана в табл. 6. В табл. 6 единственным знаком «+» отмечены столбцы 1, 2 и 3, им соответствуют наборы 010, 100 и 110. Значения исправной и неисправной функции на этих наборах сведены в табл. 7, где в столбце 0 приведены значения функции 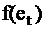 , а номера функций
, а номера функций  соответствуют табл. 6.
соответствуют табл. 6.
Таблица 6
|
| 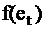
| 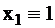
| 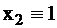
| 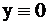
| 
| 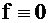
| 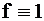
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 000 | 0 | + | |||||
| 001 | 1 | + | + | ||||
| 010 | 0 | + | + | ||||
| 011 | 1 | + | + | ||||
| 100 | 0 | + | + | ||||
| 101 | 1 | + | + | ||||
| 110 | 1 | + | + | ||||
| 111 | 1 | + |
Таблица 7
|
| 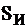
| 
| 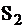
| 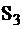
| 
| 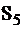
| 
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
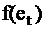
| 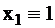
| 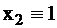
| 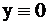
| 
| 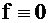
| 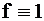
| |
| 010 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 100 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 110 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| . . . . . . . 001 | . . . . . . 1 | . . . . . . 1 | . . . . . . 1 | . . . . . . 1 | . . . . . . 0 | . . . . . . 0 | . . . . . . 1 |
Из табл. 7 видно, что неразличимы столбцы 0 и 4, 3 и 5. Первая пара функции (0 и 4) отличается друг от друга на наборах 001, 011, 101 и 111, и вторая — на тех же наборах 001, 011, 101 и 101. Дополнив табл. 7 любым из последней тройки наборов, например набором 001, получим ТФН, обеспечивающую максимальную глубину диагноза. В рассматриваемом примере контролирующий и диагностический тесты одинаковые, но процесс диагностирования в обоих случаях различен.
Граф алгоритма проверки исправности схемы рис. 1 показан на рис. 3а), на рис. 3б) приведен граф алгоритмического диагностирования.
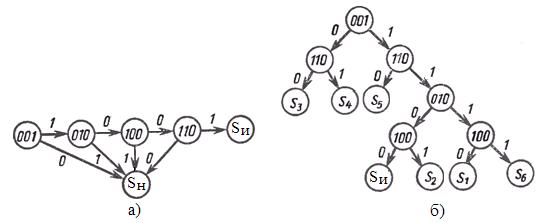
Рис. 3. Графы алгоритмов проверки логической схемы:
а) — при проверке неисправности; б) — при диагностировании
В промежуточных вершинах графов указаны проверочные наборы, а в конечных — выявленные состояния (индексы на рис. 3а) соответствуют номерам столбцов табл. 6). Из рис. 3а), б) видно, что при проверке исправности последовательность подачи тестов безразлична, а при диагностировании очередной тест выбирается с учётом полученного ранее результата.
Примечание. По табл. 7 строим граф для диагностирования схемы. Его построение можно проводить с любого набора согласно ТФН, поэтому диагностические графы могут отличаться. Вершины графа соответствуют состояниям автомата, в которых отражены наборы минтермов 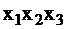 , дуги – переходам автомата в состояния 0 или1, поэтому в различных вершинах могут быть одинаковые наборы. Возьмём вершину с набором 001: он может перейти в набор 110, который может находиться в состоянии 0 или 1. В состоянии 0 в нём будет
, дуги – переходам автомата в состояния 0 или1, поэтому в различных вершинах могут быть одинаковые наборы. Возьмём вершину с набором 001: он может перейти в набор 110, который может находиться в состоянии 0 или 1. В состоянии 0 в нём будет  также находится в нём либо при 0 либо при 1. При 0, в нём
также находится в нём либо при 0 либо при 1. При 0, в нём  , а
, а 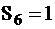 . При 1,
. При 1, 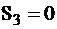 . Далее переходим к вершине 010 переходящей к вершине 100 которая может принимать значения 0 или1. При 0, если
. Далее переходим к вершине 010 переходящей к вершине 100 которая может принимать значения 0 или1. При 0, если 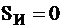 , а
, а 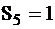 . При 1 имеем
. При 1 имеем 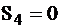 , а
, а 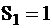 .
.
Диагностирование автомата с памятью значительно труднее по сравнению с диагностированием комбинационных схем. Это объясняется тем, что состояние выхода автомата с памятью зависит не только от текущего состояния входа, но и от предшествующего состояния автомата Методы синтеза проверяющих тестов для автоматов с памятью также основаны на анализе и сравнении моделей исправного и неисправного автоматов. В результате анализа выбираются входные и выходные последовательности сигналов, позволяющие обнаружить заданное множество неисправностей. В качестве моделей автомата, как правило, используют таблицы состояний и выходов, что и предопределяет трудоёмкость процедур теста и ограничение области их применения сравнительно простыми устройствами. В ответственных устройствах, содержащих резервные узлы, аппаратурную и информационную избыточность для контроля можно использовать состояние узлов в процессе работы (функциональное диагностирование).
Однако усложнение цифровых устройств, повышение разрядности данных и быстродействия, широкое распространение программных методов управления привели к серьёзным затруднениям при их отладке и диагностировании. Контроль сложных цифровых и особенно микропроцессорных систем требует регистрации последовательности логических состояний одновременно во многих узлах схемы на протяжении значительного временного интервала.
Для решения задач отладки и проверки сложных цифровых систем используются специальные приборы, называемые логическими анализаторами, которые предназначены для измерений потоков двоичных данных. В процессе работы логический анализатор подключается к выбранным точкам контролируемой схемы и принимает в запоминающее устройство последовательности логических состояний контрольных точек. Тактовые сигналы записи в запоминающее устройство вырабатываются внутренним генератором или поступают от контролируемой схемы. В современных логических анализаторах число каналов достигает 48, длина последовательности 2048 бит/кан, а максимальная частота записи — 50 МГц. Режим записи продолжается до появления заданного оператором события: внешнего сигнала, состояния выхода, числа тактов записи. В режиме индикации собранная информация выводится в формате, выбранном оператором. Так как анализатор обладает памятью, режим индикации не зависит от условий записи. Индикация продолжается сколь угодно долго, при этом оператор меняет режимы индикации, выводит данные с разной степенью подробности, сравнивает результаты измерений с эталонными и т. д.
Логический анализатор — универсальное диагностирующее устройство, применяемое для любых цифровых систем. Однако его использование требует высокой квалификации оператора и знания им принципов работы проверяемой системы. Кроме того, для каждой конкретной неисправности необходимо заново разрабатывать процедуру испытаний, настраивать прибор и систему на требуемый режим работы, выбирать контрольные точки. Логический анализатор — сложный и дорогостоящий прибор, поэтому он малопригоден для эксплуатационного обслуживания. Это и явилось причиной поиска нового способа испытаний цифровых систем, который, не требуя высокой квалификации персонала, позволил бы быстро и точно отыскать неисправный элемент с помощью недорогого и компактного оборудования. Таким способом стал сигнатурный анализ.
Сигнатурный анализ основан на преобразовании длинных последовательностей входных сигналов в двоичное число, называемое сигнатурой. Измеряемые двоичные последовательности возбуждаются в контрольных узлах под действием тестовой последовательности двоичных входных слов и тактовых сигналов. Сигнатуры контрольных узлов измеряются на исправной системе и указываются на принципиальной схеме так, как на схемах аналоговых устройств показаны параметры сигналов или их осциллограммы. Для удобства сигнатура дана в виде нескольких (обычно, четырёх) шестнадцатеричных цифр. При поиске неисправностей оператор устанавливает режим исполнения тестовой программы и, прослеживая сигнатуры в контрольных узлах схемы от выходов к входам, ищет элемент, у которого входные сигнатуры верны, а выходные нет.
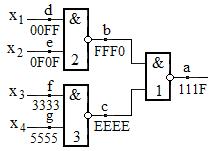 Рис. 4. Обозначение сигнатур на принципиальной схеме
Рис. 4. Обозначение сигнатур на принципиальной схеме
| Пример 6. На рис. 4 приведена логическая схема, на которой обозначены контрольные точки а — g и их сигнатуры 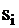 при подаче на входы при подаче на входы 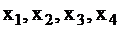 — последовательности двоичных сигналов 0000, 0001, …, 1110, 1111, например, с выходов четырёхразрядного двоичного счётчика. Сигнатуры могут быть измерены с помощью сдвигового регистра, синхронизируемого тактовым генератором счётчика. На рис. 5 показана схема алгоритма поиска неисправности. — последовательности двоичных сигналов 0000, 0001, …, 1110, 1111, например, с выходов четырёхразрядного двоичного счётчика. Сигнатуры могут быть измерены с помощью сдвигового регистра, синхронизируемого тактовым генератором счётчика. На рис. 5 показана схема алгоритма поиска неисправности.
|
Алгоритм поиска, основанный на получении и сравнении сигнатур, относится к классу алгоритмов с восстановлением и позволяет выявлять одиночные и кратные неисправности. Как видно из рис. 5, этот алгоритм позволяет осуществлять и частичный самоконтроль диагностирующего устройства, выявляя неисправность генератора тестов.

Рис. 5. Алгоритм диагностирования путём сигнатурного анализа
Если совершается логическое условие (а=1)  , то схема исправна. При а = 0 на выходах схем 2 и 3 должны быть 1, (b = c = 1), если а ≠ 0, то неисправна ИМС 1. Если b = c = 0, то переходим к состояниям на их входах: в точках d = e = 1, а в точке b ≠ 0, то неисправна ИМС 2 и т. д.
, то схема исправна. При а = 0 на выходах схем 2 и 3 должны быть 1, (b = c = 1), если а ≠ 0, то неисправна ИМС 1. Если b = c = 0, то переходим к состояниям на их входах: в точках d = e = 1, а в точке b ≠ 0, то неисправна ИМС 2 и т. д.
Существует много способов сжатия двоичных последовательностей в сигнатуры. Сравнительный анализ показал, что наиболее эффективен способ, основанный на преобразовании с помощью шестнадцатиразрядного сдвигового регистра с линейными обратными связями. Функциональная схема такого регистра показана на рис. 6.
Выявление ошибки во входной последовательности основано на том, что за счёт линейной обратной связи она начинает циркулировать в сдвиговом регистре, изменяя текущую сигнатуру. Если длина входной последовательности n меньше длины регистра m, то ошибка, попавшая в регистр, не успеет выйти из него до окончания формирования сигнатуры и обязательно обнаружится. При увеличении длины входной последовательности (n > m) некоторые ошибки не обнаруживаются, так как дают нулевое приращение сигнатуры, однако вероятность обнаружения, выражаемая формулой 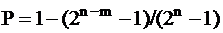 , близка к единице. При длине регистра m = 16 независимо от длины последовательности n ошибка произвольной кратности обнаруживается с вероятностью не ниже 0,99998, что отвечает нормативным требованиям к достоверности диагностической информации.
, близка к единице. При длине регистра m = 16 независимо от длины последовательности n ошибка произвольной кратности обнаруживается с вероятностью не ниже 0,99998, что отвечает нормативным требованиям к достоверности диагностической информации.
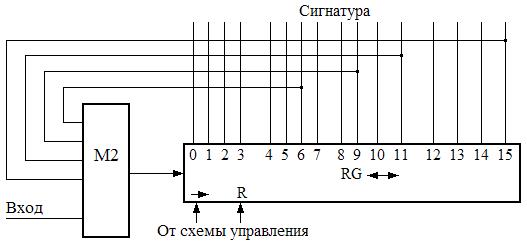
Рис. 6. Функциональная схема сигнатурного регистра
Диагностирующее устройство кроме сигнатурного анализатора должно содержать генератор тестовых воздействий, последовательность которых вызывает проявление заданного класса дефектов в контролируемых узлах схемы. Таким генератором может служить последовательный двоичный счётчик, разрядность которого определяется числом входов диагностируемого устройства. Однако следует иметь в виду, что достоверность результата уменьшается с увеличением длины тестовой последовательности. Важным узлом диагностирующего устройства является и формирователь измерительного окна, то есть схема, определяющая интервал времени, в течение которого формируются тестовые сигналы и накапливается сигнатура. Формирователь обеспечивает синхронизацию работы анализатора и контролируемого устройства.
Одно из основных требований к диагностируемым устройствам — возможность обеспечения разрыва обратных связей между элементами схемы. Сигнатурный анализ не позволяет локализовать неисправность внутри контура обратной связи, так как при этом нет ни одного элемента в цепи, у которого при неправильной сигнатуре выхода были бы правильными входные сигнатуры. Так как микропроцессорные системы полностью охвачены обратной связью по контуру программного управления, для применения сигнатурного анализа необходимо разрывать этот контур, например, отключением магистрали данных от входа МП. На время проверки входы данных МП подключаются к специальному ПЗУ, в котором хранится тестовая программа, в качестве которой можно применять и рабочую программу, если она использует все устройства системы.
В настоящее время разработаны сигнатурные анализаторы, которые сами генерируют тестовое воздействие на диагностируемую систему. При испытаниях МПС генератор тестовых сигналов подключают к системе через сокет (разъём) микропроцессора. При этом проблема разрыва обратной связи решается сама собой. Такой подход к сигнатурному анализу открывает широкие возможности для автоматизации проведения испытаний.
ТЕМЫ КУРСОВЫХ РАБОТ по АРЭС для гр. ЭЭБЗ-06-14
выдано 00.10.2017г

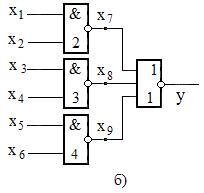


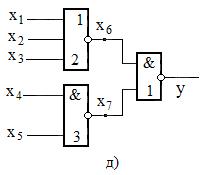

Определить набор тестовых сигналов для диагностирования логической схемы при неисправном узле 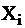 согласно таблицы задания.
согласно таблицы задания.
Таблица
| № п/п | Ф. И. О. | Рисунок | Узел | № п/п | Ф. И. О. | Рисунок | Узел |
| 1. | а) | х6 | 6. | б) | х9 | ||
| 2. | в) | х6 | 7. | в) | х5 | ||
| 3. | б) | х8 | 8. | г) | х6 | ||
| 4. | г) | х7 | 9. | д) | х6 | ||
| 5. | д) | х7 | 10. | е) | х6 |
Диагностирование заданной логической схемы провести с помощью различных математических моделей объекта:
а) таблицей функций неисправностей ТФН;
б) методом активизации критического пути (D-алгоритма);
в) методом булевой производной;
По полученным результатам изобразить граф алгоритмической проверки заданной заданием логической схемы.
Литература:
1. Электронные промышленные устройства: Учеб. для студ. вузов спец. «Пром. электрон.»/ В.И. Васильев, Ю.М. Гусев, В.Н. Миронов и др. – М.: Высш. шк., 1988. – 303 с.: ил.
Дата добавления: 2018-02-15; просмотров: 723; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ,
,