Повторение испытаний. Функция и плотность распределение случайной величины
Министерство образования Российской Федерации
Пермский государственный технический университет
Кафедра прикладной математики
Теории вероятностей
(сборник индивидуальных заданий)
Пермь, 2009
Составители Р.Ф. Валеева
Р.Х. Спицина
Настоящий сборник предназначен для студентов инженерно-технических специальностей, изучающих раздел математики «Теория вероятностей».
Сборник содержит расчетную работу, состоящую из двух заданий (№1 и №2) и 30 вариантов контрольной домашней работы (задания №3 - №7).
Приводится подробное решение одного варианта расчетной работы.
Материалы сборника могут быть использованы студентами для самостоятельной работы в течении семестра, а также преподавателями на практических занятиях и при подготовке контрольных заданий.
Раздел 1 Теория вероятностей
Расчетная графическая работа 1
1.1 Основые понятия и теоремы теории вероятностей
Задание № 1
1. Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта (V – номер варианта).
2. Определить испытания и элементарные события.
3. Определить исследуемое событие А и другие события.
4. Установить, какие формулы следует использовать для вычислений и выполнить последние. Вычисления произвести, по возможности точно.
Задача 1.1.
Бросают две монеты. Найти вероятность того, что:
|
|
|
1) на обеих монетах появится «герб»,
2) хотя бы на одной монете появится «герб»,
3) ни на одной монете не появится «герб»,
Бросают три монеты. Найти вероятность того, что:
4) на всех монетах появится «герб»,
5) хотя бы на одной монете появится «герб»,
6) только на двух монетах появится «герб»,
7) только на одной монете появится «герб»,
8) ни на одной монете не появится «герб»,
Бросают четыре монеты. Найти вероятность того, что:
9) на всех монетах появится «герб»,
10) хотя бы на одной монете появится «герб»,
11) только на одной монете появится «герб»,
12) только на двух монетах появится «герб»,
13) только на трех монетах появится «герб»,
14) ни на одной монете не появится «герб»,
Бросают игральную кость. Найти вероятность того, что на верхней грани появится:
15) четное число очков;
16) «1» или «6».
Бросают две игральные кости. Найти вероятность того, что на верхней грани появятся следующие числа очков:
17) только четные;
18) одно четное, другое нечетное;
19) сумма которых четна;
20) сумма которых нечетна;
21) сумма которых больше, чем их произведение;
22) сумма которых меньше шести;
23) сумма которых больше восьми.
Бросают три игральные кости. Найти вероятность того, что на верхних гранях появятся следующие числа очков:
|
|
|
24) только четные;
25) одно четное, остальные нечетные;
26) сумма которых четна;
27) сумма которых нечетна;
28) которые все одинаковы;
29) которые все различны;
30) сумма которых делится на четыре;
Задача 1.2.
Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность того, что буквы вынимаются в порядке заданного слова.
Слова по вариантам:
0) МАТЕМАТИК 16) ПАМЯТЬ
1) ПРОГРАММА 17) УСТРОЙСТВО
2) ПРОГРАММИСТ 18) ПЕРФОЛЕНТА
3) ПРОГРАММИРОВАНИЕ 19) ПЕРФОКАРТА
4) СТАТИСТИК 20) ФЕРРИТ
5) СТАТИСТИКА 21) МАГНИТ
6) СОБЫТИЕ 22) ГИСТЕРЕЗИС
7) СЛУЧАЙНОСТЬ 23) СЕРДЕЧНИК
8) ВЕРОЯТНОСТЬ 24) ПОЛУПРОВОДНИК
9) АЛГОРИТМ 25) ТРАНЗИСТОР
10) БЛОК-СХЕМА 26) ИНТЕГРАЛ
11) ПОДПРОГРАММА 27) КАЛЬКУЛЯТОР
12) ПРОЦЕДУРА 28) ВЫЧИСЛИТЕЛЬ
|
|
|
13) ПРИСВАИВАНИЕ 29) ОПЕРАЦИЯ
14) УСЛОВИЕ 30) АРИФМЕТИКА
15) ПРОЦЕССОР
Задача 1.3.
Как и в предыдущей задаче, найти соответствующую вероятность случая, когда заданным словом является ваша фамилия и ваше имя.
Задача 1.4.
В урне содержится К черных и Н белых шаров. Случайным образом вынимают М шаров. Найти вероятность того, что в них имеется:
а) Р белых шаров;
б) меньше, чем Р, белых шаров;
в) хотя бы один белый шар.
Значения параметров К, Н, М, и Р по вариантам приведены в табл.1.
Таблица1
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| К | 5 | 5 | 6 | 6 | 7 | 4 | 8 | 6 | 4 | 5 | 7 | 8 | 6 | 4 | 8 | 5 |
| Н | 6 | 6 | 5 | 5 | 4 | 5 | 6 | 7 | 7 | 6 | 4 | 6 | 5 | 6 | 6 | 6 |
| М | 4 | 5 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 4 | 4 | 5 | 5 |
| Р | 2 | 3 | 2 | 3 | 2 | 2 | 3 | 4 | 2 | 3 | 2 | 3 | 3 | 3 | 2 | 4 |
| Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| К | 7 | 5 | 6 | 5 | 6 | 6 | 6 | 8 | 6 | 5 | 6 | 5 | 6 | 6 | 4 |
| Н | 4 | 7 | 5 | 7 | 7 | 8 | 5 | 6 | 7 | 7 | 7 | 7 | 8 | 7 | 7 |
| М | 5 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 6 | 5 | 5 | 5 | 4 |
| Р | 3 | 3 | 2 | 4 | 3 | 4 | 4 | 3 | 3 | 2 | 3 | 3 | 3 | 2 | 2 |
|
|
|
Задача 1.5.
Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями 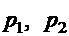 и
и 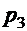 . Найти вероятность того, что за время Т выйдет из строя:
. Найти вероятность того, что за время Т выйдет из строя:
а) только один элемент;
б) хотя бы один элемент.
Значения параметров вычислить по следующим формулам:
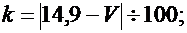
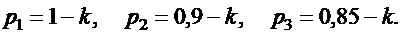
Задача 1.6.
В первой урне К белых и L черных шаров, а во второй - М белых и N черных. Из первой урны вынимают случайным образом Р шаров, а из второй – Q шаров. Найти вероятность того, что среди вынутых шаров:
1) все шары одного цвета;
2) только три белых шара;
3) хотя бы один белый шар.
Значения параметров K, L, M, N, P и Q по вариантам приведены в табл. 2.
Таблица 2
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| К | 6 | 5 | 4 | 7 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 3 | 3 | 3 | 3 |
| L | 4 | 5 | 5 | 3 | 4 | 6 | 7 | 8 | 3 | 5 | 6 | 7 | 8 | 7 | 6 | 5 |
| М | 5 | 4 | 5 | 6 | 7 | 7 | 6 | 7 | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 |
| N | 7 | 8 | 8 | 3 | 4 | 3 | 4 | 5 | 6 | 3 | 5 | 4 | 7 | 4 | 5 | 6 |
| Р | 3 | 2 | 2 | 3 | 1 | 3 | 2 | 4 | 3 | 2 | 4 | 2 | 2 | 3 | 1 | 4 |
| Q | 2 | 2 | 3 | 1 | 4 | 2 | 2 | 1 | 3 | 2 | 1 | 3 | 3 | 3 | 4 | 1 |
| Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| К | 3 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 7 | 7 | 7 | 7 | 7 | 7 |
| L | 4 | 3 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 4 | 5 | 6 | 7 | 8 |
| М | 6 | 4 | 7 | 7 | 8 | 7 | 7 | 7 | 7 | 4 | 8 | 4 | 4 | 4 | 8 |
| N | 7 | 9 | 3 | 4 | 3 | 5 | 6 | 7 | 8 | 8 | 5 | 6 | 7 | 4 | 5 |
| Р | 2 | 2 | 3 | 2 | 4 | 2 | 3 | 3 | 1 | 4 | 3 | 2 | 3 | 1 | 3 |
| Q | 2 | 3 | 3 | 3 | 1 | 2 | 2 | 3 | 4 | 1 | 3 | 2 | 2 | 4 | 3 |
Задача 1.7.
В урне содержится К черных и белых шаров, к ним добавляют L белых шаров. После этого из урны вынимают М шаров. Найти вероятность того, что все вынутые шары белые, полагая, что все возможные предположения о первоначальном содержании урны равновозможны.
Значения параметров К, L и М по вариантам приведены в табл. 3.
Таблица3
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| К | 4 | 3 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 |
| L | 2 | 4 | 3 | 2 | 4 | 4 | 4 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 |
| М | 3 | 4 | 4 | 3 | 4 | 2 | 3 | 2 | 3 | 4 | 2 | 3 | 4 | 5 | 2 | 3 |
| Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| К | 3 | 3 | 3 | 3 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| L | 4 | 5 | 5 | 5 | 5 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 |
| М | 5 | 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 | 2 | 3 | 4 | 5 | 2 | 3 |
Задача 1.8.
В одной урне К белых и L черных шаров, а в другой - M белых и N черных. Из первой урны случайным образом вынимают Р шаров и опускают во вторую урну. После этого из второй урны также случайно вынимают R шаров. Найти вероятность того, что все шары, вынутые из второй урны, белые.
Значения параметров K, L, M, N, P, R по вариантам приведены в табл. 4.
Таблица 4
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| К | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 6 | 6 | 6 | 6 | 6 |
| L | 6 | 5 | 4 | 3 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 8 | 7 | 6 | 5 | 4 |
| М | 4 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 3 | 3 | 3 | 3 |
| N | 8 | 7 | 6 | 5 | 4 | 3 | 5 | 4 | 6 | 7 | 8 | 9 | 3 | 4 | 5 | 6 |
| Р | 3 | 2 | 3 | 2 | 3 | 3 | 4 | 2 | 3 | 2 | 3 | 3 | 4 | 3 | 4 | 4 |
| R | 4 | 3 | 3 | 4 | 4 | 2 | 3 | 4 | 3 | 4 | 3 | 4 | 3 | 2 | 3 | 2 |
| Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| К | 6 | 6 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 7 | 7 | 7 | 7 | 7 |
| L | 3 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 2 | 3 | 4 | 5 | 6 | 7 |
| М | 3 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 2 | 2 | 2 | 2 | 2 | 2 |
| N | 7 | 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 8 | 6 | 5 | 4 | 3 | 2 |
| Р | 3 | 3 | 2 | 2 | 3 | 3 | 2 | 3 | 3 | 2 | 2 | 3 | 3 | 2 | 2 |
| R | 3 | 4 | 4 | 3 | 3 | 4 | 5 | 2 | 3 | 3 | 2 | 2 | 4 | 2 | 3 |
Задача 1.9.
В пирамиде стоят R винтовок, из них L с оптическим прицелом. Стрелок, стреляя, из винтовки с оптическим прицелом, может поразить мишень с вероятностью 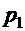 , а стреляя из простой винтовки – с вероятностью
, а стреляя из простой винтовки – с вероятностью 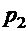 . Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Значения параметров вычислить по формулам:
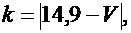
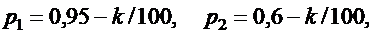
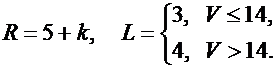
Задача 1.10.
В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве М1, М2, М3 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 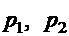 и
и 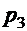 . Рабочий берёт случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом – изготовителем.
. Рабочий берёт случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом – изготовителем.
Значения параметров вычислить по следующим формулам:
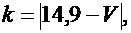
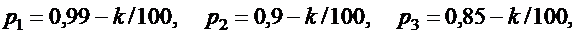
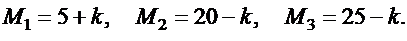
Повторение испытаний. Функция и плотность распределение случайной величины
Задание № 2
1. Переписать текст задачи, заменяя все параметры их значениями для вашего варианта.
2. Определить исходные данные и результаты.
3. Определить подходящие формулы вычисления и выполнить вычисления при помощи калькулятора и таблиц.
4. Построить требуемые графики.
Задача 2.1.
В каждом из n независимых испытаний событие А происходит с постоянной вероятностью р. Вычислить все вероятности 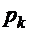 , k=0,1,2 …n, где k – частота события А. Построить график вероятностей
, k=0,1,2 …n, где k – частота события А. Построить график вероятностей 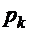 , найти наивероятнейшую частоту.
, найти наивероятнейшую частоту.
Значения параметров n и р вычислить по следующим формулам:
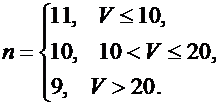 где V – номер варианта; р = 0,3 + 0,02 V.
где V – номер варианта; р = 0,3 + 0,02 V.
Задача 2.2.
В каждом из n независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что событие А происходит:
а) точно М раз;
б) меньше, чем М и больше, чем L раз;
в) больше, чем М раз.
Значения параметров n, p, M и L вычислить по следующим формулам:
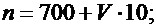
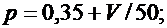
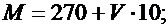
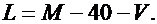
Задача 2.3.
В каждом из n независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что событие А происходит:
а) точно G раз;
б) точно L раз;
в) меньше чем М и больше чем F раз;
г) меньше чем R раз;
Значения параметров n, p, G, L, M, F и R вычислить по следующим формулам:
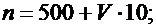
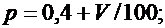
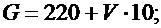
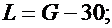
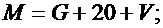
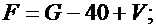
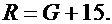
Задача 2.4.
На телефонной станции неправильное соединения происходит с вероятностью р. Найти вероятность того, что среди n соединений имеет место:
а) точно G неправильных соединений;
б) меньше, чем L неправильных соединений;
в) больше, чем М неправильных соединений.
Значение параметров р, n, G, L и M вычислить по следующим формулам:

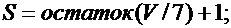
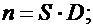
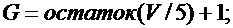
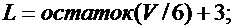
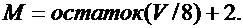
Задача 2.5.
В каждом из n независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что относительная частота k/n этого события отличается по абсолютной величине от вероятности р не больше, чем на ε > 0.
Значения параметров n, p, ε вычислить по следующим формулам
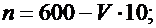
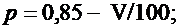
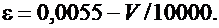
Задача 2.6.
Случайная величина Х задана рядом распределения
| Х | х1 х2 х3 х4 |
| P | р1 р2 р3 р4 |
Найти функцию распределения F(х) случайной величины Х и построить её график. Вычислить математическое ожидание M(X) и дисперсию D(X).
Значения параметров х1 , х2 , х3 , х4 , р1 , р2 , р3 , р4 вычислить по следующим формулам:
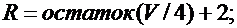
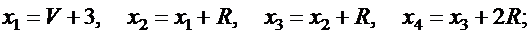
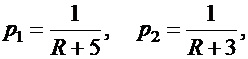
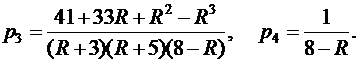
Задача 2.7.
Случайная величина Х задана функцией плотности вероятности
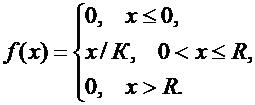
Найти функцию распределения F(x) случайной величины X. Построить графики функций f(х) и F(x). Вычислить математическое ожидание М(X) и дисперсию D(X).
Значения параметров К и R вычислить по следующим формулам:
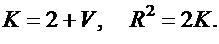
Задача 2.8.
Случайная величина Х задана функцией распределения
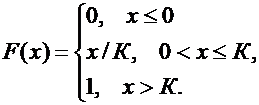
Найти функцию плотности вероятности f(х) случайной величины Х и построить графики функций f(х) и F(х). Вычислить для Х её математическое ожидание М(X) и дисперсию D(X).
Значения параметра К вычислить по формуле:
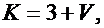 где V – номер варианта.
где V – номер варианта.
Задача 2.9.
Случайная величина Х распределена нормально. Найти вероятность того, что эта случайная величина принимает значение:
а) в интервале [а, b];
б) меньшее К;
в) большее L;
г) отличающееся от своего среднего значения по абсолютной величине не больше чем на ε.
Значения параметров m, σ , a, b, K, L и ε вычислить по формулам:
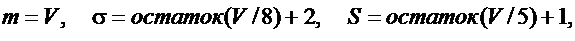
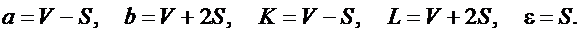
Задача 2.10.
Задана случайная величина Х 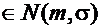 и точки х1 , х2 , х3 , х4 , х5, на числовой оси разделяющие ее на шесть интервалов. Найти вероятность того, что случайная величина Х принимает значения в этих интервалах.
и точки х1 , х2 , х3 , х4 , х5, на числовой оси разделяющие ее на шесть интервалов. Найти вероятность того, что случайная величина Х принимает значения в этих интервалах.
Значения m, σ , х1 , х2 , х3 , х4 , х5 вычислить по следующим формулам :
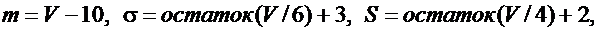
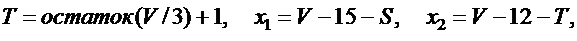
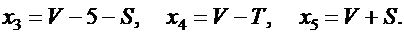
1.3Решение задач варианта расчетной работы
Задача 1.1.
Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять.
Определим испытание и его результат, т. е. элементарное событие. Испытанием является бросание трех игральных костей; результатом - одно из сочетаний очков 1,…,6 на верхних гранях трех костей.
Исследуемое событие А - сумма очков на трех костях делится на пять. Вероятность события А вычислим с помощью формулы:
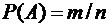
Общее количество элементарных событий п можно найти по правилу умножения. На каждой игральной кости 6 граней и все они могут сочетаться со всеми гранями других костей. Итак, получаем 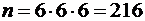 .
.
Количество элементарных событий m, входящих в состав события A или благоприятствующих событию A, найдем выписав всевозможные результаты испытаний и оставив из них только те, для которых сумма очков на всех трех костях делится на пять. Можно облегчить работу, выписав всевозможные исходы бросания первых двух костей, сочетая с ними подходящие значения количества очков, выпавших на третьей кости.
Имеем:
113 212 311 366 465 564 663
122 221 316 415 514 613
131 226 325 424 523 622
136 235 334 433 532 631
145 244 343 442 541 636
154 253 352 451 546 645
163 262 361 456 555 654
В результате получаем, что P(m) = 43, значит, P(A) = 43/216.
Ответ: P(A) = 43/216.
Задача 1.2.
Слово МАТЕМАТИКА составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность случая, когда буквы вынимаются в порядке заданного слова.
Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие А состоит в получении нужного слова МАТЕМАТИКА. Элементарные события являются перестановками из 10 букв, значит имеем n = 10!
Некоторые буквы в слове МАТЕМАТИКА повторяются (М - 2 раза, А - 3 раза, Т – 2 раза), поэтому возможны перестановки, при которых слово не изменяется. Их число равно
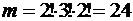
Таким образом,
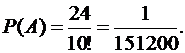
Ответ: Р(А)= 1/151200.
Задача 1.4.
В урне 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется:

а) 2 белых шара;
б) меньше чем 2 белых шара;
в) хотя бы один белый шар.
Испытанием будет случайное вынимание четырех шаров. Элементарными событиями являются всевозможные сочетания по 4 из 11 шаров. Их число равно
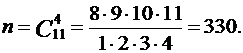
а) A1 - среди вынутых шаров 2 белых. Значит, среди вынутых шаров 2 белых и 2 черных. Используя правило умножения, получаем
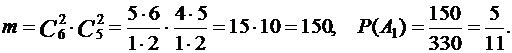
б) A2 — среди вынутых шаров меньше чем 2 белых. Это событие состоит из двух несовместных событий:
B1 - среди вынутых шаров только один белый и 3 черных шара,
B2 - среди вынутых шаров нет ни одного белого, все 4 шара черные:

Так как события B1 и B2 несовместны, можно использовать формулу
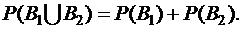
Имеем:
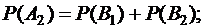
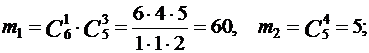
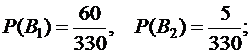
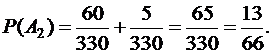
в) A3 - среди вынутых шаров хотя бы один белый. Этому событию удовлетворяют следующие сочетания шаров: 1 белый и 3 черных (B1), 2 белых и 2 черных (B2), 3 белых и 1 черный (B3), 4 белых (B4). Имеем
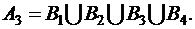
Здесь событие A3 определяется словами «хотя бы один» и прямое решение приводит обычно к сложным вычислениям. Проще сначала найти вероятность противоположного события и затем по формуле 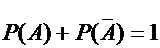 вычислить вероятность искомого события.
вычислить вероятность искомого события.
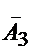 - среди вынутых шаров нет ни одного белого. В этом случае
- среди вынутых шаров нет ни одного белого. В этом случае
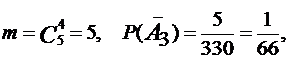
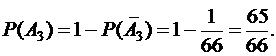
Ответ: P(A1) = 5/11, P(A2) = 13/66, P(A3) = 65/66.
Задача 1.5.
Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями 0,851, 0,751 и 0,701. Найти вероятность того, что за время Т выйдет из строя:
а) только один элемент;
б) хотя бы один элемент.
Испытание, т. е. работу за время T, нужно рассмотреть на двух уровнях: на уровне устройства и на уровне элементов. Элементарные события определять не надо, так как их вероятности заданы.
а) A1 - за время T выходит из строя только один элемент;
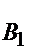 - первый элемент выходит из строя;
- первый элемент выходит из строя;
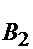 - второй элемент выходит из строя;
- второй элемент выходит из строя;
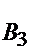 - третий элемент выходит из строя;
- третий элемент выходит из строя;
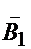 - первый элемент не выходит из строя;
- первый элемент не выходит из строя;
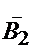 - второй элемент не выходит из строя;
- второй элемент не выходит из строя;
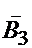 - третий элемент не выходит из строя.
- третий элемент не выходит из строя.
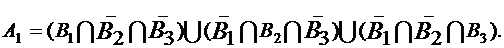
Учитывая независимость элементов устройств, несовместность событий Bi и 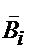 , и формулы
, и формулы 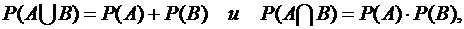 получаем следующую формулу:
получаем следующую формулу:
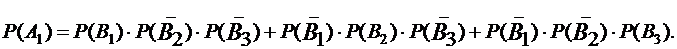
По условию
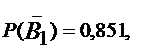
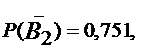
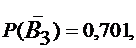
а по формуле 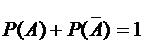 получаем
получаем
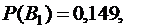
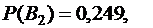
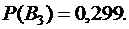
Таким образом,
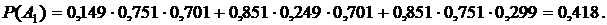
6) A2 - за время T выходит из строя хотя бы один элемент.
Событие определяется словами «хотя бы один», значит используем противоположное событие.
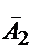 - за время T все элементы работают безотказно:
- за время T все элементы работают безотказно:
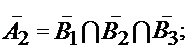
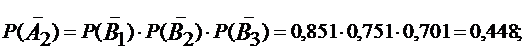
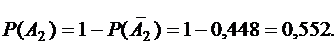
Ответ: P(A1) = 0,418, P(A2) = 0,552.
Задача 1.6.
В первой урне 6 белых и 4 черных шара, а во второй урне 5 белых и 7 черных шаров. Из первой урны взяли случайно 3 шара, а из второй -2 шара. Найти вероятность того, что среди вынутых шаров:
а) все шары одного цвета;
б) только три белых шара;
в) хотя бы один белый шар.
|
 Шары вынимали из обеих урн независимо. Испытаниями являются извлечение трех шаров из первой урны и двух шаров из второй урны. Элементарными событиями будут сочетания по 3 или 2 из 10 или 12 шаров соответственно.
Шары вынимали из обеих урн независимо. Испытаниями являются извлечение трех шаров из первой урны и двух шаров из второй урны. Элементарными событиями будут сочетания по 3 или 2 из 10 или 12 шаров соответственно.
а) A1 - все вынутые шары одного цвета, т е. они или все белые, или все черные.
Определим для каждой урны всевозможные события:
B1 - из первой урны вынуты 3 белых шара;
B2 - из первой урны вынуты 2 белых и I черный шар;
B3 - изпервой урны вынуты 1 белый к 2 черных шара;
B4 - из первой урны вынуты 3 черных шара,
C1 - из второй урны вынуты 2 белых шара;
C2 - из второй урны вынуты 1 белый и 1 черный шар;
C3 - из второй урны вынуты 2 черных шара.
Значит, 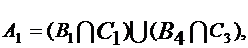 откуда, учитывая независимость и несовместимость событий, получаем
откуда, учитывая независимость и несовместимость событий, получаем
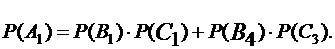
Найдем количество элементарных событий n1 и n2 для первой и второй урн соответственно. Имеем
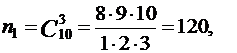
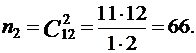
Найдем количество каждого из элементарных событий, определяющих следующие события:
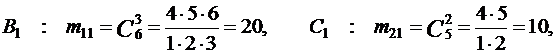
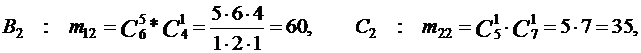
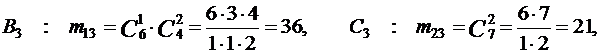
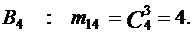
Следовательно,
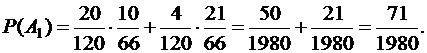
6) A2 - среди извлеченных шаров только 3 белых. В этом случае
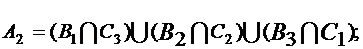
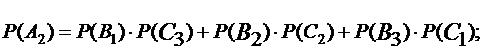
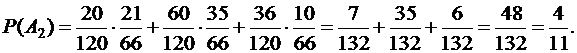
в) A3 - среди извлеченных шаров имеется по крайней мере один белый.
 - среди извлеченных шаров нет ни одного белого шара.
- среди извлеченных шаров нет ни одного белого шара.
Тогда
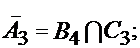
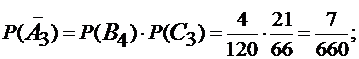
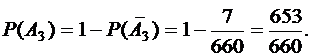
Ответ: P(A1) = 71/1980, P(A2) = 4/11, P(A3) = 653/660.
Задача 1.7.
В урне 4 черных и белых шара. К ним прибавляют 2 белых шара. После этого из урны случайным образом вынимают 3 шара. Найти вероятность того, что все вынутые шары белые, предполагая, что все предположения о первоначальном содержании урны равновозможны.
Здесь имеют место два вида испытаний: сначала задается первоначальное содержимое урны и затем случайным образом вынимается 3 шара, причем результат второго испытания зависит от результата первого. Поэтому используем формулу полной вероятности 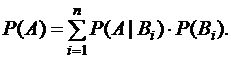
Событие A - случайно вынимают 3 белых шара. Вероятность этого события зависит от того, каким был первоначальный состав шаров в урне.
Рассмотрим события:
B1 - в урне было 4 белых шара;
B2 - в урне было 3 белых и 1 черный шар;
B3 - в урне было 2 белых и 2 черных шара;
B4 - в урне был 1 белый и 3 черных шара;
B5 - в урне было 4 черных шара.
Формулу полной вероятности используем в следующем виде:
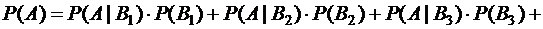
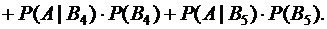
События B1, B2 , B3 , B4 , B5 образуют полную систему событий, значит, их сумма равна достоверному событию
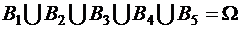
Используя формулу (1.3), получаем
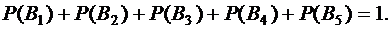
По условию все эти вероятности равны. Следовательно,
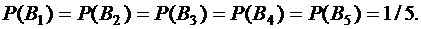
Общее число элементарных исходов
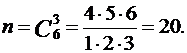
Найдем условные вероятности события А при различных условиях.

При B1 : 

При В2: 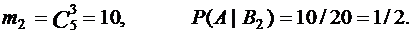

При В3 : 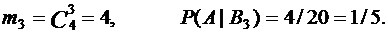
При В4 : 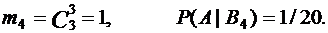
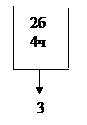
При В5 : 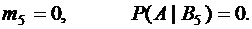
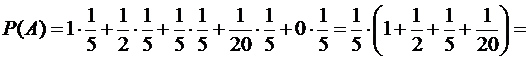
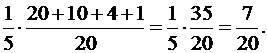
Ответ: Р(А) = 7/20.
Задача 1.8.
В одной урне 5 белых и 6 черных шаров, а в другой - 4 белых 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.
|
В этой задаче испытания также происходят в два этапа: вначале случайным образом вынимают шары из первой урны и опускают во вторую, а затем случайно вынимают шары из второй урны. Рассмотрим события:
А — шары, взятые из второй урны;
B1 - из первой урны взяли 3 белых шара;
B2 - из первой урны взяли 2 белых и 1 черный шар;
B3 - из первой урны взяли 1 белый и 2 черных шара;
B4 - из первой урны взяли 3 черных шара.
Используя формулу полной вероятности 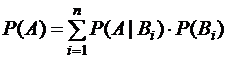 , находим
, находим
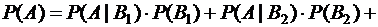
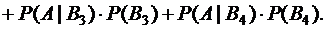
Количество элементарных событий на первом этапе равно
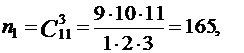
а на втором этапе
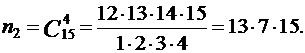
При B1 : 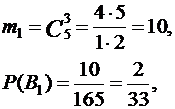
| 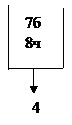
| 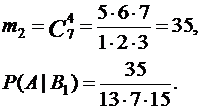
|
При В2 : 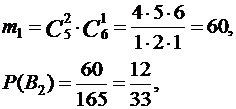
| 
| 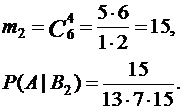
|
При В3 : 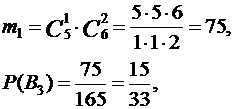
| 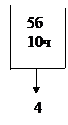
| 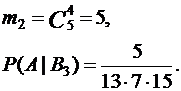
|
При B4 : 
| 
| 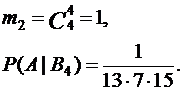
|
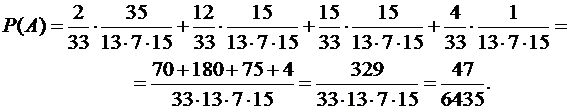
Ответ: Р{А) = 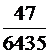 .
.
Задача 1.9.
В пирамиде стоят 19 винтовок, из них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0,81, а стреляя из винтовки без оптического прицела, - с вероятностью 0,46. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
В этой задаче первым испытанием является случайный выбор винтовки, вторым - стрельба по мишени. Рассмотрим следующие события:
А - стрелок поразит мишень;
B1 - стрелок возьмет винтовку с оптическим прицелом;
B2 - стрелок возьмет винтовку без оптического прицела.
Используем формулу полной вероятности 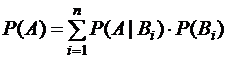 .
.
Имеем
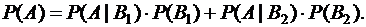
Учитывая, что винтовки выбираются по одной, получаем 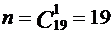 и соответственно
и соответственно 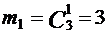 (для B1) и
(для B1) и 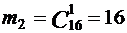 (для B2); таким образом, P(B1) = 3/19, P(B2) = 16/19.
(для B2); таким образом, P(B1) = 3/19, P(B2) = 16/19.
Условные вероятности заданы в условии задачи:
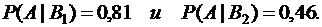
Следовательно,
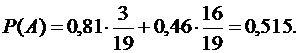
Ответ: Р(А)= 0,515.
Задача 1.10.
В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19, 6 и 11 шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71. Рабочий берет случайно один двигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен третьим заводом - изготовителем.
Первым испытанием является выбор электродвигателя, вторым - работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:
А - электродвигатель работает безотказно до конца гарантийного срока;
B1 - монтер возьмет двигатель из продукции 1-го завода;
B2 - монтер возьмет двигатель из продукции 2-го завода;
B3 - монтер возьмет двигатель из продукции 3-го завода.
Вероятность события А вычисляем по формуле полной вероятности:
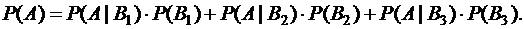
Условные вероятности заданы в условии задачи:

Аналогично предыдущей задаче найдем вероятности:
P(B1) = 19/36 = 0,528; P(B2) = 6/36 = 0,167; P(B3) = 11/36 = 0,306;.
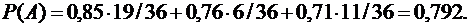
По формуле Бейеса 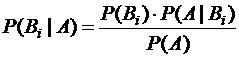 вычисляем вероятность того, что работающий безотказно двигатель поставлен третьим заводом-изготовителем
вычисляем вероятность того, что работающий безотказно двигатель поставлен третьим заводом-изготовителем
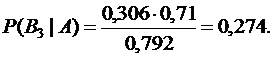
Ответ: Р(B3 | A ) = 0,274.
Задач 2.1.
В каждом из 11 независимых испытаний событие А происходит с постоянной вероятностью 0,3. Вычислить все вероятности pk , k = 0, 1, 2, ..., 11, где k - частота события А. Построить график вероятностей pk.. Вычислить наивероятнейшую частоту.
Задано: n = 11, p = 0,3, q = 1 – p = 0,7.
Найти: p0 , p1 , p2 ,…, p11 и k.
Используем формулу Бернулли 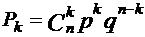 и формулу
и формулу 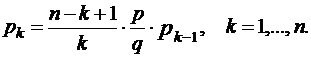
Значение p0 вычисляем по первой из формул, а остальные вероятности pk - по второй.
Для формулы 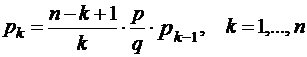 вычисляем постоянный множитель:
вычисляем постоянный множитель:
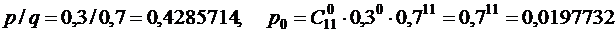 .
.
Результаты вычислений запишем в табл. 5. Если вычисления верны, то должно выполняться равенство 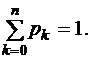
По найденным значениям вероятностей построим их график (рис. 1.).
Найдем наивероятнейшую частоту по заданным условиям:

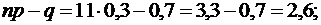

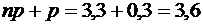 .
.
Получим 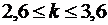 .
.
Так как 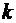 - целое число, то искомая наивероятнейшая частота
- целое число, то искомая наивероятнейшая частота 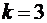 и значение
и значение 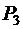 является максимальным.
является максимальным.
Таблица 5
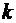
| 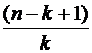
| 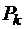
| 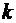
| 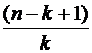
| 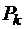
|
| 0 | - | 0,0197732 | 6 | 6/6 | 0,0566056 |
| 1 | 11/1 | 0,0932168 | 7 | 5/7 | 0,0173282 |
| 2 | 10/2 | 0,1997503 | 8 | 4/8 | 0,0037131 |
| 3 | 9/3 | 0,2568218 | 9 | 3/9 | 0,0005304 |
| 4 | 8/4 | 0,2201330 | 10 | 2/10 | 0,0000454 |
| 5 | 7/5 | 0,1320798 | 11 | 1/11 | 0,0000017 |
| ∑ | - | 0,9999994 |
Задача 2.2.
В каждом из 700 независимых испытаний событие А происходит с постоянной вероятностью 0,35. Найти вероятность того, что событие А происходит:
а) точно 270 раз;
б) меньше чем 270 и больше чем 230 раз;
в) больше чем 270 раз.
Учитывая, что количество испытаний n = 700 довольно велико, можно использовать формулы Муавра – Лапласа
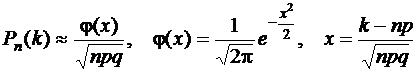 и
и 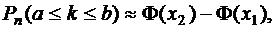 где
где
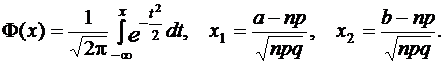
а) Задано: n = 700, p = 0,35, k = 270.
Найти: P700(270).
Используем локальную теорему Муавра-Лапласа (формула 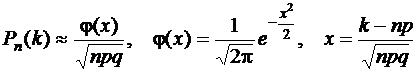 )
)
Находим:
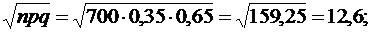
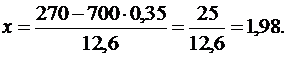
Значение функции 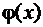 найдем из таблицы (см. приложение 6):
найдем из таблицы (см. приложение 6):
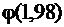 = 0,0562, Р700(270) =
= 0,0562, Р700(270) = 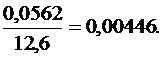
б) Задано: n = 700, p = 0,35, a = 230, b = 270.
Найти: P700(230<k<270).
Используем интегральную теорему Муавра-Лапласа
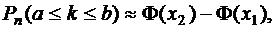 где
где
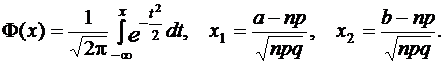
Находим:
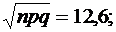
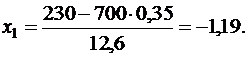
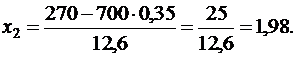
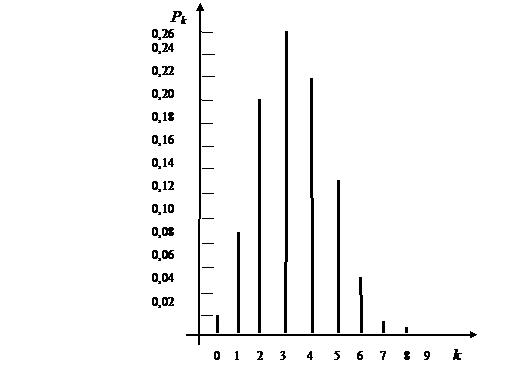
Рис. 1. График вероятностей pk к задаче 2.1.
Значение функции 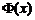 найдем из таблицы (см. приложение 7):
найдем из таблицы (см. приложение 7):
P700(230<k<270) = Ф(1,98) – Ф(-1,19) = Ф(1,98) + Ф(1,19) = 0,4761 + 0,3830 = 0,8591.
в) Задано: n = 700, p = 0,35, a = 270, b = 700.
Найти: P700(270<k).
Имеем: 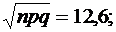
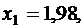
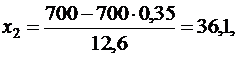
P700(270<k) = P700(270<k<700) = Ф(36,1) – Ф(1,98) =
=0,5 – 0,4761 = 0,0239.
Задача 2.3.
В каждом из 500 независимых испытаний событие А происходит с постоянной вероятностью 0,4. Найти вероятность того, что событие А происходит:
а) точно 220 раз;
б) точно 190 раз;
в) меньше чем 240 и больше чем 180 раз;
г) меньше чем 235 раз.
При решении этой задачи используем теоремы Муавра – Лапласа: локальную в случаях а) и б) и интегральную для случаев в) и г).
а) Задано: n = 500, p = 0,4, k = 220.
Найти: P500(220).
Имеем:

б) Задано: n = 500, p = 0,4, k = 190.
Найти: P500(190).
Получаем:
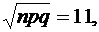
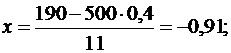
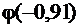 = 0,26369, Р500(190) =
= 0,26369, Р500(190) = 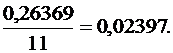
в) Задано: n = 500, p = 0,4, a = 180, b = 240.
Найти: P500(180<k<240).
Находим:
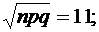
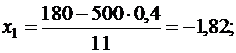
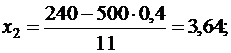
P500(180<k<240) = Ф(3,64) – Ф(-1,82) = Ф(3,64) + Ф(1,82) = =0,4999 + 0,4656 = 0,9655.
г) Задано: n = 500, p = 0,4, a = 0, b = 235.
Найти: P500(k<235).
Имеем:
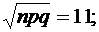
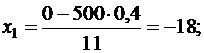
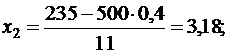
P500(k<235) = P500(0<k<235) = Ф(3,18) – Ф(-18) =
=Ф(3,18) + Ф(18) = 0,4993 + 0,5 = 0,9993.
Задача 2.4.
На телефонной станции неправильное соединение происходит с вероятностью 1/200. Найти вероятность того, что среди 200 соединений произойдет:
а) точно 1 неправильное соединение;
б) меньше чем 3 неправильных соединения;
в) больше чем 2 неправильных соединения.
Здесь вероятность события мала, поэтому используем формулу Пуассона:
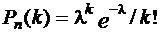 , где
, где 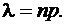
а) Задано: n = 200, p = 1/200, k = 1.
Найти: P200(1).
Получаем:
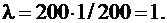
Определяем вероятность:
P200(1) = 0,3679.
б) Задано: n = 200, p = 1/200, k < 3.
Найти: P200(k < 3).
Имеем:
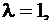
P200(k < 3) = P200(0) + P200(1) + P200(2) = 0,3679 + 0,3679 + 0,1839 = =0,9197.
в) Задано: n = 200, p = 1/200, k > 2.
Найти: P200(k > 2).
Находим: 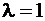 .
.
Эту задачу можно решить проще, если найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем:
P200(k > 2) = 1- P200(k 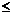 2) = 1 - P200(k < 3) = 1 – 0,9197 = 0,0803.
2) = 1 - P200(k < 3) = 1 – 0,9197 = 0,0803.
Задача 2.5.
В каждом из 600 независимых испытаний событие А происходит с постоянной вероятностью 0,85. Найти вероятность того, что относительная частота k/600 этого события по абсолютной величине от вероятности 0,85 не больше чем на 0,0055.
Задано: n = 600, p = 0,85, ε1= 0,0055.
Найти: P600 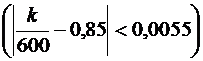 .
.
Воспользуемся формулой
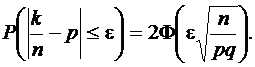
Искомая вероятность
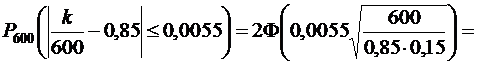
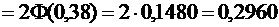
Задача 2.6.
Случайная величина Х задана рядом распределения
| Х | 3 5 7 11 |
| Р | 0,14 0,20 0,49 0,17 |
Найти функцию распределения F(x) случайной величины Х и построить ее график. Вычислить для Х математическое ожидание М(Х) и дисперсию D(X).
Функцию распределения для дискретных случайных величин находим по формулам 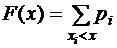 и
и
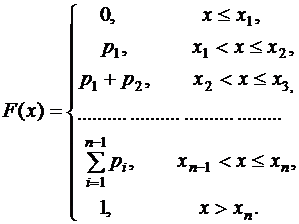
Искомая функция распределения имеет вид:
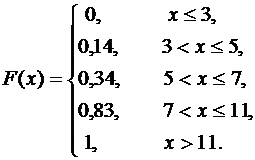
Построим график функции распределения F(x) (рис. 2). Математическое ожидание М(Х) вычисляем по формуле: 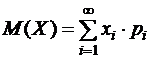
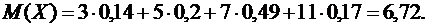
Для нахождения дисперсии воспользуемся формулами: 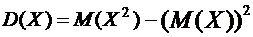 и
и 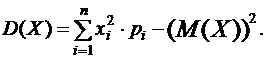
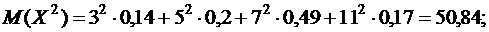
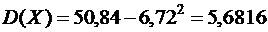

Рис. 2. График функции распределения к задаче 2.6.
Задача 2.7.
Случайная величина Х задана функцией плотности вероятности
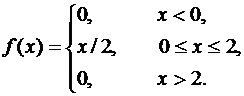
Найти функцию распределения F(x) случайной величины Х. Построить графики функций f(x) и F(x). Вычислить для Х ее математическое ожидание М(Х) и дисперсию D(X).
Функцию распределения F(x) случайной величины найдем по формуле 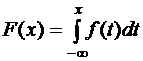 :
:
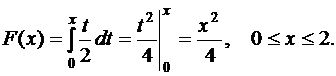
Поэтому
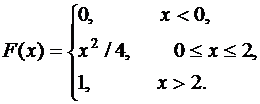
Построим графики функций f(x) и F(x) (рис. 3 и 4). Математическое ожидание вычисляем по формуле 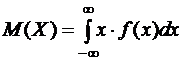 :
:
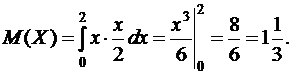
Для нахождения дисперсии Х воспользуемся формулами 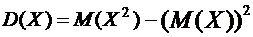 и
и 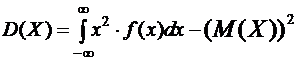 :
:
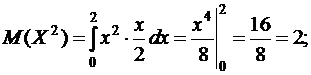
D(X) = 2 – (4/3)2 = 2 – 16/9 = 2/9.
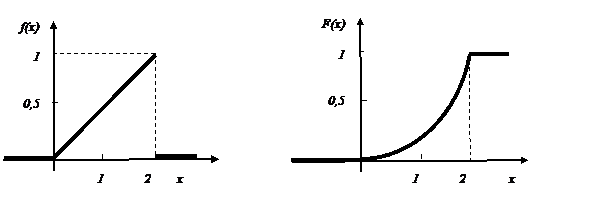 Рис. 3. График функции Рис. 4. График функции
Рис. 3. График функции Рис. 4. График функции
плотности вероятности f(x) распределения F(x)
Задача 2.8.
Случайная величина Х задана функцией распределения
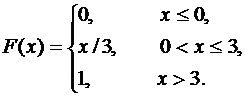
Найти функцию плотности вероятности f(x) случайной величины Х. Построить графики функций f(x) и F(x). Вычислить для Х ее математическое ожидание М(Х) и дисперсию D(X).
Функцию плотности вероятности вычислим по формуле f(x) = F'(x), дальнейшее решение задачи аналогично решению предыдущей задачи.
Задача 2.9.
Задана случайная величина x 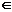 N (0, 2). Найти вероятность того, что эта случайная величина принимает значение:
N (0, 2). Найти вероятность того, что эта случайная величина принимает значение:
а) в интервале [-1, 2];
б) меньшее -1;
в) большее 2;
г) отличающееся от своего среднего значения по абсолютной величине не больше чем на 1.
В первых трех случаях можно воспользоваться формулой 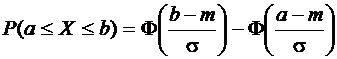 , а четвертом – формулой
, а четвертом – формулой 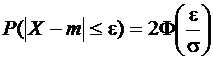 .
.
а) Задано: т =0, σ = 2, a = -1, b = 2.
Найти: 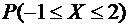 .
.
Имеем:
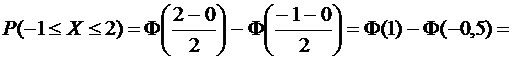
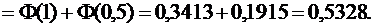
б) Задано: т =0, σ = 2, a = - 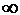 , b = -1.
, b = -1.
Найти: 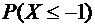 .
.
Получаем:
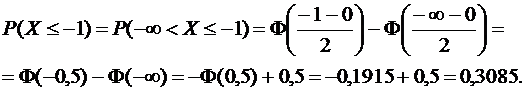
в) Задано: т =0, σ = 2, a = 2, b = 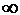 .
.
Найти: 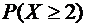 .
.
Имеем:
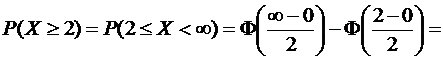
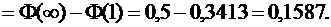
г) Задано: т =0, σ = 2, ε = 1.
Найти: 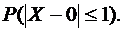
Получаем:
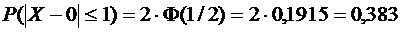 .
.
Задача 2.10.
Задана случайная величина Х 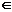 N (-10, 3) и точки -17, -13, -7, -1, 2 на числовой оси, разделяющие ее на шесть интервалов. Найти вероятность того, что эта случайная величина Х принимает значения в этих интервалах.
N (-10, 3) и точки -17, -13, -7, -1, 2 на числовой оси, разделяющие ее на шесть интервалов. Найти вероятность того, что эта случайная величина Х принимает значения в этих интервалах.
Используем формулу 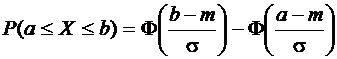 . Учитывая, что конец одного интервала является началом следующего, записываем результаты вычислений в таблице
. Учитывая, что конец одного интервала является началом следующего, записываем результаты вычислений в таблице
(табл. 6).
Таблица 6
| xi | 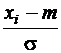
| 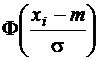
| 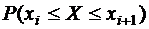
|
- 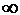
| - 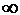
| -0,5000 | 0,0099 |
| -17 | -2,33 | -0,4901 | 0,1488 |
| -13 | -1 | -0,3413 | 0,6826 |
| -7 | 1 | 0,3413 | 0,1573 |
| -1 | 3 | 0,49865 | 0,00132 |
| 2 | 4 | 0,499968 | 0,00003 |
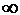
| 
| 0,5000 |
Интервалы охватывают всю числовую ось, так что сумма полученных вероятностей должна быть равна 1.
Контрольная домашняя работа
Задания для контрольной работы. Контрольная работа содержит 5 заданий : задание № 3 - № 7. В каждом задание содержится 30 задач , пронумерованных двумя цифрами.
Первая цифра означает номер задания , вторая – номер варианта.
Задание № 3
3.1. По движущейся цели производится три выстрела. Вероятность попадания при первом выстреле равна 0,2, при каждом из последующих она увеличивается на 0,1. Определить вероятность, получить: а) три промаха; б) хотя бы одно попадание.
3.2. На огневом рубеже находятся четыре стрелка. Вероятность попадания в “десятку” при одном выстреле каждым из них соответственно равны 0,2; 0,5; 0,4; 0,7. Найти вероятность того, что при одном выстреле: а) каждый из четырех стрелков попадет в десятку; б) будет хотя бы одно попадание в “десятку”.
3.3. При увеличении напряжения в два раза может произойти разрыв цепи вследствие выхода из строя любого из трех элементов с вероятностями соответственно 0,3, 0,4, 0,6. Определить вероятность того, что при увеличении напряжения в два раза не будет разрыва цепи.
3.4. Для взрыва склада боеприпасов достаточно одного попадания. По складу боеприпасов производится три выстрела. Вероятности попадания в склад при первом, втором и третьем выстрелах соответственно равны 0,2, 0,3, 0,4. Найти вероятность того, сто склад будет взорван.
3.5. Два штурмовика одновременно атакуют ракетную пусковую установку: вероятность попадания в пусковую установку после атаки первого штурмовика равна 0,4, после атаки второго 0,3. определить вероятность: а) одного попадания; б) двух попаданий; в) хотя бы одного попадания.
3.6. Производится три выстрела по движущейся цели. Вероятность попадания при первом выстреле равна 0,6, при втором 0,75, при третьем 0,8. определить вероятность: а) трех попаданий в цель; б) хотя бы одного попадания в цель.
3.7. На трех этапах подготовки изделия к функционированию вероятности появления задержек соответственно равны 0,1, 0,06 и 0,05. Найти вероятность подготовки изделия к работе без задержек.
3.8. В студии телевидения имеется три телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент: а) включена хотя бы одна камера; б) включены все три камеры.
3.9. Вероятность того, что студент сдаст экзамен на “отлично”, равна 0,1, на “хорошо” – 0,2, на “удовлетворительно” – 0,3. Определить вероятность того, что студент сдаст экзамен.
3.10. В ящике 10 деталей, среди которых 2 нестандартные. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной нестандартной детали.
3.11. На стеллаже библиотеки в случайном порядке расставлены 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.
3.12. Рабочий обслуживает 4 станка. Вероятность того, что в течении часа первый станок не требует внимания рабочего, равна 0,3, второй – 0,4, третий – 0,7, четвертый – 0,4. Найти вероятность того, что в течение часа: а) ни один станок не потребует внимания рабочего; б) хотя бы один потребует внимания рабочего.
3.13. В мешке смешаны нити, среди которых 30% белых, а остальные красные. Определить вероятность того, что вынутые наудачу две нити будут одного цвета.
3.14. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 – для второго. Найти вероятность того, что при аварии сработает: а) только один сигнализатор; б) хотя бы один сигнализатор.
3.15. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,8. Найти вероятность того, что из двух проверяемых изделий: а) только одно стандартно; б) хотя бы одно стандартно.
3.16. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.
3.17. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий будет только два изделия высшего сорта.
3.18. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочнике, соответственно равны 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится: а) только в одном справочнике; б) только в двух справочниках; в) во всех справочниках.
3.19. Вероятность того, что нужная сборщику деталь содержится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятность того, что деталь содержится: а) не более чем в трех ящиках; б) не менее чем в двух ящиках.
3.20. Брошены три игральные кости. Найти вероятности следующих событий: а) на каждой из выпавших граней появится 5 очков; б) на всех выпавших гранях появится одинаковое число очков.
3.21. В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в переплете. Библиотекарь взял 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете.
3.22. В цехе работает 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
3.23. Вероятность того, что в определенный день торговой базе потребуется двухтонная машина, равна 0,9, пятитонная – 0,7. Определить вероятность того, что торговой базе потребуется хотя бы одна автомашина (двухтонная или пяти тонная).
3.24. В приемнике радиосвязи с маневровым локомотивом имеется 6 ламп первого типа и 8 ламп второго типа. Вероятность выхода из строя в течение смены лампы первого типа – 0,002, а второго типа – 0,004. Определить вероятность выхода из строя приемника (в результате выхода из строя хотя бы одной лампы).
3.25. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первый получает приз. Найти вероятность того, что стрелки получат приз.
3.26. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него будет сброшены 4 бомбы с вероятностями попадания, соответственно равными 0,3; 0,4; 0,6; 0,7.
3.27. Достаточным условием сдачи коллоквиума является ответ на один из двух вопросов, предлагаемых преподавателем студенту. Студент не знает ответов на 8 вопросов из 40, которые могут быть предложены. Какова вероятность, что студент сдаст коллоквиум?
3.28. В ящике 10 красных, 6 синих и 4 зеленых шаров. Наудачу вынимают 2 шара. Какова вероятность того, что оба шара окажутся одного цвета?
3.29. На складе находятся 100 одинаковых коробок с обувью. Коробки не рассортированы по цвету. Известно, что в 60 коробках обувь черного цвета и в 40 – коричневого. Найти вероятность того, что из 5 наудачу взятых коробок окажутся 3 коробки с обувью черного и 2 коробки с обувью коричневого цвета.
3.30. Игра состоит в набрасывании колец на колышек. Игрок получает 6 колец и бросает кольца до первого попадания. Вероятность попадания при каждом броске равна 0,1. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным.
Задание № 4
4.1. Торпедный катер атакует корабль противника, выпуская по нему одну торпеду. Вероятность попадания торпеды в носовую часть корабля равна 0,2, в среднюю 0,3, в кормовую 0,15. Вероятность потопления корабля при попадании торпеды в носовую часть равна 0,45, в среднюю 0,9, в кормовую 0,5. Определить вероятность потопления корабля противника.
4.2. По цели производится два одиночных выстрела. При одном попадании цель выходит из строя с вероятностью 0,5, при двух с вероятностью 0,8. Вероятность попадания в цель при первом выстреле равна 0,6, при втором 0,7. Найти вероятность того, что в результате двух выстрелов цель будет выведена из строя.
4.3. Элементы, изготовленные на предприятии, поступают на склад готовой продукции. Предприятие, которое выпускает годную продукцию с вероятностью 0,98, поставило на склад три четверти от общего объема продукции, находящейся на складе. Предприятие, которое выпускает годную продукцию с вероятностью 0,96, поставило на склад остальную часть продукции, находящуюся на складе. Найти вероятность того, что полученный со склада элемент окажется годным.
4.4. Пиропатроны поставляются тремя заводами. Первый завод поставляет 50%, второй 30%, третий 20% всей продукции. Вероятность изготовления исправного пиропатрона заводами соответственно равны: 0,4; 0,8; 0,9. Найти вероятность того, что выбранный наугад для испытаний пиропатрон исправен.
4.5. В трех урнах находятся белые и черные шары. Первая урна содержит три белых шара и один черный, вторая – шесть белых и четыре черных, третья – девять белых и один черный. Из урны, выбранной наугад, вынимают шар, который оказывается белым. Найти вероятность того, что шар вынут из второй урны, если выбор любой из урн одинаково возможен.
4.6. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 легкоатлета. Вероятность пройти тестирование с положительным результатом для лыжника – 0,9, для велосипедиста – 0,8 и для легкоатлета 0,75. Найти вероятность того, что спортсмен, вызванный случайным образом, пройдет тестирование с положительным результатом.
4.7. Электрические приборы поставляются в магазин двумя заводами. Первый завод поставляет 60%, второй – 40% приборов. Вероятности изготовления заводами прибора, отвечающего установленным требованиям, соответственно равны: 0,95, 0,8. Найти вероятность того, что купленный стандартный прибор изготовлен первым заводом.
4.8. В зоне стрельбы находятся четыре крупных цели, пять средних и одиннадцать мелких. Вероятность попадания в цель каждого типа при стрельбе соответственно равны: 0,8, 0,2, 0,1. Определить вероятность попадания в цель при одном выстреле.
4.9. Рассматривается пять одинаковых урн. Две урны относятся к первому составу и содержат по три белых и два черных шара. Две другие урны относятся ко второму составу и содержат по четыре белых и шесть черных шаров, одна урна принадлежит к третьему составу и содержит восемь белых и два черных шара. Из одной урны, наугад выбранной урны, вынимают шар, который оказывается белым. Найти вероятность того, что шар взят из урны: а) первого состава; б) второго состава; в) третьего состава.
4.10. В учебной группе 25 студентов, из них 7 учатся отлично, 10 – хорошо, 6 - удовлетворительно и 2 – неудовлетворительно. Вероятность того, что на экзамене ответит неудовлетворительно отличник, равна 0,05, студент, учащийся на хорошо, - 0,15, студент, учащийся на удовлетворительно, - 0,3, студент, учащийся на неудовлетворительно – 0,8. Найти вероятность того, что вызванный случайным образом из состава группы студент получит при ответе неудовлетворительную оценку.
4.11. На складе находится четыре монитора. Вероятность того, что монитор выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый случайным образом монитор выдержит гарантийный срок службы.
4.12. По цели производится два независимых одиночных выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6. При одном попадании цель выходит из строя с вероятностью 0,7, при двух – с вероятностью 1,0. Найти вероятность того, что в результате двух выстрелов цель будет выведена из строя.
4.13. Сборщик получил три коробки деталей, изготовленных заводом №1, и две коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,8, а завода №2 - 0,9. Сборщик случайным образом извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
4.14. Для проведения стрельбы прибыло 10 стрелков, из которых четверо всегда выполняли упражнения, пятеро выполняли упражнение в 80% случаев и один выполнял упражнение в половине случаев. Найти вероятность того, что вызванный случайным образом стрелок выполнит упражнение.
4.15. Трое спортсменов одновременно выстрелили по движущейся мишени, в результате чего мишень была поражена одной пулей. Определить вероятность того, что мишень была поражена первым, вторым, третьим спортсменом, если вероятности попаданий для них равны соответственно 0,1; 0,4; 0,8.
4.16. В каждый момент времени работает только один из трех блоков агрегата. Наблюдение установило, что блок №1 работает 40% времени, блок №2 – 35% и блок №3 – 25%. Вероятность безотказной работы блоков за время T соответственно равны 0,95; 0,92; 0,9. Агрегат останавливается при отказе блока, находящегося под нагрузкой. Найти вероятность того, что агрегат остановится в случайно выбранный момент времени.
4.17. Данный тип деталей изготовляется на трех станках-автоматах, производительности которых относятся как 2:3:4. Первый автомат дает 15% брака, второй – 0,8% и третий – 0,5%. На контроле первая деталь оказалась бракованной. Найти вероятность того, что деталь изготовлена на первом станке.
4.18. По цели производится два выстрела. Вероятность попадания в цель при первом выстреле равна 0,4, при втором – 0,7. При одном попадании цель поражается с вероятностью 0,5, при двух – с вероятностью 0,9. Определить вероятность поражения цели.
4.19. Детали, предназначенные для контроля, находятся в десяти одинаковых ящиках. В девяти ящиках содержится по две бракованных и по две качественных детали, а в одном – четыре качественных и одна бракованная деталь. Найти вероятность того, что деталь извлечена из ящика, содержащего четыре качественных делали, если ящик проверки был выбран случайным образом и извлеченная деталь оказалась качественной.
4.20. Два самолета производят бомбометание по заданной цели. Каждый самолет сбрасывает одну бомбу. Вероятность попадания в цель при сбрасывании одной бомбы для первого самолета равна 0,3, для второго – 0,5. По итогам бомбометания цель была поражена одной бомбой. Найти вероятность того, что в цель попала бомба, сброшенная с первого самолета.
4.21. В тире имеется 9 ружей, из которых пристрелянными являются два. Вероятность попадания в цель из пристрелянного ружья 0,8, а из непристрелянного – 0,1. Выстрелом из одного, случайным образом взятого ружья, мишень была поражена. Найти вероятность того, что было взято пристрелянное ружье.
4.22. В группе шесть отличных стрелков, девять хороших, восемь посредственных и два плохих. Вероятность попадания в цель для отличного стрелка 0,9; для хорошего – 0,8; для посредственного – 0,5; для плохого – 0,1. На огневой рубеж случайным образом вызывается один стрелок из группы. Найти вероятность того, что он попадет в цель.
4.23. Штатный блок, установленный в аппаратуру связи, может принадлежать к одной из трех партий с вероятностями соответственно 0,35, 0,35, 0,3. Вероятность того, что установленный блок проработает заданное число часов, для этих партий равна соответственно 0,9, 0,8, 0,6. Найти вероятность того, что блок проработает заданное число часов.
4.24. В ящике содержится 12 деталей завода №1, 20 деталей завода №2, 18 деталей завода №3. Вероятность того, что деталь завода №1 отличного качества, равна 0,9; для деталей заводов №2 и №3 – соответственно 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
4.25. Два автомата производят одинаковые детали, которые сбрасываются на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что это деталь произведена первым автоматом.
4.26. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что эта машина грузовая.
4.27. На склад поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 46% и третьей – 34%. Известно также, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, а для третьей – 1%. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось нестандартным.
4.28. Имеется 10 одинаковых по виду урн, из которых в девяти находится по 2 черных и 2 белых шара, а в одной – 5 белых и 1 черный шар. Из наугад взятой урны извлечен шар. Чему равна вероятность того, что этот шар взят из урны, содержащей 5 белых шаров, если он оказался белым?
4.29. Некто заблудился в лесу, вышел на поляну, откуда вело 4 дороги. Известно, что вероятность выхода из леса за час для различных дорог, равны соответственно 0,6; 0,3; 0,2; 0,1. Чему равна вероятность того, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса через час?
4.30. Для сигнализации о том, что режим работы автоматической линии отклоняется от нормального, используется индикатор. Он принадлежит с вероятностями 0,2; 0,3; и 0,5 к одному из трех типов, для которых вероятности срабатывания при нарушении нормальной работы линии равны соответственно 1; 0,75 и 0,4. От индикатора получен сигнал. К какому типу вероятнее всего принадлежит индикатор?
Задание № 5
5.1. Производится пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,4. Найти вероятность того, что событие А наступит не менее трех раз.
5.2. Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено не более трех изделий.
5.3. Вероятность отказа любой из десяти независимо работающих систем агрегата за рассматриваемый период равна 0,2. Найти вероятность того, что за данный период откажут не более трех систем агрегата.
5.4. Всхожесть семян ржи составляет 90%. Чему равна вероятность того, что из семи посеянных семян взойдет пять?
5.5. Вероятность появления события В в любом из десяти испытаний равна 0,6. Найти вероятность того, что события В наступит не менее двух раз.
5.6. За рассматриваемый период времени среднее число ошибочных коммутаций, приходящееся на одного телефонного абонента, равно восьми.
Определить:
а) вероятность того, что для отдельно взятого абонента число ошибочных соединений будет не более двух;
б) вероятность того, что с данным абонентом не будет ни одного ошибочного соединения.
5.7. Прибор состоит из пяти независимо работающих блоков, вероятность отказа каждого из которых равна 0,3. Найти вероятность того, что число отказавших блоков не более двух.
5.8. Вероятность промаха при одном выстреле равна 0,016. Стрелок должен произвести по цели 500 выстрелов. Найти вероятность того, что он сделает не более трех промахов.
5.9. Вероятность того, что изделие не выдержит испытания, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытаний.
5.10. Вероятность попадания в цель при одном выстреле равно 0,8.
Определить вероятность получения ровно трех попаданий при трех выстрелах.
5.11. Найти вероятность того, что при 7 выстрелах будет от трех до шести попаданий включительно, если вероятность попадания при одном выстреле равна 0,7.
5.12. Производится стрельба по мишени. Вероятность попадания при одном выстреле равна 0,7, общее число выстрелов равно 10. Найти вероятность того, что мишень будет поражена не менее чем тремя выстрелами.
5.13. При передаче сообщения вероятность искажения одного знака равна 0,1. Какова вероятность того, что сообщение из 10 знаков содержит не более трех искажений.
5.14. Из каждого десятка деталей 9 – стандартные. Найти вероятность того, что из 50-ти взятых со склада деталей число стандартных окажется между 42 и 48.
5.15. Вероятность появления события в каждом из 100 испытаний равна 0,1. Найти вероятность того, что событие появится: а) не менее 14 раз; б) не более 14 раз.
5.16. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
5.17. Для некоторого стрелка вероятность попадания в мишень при одном выстреле равна 0,6. Произведено 100 выстрелов по мишени. Найти вероятность того, что число попаданий не менее 80 и не более 95.
5.18. Сто станков работают независимо друг от друга. Вероятность бесперебойной работы каждого из них в течение смены равна 0,8. Найти вероятность того, что в течение данной смены безотказно проработают 95 станков.
5.19. Найти вероятность того, что появление герба в 500 испытаниях будет не менее 200 и не более 300 раз.
5.20. Игральный шестигранный кубик подбрасывается 50 раз. Найти вероятность того, что цифра 6 выпадет: а) не менее 20-ти раз; б) не более 25-ти раз.
5.21. Вероятность появления события А в каждом опыте равна 0,3. Опыт повторяется 5 раз. Найти вероятность того, что событие А появится не более двух раз.
5.22. Найти вероятность того, что при пяти подбрасываниях шестигранного игрального кубика единица появится хотя бы один раз.
5.23. Вероятность изготовления бракованного генератора для автомобильного двигателя равна 0,0003. Найти вероятность того, что в изготовленной партии из 200 шт. окажется один бракованный.
5.24. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найти вероятность того, что из 1000 пассажиров опоздают к отправлению поезда не более двух.
5.25. При передаче сообщения вероятность искажения одного знака равна 0,01. Найти вероятность того, что при передаче сообщения из 100 знаков: а) не будет ни одного искажения; б) будет два искажения.
5.26. При установившемся технологическом процессе автомат производит 75% деталей первого сорта и 25% деталей второго сорта. Установить, что является более вероятным – получить 3 первосортных детали среди пяти случайным образом выбранных для проверки или 4 первосортных детали среди шести случайным образом выбранных для проверки.
5.27. На автобазе числится 6 автомашин. Вероятность выхода на линию каждой из них равна 0,9. Найти вероятность нормальной работы автобазы, если для этого необходимо, чтобы на линии было не менее пяти автомашин.
5.28. Вероятность прибытия поезда без опоздания равна 0,97. Считая опоздания отдельных поездов независимыми событиями, найти вероятность того, что из четырех выбранных поездов опоздает не более одного.
5.29. Средняя продолжительность безотказной работы устройства равна 1000 часам. Найти вероятность того, что за время 2000 часов будет не более пяти отказов.
5.30. На коммутатор поступает в среднем 1000 вызовов в час. Найти вероятность того, что в течение 10-ти минут поступит менее пяти вызовов.
Задание №6
6.1. В урне имеется 4 шара с номерами 1, 2, 3, 4. Вынули 2 шара. Найти математическое ожидание и дисперсию случайной величины Х – суммы номеров шаров.
6.2. Два стрелка делают по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,7, для второго – 0,9. Найти математическое ожидание и дисперсию числа попаданий в мишень.
6.3. В партии из 20 приборов имеется 6 неточных. Наудачу отобрали 4 прибора. Построить ряд распределения случайной величины Х – числа точных приборов среди отобранных. Найти 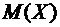 .
.
6.4. Охотник, имеющий 5 патронов, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле равна 0,4. Построить ряд распределения случайной величины X- числа израсходованных патронов. Найти 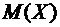 и
и 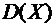 .
.
6.5. Производятся испытания пяти изделий на надежность. Вероятность выдержать испытание для каждого изделия равна 0,8. Построить ряд распределения случайной величины Х – числа изделий выдержавших испытания. Найти 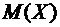 и
и 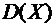 .
.
6.6. Среди поступивших в ремонт 10 часов в общей чистке нуждаются 6 штук. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в общей чистке, рассматривает из поочередно, и найдя их, прекращает просмотр. Составить закон распределения случайной величины Х – количество просмотренных часов и найти 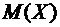 .
.
6.7. Вероятность попадания в мишень для данного стрелка 0,8. За каждое попадание стрелку зачисляется 5 очков. Составить таблицу распределения случайной величины Х – числа выбитых очков при 3 выстрелах. Построить график функции распределения 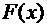 .
.
6.8. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны 3 детали. Найти закон распределения и функцию распределения случайной величины Х – числа стандартных деталей среди отобранных.
6.9. Вероятность попадания в мишень стрелком равна 0,7. Составить ряд распределения и функцию распределения случайной величины Х – числа попаданий в мишень стрелком при 4 выстрелах.
6.10. Устройство состоит из 3 независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить ряд распределения и найти функцию распределения числа отказавших элементов в одном опыте.
6.11. Монета бросается 3 раза. Случайная величина Х – число появлений герба. Найти 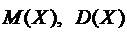 и
и 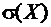 .
.
6.12. В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Найти закон распределения числа нестандартных деталей.
6.13. Стрелок делает по мишени 3 выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Найти закон распределения числа попаданий 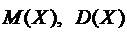 и
и 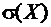 .
.
6.14. Баскетболист делает 4 броска мячом в корзину. Вероятность попадания мяча при одном броске равна 0,4. Найти математическое ожидание числа попаданий мячом к корзину.
6.15. Производится стрельба по мишени до первого попадания. Вероятность попадания равна 0,8. Имеется 4 снаряда. Найти математическое ожидание числа израсходованных снарядов.
6.16. Производится 5 независимых выстрелов по цели. Вероятность попадания при одном выстреле р=0,3. Найти: а) ряд распределения числа попаданий; б) вероятность того, что число попаданий менее 3.
6.17. В урне 6 белых и 4 черных шара. Из урны извлекается 5 раз подряд шар. Вынутый шар возвращается в урну и шары перемешиваются Случайная величина Х – число извлеченных белых шаров. Найти закон распределения, математическое ожидание и дисперсию случайной величины X.
6.18. Производится 5 независимых пусков ракет. Вероятность попадания в цель при каждом пуске равна р=0,6. Найти: а) ряд распределения числа попаданий; б) вероятность того, что число попаданий менее 3-х.
6.19. Стрелок производит 3 независимых выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. Найти математическое ожидание числа попаданий в мишень.
6.20. Построить ряд распределения и функцию распределения случайной величины Х – числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна р=0,3. Найти 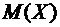 и
и 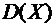 .
.
6.21. В урне 3 белых и 3 черных шара. Шары достаются по одному без возвращения до тех пор, пока не появится белый шар. Составить закон распределения случайной величины Х – числа проведенных испытаний. Найти 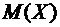 и
и 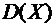 .
.
6.22. Найти математическое ожидание и дисперсию числа очков при одном бросании игральной кости.
6.23. В партии из 8 деталей – 5 стандартных. Наудачу отбирают 3 детали. Случайная величина Х – число стандартных деталей среди отобранных. Найти 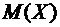 и
и 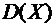 .
.
6.24. Опыт состоит из трех независимых бросаний монеты, при каждом из которых герб выпадает с вероятностью р=0,5. Для случайной величины Х – числа появлений герба, найти закон распределения и функцию распределения.
6.25. Две игральные кости одновременно бросают два раза. Случайная величина Х – число выпадений четного числа очков на двух костях одновременно. Найти закон распределения случайной величины Х, 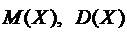 и
и 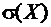 .
.
6.26. В партии из 6 деталей содержится 4 стандартных. Наудачу отобраны 3 детали. Найти закон распределения числа стандартных деталей среди отобранных.
6.27. В партии из 10 деталей содержится 3 стандартных. Наудачу отобраны 2 детали. Найти математическое ожидание дискретной случайной величины Х – числа нестандартных деталей среди двух отобранных.
6.28. В связке 5 ключей, из которых один подходит к двери. Дверь открывают путем опробований; опробованный ключ исключается. Составить закон распределения случайной величины Х – числа опробований. Найти 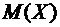 и
и 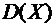 .
.
6.29. Производятся последовательные независимые испытания пяти приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Вероятность выдержать испытание для каждого прибора равна 0,9. Построить ряд распределения числа испытанных приборов.
6.30. Команда из 4 стрелков стреляет по одной мишени. Каждый стрелок делает по одному выстрелу. Вероятность попадания в мишень для одного стрелка 0,3, для другого – 0,4, для третьего и четвертого 0,5. Построить ряд распределения и функцию распределения общего числа попаданий в мишень командой.
Задание №7
7.1. Случайная величина X подчинена равномерному закону распределения на интервале от 1 до 2. Определить математическое ожидание и дисперсию случайной величины X.
7.2. Цена деления шкалы угломерного прибора равна 20-ти секундам. Показания прибора снимаются с округлением до целого деления шкалы. Определить среднее квадратическое отклонение случайной величины X – ошибки округления – и вероятность того, что ошибка округления не выйдет за пределы [0; 10] секунд.
7.3. Случайная величина X подчинена равномерному закону распределения с математическим ожиданием, равным трем, и средним квадратическим отклонением, равным 0,3. Найти плотность распределения случайной величины X.
7.4. Случайная величина Т – время работы прибора – подчиняется показательному распределению. Среднее время работы прибора 500 ч. Найти вероятность того, что время работы прибора будет не меньше 750ч.
7.5. Время работы радиотехнического устройства описывается функцией показательного распределения 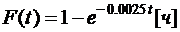 . Найти вероятность того, что время работы устройства не превысит его математическое ожидание.
. Найти вероятность того, что время работы устройства не превысит его математическое ожидание.
7.6. Случайная величина Y подчинена равномерному закону распределения на интервале от 2 до 5. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Y.
7.7. Случайная величина Т – время работы прибора – подчиняется экспоненциальному распределению. Среднее время работы прибора 300 ч. Найти вероятность того, что время работы прибора будет меньше 1000ч.
7.8. Время работы радиотехнического устройства описывается функцией показательного распределения 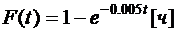 . Найти вероятность того, что время работы устройства превысит значение его математического ожидания.
. Найти вероятность того, что время работы устройства превысит значение его математического ожидания.
7.9. Высота подрыва заряда – случайная величина, подчиненная нормальному закону распределения с математическим ожиданием, равным 1200м, и среднеквадратическим отклонением, равным 100м. Найти вероятность подрыва заряда на высоте, превышающей 1000м.
7.10. Процент брака при изготовлении детали имеет нормальное распределение с математическим ожиданием, равным 1,5%, и средним квадратическим отклонением, равным 0,25%. Найти вероятность того, что процент брака проверяемой партии деталей лежит в пределах [1,5;2]%.
7.11. Колебания скорости летательного аппарата подчинены нормальному закону распределения. Среднее квадратическое отклонение скорости от своего расчетного значения равно 1,5 м/с. При превышении истинного значения скорости над расчетным более чем на 2,5 м/с, двигатель летательного аппарата выключается. Найти вероятность выключения двигателя.
7.12. Скорость летательного аппарата V измеряется при помощи некоторого прибора, ошибка измерения которого подчинена нормальному закону. Каким должно быть среднее квадратическое отклонение этой ошибки, чтобы в 95% всех измерений ошибка в скорости не превышала 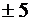 м/c.
м/c.
7.13. Случайная величина распределена нормально. Среднее квадратическое отклонение этой величины равно 0,4. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет меньше 0,3.
7.14. Температура в помещениях здания распределена по нормальному закону с параметрами 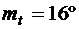 и
и 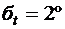 . Найти вероятность того, что значение температуры в помещении не менее
. Найти вероятность того, что значение температуры в помещении не менее 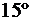 и не более
и не более 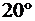 .
.
7.15. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины равны соответственно 6 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале [4;8].
7.16. Процент брака продукции распределен по нормальному закону со средним квадратическим отклонением 0,25% и математическим ожиданием 1,25%. Найти вероятность того, что в очередной партии продукции брак составит менее одного процента.
7.17. Случайная величина распределена нормально. Среднее квадратическое отклонение этой величины равно 0,1. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет не меньше единицы.
7.18. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины равны соответственно 10 и 0,2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале [5;11].
7.19. Случайная величина X распределена равномерно на интервале [0;2]. Найти математическое ожидание 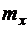 и дисперсию
и дисперсию 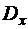 .
.
7.20. Случайная величина X распределена нормально с 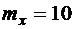 . Вероятность попадания в интервал [10;30] равна 0,3. Найти вероятность попадания случайной величины в интервал [0;10].
. Вероятность попадания в интервал [10;30] равна 0,3. Найти вероятность попадания случайной величины в интервал [0;10].
7.21. Случайная величина X распределена нормально с 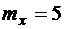 ,
, 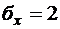 . Найти вероятность того, что
. Найти вероятность того, что 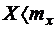 .
.
7.22. Случайная величина X распределена экспоненциально с параметром 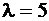 . Найти вероятность того, что
. Найти вероятность того, что 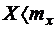 .
.
7.23. Случайная величина Z распределена нормально с 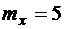 . Вероятность попадания в интервал [5;10] равна 0,4. Найти вероятность попадания случайной величины в интервал [0;5].
. Вероятность попадания в интервал [5;10] равна 0,4. Найти вероятность попадания случайной величины в интервал [0;5].
7.24. Случайная величина X задана плотностью распределения 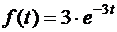 при
при 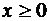 и
и 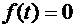 при
при 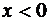 . Найти вероятность попадания случайной величины в интервал [1;3].
. Найти вероятность попадания случайной величины в интервал [1;3].
7.25. Функция распределения случайной величины X равна 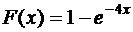 . Найти математическое ожидание
. Найти математическое ожидание 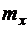 и дисперсию
и дисперсию 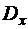 .
.
7.26. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины равны соответственно 0 и 1. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале [-2;2].
7.27. Случайная величина Х имеет нормальное распределение с параметром 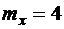 ,
, 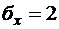 . Найти выражение плотности распределения и найти вероятность того, что Х примет значение, принадлежащее интервалу (-2;6).
. Найти выражение плотности распределения и найти вероятность того, что Х примет значение, принадлежащее интервалу (-2;6).
7.28. Случайная величина в интервале [0,3] задана плотностью распределения 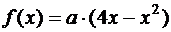 , вне этого интервала
, вне этого интервала 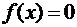 . Найти коэффициент
. Найти коэффициент 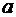 и
и 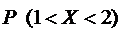 .
.
7.29. Непрерывная величина Х в интервале 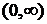 задана плотностью распределения
задана плотностью распределения 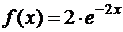 , вне этого интервала
, вне этого интервала 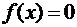 . Найти функцию распределения
. Найти функцию распределения 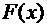 и вероятность того, что Х примет значение, принадлежащее интервалу (1;2).
и вероятность того, что Х примет значение, принадлежащее интервалу (1;2).
7.30. Случайная величина Х имеет плотность распределения 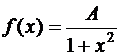 . Найти коэффициент А,
. Найти коэффициент А, 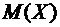 и
и 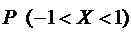 .
.
Дата добавления: 2018-02-15; просмотров: 1223; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
