Нормированная функция Лапласа. МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Тверской государственный технический университет»
(ГОУВПО ТвГТУ)
Математическая статистика
В машиностроении
Сборник задач
Тверь 2012
Сборник задач по дисциплине «Математическая статистика в машиностроении»: Г.Б. Бурдо, Г.И. Рогозин, Ф.Х.Арсланов. Тверь: ТГТУ, 2012 Г.
Представлены задачи по основным разделам дисциплины «Математическая статистика в машиностроении»: применение методов математической статистики для анализа точности механической обработки, настройки станков, контроля качества продукции и т. д.
Каждый тип задач сопровожден подробными методическими указаниями ирешением. Сборник задач предназначен для бакалавров, изучающих дисциплины ”Математическая статистика в технологии машиностроения” и «Теория вероятностей в технологии машиностроения» направлений 151900 и 227000 программы для высших учебных заведений.
УСЛОВИЯ ЗАДАЧ
Задача №1
Непрерывная случайная величина имеет следующее распределение:
| Интервалы Значений х | Середина
Интервала 
| Частота fi |
| 2-6 6-10 10-14 14-15 | 4 8 12 16 | 1 4 4 1 |
|
|
|
Определить среднее арифметическое 
и среднее квадратическое отклонение 
Задача № 2
По выборке объема п = 15 найдено X = 20,4 и s = 0,8. Определить истинное значение генеральной средней Х0.
Задача №3
Установить, какой объем n выборки необходимо взять, чтобы определить по этой выборке генеральную среднюю с точностью 
= ±2 
и
вероятностью 
= 0,95.
Задача №4
Определить точность приближенного равенства 0 
s с вероятностью
= 0,96, если n = 15 и s = 0,12.
Задача № 5
Определить п, при котором s будет отличаться от 0 на ±0,2 с вероятностью= 0,96.
Задача №6
Определить точность приближенного равенства 0 s с вероятностью = 0,95, если n = 50, s = 0,1.
Задача№7
Определить вероятность приближенного равенства 0 s, если n =50,
= 0,1.
Задача №8
Из текущей продукции автомата, обрабатывающего ролики D = 20_0)2 мм, была взята выборка объемом п = 100 шт. Ролики были измерены по диаметру микрометром с ценой деления 0,01 мм. Ниже приведены отклонения от номинального размера диаметра роликов в мм:
|
|
|
Определить статистические характеристики распределения, т. е. и s.
Задача№9
По данным примера 19 сопоставить эмпирическую кривую с теоретической кривой по закону нормального распределения и вычислить координаты характерных точек для построения теоретической кривой распределения.
Задача №10
Сопоставить эмпирическое распределение по данным задачи 8 с законом нормального распределения при помощи таблицы значений Ф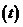 
.
Задача №11
По данным примеров 20 и 21 вычислить критерий 
и проверить гипотезу нормальности.
Задача№12
С автомата, обрабатывающего втулки D = 20мм, было взято в разное время две выборки по 5 шт. каждая. Результаты измерения диаметров втулок приведены в табл. ниже.
Распределение диаметров втулок предполагается нормальным.
Используя критерий t Стюдента показать, что настройка станка в момент взятия пробы №1 и №2 не изменилась.
Задача №13
При одних и тех же условиях было обработано по 25 шт. втулок разверткой d = 6 мм и разверткой d = 10 мм. Результаты измерений двух партий втулок показали, что средняя величина разбивки отверстий (разность между диаметром отверстия и диаметром развертки) составляет для d = 6 мм Х1=10,4 мкм, для d = 10 мм
|
|
|
Х2 =9,8 мкм. Дисперсии величин разбивок соответственно равны: 
= 3,8 мкм2 и 
= 4,76 мкм2.
Необходимо установить, влияет ли диаметр развертки на величину разбивки отверстий, если предварительными опытами установлено, что рассеивание величин разбивки подчиняется нормальному закону распределения.
Задача №14
С двух автоматов, обрабатывающих одинаковые детали, взято две выборки 
= п2 = 10. При этом оказалось, что = 400 мкм2 и
= 325 мкм2. Ранее было установлено, что рассеивание размеров деталей, обработанных на автоматах, следует нормальному закону распределения.
Можно ли считать, что оба станка обеспечивают одинаковую точность обработки?
Задача №15
С четырех автоматов, настроенных на обработку одних и тех же деталей, взято по одной текущей выборке объема п1 = п2 = п3 = n4 = 10. Дисперсии выборок имеют следующие значения: = 100 мкм2, = 300 мкм2, 
= 200 мкм2, 
= 400 мкм2. Требуется установить, одинакова ли точность автоматов, т. е. одинаково ли рассеивание случайных погрешностей обработки на этих автоматах, если предварительными исследованиями установлено, что это рассеивание подчиняется закону нормального распределения.
|
|
|
Задача №16
С двух станков, настроенных на обработку одной и той же детали, взяты текущие выборки объема n = m= 15. Результаты измерения деталей выборок приведены в табл., где через х обозначены отклонения измеряемого размера от номинала в мкм для выборки со станка № 1, а через у — отклонения в мкм измеряемого размера для выборки со станка № 2.
Требуется определить, можно ли считать точность обработки двух станков одинаковой. Другими словами, нужно проверить нулевую гипотезу о том, что распределения погрешностей обработки двух станков описываются одинаковыми функциями распределения.
Таблица
Результаты измерения деталей выборок
Задача № 17
Определить вероятность получения годовой продукции, если точность метода обработки w = 0,12 мм, а допуск 0,08 мм. Границы поля допуска относительно центра группирования расположены симметрично.
Задача № 18
Определить число годных деталей, исправимого и неисправимого брака при обработке партии валов 450 штук диаметром 40 - 0,16 мм, если вычисленные по результатам измерений пробных 50 деталей среднее квадратическое равно 0,03 мм, а смещение координаты середины поля допуска и центра группирования - 0,02 мм.
Задача №19
На токарном станке обрабатывают 300 валиков из стали 45. Размер заготовок d = 30 мм и l = 70 мм. Допуск на обработку 0,20 мм. Материал резца Т15К6. Режимы резания: V = 100 м/мин; S = 0,08 мм/об.; t = 0,5 мм. Определить количество годных и бракованных заготовок, если настройка станка обеспечивает симметричные расположения кривой распределения по отношению к полю допуска. По результатам замеров 75 штук пробных заготовок среднее квадратическое отклонение равно 0,02 мм.
Задача № 20
Определить возможность обработки без брака отверстия d = 50 + 0,20 мм, если:
а) по результатам пробной обработки среднее квадратическое отклонение равно 0,02 мм;
б) погрешности настройки 0,04 мм;
в) настройка производится без учета систематических закономерно изменяющихся погрешностей.
Задача № 21
Определить вероятность получения брака деталей, если точность метода обработки wобр = 0,12 мм, а допуск Т = 0,08 мм. Границы поля допуска расположены на расстоянии 0,03 и 0,05 мм от центра группирования.
Задача № 22
Определить процент брака по эксцентриситету между двумя шейками ступенчатого валика, если допуск на биение равен 0,08 мм. В результате непосредственных измерений 50 штук заготовок установлено, что среднее квадратическое отклонение эксцентриситета равно 0,008 мм.
Задача № 23
Обработка партии деталей в размер 60 +0,2 мм производится при нескольких настройках станка. Настройка станка производится без учета закономерно изменяющихся погрешностей. Погрешность настройки равна 0,05 мм. По результатам обработки пробной партии деталей среднее квадратическое отклонение равно 0,03 мм. Возможна ли принципиально обработка без брака?
Задача №24
Определить число годных деталей, исправимого и неисправимого брака при растачивании отверстий диаметром 130+0,1 мм в партии корпусных деталей 200 шт. Среднее квадратическое отклонение по результатам измерений 50 деталей составило 0,026 мм, и смещение кривой распределения размеров относительно середины поля допуска не происходит.
Задача № 25
По результатам пробной обработки установлено, что среднее квадратическое отклонение размера равно 0,04 мм. Погрешность метода настройки равна 0,05 мм. Настройка осуществляется при условии отсутствия систематических закономерно изменяющихся погрешностей. Определить, возможна ли обработка без брака партии валиков из 80 штук в диаметр 50 - 0,25 мм. Если брак неизбежен, то определить число бракованных деталей.
Задача № 26
На револьверном станке обрабатывают партию деталей 300 штук диаметром 30 - 0,1 мм. По результатам измерений 50 пробных деталей величины среднего и среднего квадратического отклонения составляют
29,97 мм и 0,019 мм соответственно. Определить число годных и бракованных деталей.
Задача № 27
Определить, возможна ли на токарном полуавтомате обработка валов диаметром 40 - 0,25 мм, если выборочное среднее и среднее квадратическое отклонения, вычисленные по результатам измерений 25 деталей, составили 39,88 мм и 0,025 мм соответственно.
Задача №28
Для расточки отверстия диаметром 60 + 0,1 мм в партии втулок из 200 штук на револьверном станке инструмент настраивается так, чтобы получаемый брак был исправим. Определить число деталей, требующих дополнительной обработки на более точном оборудовании, если предварительным статистическим анализом установлено, что среднее квадратическое отклонение равно 0,025 мм. Погрешность настройки принять равной 0,015 мм.
Задача № 29
Для обработки партии валов 300 штук диаметром 30 - 0,1 мм на револьверном станке инструмент настраивается так, чтобы получаемый брак был исправим. Определить число деталей, требующих дополнительной обработки на более точном оборудовании, если предварительным статистическим анализом установлено, что среднее квадратическое отклонение равно 0,025 мм. Погрешность настройки принять равной 0,02 мм.
Задача № 30
Рассчитать ординаты контрольных линий (с применением контрольных карт средних арифметических значений и размахов) процесса растачивания отверстий диаметром 130 + 0,1 мм в корпусных деталях, если предварительным статистическим анализом установлено, что среднее квадратическое отклонение равно 0,01 мм. Объем выборки установлен в 5 штук.
Задача №31
Рассчитать ординаты контрольных линий (с применением контрольных карт средних арифметических значений и размахов) процесса обтачивания шейки вала диаметром 
мм, если предварительным статистическим анализом установлено, что среднее квадратическое отклонение равно 0,01 мм. Объем обработки установлен в 5 штук.
Задача №32
Рассчитать ординаты контрольных линий (с применением контрольных карт для регулирования процессов по методу медиан и крайних значений) процесса обтачивания шейки вала диаметром мм, если предварительным статистическим анализом установлено, что среднеквадратическое отклонение равно 0,01 мм, Объем выборки установлен в 5 штук. Погрешность настройки равна 0,03 мм.
Задача № 33
Рассчитать ординаты контрольных линий (с применением контрольных карт для регулирования процессов по методу медиан и крайних значений) для растачивания отверстий диаметром 130 + 0,1 мм в корпусных деталях, если предварительным статистическим анализом установлено, что среднее квадратическое отклонение равно 0,01 мм. Объем выборки установлен в
5 штук.
Задача № 34
Определить размер эталона для обработки ступенчатого вала по D = 60_о,2 мм на многорезцовом полуавтомате.
Задача №35
Определить размер эталона для обработки вала по наружной поверхности в диаметр 70 - 0,3 мм. После обработки партии валов резцом, установленным по изготовленному до предварительных размеров эталону, выявлено, что средний размер диаметра равен 70,1 мм, а среднее квадратическое отклонение 0,015 мм. Допуск на изготовление эталона принять равным 0,1 допуска детали.
Задача № 36
Определить поправку в настройку станка для обработки партии валиков по наружной цилиндрической поверхности диаметром 50 - 0,25 мм. Настройка производится по методу пробных деталей, средний размер валиков по результатам пробной обработки 5 деталей равен 49,9, среднее квадратическое отклонение - 0,02 мм, погрешности измерения и регулирования равны 0,007 мм каждая.
Задача № 37
Определить размеры эталона для обработки отверстия во втулке диаметром 60 + 0,2 мм на многорезцовом полуавтомате. После обработки партии деталей резцом, установленным по изготовленному с предварительными размерами эталону, установлено, что среднее и среднее квадратическое отклонения равны 59,9 мм и 0,012 мм соответственно. Допуск на изготовление эталона принять равным 0,1 допуска отверстия втулки.
Задача № 38
Определить поправку в настройку станка для обработки партии валиков по наружной цилиндрической поверхности диаметром 50 - 0,25 мм. Настройка производится по методу пробных деталей, средний размер валиков по результатам пробной обработки 5 деталей равен 49,9 мм, среднее квадратическое отклонение - 0,02 мм, погрешности измерения и регулирования равны 0,007 мм каждая.
Задача №39
Определить поправку в настройку станка для обработки партии валиков по наружной цилиндрической поверхности диаметром 50 - 0,25 мм. Настройка производится по методу пробных деталей, средний размер валиков по результатам пробной обработки 5 деталей равен 49,92, среднее квадратическое отклонение – 0,021 мм, погрешности измерения и регулирования равны 0,008 мм каждая.
2. Примеры решения задач
Задача №3
Генеральная средняя определяется доверительными границами
где 
Зададимся надежностью = 0,98; тогда по таблице приложения 2 [2] при k = п — 1 = 14 находим
ta = 2,62.
Поэтому
Следовательно,
т. е.
Задача № 4
По таблице приложения 3 находим для k = 15—1 = 14 и α = 0,96 qs = 0,5.
Следовательно,
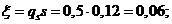
Или
Задача №16
Принимаем нулевую гипотезу, которая в данном случае будет заключаться в том, что функции распределения х и у тождественны, т. е. выборки принадлежат одной и той же генеральной совокупности. Для проверки этой нулевой гипотезы может быть использован критерий Вилькоксона, основанный на числе инверсий. Под инверсиями в данном случае понимается следующее. Наблюденные значения х и у в двух выборках располагают в общую последовательность в порядке возрастания, например, в виде
x1x2 у3 у4 у5 
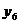x4
Если какому-либо значению х предшествует некоторый у, то говорят, что эта пара дает инверсию. Если некоторому значению хт предшествует п значений у, то это значит, что хт имеет п инверсий. Например, в нашей последовательности х1 дает две инверсии, х2 — то же две инверсии, х3 — пять инверсий и x4 — шесть инверсий. Всего инверсий в нашей последовательности будет
u = 2 + 2 + 5 + 6=15.
Расположим приведенные данные в общую последовательность в порядке возрастания в нижеприведенной таблице
| y | y | x | x | y | y | x | y | y | y | x | y | x | y | x |
| 3 | 4 | 4 | 5 | 8 | 8 | 9 | 10 | 10 | 10 | 10 | 11 | 11 | 13 | 13 |
| x | x | x | y | y | x | x | y | x | y | y | x | y | x | x |
| 13 | 14 | 14 | 15 | 16 | 17 | 17 | 18 | 19 | 20 | 20 | 20 | 21 | 23 | 27 |
| y | y | x | x | y | y | x | y | y | y | x | y | x | y | x |
| 3 | 4 | 4 | 5 | 8 | 8 | 9 | 10 | 10 | 10 | 10 | 11 | 11 | 13 | 13 |
| x | x | x | y | y | x | x | y | x | y | y | x | y | x | x |
| 13 | 14 | 14 | 15 | 16 | 17 | 17 | 18 | 19 | 20 | 20 | 20 | 21 | 23 | 27 |
Число инверсий для x будет равно
u=2+2+4+7+8+9+9+9+9+11+11+12+14+15+15=137.
При объеме выборок n > 10 и m > 10 число инверсий распределяется приблизительно по нормальному закону со средним значением
= 
= 
= 112,5;
и дисперсией
= 
(m + n + 1) = 
(15 + 15 +1) = 581,25;
Отсюда 
= 24.
Предельные значения и определяются границам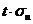и
+ 
≥ и ≥ -
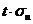
где t зависит от принятого уровня доверительной вероятности q и вычисляется по таблице 2 значений Ф(t) по формуле:
Ф(t) = 
.
Задаваясь уровнем значимости q = 0,05 и принимая во внимание, что при этом t =1,96, определим критические значения для u:
u ≥ 112,5 – 1,96·24 = 66;
u < 112,5 + 1,96·24 = 158;
Полученное значение инверсии u=137 не выходит за пределы
критической области.Поэтому принятая нулевая гипотеза не опровергается и, следовательно, нет основания считать, что станки существенно отличаются по точности.
Задача № 21
1. Показываем на эскизе поле рассеивания, по величине равное экономической точности обработки, w и центр группирования размеров. Здесь же показываем допуск размера Т = 0,08 мм и его границы на расстояниях а = 0,05 мм и в = 0,03 мм относительно центра группирования.
2. Определяем возможность получения брака. Так как поле рассеивания перекрывает поле допуска с двух сторон, то возможны оба вида брака (исправимый и неисправимый). Отношение площадей F1и F2 и общей площади, ограниченной кривой рассеивания, определяет процент брака.
3. Определяем процент брака, используя функцию Лапласа (приложение 1[5], [1, 3, 4]). Часть деталей, попадающая в брак:
FБ = F1 + F2,
в свою очередь F1 = 0,5 - Ф(а/в); F2 = 0,5 - Ф(в/d),
где d - среднее квадратическое отклонение. Воспользовавшись зависимостью w = 6d,получим d = w/6 = 0,02 мм, тогда
F1 = 0,5 – Ф(0,05/0,02) = 0,5 - Ф(2,5) = 0,5 – 0,49 = 0,01;
F2 = 0,5 – Ф(0,03/0,02) = 0,5 - Ф(1,5) = 0,5 – 0,43 = 0,07.
Таким образом, брак составит:
FБ = F1 + F2 = 0,01 + 0,07 = 0,08 (8%).
 |
Задача № 32
Для метода медиан и крайних значений для случая обработки валов имеем следующее расположение контрольных линий [2; с. 171]:
ек = Кк d = 0,5´0,01 = 0,005 мм;
ем = Км d = 1,45´0,01 = 0,015 мм;
Вк = Вт - ек = 0,2 - 0,005 = 0,195 мм;
Нк = Нт + Δн + ек = 0,1 + 0,01 + 0,005 = 0,115 мм;
Вм = Вт – ем = 0,2 - 0,015 = 0,185 мм;
Нм = Нт + Δн + ем = 0,1 + 0,01 + 0,015 = 0,125 мм.
Схема расположения контрольных линий показана на рис. Ниже.
Рис. 45
Задача № 34
Определяем предварительный размер эталона
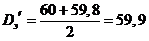
После обработки партии деталей установлено, что процесс относится к I типу точности D = 60,1 мм, s = 12 мкм.
Настроечный размер будет равен:
Dн ═ 59,8 + 3·0,012 ═ 59,84мм.
Определяем величину поправки к эталону
Окончательный размер эталона равен
D э = 59,9—0,26 = 59,64 мм.
Допуск на изготовление эталона следует принимать равным (0,1—0,15) Тэ, т. е . Тэ = 0,1-0,2= 0,02 мм. Следовательно, окончательно размер Dэ будет равен
Dэ= 59,64 ± 0,01 мм,
Задача № 38
Решение задачи осуществляем в такой последовательности:
1. Определяем погрешность настройки Δн. Для метода настройки по пробным деталям [1, 4, 6]
2. Рассчитываем настроечный размер. Для обработки валов настроечный размер Дн:
где Дmin - минимальный допустимый размер вала;
Дmin = 50 – 0,25 = 49,75 мм;
n - размер пробной партии выборки, n = 5.
Тогда
Дн = 49,75 + 0,1 + 3´0,02(1 + 1/5) = 49,85
Так как полученное после пробной обработки среднее значение размера, равное 49,9 мм, отличается от настроечного размера больше, чем погрешность настройки, необходимо ввести поправку в настройку. Ее величина равна:
П = (Дн - d)/2 = -0,025 мм.
Знак минус означает, что поправка вводится по направлению к детали.
Приложение
Таблица 1
Нормированная функция Лапласа
| t | Ф(t) | t | Ф(t) | t | Ф(t) |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0.00 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.016 0.08 0.20 0.22 0.24 0.26 0.28 0.30 0.32 0.34 0.36 0.38 0.40 0.42 0.44 0.46 0.48 0.50 0.52 0.54 0.56 0.58 0.60 0.62 0.64 0.66 0.68 0.70 0.72 2.22 2.24 2.26 2.28 2.30 2.32 2.34 2.36 2.38 2.40 2.42 2.44 2.46 | 0.0000 0.0008 0.0016 0.0024 0.0032 0.0040 0.0048 0.0557 0.0636 0.0714 0.0793 0.0871 0.0948 0.1026 0.1103 0.1179 0.1255 0.1331 0.1406 0.1480 0.1554 0.1628 0.1700 0.1772 0.1844 0.1915 0.1985 0.2054 0.2123 0.2190 0.2257 0.2324 0.2389 0.2454 0.2517 0.2580 0.2642 0.4868 0.4875 0.4881 0.4887 0.4893 0.4898 0.4904 0.4909 0.4913 0.4918 0.4922 0.4927 0.4931 | 0.74 0.76 0.78 0.80 0.82 0.84 0.86 0.88 0.90 0.92 0.94 0.96 0.98 1.00 1.02 1.04 1.06 1.08 1.10 1.12 1.14 1.16 1.18 1.20 1.22 1.24 1.26 1.28 1.30 1.32 1.34 1.36 1.38 1.40 1.42 1.44 1.46 2.48 2.50 2.52 2.54 2.56 2.58 2.60 2.62 2.64 2.66 2.68 2.70 2.74 | 0.2704 0.2764 0.2823 0.2881 0.2939 0.2995 0.3051 0.3106 0.3159 0.3212 0.3264 0.3315 0.3365 0.3412 0.3461 0.3508 0.3554 0.3599 0.3643 0.3686 0.3729 0.3770 0.3810 0.3849 0.3888 0.3925 0.3962 0.3997 0.4032 0.4066 0.4099 0.4131 0.4162 0.4192 0.4222 0.4251 0.4279 0.4934 0.4938 0.4941 0.4945 0.4948 0.4951 0.4953 0.4956 0.4959 0.4961 0.4963 0.4965 0.4969 | 1.48 1.50 1.52 1.54 1.56 1.58 1.60 1.62 1.64 1.66 1.68 1.70 1.72 1.74 1.76 1.78 1.80 1.82 1.84 1.86 1.88 1.90 1.92 1.94 1.96 1.98 2.00 2.02 2.04 2.06 2.08 2.10 2.12 2.14 2.16 2.18 2.20 2.78 2.82 2.86 2.90 3.00 3.20 3.40 3.60 3.80 4.00 4.50 5.00 | 0.4306 0.4332 0.4357 0.4382 0.4406 0.4429 0.4452 0.4474 0.4495 0.4515 0.4533 0.4554 0.4573 0.4591 0.4608 0.4625 0.4641 0.4656 0.4671 0.4688 0.4699 0.4713 0.4726 0.4738 0.4750 0.4761 0.4772 0.4783 0.4793 0.4803 0.4812 0.4821 0.4830 0.4838 0.4846 0.4854 0.4861 0.4973 0.4976 0.4979 0.4981 0.4986 0.4993 0.4996 0.4998 0.499929 0.499968 0.499997 0.499999 |
Таблица 2
Таблица значений tα для которых вероятность 
| k | Вероятность α | ||||
| 0,9 | 0,95 | 0,98 | 0,99 | 0,999 | |
| 2 | 2,02 | 4,30 | 6,97 | 9,93 | 31,60 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 | 12,94 |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 | 8,61 |
| 5 | 2,02 | 2,57 | 3,37 | 4,03 | 6,86 |
| 6 | 1,94 | 2,45 | 3,14 | 3,70 | 5,96 |
| 7 | 1,90 | 2,37 | 3,00 | 3,50 | 5,40 |
| 8 | 1,86 | 2,30 | 2,90 | 3,36 | 5,04 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 | 4,78 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 | 4,59 |
| 11 | 1,80 | 2,20 | 2,72 | 3,11 | 4,49 |
| 12 | 1,78 | 2,18 | 2,68 | 3,06 | 4,32 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 | 4,22 |
| 14 | 1,76 | 2,14 | 2,62 | 2,98 | 4,14 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 | 4,07 |
| 16 | 1,75 | 2,12 | 2,58 | 3,92 | 4,02 |
| 17 | 1,74 | 2,11 | 2,57 | 2,90 | 3,97 |
| 18 | 1,73 | 2,10 | 2,55 | 2,88 | 3,92 |
| 19 | 1,73 | 2,09 | 2,54 | 2,86 | 3,88 |
| 20 | 1,72 | 2,09 | 2,53 | 2,85 | 3,85 |
| 21 | 1,72 | 2,08 | 2,52 | 2,83 | 3,82 |
| 22 | 1,72 | 2,07 | 2,51 | 2,82 | 3,79 |
| 23 | 1,71 | 2,07 | 2,50 | 2,81 | 3,77 |
| 24 | 1,71 | 2,06 | 2,49 | 2,80 | 3,75 |
| 25 | 1,71 | 2,06 | 2,49 | 2,79 | 3,72 |
| 26 | 1,71 | 2,06 | 2,48 | 2,78 | 3,71 |
| 27 | 1,70 | 2,05 | 2,47 | 2,77 | 3,69 |
| 28 | 1,70 | 2,05 | 2,47 | 2,76 | 3,67 |
| 29 | 1,70 | 2,05 | 2,46 | 2,76 | 3,66 |
| 30 | 1,70 | 2,04 | 2,46 | 2,45 | 3,65 |
| 40 | 1,68 | 2,02 | 2,42 | 2,70 | 3,55 |
| 60 | 1,67 | 2,00 | 2,39 | 2,66 | 6,46 |
| 120 | 1,66 | 1,98 | 2,36 | 2,62 | 3,37 |
| 1,65 | 1,96 | 2,33 | 2,58 | 3,29 | |
Таблица 3
Таблица вероятностей L(q,k) ═ P(s- <0 < s+ ).
L(q,k) ═ P(0<0 < s+ ).
| k |
| |||||||||||
| 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 | |
| 6 | 0,264 | 0,388 | 0,501 | 0,599 | 0,681 | 0,791 | 0,849 | 0,886 | 0,913 | 0,948 | 0,959 | 0,987 |
| 8 | 305 | 444 | 567 | 669 | 748 | 845 | 895 | 926 | 948 | 963 | 974 | 981 |
| 10 | 340 | 491 | 620 | 722 | 797 | 882 | 925 | 961 | 968 | 979 | 986 | 991 |
| 12 | 371 | 532 | 664 | 764 | 833 | 900 | 946 | 968 | 980 | 988 | 993 | 996 |
| 14 | 399 | 567 | 701 | 798 | 862 | 929 | 960 | 978 | 988 | 993 | 996 | 998 |
| 16 | 425 | 599 | 733 | 826 | 885 | 944 | 971 | 985 | 992 | 996 | 998 | 999 |
| 18 | 448 | 627 | 760 | 849 | 903 | 955 | 980 | 990 | 996 | 998 | 999 | 999 |
| 20 | 470 | 652 | 784 | 868 | 918 | 964 | 984 | 993 | 997 | 999 | 999 | 1,000 |
| 25 | 518 | 706 | 832 | 905 | 944 | 979 | 992 | 997 | 999 | 1,000 | 1,000 | - |
| 30 | 559 | 749 | 867 | 930 | 962 | 988 | 996 | 999 | 1,000 | - | - | - |
| 35 | 597 | 787 | 893 | 944 | 969 | 990 | 997 | 999 | - | - | - | - |
| 40 | 628 | 815 | 913 | 957 | 978 | 994 | 999 | 1,000 | - | - | - | - |
| 45 | 657 | 840 | 929 | 967 | 984 | 996 | 999 | - | - | - | - | - |
| 50 | 682 | 860 | 942 | 974 | 993 | 998 | 999 | - | - | - | - | - |
| 60 | 726 | 893 | 960 | 984 | 996 | 999 | 1,000 | - | - | - | - | - |
| 70 | 762 | 917 | 972 | 990 | 998 | 1,000 | - | - | - | - | - | - |
| 80 | 792 | 935 | 980 | 994 | 999 | - | - | - | - | - | - | - |
| 90 | 818 | 949 | 986 | 996 | 999 | - | - | - | - | - | - | - |
| 100 | 840 | 959 | 990 | 997 | 1,000 | - | - | - | - | - | - | - |
| 150 | 914 | 986 | 998 | 1,000 | - | - | - | - | - | - | - | - |
| 200 | 951 | 995 | 1,000 | - | - | - | - | - | - | - | - | - |
| 250 | 972 | 998 | 1,000 | - | - | - | - | - | - | - | - | - |
| 500 | 998 | 1,000 | 1,000 | - | - | - | - | - | - | - | - | - |
| 1000 | 1,000 | 1,000 | 1,000 | - | - | - | - | - | - | - | - | - |
Таблица4
Таблица значений Zt═ 
| t | Zt | t | Zt | t | Zt |
| 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 | 0.3989 0.3980 0.3910 0.3814 0.3683 0.3521 0.3332 0.3123 0.2897 0.2661 0.2420 0.2179 0.1942 0.1714 | 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 | 0.1497 0.1295 0.1109 0.0940 0.0790 0.0656 0.0540 0.0440 0.0355 0.0289 0.0224 0.0175 0.0136 0.0104 | 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 | 0.0070 0.0060 0.0044 0.0033 0.0024 0.0017 0.0012 0.0009 0.0006 0.0004 0.0003 0.0002 |
|
|
Таблица5 Таблица вероятностей 
по распределению Стюдента
| t1 | k | ||||||||
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ∞ | |
| 0,1 | 0,922 | 0,922 | 0,922 | 0,922 | 0,922 | 0,921 | 0,921 | 0,921 | 0,9203 |
| 0,2 | 845 | 844 | 844 | 844 | 844 | 844 | 844 | 844 | 8415 |
| 0,3 | 769 | 769 | 768 | 768 | 768 | 767 | 767 | 767 | 7642 |
| 0,4 | 696 | 695 | 695 | 694 | 694 | 694 | 694 | 693 | 6892 |
| 0,5 | 625 | 625 | 624 | 624 | 623 | 623 | 623 | 623 | 6171 |
| 0,6 | 559 | 558 | 557 | 557 | 556 | 556 | 556 | 555 | 5485 |
| 0,7 | 496 | 495 | 493 | 493 | 492 | 492 | 492 | 492 | 4830 |
| 0,8 | 438 | 437 | 436 | 435 | 435 | 434 | 434 | 433 | 4237 |
| 0,9 | 384 | 383 | 382 | 381 | 331 | 380 | 379 | 379 | 3681 |
| 1,0 | 336 | 334 | 333 | 332 | 381 | 331 | 330 | 329 | 3173 |
| 1,1 | 291 | 290 | 289 | 288 | 287 | 286 | 285 | 284 | 2713 |
| 1,2 | 252 | 250 | 249 | 248 | 247 | 246 | 245 | 244 | 2301 |
| 1,3 | 216 | 215 | 213 | 212 | 211 | 210 | 209 | 208 | 1936 |
| 1,4 | 185 | 183 | 182 | 181 | 179 | 179 | 178 | 177 | 1615 |
| 1,5 | 158 | 156 | 154 | 153 | 152 | 151 | 150 | 149 | 1336 |
| 1,6 | 134 | 132 | 130 | 129 | 128 | 127 | 126 | 125 | 1096 |
| 1,7 | 113 | 111 | 110 | 108 | 107 | 106 | 105 | 105 | 0891 |
| 1,8 | 095 | 093 | 092 | 091 | 090 | 089 | 088 | 087 | 0710 |
| 1,9 | 080 | 078 | 077 | 076 | 075 | 074 | 073 | 072 | 0574 |
| 2,0 | 067 | 065 | 063 | 062 | 061 | 060 | 060 | 059 | 0455 |
| 2,1 | 056 | 054 | 053 | 052 | 051 | 050 | 049 | 049 | 0357 |
| 2,2 | 046 | 045 | 044 | 043 | 042 | 041 | 040 | 040 | 0278 |
| 2,3 | 039 | 037 | 036 | 035 | 034 | 034 | 033 | 032 | 0214 |
| 2,4 | 032 | 031 | 030 | 029 | 028 | 027 | 0,27 | 026 | 0164 |
| 2,5 | 027 | 025 | 024 | 024 | 023 | 022 | 022 | 021 | 0124 |
| 2,6 | 022 | 021 | 020 | 019 | 019 | 018 | 018 | 017 | 0093 |
| 2,7 | 018 | 017 | 016 | 016 | 015 | 015 | 014 | 014 | 0060 |
| 2,8 | 015 | 014 | 013 | 013 | 012 | 012 | 011 | 011 | 0051 |
| 2,9 | 012 | 012 | 011 | 010 | 010 | 010 | 009 | 009 | 0037 |
| 3,0 | 010 | 010 | 009 | 008 | 008 | 008 | 007 | 007 | 0027 |
| 3,1 | 008 | 008 | 007 | 007 | 006 | 006 | 006 | 005 | 0019 |
| 3,2 | 007 | 006 | 006 | 006 | 005 | 005 | 005 | 004 | 0014 |
| 3,3 | 006 | 005 | 005 | 005 | 004 | 004 | 004 | 004 | 0010 |
| 3,4 | 005 | 004 | 004 | 004 | 003 | 003 | 003 | 003 | 0007 |
| 3,5 | 004 | 004 | 003 | 003 | 003 | 003 | 002 | 002 | 0004 |
| 3,6 | 003 | 003 | 003 | 002 | 002 | 002 | 002 | 002 | 0003 |
| 3,7 | 003 | 002 | 002 | 002 | 002 | 002 | 002 | 001 | 0002 |
| 3,8 | 002 | 002 | 002 | 002 | 001 | 001 | 001 | 001 | 0001 |
| 3,9 | 002 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 0001 |
| 4,0 | 002 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 0001 |
| 4,1 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 001 | 0000 |
| 4,2 | 001 | 001 | 001 | 001 | 001 | 001 | 000 | 000 | - |
| 4,3 | 001 | 001 | 001 | 001 | 000 | 000 | - | - | - |
| 4,4 | 001 | 001 | 001 | 000 | 000 | - | - | - | - |
| 4,5 | 001 | 000 | 000 | - | - | - | - | - | - |
| 4,6 | 000 | - | - | - | - | - | - | - | - |
Таблица 6
Значения Т для доверительной вероятности Р = 0,05
| k2 | k1 для большей дисперсии | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | 
| |
| 1 | 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 |
| 3 | 10,13 | 9,55 | 9,28 | 9, 12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39" | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 |
| 12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 |
| 13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,70 | 2,64 | 2,48 | 2,29 | 2,07 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 |
| 17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 |
| 19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 |
| 21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 |
| 23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 |
| 24 | 4,26 | 3,40 | 3.01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 |
| 25 | 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 |
| 26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 |
| 27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2. 12 | 1,91 | 1,65 |
| 29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 |
| 35 | 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,52 |
| 45 | 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 |
| 50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 |
| 60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 |
| 70 | 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 |
| 80 | 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 |
| 90 | 3.95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,64 | 1,28 |
| 100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 |
| 125 | 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 |
| 150 | 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 |
| 200 | 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 |
| 300 | 3,87 | 3,03 | 2,Й | 2,41 | 2,25 | о 13 | 1,97 | 1,79 | 1,55 | 1,10 |
| 400 | 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,01. |
| 500 | 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,12 | 1,96 | 1,77 | 1,54 | 1,06 |
| 1000 | 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 |
|
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 |
|
Таблица 7
Значение 
2 в зависимости от вероятности Р
и числа k степеней свободы.
|
k
| Вероятность Р | |||||||
| 0,99 | 0,98 | 0,95 | 0,90 | 0,01 | 0,02 | 0,05 | 0,10 | |
| 4 6 9 14 19 24 29 | 0,30 0,87 2,09 4,70 7,60 10,90 14,30 | 0,43 1,13 2,53 5,4о 8,60 12,00 15,60 | 0,71 1,63 3,32 6,60 10,1 13,80 17,7 | 1,06 2,20 4,17 7,80 11,70 15,70 19,80 | 13,3 16,8 21,7 29,1 36,2 43,0 49,60 | 11,7 15,0 19,7 26,9 33,7 40,3 46,7 | 9,5 12,6 16,9 23,7 30,1 36,4 42,6 | 7,8 10,6 14,7 21,1 27,2 33,2 39,1 |
Таблица 8
Значение коэффициентов Z1 и Z2 для доверительной
Вероятности α ═ 0,95.
| n | z1 | z2 | n | z1 | z2 | n | z1 | z2 |
| 5 10 15 20 25 | 0,599 0,688 0,732 0,760 0,781 | 2,875 1,826 1,577 1,46 1,391 | 30 40 50 60 70 | 0,796 0,819 0,835 0,848 0,875 | 1,344 1,284 1,246 1,220 1,200 | 80 90 100 200 - | 0,865 0,872 0,878 0,911 - | 1,184 1,172 1,162 1,109 - |
|
| Р( )
| 
| Р( )
|
| Р( )
|
| Р( )
|
| 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 | 1,000 0,9997 0,9972 0,9874 0,9639 0,9228 0,8643 0,7920 | 0,70 0,75 0,80 0,85 0,90 0,95 1,00 1,10 | 0,7112 0,6272 0,5441 0,4653 0,3927 0,3275 0,2700 0.1777 | 1,20 1,30 1,40 1,50 1,60 1,70 1,80 | 0,1122 0,0681 0,0397 0,0222 0,0120 0,0062 0,0032 | 1,90 2,00 2,10 2,20 2,30 2,40 2,50 | 0,0015 0,0007 0,0003 0,0001 0,0001 0,0000 0,0000 |
Таблица9
Критические значения G при 5%-ном уровне значимости.
| m - число выбо- рок | n - 1 (n – объем выборки) | |||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 3 4 5 6 7 8 9 10 12 15 20 | 0,9975 08709 0,7669 0,6838 0,6161 0,5612 0,5157 0,4775 0,4450 0,3924 0,3346 0,2705 | 0,9393 0,7977 0,6841 0,5981 0,5321 0,4800 0,4377 0,4027 0,3733 0,3264 0,2759 0,2205 | 0,9056 0,7457 0,6278 0,5441 0,4803 0,4307 0,3910 0,3584 0,3311 0,2880 0,2419 0,1921 | 0,8772 0,7071 0,5895 0,5065 0,4447 0,3974 0,3595 0,3286 0,3029 0,2624 0,2195 0,1735 | 0,8534 0,6771 0,5598 0,4763 0,4184 0,3726 0,3362 0,3067 0,2823 0,2439 0,2034 0,1602 | 0,8332 0,6530 0,5365 0,4564 0,3980 0,3535 0,3185 0,2901 0,2660 0,2299 0,1911 0,1501 | 0,8130 0,6333 0,5175 0,4387 0,3817 0,3384 0,3043 0,2768 0,2541 0,2187 0,1815 0,1422 | 0,8010 0,6167 0,5017 0,4241 0,3682 0,3259 0,2926 0,2659 0,2439 0,2098 0,1736 0,1357 |
Таблица 10
Значения вероятностейР( ) для различных
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Маталин А.А. Технология машиностроения. М.: Машиностроение, 1985. 512 с.
2. Солонин И.С. Математическая статистика в технологии машиностроения. М.: Машиностроение, 1972. 215 с.
Дата добавления: 2018-02-15; просмотров: 1257; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!