Дифференциальные уравнения второго порядка.
Простейшие дифференциальные уравнения первого порядка вида . Запишем несколько примеров таких ДУ . Дифференциальные уравнения можно разрешить относительно производной, произведя деление обеих частей равенства на f(x). В этом случае приходим к уравнению , которое будет эквивалентно исходному при f(x) ≠ 0. Примерами таких ОДУ являются . Если существуют значения аргумента x, при которых функции f(x) и g(x)одновременно обращаются в ноль, то появляются дополнительные решения. Дополнительными решениями уравнения при данных xявляются любые функции, определенные для этих значений аргумента. В качестве примеров таких дифференциальных уравнений можно привести . В статье простейшие дифференциальные уравнения первого порядка. Вы можете ознакомиться с подробной теорией и посмотреть примеры решения таких ОДУ. · Дифференциальные уравнения с разделяющимися переменными вида или . Дифференциальные уравнения называют уравнениями с разделенными переменными. Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него. Общее решение дифференциальных уравнений с разделенными переменными можно найти, проинтегрировав обе части равенства: ∫ f(y)dy = ∫ f(x)dx. В качестве примеров ОДУ с разделенными переменными приведем . Дифференциальные уравнения с разделяющимися переменными приводятся к ОДУ с разделенными переменными делением обеих частей уравнения на произведение f2(y) ⋅ g1(x). То есть, получим . Такое преобразование будет эквивалентным, если одновременно f2(y) ≠ 0 и g1(x) ≠ 0. Иначе могут потеряться некоторые решения. Примерами ОДУ с разделяющимися переменными являются . Некоторые дифференциальные уравнения можно свести к уравнениям с разделяющимися переменными с помощью замены переменных. Дифференциальные уравнения приводятся к ОДУ с разделяющимися переменными подстановкой z = ax+by. К примеру, уравнение с помощью подстановки z = 2x+3y приобретает вид . ОДУ или преобразуются к уравнениям с разделяющимися переменными с помощью замен или . Например, дифференциальное уравнение после замены принимает вид . Некоторые дифференциальные уравнения следует немного преобразовать, чтобы можно провести замену. К примеру, достаточно разделить на x2 или y2числитель и знаменатель правой части дифференциального уравнения , чтобы оно соответствовало случаям или соответственно. Дифференциальные уравнения преобразуются к только что рассмотренным ОДУ или , если ввести новые переменные , где - решение системы линейных уравнений и провести некоторые преобразования. Например, дифференциальное уравнение после введения новых переменных преобразуется к виду . Проводим деление на u числителя и знаменателя правой части полученного уравнения и принимаем . В результате приходим к уравнению с разделяющимися переменными . В разделе дифференциальные уравнения с разделяющимися переменнымиподробно разобрана теория и приведены подробные решения аналогичных примеров. · Линейные неоднородные дифференциальные уравнения первого порядка . В качестве примеров линейных неоднородных дифференциальных уравнений первого порядка можно привести . Для решения ЛНДУ используют метод вариации произвольной постоянной. Также существует метод, основанный на представлении искомой функции y в виде произведения: y(x) = u(x)v(x). В статье линейные неоднородные дифференциальные уравнения первого порядка подробно изложены методы интегрирования таких ЛНДУ и приведены подробные решения примеров и задач. · Дифференциальное уравнение Бернулли . Примерами дифференциальных уравнений Бернулли являются, например, . Дифференциальное уравнение Бернулли сводится к линейному дифференциальному уравнению первого порядка подстановкой . Можно также пользоваться методом, основанным на представлении функции yкак y(x) = u(x)v(x). В разделе дифференциальное уравнение Бернулли подробно расписаны методы нахождения решений и разобраны решения примеров и задач. · Уравнения в полных дифференциалах . Если для любых значений x и y выполняется , то этого условия необходимо и достаточно, чтобы выражение P(x, y)dx+Q(x, y)dyпредставляло собой полный дифференциал некоторой функции U(x, y) = 0, то есть, dU(x, y) = P(x, y)dx + Q(x, y)dy. Таким образом, задача сводится к восстановлению функции U(x, y) = 0 по ее полному дифференциалу. К примеру, левая часть дифференциального уравнения представляет собой полный дифференциал функции . Подробное описание теории и решение примеров изложены в разделе уравнения в полных дифференциалах. К началу страницы
|
|
|
|
|
|
|
|
|
Дифференциальные уравнения второго порядка.
· Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами 
.
ЛОДУ с постоянными коэффициентами является очень распространенным видом дифференциальных уравнений. Их решение не представляет особой сложности. Сначала отыскиваются корни характеристического уравнения 
. При различных p и q возможны три случая: корни характеристического уравнения могут быть действительными и различающимися 
, действительными и совпадающими 
или комплексно сопряженными 
. В зависимости от значений корней характеристического уравнения, записывается общее решение дифференциального уравнения как 
, или 
, или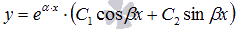 
соответственно.
|
|
|
Для примера рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами 
. Корнями его характеристического уравнения 
являются k 1 = -3 и k 2 = 0. Корни действительные и различные, следовательно, общее решение ЛОДУ с постоянными коэффициентами имеет вид
Подробное описание теории и разобранные решения примеров и задач смотрите в разделе линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
· Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 
.
Общее решение ЛНДУ второго порядка с постоянными коэффициентами yищется в виде суммы 
общего решения соответствующего ЛОДУ 
и частного решения 
исходного неоднородного уравнения, то есть, 
. Нахождению общего решения однородного дифференциального уравнения с постоянными коэффициентами , посвящен предыдущий пункт. А частное решение определяется либо методом неопределенных коэффициентов при определенном виде функции f(x), стоящей в правой части исходного уравнения, либо методом вариации произвольных постоянных.
В качестве примеров ЛНДУ второго порядка с постоянными коэффициентами приведем
Разобраться в теории и ознакомиться с подробными решениями примеров мы Вам предлагаем на странице линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
· Линейные однородные дифференциальные уравнения (ЛОДУ) 
и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка 
.
Частным случаем дифференциальных уравнений этого вида являются ЛОДУ и ЛНДУ с постоянными коэффициентами.
Общее решение ЛОДУ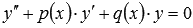 
на некотором отрезке [a; b]представляется линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, 
.
Главная сложность заключается именно в нахождении линейно независимых частных решений дифференциального уравнения этого типа. Обычно, частные решения выбираются из следующих систем линейно независимых функций:
Однако, далеко не всегда частные решения представляются в таком виде.
Примером ЛОДУ является 
.
Общее решение ЛНДУ 
ищется в виде , где - общее решение соответствующего ЛОДУ, а - частное решение исходного дифференциального уравнения. О нахождении мы только что говорили, а можно определить, пользуясь методом вариации произвольных постоянных.
В качестве примера ЛНДУ можно привести 
.
Теорию и решение примеров смотрите в разделе линейные дифференциальные уравнения второго порядка.
К началу страницы
Дата добавления: 2018-02-15; просмотров: 387; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!