Тема 3. СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИ
ЗАДАЧИ
Задача 1. Имеются следующие данные по двум цехам предприятия за два периода:
| I квартал | II квартал | |||
| Цеха | Число рабочих | Заработная плата 1 рабочего, тыс.р. | Фонд заработной платы, тыс.р. | Заработная плата 1 рабочего, тыс. р. |
| N 1 | 100 | 640 | 66640 | 680 |
| N 2 | 90 | 720 | 63750 | 750 |
Определить среднюю заработную плату одного рабочего на предприятии: а) за I квартал; б) за II квартал.
Задача 2. Определить по нижеследующим данным среднюю рентабельность продукции акционерного общества за базисный и за отчетный год:
| Базисный год | Отчетный год | |||
| АО | Рентабель-ность % | Полная себес-тоимость про- дукции млн.р. | Рентабель-ность % | Прибыль млн.р. |
| предприятие 1 | 20 | 890 | 19 | 165 |
| предприятие 2 | 18 | 750 | 21 | 150 |
Задача 3. Известны следующие данные по трем автотранспортным предприятиям:
| АТП | Фактический объем перевозок, млн. тонн. | Процент выполнения плана перевозок | Удельный вес городских перевозок (%). |
| N 1 | 250 | 105 | 60 |
| N2 | 400 | 98 | 50 |
| N3 | 640 | 100 | 72 |
Определить: 1) средний процент выполнения плана перевозок по трем АТП; 2) среднюю долю городских перевозок в целом по трем АТП.
Задача 4. Имеются данные о выполнении плана объема продукции по двум цехам предприятия за два квартала.
|
|
|
| I квартал | II квартал | |||
| Цеха | плановое задание по выпуску продукции, млн.р. | % выполнения плана выпуска продукции | фактический выпуск продукции, млн.руб. | % выполнения плана выпуска продукции |
| N 1 | 740 | 105 | 906 | 110 |
| N 2 | 810 | 101 | 885 | 104 |
Определить средний процент выполнения плана по выпуску продукции за I квартал по предприятию в целом и за II квартал.
Задача 5. Известны следующие данные о распределении рабочих предприятия по стажу работы (лет).
| Стаж работы | Число рабочих |
| до 5 | 15 |
| 5 - 10 | 25 |
| 10 - 15 | 12 |
| 15 - 20 | 28 |
| 20 и более | 20 |
Определить средний стаж работы одного рабочего обычным способом и способом моментов.
Задача 6. По условию предыдущей задачи найти моду и медиану стажа работы рабочих.
Задача 7. Распределение рабочих по уровню выработки характеризуется следующими данными:
| Выработка 1 рабочего в тыс. р. | Число рабочих |
| 400 - 600 | 21 |
| 600 - 700 | 50 |
| 700 - 800 | 75 |
| 800 и выше | 49 |
Вычислить среднюю выработку продукции одного рабочего и модальную выработку.
|
|
|
Задача 8. Дано распределение рабочих предприятия по возрасту (лет).
| Возраст рабочих | Количество рабочих, в том числе: всего цех 1 цех 2 | ||
| до 20 | 5 | 2 | 3 |
| 20 - 25 | 13 | 7 | 6 |
| 25 - 30 | 18 | 11 | 7 |
| 30 - 35 | 52 | 22 | 30 |
| 35 - 40 | 23 | 15 | 8 |
| 40 и старше | 9 | 4 | 5 |
Определить средний возраст одного рабочего, используя способ моментов, а также медиану возраста одного рабочего по предприятию.
Задача 9. Вычислить по данным распределения деталей по длительности их обработки следующие показатели: среднюю длительность обработки одной детали, моду и медиану.
| Затраты времени на обработку одной детали мин. | Число деталей |
| 40 -44 | 7 |
| 44 -48 | 15 |
| 48 -52 | 22 |
| 52 -56 | 14 |
| 56 -60 | 12 |
Задача 10. По данным условия задачи N9 определить следующие показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение и коэффициент вариации.
Задача 11. По условию. задачи N8 сопоставить степень вариации возраста рабочих цеха N1 и N2, сделать вывод.
Задача 12 .По данным задачи N7 рассчитать дисперсию обычным способом и способом моментов, а также дать оценку степени вариации выработки одного рабочего на предприятии.
|
|
|
Задача 13. На основе исходных данных к задаче 5 рассчитать следующие показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Задача 14. Известны следующие данные об урожайности озимой пшеницы по двум районам области:
| Урожайность в ц с 1 га | Посевная площадь в га I район II район | |
| до 18 | 400 | 250 |
| 18 - 20 | 180 | 305 |
| 20 - 22 | 290 | 115 |
| 22 и выше | 230 | 100 |
Сравнить степень вариации урожайности по двум районам области. Сделать вывод.
Задача 15. Трудоемкость изготовления одной детали на станках-автоматах 1,2 часа, на обычных станках 2,5 часа. На станках-автоматах изготовлено 50 деталей, на обычных станках - 20. Определить дисперсию трудоемкости деталей упрощенным методом.
Задача 16. Урожайность яровой пшеницы на 500 га - 25 ц с 1 га, на 600 га - 30 ц с 1 га. Рассчитать дисперсию урожайности упрощенным методом.
Задача 17. Определить дисперсию и среднее квадратическое отклонение признака, если известно, что в партии 10000 электроламп, 30 штук оказались бракованными.
|
|
|
Задача 18. Выпуск всей продукции на предприятии составил 610 млн. р., в том числе 1 сорта 396,5 млн.р. Вычислить дисперсию удельного веса продукции 1 сорта.
Задача 19. Удельный вес отличников в общей численности студентов вуза составляет 12%. Найти дисперсию доли студентов- отличников.
Задача 20. Урожайность картофеля на отдельных участках поля характеризуется следующими данными:
| Урожайность | Участки га | ||
| в ц с га | всего | в том числе | |
| неудобренные | удобренные | ||
| до 100 | 28 | 24 | 4 |
| 100 -110 | 48 | 25 | 23 |
| 110 - 120 | 20 | 10 | 10 |
| 120 и более | 4 | 1 | 3 |
| Итого | 100 | 60 | 40 |
Рассчитать следующие показатели: 1) среднюю урожайность картофеля на всем массиве, на неудобренных и удобренных участках, 2) дисперсию общую, среднюю, внутригрупповую и межгрупповую.
Проверить правило сложения дисперсий.
Задача 21. Средний балл успеваемости у студентов очной формы обучения - 4, заочной - 3. Доля студентов - очников - 75%, а заочников 25% в общей численности студентов вуза. Средняя групповая дисперсия успеваемости студентов 0,18. Определить общую дисперсию успеваемости студентов.
Задача 22. Известны данные о заработной плате рабочих автотранспортного предприятия:
| Профессия | Месячная зарплата 1 работника в тыс. р. | |||||||
| водители | 905 | 948 | 1010 | 1040 | 980 | 991 | 988 | 952 |
| ремонтные рабочие | 793 | 756 | 925 | 915 | 930 | 900 | 799 | 818 |
На основе приведенных данных проверить правило сложения дисперсий.
Задача 23. По условию задачи 14 рассчитать межгрупповую, общую дисперсии, а на их основе среднюю из групповых.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Задача 2. Основой расчета средней величины является экономическое содержание показателя (исходное соотношение).
Средняя прибыль
рентабельность = –––––––––––––––––––––––––––––
продукции полная себестоимость продукции
В том случае, если знаменатель исходного соотношения известен для расчета средней величины применяют формулу средней арифметической взвешенной. если же знаменатель соотношения неизвестен - расчет производится по формуле средней гармонической взвешенной.
Для расчета средней рентабельности продукции предприятия в базисном году применяем формулу средней арифметической взвешенной:
S xf 0, 20 * 890 +0,18 * 750
Х = ------ = ------------------- = 0,191 или 19,1%
S f 890 + 750
За отчетный год среднюю рентабельность продукции определяем по формуле средней гармонической взвешенной:
S xf 165 + 150
Х = ------------ = ------------------------------- = 0,199 или 19,9 %
S (xf / x) (165 / 0,19) + (150 / 0,21)
Задача 5. среднее значение признака из интегрального ряда можно определить двумя способами:
S xf
1) по средней арифметической взвешенной: x = ------------
S f
В этой формуле за величину x принимается средняя интервала в каждой группе:
2) по способу моментов:
[S ( X - A) / i] * f
Х = А +m1 * i , где m1 = ----------------------
S f
А - постоянная величина, за которую принимается варианта (середина интервала) находящаяся в центре ряда.
i - величина интервала.
Способы расчета представим в следующей таблице.
| стаж работы (лет) | число рабочих | середина интервала Х | Х-А=Х-12,5 | х-а i | [( x-a)/ i ]*f |
| до 5 | 15 | (0+5)/2=2,5 | -10 | -2 | -30 |
| 5 -10 | 25 | (5+10)/2=7,5 | -5 | -1 | -25 |
| 10 - 15 | 12 | (10+15)/2=12,5 | 0 | 0 | 0 |
| 15 - 20 | 28 | (15+20)/2=17,5 | +5 | +1 | +28 |
| 20 и более | 20 | (20+25)/2=22,5 | +10 | +2 | +40 |
| Итого | 100 | +13 |
I способ расчета:
Х = S xf = 2,5*15+7,5*25+12,5*12+17,5*28+22,5*20 = 1315 = 13,2 года
S f 100 100
II способ расчета,
подставив данные таблицы в формулы, получим:
x = 12,2 + (13 / 100) * = 13,2 года
Оба способа расчета дали одинаковый результат.
В интервальных рядах с с равными интервалами определяют моду и медиану.
Модальный интервал устанавливают по наибольшей частоте. В нашей задаче наибольшая частота - 28, следовательно, мода находится в интервале от 15 - 20. Затем рассчитывают значение моды по формуле:
fмод - f предмод
Mо = o + i * ------------------------------------------
( fмод - f предмод ) +( f мод - f последмод )
где Хо - нижняя граница модального интервала,
fпослемод - частота интервала, следующего за модальным;
fпредмод - частота интервала, предшествующего модальному.
Подставляем числовые значения в формулу:
Мо =( 15 +5 )* (28 - 12) / [ (28-12)+(28-20) ] = 15 +5 * 0,667 = 18,3 года
Вывод: наиболее часто встречаются рабочие со стажем работы 18,3 года.
Медианный интервал устанавливают по накопленным частотам.
Построим ряд накопленных частот:
| Стаж работы (лет) | Число рабочих f | Накопленные частоты Sn |
| до 5 | 15 | 15 |
| 5 - 10 | 25 | 15 + 25 = 40 |
| 10 - 15 | 12 | 40 + 12 = 52 |
| 15 - 20 | 28 | 52 + 28 = 80 |
| 20 и более | 20 | 80 + 20 = 100 |
Итого: 100
Медиана должна находиться в том интервале, где первая накопленная частота равна половине всей совокупности или больше половины ее. В нашей задаче половина совокупности -50 (100/2), а первая накопленная частота, которая больше половины совокупности - это 52, значит медицина находится в интервале 10 - 15.
Расчет непосредственно медианы производится по формуле:
S f/2 - S n - 1
М е = Хо + i f me
где: Хо - нижняя граница медианного интервала;
i - величина интервала,
S f - сумма всех частот,
Sn-1 - сумма накопленных частот, предшествующих медианному интервалу,
fme - частота медианного интервала.
Ме = (10 + 5 ) * (100 / 2 - 40) / 12 = 14,2 года.
Таким образом, половина рабочих имеет стаж работы до 14,2 года, а другая свыше 14,2 года.
По условию задачи N5 рассчитаем показатели вариации.
1. Размах вариации как разность экстремальных значений признака:
R = Xmax - Xmin
R = 22,5 - 2,5 = 20 лет
2. Среднее линейное отклонение как средняя арифметическая взвешенная из абсолютных отклонений индивидуальных значений от средней величины:
S / x-x/f
L = --------------
S f
L=[/12,5-13,2/*15+/7,5-13,2/*25+/12,15-13,2/*12+/17,5-13,2/*28+/22,5--13,2/*20] / 100 = 616 / 100 = 6,16
3.Дисперсия - это средний квадрат отклонений индивидуальных значений от средней величины. Дисперсию можно рассчитать несколькими способами.
По формуле:
S ( x - x)2 f
G2 = S f
G2=[(2,5-13,5)2*15+(7,5-13,5)2*25+(12,5-13,5)2*12+(17,5-13,5)2*28+(22,5-13,5)2*20] / 100 = 4783 / 100 = 47,83
Второй способ расчета дисперсии по способу моментов основан на математических свойствах дисперсии и производится по формуле:
G2 = (m2 - m12)*i2
где i - величина интервала.
S[(x-a) / i]*f S[(x-a) / i]2*f
m1 = S f , m2 = S f
| стаж работы (лет) | число рабочих f | середина интервала х | х - а | (x - a) / i | [(x-a)/i]*f | [(x-a)/i]2 | [(x-a)/i]2*f |
| до 5 | 15 | 2,5 | -10 | -2 | -30 | 4 | 60 |
| 5 - 10 | 25 | 7,5 | -5 | -1 | -25 | 1 | 25 |
| 10 - 15 | 12 | 12,5 | 0 | 0 | 0 | 0 | 0 |
| 15 - 20 | 28 | 17,5 | +5 | +1 | +28 | 1 | 28 |
| 20 и более | 20 | 22,5 | +10 | +2 | +40 | 4 | 80 |
| Итого | 100 | +13 | 193 |
Исчислим моменты первого и второго порядков (m1 и m2):
S[(x-a) / i]*f
m1 = S f = 13 / 100 = 0,13
S[(x-a) / i]2*f
m2 = S f = 193 / 100 = 1,93
i - величина интервала равна 5, тогда
G2 = (m2 - m12)*i2
G2 = (1,93 - 0,132)*52 = (1,93-0,0169)*25 = 47,83
4. Среднее квадратическое отклонение - это корень квадратный из дисперсии:
G = ± 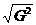
_
G = ± 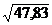 = ± 6,9 года
= ± 6,9 года
Коэффициент вариации - относительный показатель колеблемости, равный процентному отношению среднего квадратического отклонения к средней величине:
V = ± 
V = ± 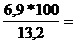 52,3%
52,3%
Коэффициент вариации применяется для сравнения степени вариации признака по различным совокупностям (см. задачи N11 и N 14).
Задача 16. Исчислим дисперсию упрощенным способом:
__ _
G2 = х2 - х2
 х2 =
х2 = 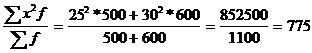
 х -2
х -2 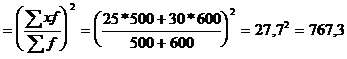
G2 = 775 - 767,3 = 7,7
Задача 18. Дисперсия альтернативного признака (или дисперсия доли) исчисляется по формуле:
G2 = p + q
где р - доля единиц, обладающих данным признаком.
q - доля единиц, не обладающая этим признаком.
Поэтому р + q = 1 q = 1 - р
В нашей задаче доля продукции 1 сорта равна : р = 396,5 / 610 = 0,65 или 65% . Следовательно, 35% продукции не относятся к 1 сорту, т.е. не обладают данным признаком. (q = 1 - 0,65 = 0,35) Следовательно, дисперсия удельного веса продукции 1 сорта :
G2 = 0,65 * 0,35 = 0,23
Задача 20.
1. Рассчитаем среднюю урожайность картофеля по формуле:
 |
х 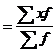
на всем массиве:
__
Хобщ = (95*28+105*48+115*20+125*4) / 100 = 105 ц с 1 га
на удобренных участках:
__
Хгр = (95*4+105*23+115*10+125*3) / 40 = 108 ц с 1 га
на неудобренных участках:
__
Хгр = (95*24+105*25+115*10+125*1) / 40 = 108 ц с 1 га
2. Исчислим дисперсии по каждой группе участков по формуле:
_
G2ГР = S (xi - xгр)2 f
S f
по неудобренным участкам:
G2ГР = [(95-103)2*24+(105-103)2*25+(115-103)2*10+(125-103)2*1] / 60 = 59,3
по удобренным участкам:
G2ГР = [(95-108)2*4+(105-108)2*23+(115-108)2*10+(125-103)2*3] / 40 = 56
Из рассчитанных групповых дисперсий определим среднюю:
____
G2ГР = S G2гр f = (59,3*60+56*40) / (60+40) = 58
S f
3. Межгрупповая дисперсия рассчитывается по формуле:
G2 межгр = [S ( xгр - х общ)2 f ] / S f
G2 межгр = [ (103-105)2*60+(108-105)2*40] / (60+40) = 6
4. Определим общую дисперсию:
G2 общ =[S ( xi - х общ)2 f ] /S f
G2 общ =[(95-105)2*28+(105-105)2*48+(115-105)2*20+(125-105)2*4] / 100 = 64
Правило сложения дисперсий:
____
G2 общ = G2ГР + G2межгр
64 = 58 + 6
Межгрупповая дисперсия показывает вариацию результативного признака под влиянием признака-фактора. Так, в нашей задаче межгрупповая дисперсия характеризует колеблемость урожайности в зависимости от внесения удобрений.
Средняя из групповых дисперсий говорит о степени вариации результативного признака под влиянием всех прочих факторов, кроме признака фактора. А общая дисперсия отражает влияние всей совокупности факторов на колеблемость результативного признака.
Тема 4. РЯДЫ ДИНАМИКИ
ЗАДАЧИ
Задача 1. Рассчитать следующие показатели анализа рядов динамики: цепные и базисные абсолютные приросты, коэффициенты, темпы роста и прироста, абсолютное значение одного процента прироста.
| годы | 1992 | 1993 | 1994 | 1995 | 1996 |
| выплавка стали (тыс. т) | 1160 | 1210 | 1260 | 1310 | 1360 |
Задача 2. Динамика численности населения Российской Федерации за 1990 - 1993 г.г. характеризуется следующими данными (на конец года млн. чел.).
| 1990 | 1991 | 1992 | 1993 | |
| всего населения в том числе: | 148,2 | 148,3 | 148,3 | 148 |
| моложе трудоспособного возраста | 36,0 | 35,7 | 35,2 | 34,5 |
| в трудоспособном возрасте | 84 | 83,9 | 83,7 | 83,9 |
| старше трудоспособного возраста | 28,2 | 28,7 | 29,4 | 29,6 |
По каждой возрастной группе определите: 1) цепные и базисные абсолютные приросты 2) цепные и базисные коэффициенты роста, темпы роста и темпы прироста.
Задача 3. Известны данные о среднегодовой численности занятых в экономике на предприятиях негосударственных форм собственности.
| годы | 1990 | 1991 | 1992 | 1993 |
| млн.чел. | 13,1 | 18,1 | 23,8 | 29,5 |
Определить цепные и базисные абсолютные приросты, коэффициенты, темпы роста и прироста, а также абсолютное содержание одного процента прироста.
Задача 4. Численность населения области на 1.1.1992 - 420 тыс. человек, на 1.1.1996 г. - 432 тыс. человек. Определить средний коэффициент роста, темп роста и темп прироста населения за 1992 - 1996 годы и спрогнозировать численность населения области на 1.1.1998 года.
Задача 5. Известны остатки товарных запасов на складе предприятия (в млн. руб.).
| 1.1.1996 | 1.2.1996 | 1.3.1996 | 1.4.1996 |
| 480 | 520 | 390 | 610 |
Определить: 1) среднеквартальный остаток товарных запасов на складе предприятия , 2) средний темп роста и прироста товарных запасов за I квартал.
Задача 6. По автотранспортному предприятию имеются следующие данные об объеме перевозок в среднем за три года в тыс. т
| месяцы | тыс.тн. | месяцы | тыс.тн. |
| январь | 2408 | июль | 2822 |
| февраль | 2431 | август | 2783 |
| март | 2592 | сентябрь | 2642 |
| апрель | 2642 | октябрь | 2501 |
| май | 2672 | ноябрь | 2307 |
| июнь | 2703 | декабрь | 2321 |
На основании приведенных данных рассчитать индексы сезонности и измерить степень сезонных колебаний.
Задача 7. Численность рабочих на предприятии характеризовалась следующими данными: за январь - 250 человек, за февраль - 252, за март - 260, на 1 апреля 255, на 1 мая 248, на 1 июня 252, на 1 июля - 254. Определить среднюю численность рабочих 1) I квартал; 2) II квартал; 3) полугодие в целом.
Задача 8. Известны следующие данные об урожайности пшеницы за 12 лет в ц с 1га.
| годы | ц | годы | ц | годы | ц |
| 1980 | 18 | 1984 | 20,1 | 1988 | 20,4 |
| 1981 | 19,5 | 1985 | 19,4 | 1989 | 19,6 |
| 1982 | 19,8 | 1986 | 17,8 | 1990 | 20,2 |
| 1983 | 17,5 | 1987 | 18,8 | 1991 | 21,5 |
Выявить основную тенденцию динамики урожайности, используя следующие методы; 1) укрупнение интервалов; 2) скользящей средней; 3) выравнивание по прямой.
Задача 9. Среднемесячный выпуск продукции за 1991 - 1993 годы по месяцам составлял млн. р.:
| месяцы | млн.р. | месяцы | млн.р. | месяцы | млн.р. |
| январь | 380,5 | май | 430.2 | сентябрь | 480.8 |
| февраль | 408.6 | июнь | 527.7 | октябрь | 574.1 |
| март | 167.2 | июль | 485.9 | ноябрь | 400.0 |
| апрель | 430,2 | август | 535.4 | декабрь | 380.3 |
Рассчитать индексы сезонности и измерить степень сезонной неравномерности выпуска продукции.
Задача 10. Имеются сведения об остатках оборотных средств на предприятии в млн.р.
| 1.10.1990 | 1.10.1991 | 1.10.1992 | 1.1.1991 | 1.1.1992 | 1.1.1993 |
| 800 | 840 | 850 | 886 | 945 | 980 |
Сомкнуть ряд динамики и рассчитать средний темп роста и средний абсолютный прирост.
Задача 11. По условию задачи 10 рассчитать средний уровень ряда, цепные и базисные темпы роста и прироста.
Задача 12. Имеются данные о товарообороте района по месяцам года в млрд. р. : 1 -7,4; 2 - 7,9; 3 - 8,7; 4 - 8,2; 5 - 7,9; 6 - 8,2; 7 - 8,8; 8 - 8,7; 9 - 8,7; 10 - 8,1; 11 - 8,3; 12 - 9. Произвести сглаживание методом скользящей средней и выравнивание ряда по прямой.
Задача 13. Абсолютное содержание одного процента прироста составило в 1991г. - 4,2 тыс. руб., темп прироста выработки в 1991г. по сравнению с 1990 г составил 8%, базисный коэффициент роста в 1992 г. составил 1,12, а абсолютный цепной прирост в 1993г. составил 82,тыс.р. Построить ряд динамики выработки продукции за 1990 - 1993 годы.
 Задача 14. Динамика производительности труда за 1986 - 1996г. характеризуется уравнением прямой:
Задача 14. Динамика производительности труда за 1986 - 1996г. характеризуется уравнением прямой:
Yt = 4155 +32 t.
Спрогнозировать уровень производительности труда на 1995 год.
Задача 15. Имеются данные об урожайности ячменя за 1988 - 1996гг. (ц).
| 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
| 10 | 10,7 | 12 | 10,3 | 12,9 | 16,3 | 15,6 | 17,8 | 18 |
Выявить основную тенденцию урожайности за 1988 - 1996 гг.: 1) методом сглаживания ряда с помощью скользящей средней; 2) методом аналитического выравнивания по уравнению прямой.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Задача 1. Показателями анализа ряда динамики являются:
1) абсолютный прирост (D) как разность двух сравнительных уровней;
цепной D = Yn - Yn-1
базисный D = Yn - Y1
где Yn - каждый последующий уровень ряда динамики
Yn-1 - предшествующий уровень
Y1 - начальный уровень ряда
2) коэффициенты роста (К) - это отношение уровня последующего ряда к уровню предыдущего или начального.
коэффициент цепной K = 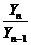
коэффициент базисный K = 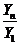
3) темп роста - это коэффициент роста, выраженный в процентах.
Т = К * 100
4) темп прироста (t) есть отношение абсолютного прироста к предыдущему или начальному уровню, т.е.
t  или t
или t 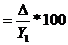
Темп прироста может быть также вычислен путем вычитания из темпа роста 100%, т.е. t = T - 100%
5) Абсолютное содержание одного процента прироста определяется делением абсолютного прироста на соответствующий темп прироста:
а 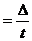
Этот показатель можно определить также и делением предшествующего уровня на 100.
Рассчитанные аналитические показатели изложили в табличной форме:
| Показатели | 1992 | 1993 | 1994 | 1995 | 1996 |
| Выплавлено стали (тыс. т) | 1160 | 1210 | 1260 | 1310 | 1360 |
| Абсолютные приросты (тыс.т) цепные (по сравн. с пред. год.) | - | +50 | +50 | +50 | +50 |
| базисные (по сравн. с 1990) | - | +50 | +100 | +150 | +200 |
| Коэффициенты роста цепные (по сравн. с пред. год.) | 1 | 1,043 | 1,041 | 1,039 | 1,038 |
| базисные (к 1990г.) | 1 | 1,043 | 1,086 | 1,129 | 1,172 |
| Темпы роста (в %) цепные | 100 | 104,3 | 104,1 | 103,9 | 103,8 |
| базисные | 100 | 104,3 | 108,6 | 112,9 | 117,2 |
| Темпы прироста (в %) цепные | - | +4,3 | +4,1 | +3,9 | +3,8 |
| базисные | - | +4,3 | +8,6 | +12,9 | +17,2 |
| Абсолютное содержание одного процента прироста (т. т) | - | 1,16 | 1,21 | 1,26 | 1,31 |
Средний абсолютный прирост:
D 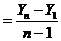 D
D 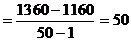 тыс.т
тыс.т
Средний коэффициент определяется по формуле средней геометрической:

 К =
К = 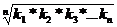 или К =
или К = 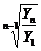
 К =
К = 
 К =
К = 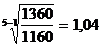
Средний темп роста:
__ __ __
Т = К * 100 Т = 1,04 * 100 = 104 %
Средний темп прироста:
_ __ _
t = T - 100 t = 104 - 100 = 4 %.
Задача 7. Средний уровень периодического ряда динамики определяется по формуле средней арифметической простой:

 У
У 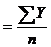 У
У 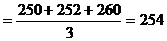 чел.
чел.
Средний уровень моментного ряда динамики рассчитывается по средней хронологической:
__
У = (У1/2 + У2 + У3 + . . . Уn/2 ) / n - 1
__
У = (255/2 + 248 + 252 + 254/2) / (4 - 1) = 251,5
Задача 6. Для анализа рядов внутригодовой динамики рассчитываются индексы сезонности по формуле:
__ __ __
ie = Умес / Угод где Умес - средний месячный уровень за 3 года,
__
Угод - среднегодовой уровень за 3 года.
Среднегодовой уровень за три года:
(2408+2431+2592+2642+2672+2703+2822+2783+2642+2501+2307+2321) / 12 = = 30824 / 12 = 2568,7
Тогда индекс сезонности:
за январь ie = 2408 / 2568,7 = 0,937 (93,7%)
за февраль ie = 2431 / 2568,7 = 0,946 (94,6%) и т.д.
за июнь ie = 2703 / 2568,7 = 1,052 (105,2%)
за июль ie = 2822 / 2568,7 = 1,099 (109,9%) и т.д.
Степень силы сезонных колебаний измеряется средним квадратическим отклонением:
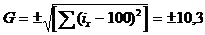 %
%
Задача 15. МЕТОД СГЛАЖИВАНИЯ РЯДА ДИНАМИКИ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ. Сгладим ряд динамики по трехлетней скользящей средней, так как период колебаний продажи равен трем годам.
Исчислим:
средний уровень за 1988 - 1990 гг.
__
У1  (ц)
(ц)
Средний уровень за 1989 - 1991 гг.
 У2
У2 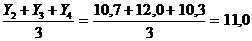 (ц)
(ц)
Средний уровень за 1990 - 1992 гг.
 У3
У3 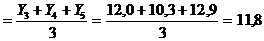 (ц) и т.д.
(ц) и т.д.
Результаты расчета трехлетней скользящей средней представлены в нижеследующей таблице:
| годы | Скользящая трехлетняя | Трехлетняя скользящая средняя | |
| А | 1 | 2 | 3 |
| 1988 | 10,0 (У1) | - | - |
| 1989 | 10,7 (У2) | 32,7 (У1 + У2 + У3) | 10,9 (У1) |
| 1990 | 12,0 (У3) | 33,0 (У2 + У3 + У4) | 11,0 (У2) |
| 1991 | 10,3 (У4) | 35,2 (У3 + У4 + У5) | 11,8 (У3) |
| 1992 | 12,9 (У5) | 39,5 (У4+ У5 + У6) | 13,2 (У4) |
| 1993 | 16,3 (У6) | 44,8 (У5 + У6 + У7) | 14,9 (У5) |
| 1994 | 15,5 (У7) | 49,7 (У6 + У7 + У8) | 16,6 (У6) |
| 1995 | 17,8 (У8) | 51,4 (У7 + У8 + У9) | 17,1 (У7) |
| 1996 | 18,0 (Уn) | - | - |
Полученные результаты (гр. 3) характеризуют рост урожайности.
МЕТОД АНАЛИТИЧЕСКОГО ВЫРАВНИВАНИЯ РЯДА ДИНАМИКИ ПО ПРЯМОЙ.
Уравнение прямой линии выражено формулой:
Уt = a0 +a1t
где Уt - значение выравненного ряда, которые нужно вычислить (теоретические уровни);
a0 и a1 - параметры прямой;
t - показатель времени (дни, месяцы, годы и т.д.)
Для нахождения параметров a0 и a1 необходимо решить систему нормальных уравнений:
a0 n + a1åt = åу
a0 åt + a1åt2 = åуt ,
где у - фактические уровни ряда динамики;
n - число уровней.
Для упрощения расчетов обозначим время так, чтобы начало отсчета времени приходилось на середину рассматриваемого периода:
| Годы | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
| t | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
Следовательно, å t = 0. тогда система нормальных уравнений примет вид:
a0 n = åу
a1åt2 = åуt ,
Отсюда a0 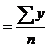 ; a1
; a1 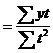 .
.
Расчет параметров a0 и a1
| Годы | Урожайность в ц с 1 га | Условные годы , t | t2 | уt | уt |
| A | 1 | 2 | 3 | 4 | 5 |
| 1988 | 10,0 | -4 | 16 | -40,0 | 9,30 |
| 1989 | 10,7 | -3 | 9 | -32,1 | 10,41 |
| 1990 | 12,0 | -2 | 4 | -24,0 | 11,52 |
| 1991 | 10,3 | -1 | 1 | -10,3 | 12,63 |
| 1992 | 12,9 | 0 | 0 | 0 | 13,74 |
| 1993 | 16,3 | 1 | 1 | 16,3 | 14,85 |
| 1994 | 15,6 | 2 | 4 | 31,2 | 15,96 |
| 1995 | 17,8 | 3 | 9 | 53,4 | 17,07 |
| 1996 | 18,0 | 4 | 16 | 72,0 | 18,18 |
| åу = 123,6 | åt = 0 | åt2 = 60 | +172,9 - 106,4 = ------------ åуt = 66,5 | å уt = 123,66 |
Следовательно,
a0  (руб.);
(руб.);
a1 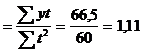 (руб.) . åt2
(руб.) . åt2
Таким образом, уравнение прямой имеет вид:
уt = 13,74 + 1,11 * t
Подставив в это уравнение значение t (гр.2), получим выравненные теоретически значения уt (гр.5).
Тема 5. ИНДЕКСЫ
ЗАДАЧИ
Задача 1. Известны следующие данные по предприятию:
| Себестоимость единицы млн.руб. | Выпуск продукции тыс. шт. | |||
| I квартал | IV квартал | I квартал | IV квартал | |
| Станок КС-5 | 5,3 | 5,0 | 2,0 | 2,4 |
| Станок КД-2 | 6,7 | 6,2 | 2,5 | 2,7 |
Определить индивидуальные и общие индексы себестоимости, количества и затрат на производство продукции.
Задача 2. Даны следующие сведения:
| Ткани | Общие затраты на производство за 1994 г., млн. руб. | Изменение количества выпуска в 1995 г. по сравнению с 1994 г. (в %) |
| Шелковые | 2800 | + 10 |
| Шерстяные | 2560 | - 10 |
Определить индивидуальные и общие индексы количества продукции (физического объёма).
Задача 3. На основе нижеприведённых данных рассчитать индивидуальные и общие индексы цен, количества и товарооборота:
| Цена за единицу продукции тыс. руб. | Количество проданной продукции тыс. кг. | |||
| I квартал | II квартал | I квартал | II квартал | |
| Молоко | 2,5 | 2,8 | 62000 | 62500 |
| Масло | 22,0 | 23,5 | 21000 | 22100 |
Задача 4. Количество проданных промышленных товаров в 1994 г. по сравнению с 1993 годом сократилось на 12%, а продовольственных за этот же период возросло на 5%. Товарооборот в 1993 г. по промышленным товарам составил 6400 млн. руб., а по продовольственным - 9100 мл. руб.. Определить общие индексы товарооборота и количества, если известно, что общий индекс цен составил 1,25.
Задача 5. Общие затраты на производство продукции в отчётном периоде по сравнению с базисным возросли на 15%, а себестоимость продукции за этот же период снизилась на 6%. Определить общий индекс физического объёма продукции.
Задача 6. По данным о продаже мяса на двух рынках рассчитайте индексы средней цены: а) переменного состава; б) фиксированного состава; в) индекс влияния структурных сдвигов:
| Номер | Январь | Июль | ||
| рынка | Цена за 1 кг в тыс. руб. | Продано в тыс. кг | Цена за 1 кг в тыс. руб. | Продано в тыс. кг |
| 1 | 7,0 | 600 | 8,1 | 680 |
| 2 | 7,2 | 400 | 8,4 | 420 |
Задача 7. Себестоимость изделия на предприятиии №1 в I квартале составила 4000 руб., на предприятии №2 - 4090 руб..Во втором квартале по сравнению с первым себестоимость изделия на предприятии № 1 возросла на 2%, а на предприятии №2 снизилась на 5%. Выпуск изделий на предприятии №1 во втором квартале составил 80 тыс. штук, на предприятии №2 - 65 тыс. штук. Средняя себестоимость изделия за этот же период возросла на 3%. Определить индексы средней себестоимости изделия фиксированного состава и влияния структурных сдвигов.
Задача 8. По условию задачи №6 определить общие индексы товарооборота, цен и количества продажи.
Задача 9. Оптовая цена на изделие А возросла на 5%, на изделие Б на 8%. Товарооборот после роста цен составил по изделию А - 200 млн. руб., по изделию Б 404 млн. руб.. Определить общий индекс цен.
Задача 10. Определить общие индексы себестоимости продукции, затраты на производство продукции и количества продукции по данным таблицы:
| Вид продукции | Общие затраты на производство продукции млн. р. | Снижение себестоимости единицы продукции в III квартале по сравнению с I кварталом | |
| I квартал | III квартал | ||
| Бязь | 3200 | 3300 | 2% |
| Ткань драпированная | 8400 | 9100 | 5% |
Задача 11. Известны данные о выпуске продукции и численность рабочих по двум предприятиям акционерного общества:
| Базисный год | Отчётный год | |||
| Объём продукции, млн. руб. | Число рабочих | Объём продукции, млн. руб. | Число рабочих | |
| Предприятие №1 | 169680 | 202 | 174345 | 194 |
| Предприятие №2 | 200700 | 223 | 208620 | 228 |
Рассчитать индивидуальные и общие индексы численности рабочих, объёма продукции и производительности труда.
Задача 12. По данным условия задачи №11 определить индексы производительности труда переменного, постоянного состава и влияния структурных сдвигов.
Задача 13. Определить общие индексы объёма продукции, производительности труда и численности рабочих по данным следующей таблицы:
| Акционерное общество | Объём продукции, млн. руб. | Изменение производительности труда во II квартале по сравнению с I | |
| I квартал | II квартал | ||
| Предприятие №1 | 1200 | 1300 | + 10% |
| Предприятие №2 | 1400 | 1485 | без изменения |
| Предприятие №3 | 1650 | 1840 | + 8% |
Задача 14. Общие затраты на производство женских сапог на обувной фабрике в 1993 г. составили 950 млн. руб., женских туфель - 630 млн. руб.. Количество произведённых сапог в 1994 г. по сравнению с 1993 г. возросло на 15%, а женских туфель на 20%. Общий индекс цен на продукцию фабрики составил 1,32. Рассчитать общий индекс количества продукции и индекс затрат на производство продукции.
Задача 15. Известны следующие данные по одному хозяйству:
| Культуры | Урожайность в ц с одного га | Посевная площадь, га | ||
| 1993 год | 1994 год | 1993 год | 1994 год | |
| Пшеница яровая | 20 | 22,5 | 200 | 230 |
| Ячмень | 19,8 | 21,4 | 180 | 150 |
Рассчитать индексы средней урожайности переменного, постоянного состава и влияния структурных сдвигов.
Задача 16. По условию задачи 15 определить общие индексы урожайности, посевных площадей и валового сбора.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ.
Задача 11. При индексном анализе значение качественного признака в отчётном периоде обозначим - х1, в базисном - х0, количественного признака соответственно f1 и f0, общего показателя x1f1 и x0f0. Тогда индивидуальные индексы производительности труда рассчитываются по схеме: ix=x1:x0, численности рабочих ix = f1:f0, объёма продукции ixf = x1f1:x0f0.
Так, по предприятию №1
i x 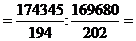 898,68:840 = 1,069 (106,9%)
898,68:840 = 1,069 (106,9%)
следовательно, производительность труда на предприятии № 1 возрасла на 6,9%.
if 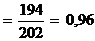 (96%) т.е. численность рабочих сократилась на 4%.
(96%) т.е. численность рабочих сократилась на 4%.
ixf  (102,7%) значит объём продукции на предприятии
(102,7%) значит объём продукции на предприятии
увеличился на 2,7%.
Соответствующие индексы по предприятию №2 будут равны
ix = 1,016, if = 1,022; ixf = 1,039.
Взаимосвязь индексов: ixf = ix * if
1,027=1,069 * 0,96
Общий индекс производительности труда исчисляется по формуле:
Jx = 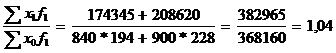 (104%)
(104%)
производительность труда по двум предприятиям в среднем возросла на 4%.
Общий индекс численности рабочих:
Jf = 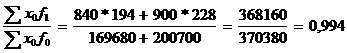 (99,4%)
(99,4%)
численность рабочих в отчётном году по сравнению с базисным сократилась на предприятиях в среднем на 0,6%.
Общий индекс продукции:
Jxf = 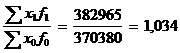 (103,4%)
(103,4%)
Общий объём продукции по акционерному обществу увеличился на 3,4%.
Взаимосвязь индексов: Jxf = Jx*Jf
Общий прирост объёма продукции:
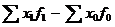 = 382965-370380 = + 12585 тыс. р.
= 382965-370380 = + 12585 тыс. р.
Этот прирост произошёл за счёт роста производительности труда
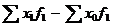 = 382965 - 368160 = + 24805 тыс.р.
= 382965 - 368160 = + 24805 тыс.р.
сокращение численности рабочих привело к снижению выпуска продукции
 = 368160 - 370380 = - 2220 тыс. р.
= 368160 - 370380 = - 2220 тыс. р.
Аналогично индексу производительности труда, строятся и другие индексы качественных показателей (себестоимости, цен, урожайности, заработной платы 1 рабочего и т. д..). По схеме индекса численности рабочих (Jf) вычисляются индексы продукции, посевных площадей и т. д.. Индексы товарооборота, фонда заработной платы, валового сбора и других объёмных показателей вычисляются по такой формуле как индекс объёма продукции (Jxf). Но наряду с использованием формул агрегатных индексов, базирующихся на исходных данных об абсолютных значениях качественных показателей (x) и количественных показателей (f), в статистике применяются и другие преобразованные формулы (см. задачи №2 и №9).
Задача 2. Индивидуальные индексы количества продукции составят:
ткани шёлковые : 100 + 10 = 110% (1,1)
ткани шерстяные 100 - 10 = 90% (0,9)
Общий индекс количества (физического объёма) по агрегатной форме:
Jf = 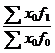 , используя индивидуальный индекс вычисляем: f1 = if * f0 и подставляем в числитель формулы:
, используя индивидуальный индекс вычисляем: f1 = if * f0 и подставляем в числитель формулы:
Jf = 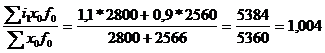 (100,4%)
(100,4%)
Количество произведённой продукции в 1995 г. возросло по сравнению с 1994 г. на 0,4%.
Задача 9. Индивидуальный индекс цен на изделие А составляет 105% (1,05), на изделие В - 108% (1,08). Общий индекс цен из агрегатной формы преобразуем в форму среднего гармонического индекса:



 Jx =
Jx = 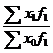 x0 =
x0 = 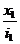 , J
, J 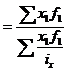


Jx  (1069%)
(1069%)
Таким образом, цены на продукцию возросли на 6,9%.
Задача 12. Индекс производительности труда переменного состава характеризует изменение средней производительности труда по АО вследствие влияния двух факторов: 1) изменения индивидуальной производительности треда на каждом предприятии; 2) структурных сдвигов в численности рабочих.



 Jперем = x1 : x0 =
Jперем = x1 : x0 = 


где x1 - выработка 1 рабочего в отчётном периоде (предприятие №1 - 174345: : 194 = 898,7 тыс. р., предприятие №2 - 208620 : 228 = 915 тыс. р.)
x0 - выработка 1 рабочего в базисном году (предприятие №1 - 169680 : 202 = 840 тыс. р., предприятие №2 200700 :223 = 900 тыс. р.)
f0,f1 - количество рабочих соответственно за базисный и отчётный год.
Jперем 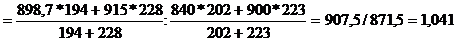
Таким образом, средняя производительность труда по АО возросла на 4,1%.
Индекс производительности труда фиксированного (постоянного) составил:
Jфикс = x1 : xусл 
= 907,5 :872,4 = 1,04 (104%)
следовательно, основным фактором динамики средней производительности является изменение выработки 1 рабочего на каждом предприятии, что привело к росту средней производительности труда на 4%.
Рассчитаем индекс производительности труда влияния структурных сдвигов.
Jвл. стр. сдв. = xусл. : x0 = 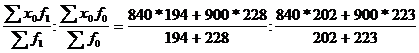
= 872,4 : 871,5 = 1,001 (100,1%)
Структурные сдвиги в численности рабочих были незначительны и привели к росту средней производительности труда на 0,1%.
Тема 6: ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
ЗАДАЧИ
Задача 1. Из партии 10000 штук в порядке механической выборки было обследовано 200 поршневых колец для определения их среднего веса.
Получены следующие данные об их весе:
Вес в г до 38 38 - 46 46 - 54 54 - 62
Число колец 22 84 75 19
Определить средний вес поршневого кольца в выборке и с вероятностью 0,954 установить пределы среднего веса колец во всей партии.
Задача 2. На ткацкой фабрике из 1000 ткачих в порядке случайной бесповторной выборки обследовано 100 человек. В результате обследования получены следующие данные о распределении ткачих по уровню дневной выработки:
Дневная выработка м 30 - 40 40 - 50 50 - 60 60 - 70
Число ткачих 30 28 27 15
По этим данным установите:
1) пределы значений средней дневной выработки одной ткачихи с вероятностью (0,954);
2) пределы значений доли ткачих фабрики с дневной выработкой 60 м с вероятностью 0,683 (0,954);
3) пределы средней дневной выработки одной ткачихи и доли ткачих с выработкой 60 м и более при случайном повторном отборе с вероятностью 0,683.
Задача 3. В сберегательных банках города в порядке механической выборки отобрали 10000 счетов вкладчиков и по ним установили средний размер вкладов в 2100 тыс. р. при коэффициенте вариации в 30%.
Какова вероятность того, что ошибка репрезентативности при определении размера вклада не превысит 3 тыс. р.?
Задача 4. Путём собственно-случайной бесповторной выборки проверено 5% деталей из партии в 500 деталей. Среди них оказалось 2% бракованных.
Определить границы, в которых заключена доля бракованных деталей во всей партии, гарантировав их с вероятностью 0,997.
Задача 5. Для изучения влияния общего стажа работы на квалификацию рабочих предприятия была проведена повторная типическая выборка с непропорциональным распределением (50 рабочих в каждой группе), которая дала следующие результаты:
| Группы рабочих по стажу работы | общее число рабочих | Объём выборки (человек) |
В том числе по разрядам | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| до 10 лет | 600 | 50 | 10 | 23 | 14 | 2 | 1 | - |
| свыше 10 лет | 400 | 50 | - | 5 | 8 | 17 | 14 | 6 |
| Итого | 1000 | 100 | 10 | 28 | 22 | 19 | 15 | 6 |
По этим данным определите:
1) возможные пределы среднего разряда рабочих предприятия с вероятностью 0,954;
2) возможные пределы доли рабочих на предприятии, имеющих высокую квалификацию (5-й и 6-й разряды), с вероятностью 0,683.
Задача 6. Из 100 ящиков по 400 деталей в каждом, поступивших в течении квартала на склад готовой продукции в порядке бесповторной серийной выборки отобрано 5 ящиков все детали которых проверены на вес. Были получены следующие результаты:
Ящики 1 2 3 4 5
Средний вес детали г 50 49 53 53 55
По этим данным установите возможные пределы среднего веса детали в ящиках, поступивших на склад с вероятностью 0,683.
Задача 7. В порядке случайной бесповторной выборки было отбрано 2% студентов. 15 человек из 60 сдали экзамены на отлично. С вероятностью 0,683 определите ошибку выборки и возможные пределы доли студентов вуза, сдавших экзамены на отлично.
Задача 8. Методом механической выборки на предприятии было отобрано 5% изделий. Результаты обследования характеризовались следующими данными:
% влажности количество
изделий изделий
до 2 30
2 - 4 8
4 - 6 10
6 и более 2
Определить с вероятностью 0,954 ошибку выборки и пределы в которых будет находится: а) средний процент влажности изделий; б) удельные вес изделий у которых влажность выше нормы, т-е выше 2%.
Задача 9. На предприятиях акционерного общества работает 500 рабочих по изготовлению одноимённой продукции. Из них со стажем работы до 5 лет работает 200 человек, более 5 лет - 300 человек. Для изучения производительности труда и установления доли квалифицированных рабочих проведена 10% - ная типическая выборка с отбором единиц пропорционально численности по указанным группам (внутри групп применялся случайный метод отбора).
На основе обследования получены следующие данные:
| Группы рабочих со стажем работы | Общее число рабочих, человек | Число обследованных рабочих, человек | Средняя дневная выработка штук | Дисперсия выработки | Число квалифицированных рабочих в выборке |
| До 5 лет | 200 | 20 | 22 | 36 | 16 |
| Свыше 5 лет | 300 | 30 | 28 | 25 | 27 |
| Итого | 500 | 50 | 25,6 |
Определить: а) с вероятностью 0,683 предельную ошибку выборки и границы в которых будут находится среднедневная выработка всех рабочих АО; б) с вероятностью 0,954 пределы удельного веса квалифицированных рабочих в общей численности рабочих АО.
Задача 10. В акционерном обществе из 12 цехов (с одинаковым количеством работающих) методом серийной выборки было отобрано 3 цеха для обследования. Распределение рабочих по проценту выполнения нормы выработки в этих цехах характеризовалось следующими данными:
| Цех | 1 | 2 | 3 |
| Число рабочих | 200 | 250 | 150 |
| Средний процент выполнения нормы выработки | 102 | 105 | 108 |
Определить: 1. С вероятностью 0,683 предельную ошибку репрезентативности на средний % выполнения нормы выработки; 2. С вероятностью 0,954 ошибку репрезентативности на долю рабочих, выполняющих норму выработки на 108%.
Задача 11. В результате исследования 20 проб молока поступившего на молокозавод определили, что средняя жирность молока 3,6% при среднем квадратическом отклонении 0,5%. Какова вероятность того, что возможная ошибка средней жирности поступившего молока более 0,3%?
Задача 12. Из 40000 вкладчиков сберегательного банка города методом пропорционального типического отбора по общественным группам было обследовано 2000 вкладчиков, которые по размеру вкладов распределились следующим образом:
Группы вкладчиков по размеру
Общественная вклада млн. р.
группа до 3 3 - 10 10 и более
рабочие 300 80 20
служащие 400 120 180
прочие 300 400 200
Определить: возможные пределы среднего вклада и доли вкладчиков с размером вклада до 3 млн. р. с вероятностью 0,954.
Задача 13. Проведено 10% механическое выборочное обследование студентов вуза и получены следующие результаты по уровню успеваемости:
успевающие 270 человек
неуспевающие 50 человек
С вероятностью 0,683 определить в каких пределах будет находится доля успевающих студентов всего вуза.
Задача 14. Имеются следующие данные о работе телеграфа: удельный вес срочных телеграмм 30%, среднее квадратическое отклонение по срокам их доставки составляло 12 минут, удельный вес обыкновенных телеграмм 70%, среднее квадратическое отклонение по срокам их доставки - 18 минут. Определите необходимую численность типической выборки с пропорциональным отбором по видам телеграмм, чтобы предельная ошибка средней скорости доставки телеграмм с вероятностью 0,683 не превышала 2 минут.
Задача 15. Какова должна быть численность повторной случайной выборки для определения доли студентов имеющих стаж работы по специальности, чтобы с вероятностью 0,997 ошибка репрезентативности не превышала 2%. Среднее квадратическое отклонение составляет 0,25.
Задача 16. По городскому маршруту автобусов было проведено выборочное обследование средней дальности поездки 600 пассажиров. На основе обследования была установлена средняя дальность поездки пассажира 2,2 км при среднем квадратичном отклонении 0,5 км.
С вероятностью 0,954 установить возможные пределы средней дальности поездки пассажиров.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Задача 8. Предельная ошибка выборки (ошибка репрезентативности) для всех видов выборочного наблюдения определяется по формуле:
D = ± t 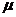
где 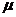 - средняя ошибка репрезентативности
- средняя ошибка репрезентативности
t - коэффициент доверия, он определяется величиной вероятности с которой хотят гарантировать результаты выборочного наблюдения.
В решениях задач данного практикума будут применяться значения вероятностей и коэффициентов доверия.
Вероятность (P) Коэффициент доверия (t)
 0,683 1
0,683 1
0,954 2
0,997 3
Средняя ошибка репрезентативности собственно-случайной и механической выборок определяется по нижеследующим формулам:
на средний размер признака
а) при повторном отборе mx = ± 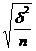
б) при бесповторном отборе mх 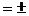
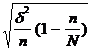
на долю признака 
а) при повторном отборе mW = ± 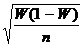
б) при бесповторном отборе mW = ± 
где N - численность генеральной совокупности
n - численность выборочной совокупности
d2 - ди сперсия признака в выборочной совокупности
W - доля единиц, обладающих признаком в выборке 
(1-W) - доля едениц, не обладающих данным признаком в выборке
Для определения пределов генеральной средней вычислить среднюю и дисперсию по выборочной совокупности. Расчёты приведены в таблице:
| % влажности изделий | Количество изделий f | Середина интервала х | xf | x-x | (x-x)2 | (x-x)2f |
| до 2,0 | 30 | 1 | 30 | - 1,36 | 1,8496 | 55,483 |
| 2 - 4 | 8 | 3 | 24 | - 0,64 | 0,4096 | 3,2768 |
| 4 - 6 | 10 | 5 | 50 | - 2,64 | 6,9696 | 69,696 |
| 6 и выше | 2 | 7 | 14 | - 4,64 | 21,5296 | 43,0592 |
| Итого | 50 | 118 | 171,52 |
x = 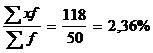
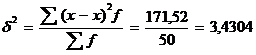
По данным условиям n = 50 N = 1000 ( 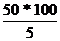 )
)
Средняя ошибка выборки при определении средней влажности изделий составит: 
mx = ± 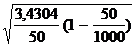 = ±
= ± 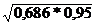 = ±
= ± 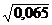 = ± 0,255%
= ± 0,255%
Предельная ошибка выборочной средней:
Dх = ± tm = ± 2 * 0,255 = 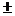 0,51%
0,51%
Следовательно, с вероятностью 0,954 можно утвердить, что средняя влажности изделий всей партии выпущенной продукции будет находится в пределах 2,36% ± 0,51%
Вычислим пределы удельного веса изделий, у которых влажность выше нормы, т-е выше 2% 

W  или 40%
или 40%
тогда DW 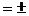 tm =
tm = 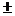 2
2  =
= 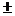 2
2 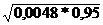
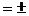 2
2 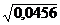 =
=
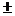 2 * 0,675 =
2 * 0,675 = 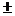 0,13 или 13%
0,13 или 13%
Таким образом, с вероятностью 0,954 можно утверждать, что удельный вес изделий, у которых влажность выше нормы в генеральной совокупности будет находиться в пределах (40 ±13)%.
Решение задачи №9
Средняя ошибка типической выборки определяется по формуле:
mx = ± 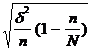
где 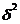 - средняя из внутригрупповых дисперсий. Она вычисляется по формуле:
- средняя из внутригрупповых дисперсий. Она вычисляется по формуле:

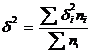
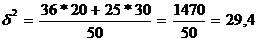
Тогда: mх = ± 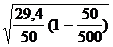 = ±
= ± 
Вычислим предельную ошибку выборки:
Dх = ± tmx = ± 1 * 7 = ± 0,7 года
с вероятностью 0,683 можно утверждать, что средняя дневная выработка всех рабочих АО будет находиться в пределах (25,6 ± 0,7) года.
Определим предельную ошибку репрезентативности на долю квалифицированных рабочих по формуле
D = ± tm = ± t 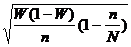
W = 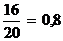 W =
W = 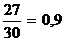
дисперсия доли рабочих со стажем до 5 лет
W(1 - W) = 0,8 * 0,2 = 0,16
дисперсия доли рабочих со стажем свыше 5 лет W (1 -W) = 0,9 * 0,1 = 0,09
Средняя дисперсия доли рабочих:
W(1 - W) = 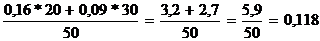
тогда DW = ±2 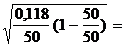 ± 0,09 или 9%
± 0,09 или 9%
Удельный вес квалифицированных рабочих в выборочной совокупности составит (16 + 27) : 50 = 0,86 или 86%
Следовательно, можно утверждать, что удельный вес квалифицированных рабочих во всей генеральной совокупности составит: (86 ± 9)%
Решение задачи 10.
Предельная ошибка репрезентативности на среднее значение признака при серийном отборе определяется по формуле:
Dx = ± t 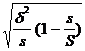
где s - число серий в выборочной совокупности;
S - число серий в генеральной совокупности.
Рассчитаем предварительно среднюю величину и дисперсию.
x = 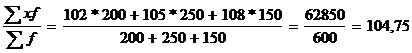
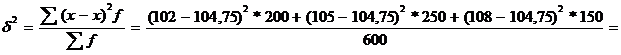
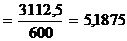
Dx = ± 1 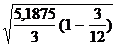 = ± 1
= ± 1 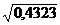 = ± 0,657
= ± 0,657
С вероятностью 0,683 можно утверждать, что средний процент выполнения норм выработки рабочими АО будет находиться в пределах (104,7± 0,657)%.
Предельная ошибка репрезентативности на долю признака при серийной выработке рассчитывается следующим образом:
DW = ± t 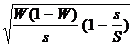
в данной задаче W = 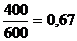 или 67%
или 67%
DW = ± 1  = ± 2
= ± 2 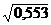 = ± 0,23 и
= ± 0,23 и
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
ЗАДАЧНИК
составитель Эльвира Ивановна Матыскина
ЛР №020262 от 30.10.91.
Подписано в печать 30.03.99. Формат 60х90 1/16. Бумага офсетная. Печать офсетная. Усл. печ. л. 3,6. Уч. - Изд. л. 3,3. Тираж 800 экз.
План1999 г. Поз 225 Заказ ... ПОП ИГЭА
Издательство Иркутской Экономической академии.
664015, Иркутск, ул. Ленина, 11
Дата добавления: 2018-02-15; просмотров: 2761; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
