Условие применения средних величин
Оглавление.
1. Введение………………………………………………. 2
2. Сущность и понятие статистики……………………... 3
3. Средние величины.
3.1 Определение средних величин……………………. 4
3.2 Условие применения средних величин……………4
3.3 Виды средних величин. …………………………… 6
3.3.1 Степенные средние……………………………. 6
3.3.2 Структурные средние…………………………. 10
4. Заключение…………………………………………….. 13
5. Список литературы…………………………………….14
Введение
В данной работе рассмотрим такое понятие, как средние величины. Большое распространение в статистике имеют средние величины. В средних величинах отображаются важнейшие показатели товарооборота, товарных запасов, цен. Средними величинами характеризуются качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др. Правильное понимания сущности средней определяет ее особую значимость в условиях рыночной экономики. Когда средняя через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития.
Актуальность темы заключается в том, что область применения и использования средних величин в статистике довольно широка.
Цель - ознакомление с применением средних величин в статистике.
Задачи: 1)раскрыть сущность и понятие статистики.
2)дать определение средних величин и виды средних величин.
|
|
|
Сущность и понятие статистики
Термин «статистика» происходит от латинского слова «статус», которое означает «положение, порядок». Впервые его употребил немецкий ученный Ахенваль (1719-1772).
Статистика- наука, изучающая положение дел в государстве. Иными словами, это вид деятельности, направленной на получение, обработку и анализ информации, характеризирующий количественные закономерности жизни общества во всем их многообразии в неразрывной связи с ее качественным содержанием. Под статистикой понимается сбор цифровых данных, их обобщение и обработка.
В более узком смысле статистика рассматривается как совокупность данных о каком-либо явлении или процессе. В естественных науках понятие статистика означает анализ массовых явлений, основанный на применении методов теории вероятности.
Содержание дисциплины «статистика» включает определение предмета изучения статистики, а также знакомство с методами сбора, обработки и представления данных, анализа и интерпретации результатов.
Основные положения статистики, с одно стороны базируются на законах социальной и экономической теории, так как именно они рассматривают закономерности развития общественных явлений, определяя их значение, причины и последствия для жизни общества. С другой стороны, законы многих общественных наук построены на основании показателей статистики
|
|
|
и закономерностей, определенных с помощью статистического анализа. Таким образом, статистика определяет законы общественных наук, а они в свою очередь корректируют положения статистики.
Средние величины
Определение средних величин
Средняя величина - обобщающий показатель большого количества индивидуальных значений варьирующего признака. Т. е то общее, что характерно для всей совокупности, но исключает те отличия, которые наблюдаются у отдельных единиц, как бы взаимно погашая их.
Средние величины являются одними изнаиболее распространенных обобщающих статистических показателей. Они имеютсвоей целью одним числом охарактеризовать статистическую совокупность, состоящуюиз меньшинства единиц. Средние величины тесно связаны с законом больших чисел.Сущность этой зависимости заключается в том, что при большом числе наблюденийслучайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.
|
|
|
Средняя является объективной характеристикой только для однородных явлений. Средние для неоднородных совокупностей называются огульными и могут применяться только в сочетании с частными средними однородных совокупностей.
Средняя является объективной характеристикой только для однородных явлений. Средние для неоднородных совокупностей называются огульными и могут применяться только в сочетании с частными средними однородных совокупностей.
Условие применения средних величин
Как уже говорилось выше, обязательным условием расчета средних величин для исследуемой совокупности является ее однородность. Действительно, допустим, что отдельные элементы совокупности, вследствие подверженности влиянию некоторого случайного фактора, имеют слишком большие (или слишком малые) величины изучаемого признака, существенно отличающиеся от остальных. Такие элементы повлияют на размер средней для данной совокупности, поэтому средняя не будет выражать наиболее характерную для совокупности величину признака.
Если исследуемое явление не является однородным, то его разбивают на группы, содержащие только однородные элементы. Для такого явления рассчитываются сначала средние по группам, которые называются групповые средние, – они будут выражать наиболее типичную величину явления в каждой группе. Затем рассчитывается для всех элементов общая средняя величина, характеризующая явление в целом, – она рассчитывается как средняя из групповых средних, взвешенных по числу элементов совокупности, включенных в каждую группу. На практике, однако, безусловное выполнение данного условия повлекло бы за собой ограничение возможностей статистического анализа общественных процессов. Поэтому, часто средние величины рассчитываются по неоднородным явлениям.
|
|
|
Еще одним важным условием применения средних величин в анализе является достаточное количество единиц в совокупности, по которой рассчитывается среднее значение признака. Достаточность анализируемых единиц обеспечивается корректным определением границ исследуемой совокупности, т.е. закладывается еще на начальном этапе статистического исследования. Данное условие становится решающим при применении выборочного наблюдения, когда необходимо обеспечить репрезентативность выборки.
Определение максимального и минимального значения признака в изучаемой совокупности также является условием применения средней величины в анализе. В случае больших отклонений между крайними значениями и средней, необходимо проверить принадлежность экстремумов к исследуемой совокупности. Если сильная изменчивость признака вызвана случайными, кратковременными факторами, то, возможно, крайние значения не характерны для совокупности. Следовательно, их следует исключить из анализа, т.к. они оказывают влияние на размер средней величины.
Виды средних величин
Все средние величины делятся на два больших класса:
1) степенные средние; к ним относятся такие известные и часто применяемые виды, средняя гармоническая, средняя геометрическая средняя квадратическая и средняя кубическая;
2) структурные средние величины, в качестве которых рассматриваются мода и медиана.
Средняя арифметическая.
Среднее арифметическое– среднее слагаемое
Средняя арифметическая простая - равна сумме отдельных значений признака, деленной на число этих значений.
Следовательно, средняя арифметическая простая равна:

Например: Рассчитаем среднюю арифметическую на основании условных данных по 10 магазинам, входящим в торговую фирму, (табл.)
| Мага-зины | Порядковый номер магазинов | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| S ма-газина | 60 | 80 | 40 | 100 | 60 | 70 | 50 | 120 | 100 | 60 |


Таким образом, средняя площадь магазинов по этой группе торговых предприятий составляет 74 кв.м.
Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.
Средняя арифметическая взвешенная - равнасумме произведений признака на вес, деленной на сумму веса.
Формула средней арифметической взвешенной:

Пример. Найти среднюю заработную плату рабочих цеха за месяц
| Заработная плата одного рабочего руб.; X | Число рабочих F |
| 32000 | 20 |
| 33000 | 35 |
| 34000 | 14 |
| 40000 | 6 |
| Итого: | 75 |
Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

3.3.1Степенные средние величины.
Средняя гармоническая.
Среднее гармоническое – рассчитывается тогда когда по условиям задачи необходимо, чтобы неизменной оставалась при осреднение сумма величин, обратных индивидуальным значениям признака.
Средняя гармоническая применяется в тех случаях, когда частоты(веса) не приводятся непосредственно, а вхдят сомножителями в один из имеющихся показателей.
Средняя гармоническая простая - отношение числа вариантов к сумме обратных значений этих вариантов.
И расчитывается по формуле:

Пример. Автомобиль доставил товары в три магазина фирмы, которые удалены от головного предприятия на одинаковое расстояние. Так, до первого магазина, расоложенного на шоссейной дороге, автомобиль прошел путь со скоростью 50 км/ч, до второго, по проселочной дороге, -40 км/ч , а в третьем случае автомобилю пришлось полпуи пройти через лесной массив, и скорость движения составила только 30 км/ч.
Расчитаем среднюю.

Среднее гармоническое взвешенное- равнасумме объемов признаков деленная на сумму отношения объема к признаку.

Прмер.Расчитатьиздержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
| Номер завода | Издержки производства, тыс.руб. | Себестоимость единицы продукции, руб. |
| 1 | 200 | 20 |
| 2 | 460 | 23 |
| 3 | 110 | 22 |
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.
 руб.
руб.
Средняя геометрическая.
Среднее геометрическое – применяется, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин.
Средняя геометрическаяприменяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическая простая –
Формула геометрической простой:

Средняя геометрическая взвешенная -
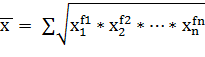
Например, в результате инфляции за первый год цена возросла в 2 раза к предыдущему году, а за второй год еще в 3 раза к уровню предыдущего года.
Ясно, что за 2 года цена выросла в 6 раз. По арифметической то было бы  за год, а за два 2,5*2,5= 6,25, а не в 6 раз. То геометрическая дает правильный результат
за год, а за два 2,5*2,5= 6,25, а не в 6 раз. То геометрическая дает правильный результат  раза.
раза.
Средняя квадратическая.
Среднее квадратическое – применяется, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.
Формула средней квадротической простой:
 .
.
Формула средней квадротической взвешенной:

Например, имеются три участка земельной площади со сторонами квадрата: х1 = 100 м; х2 = 200 м; х3 = 300 м.

Кубическая средняя.
Среднее кубическое– применяется, если надо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину.
Формула средней кубической простой:
 .
.
Формула средней кубической взвешенной:

3.3.2 Структурные средние величины.
Мода - применяется при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.
При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем - значение модальной величины признака по формуле:

где:
· М0 - значение моды
· х0 - нижняя граница модального интервала
· h - величина интервала
· fm - частота модального интервала
· fm-1 - частота интервала, предшествующего модальному
· fm+1 - частота интервала, следующего за модальным
Медиана -это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот Σfi/2, а зетем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем - значение медианы по формуле:

где:
· Me - искомая медиана
· х0 - нижняя граница интервала, который содержит медиану
· h - величина интервала
· Σfi - сумма частот или число членов ряда
· Sm-1 - сумма накопленных частот интервалов, предшествующих медианному
fm - частота медианного интервала
Пример. Найти моду и медиану.
| Возрастные группы | Число студентов | Сумма накопленных частот ΣS |
| До 20 лет | 346 | 346 |
| 20 - 25 | 872 | 1218 |
| 25 - 30 | 1054 | 2272 |
| 30 - 35 | 781 | 3053 |
| 35 - 40 | 212 | 3265 |
| 40 - 45 | 121 | 3386 |
| 45 лет и более | 76 | 3462 |
| Итого | 3462 |
Рассчитаем величину моды:
 =27 лет
=27 лет
Расчитает величину медианы:

Заключение.
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Средние величины делятся на два больших класса: степенные средние, структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая, средняя гармоническая, средняя кубическая.
В качестве структурных средних рассматриваются мода и медиана.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным. Взвешенная средняя считается по сгруппированным данным.
Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым. Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины.
Список литературы
Дата добавления: 2018-02-15; просмотров: 5242; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
