Абсолютное значение одного процента прироста
| Год | Цепные |
| 2003 | - |
| 2004 | 0,4 / 05 = 0,08 млн. руб., или 8,0 / 100 = 0,08 млн. руб. |
| 2005 | 0,5 / 5,9 = 0,084 млн. руб., или 8,4 / 100 = 0,084 млн. руб. |
| и т.д. |
Исчисленные выше аналитические показатели ряда динамики представлены в таблице.
2. Среднегодовой абсолютный прирост:
 млн. руб.
млн. руб.
или
 млн. руб.
млн. руб.
Среднегодовой темп роста:

или

Среднегодовой темп прироста:

3. Средний уровень ряда динамики находим по формуле средней арифметической простой, так как представленный ряд - интервальный с равными интервалами времени (один год):
 млн. руб.
млн. руб.
Таким образом, производство продукции на предприятии ежегодно возрастало. За 2003-2008 гг. абсолютный прирост составил 2,8 млн. руб. Темп роста за этот период составил 135%, темп прироста - 35%. В среднем за год абсолютный прирост составил 0,56 млн. руб., а среднегодовой темп прироста - 6,2%, т.е. производство продукции ежегодно увеличивалось в среднем на 0,56 млн. руб., или на 6,2%. Значение 1% прироста также возросло с 80 до 101 тыс. руб.
Динамика производства продукции предприятия за 2003-2008 гг.
| Год | Продукция | Абсолютные | Темпы | Темпы | Абсолютное | |||
| базисные | цепные | базисные | цепные | базисные | цепные | |||
| 2003 | 8,0 | 0 | - | 100,0 | - | 0 | - | - |
| 2004 | 8,4 | 0,4 | 0,4 | 105,0 | 105,0 | 5,0 | 5,0 | 80 |
| 2005 | 8,9 | 0,9 | 0,5 | 111,2 | 105,9 | 11,2 | 5,9 | 84 |
| 2006 | 9,5 | 1,5 | 0,6 | 118,7 | 106,7 | 18,7 | 6,7 | 89 |
| 2007 | 10,1 | 2,1 | 0,6 | 126,2 | 106,3 | 26,2 | 6,3 | 95 |
| 2008 | 10,8 | 2,8 | 0,7 | 135,0 | 106,9 | 35,0 | 6,9 | 101 |
|
|
|
Пример решения задачи 6
I. Имеются следующие данные об остатках материалов на складе предприятия, тыс. руб.:
на 1 января - 400;
на 1 февраля - 455;
на 1 марта - 465;
на 1 апреля - 460.
Определите среднемесячный остаток материалов на складе за I квартал.
Решение
По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда исчисляется по формуле средней хронологической простой:

Среднемесячный остаток материалов на складе за I квартал составил 450 тыс. руб.
II. Имеются следующие данные о товарных запасах розничного торгового предприятия, тыс. руб.:
на 1 января 2007 г. - 61,1;
на 1 мая 2007 г. - 57,5;
на 1 августа 2007 г. - 51,3;
на 1 января 2008 г. - 61,1.
Вычислите среднегодовой запас розничного торгового предприятия за 2007 г.
Решение
Для моментного ряда динамики с неравными интервалами средний уровень ряда исчисляется по формуле средней хронологической взвешенной:

где 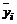 - средние уровни в интервале между датами;
- средние уровни в интервале между датами;
 - величина интервала времени (число месяцев между моментами времени).
- величина интервала времени (число месяцев между моментами времени).
В нашем примере число месяцев между моментами времени составило соответственно 4, 3, 5.
|
|
|
Итак, средний уровень товарных запасов

Задачи 7-8 охватывают один из наиболее сложных разделов теории статистики. Индексный метод анализа является одним из основных методов статистического изучения социально-экономических явлений. При выполнении заданий по этой теме необходимо понять сущность индексов (индивидуального и общего). Общие индексы могут исчисляться в агрегатной форме и как средние индексы (в средней арифметической и средней гармонической формах). Выбор формы индексов зависит от имеющихся исходных данных задачи.
Индивидуальные индексы рассчитываются следующим образом:
· индивидуальные индексы цены:  ;
;
· индивидуальные индексы физического объема;  .
.
Общие индексы в агрегатной форме:
· индекс цен 
· индекс физического объема 
· индекс стоимости (товарооборота) 
Разность числителя и знаменателя индекса цен показывает дополнительные расходы населения при увеличении цен на товары и услуги или экономию у населения денежных средств в случае снижения цен.
Индекс физического объема может быть представлен в средней арифметической форме:

Индекс цен может быть вычислен по средней гармонической формуле:
|
|
|

Индексный метод анализа позволяет также изучить динамику средней величины качественного показателя. Относительное изменение средней величины такого показателя (например, цены) называют индексом переменного состава:

Данный индекс отражает влияние двух факторов:
1) изменение индексируемого показателя у отдельных объектов (частей совокупности);
2) изменение удельного веса этих частей в общей совокупности (структурные сдвиги).
Влияние первого фактора определяется с помощью индексов постоянного (фиксированного) состава:

Влияние второго фактора - с помощью индекса влияния структурных сдвигов:

При вычислении индексов можно использовать системы взаимосвязанных индексов:
1) товарооборота:
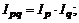
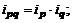
2) переменного состава, постоянного (фиксированного) состава и структурных сдвигов:
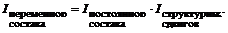
На основе данных систем по двум известным индексам исчисляется третий (неизвестный) индекс и выполняется факторный анализ изменений товарооборота (1) и среднего показателя (2).
Пример решения задачи 7
I. Имеются следующие данные о продаже товаров в магазине за два квартала года:
|
|
|
| Товар | Товарооборот | Изменение количества | |
| I квартал | II квартал | ||
| p0q0 | p1q1 | ||
| Овощи | 600 | 640 | -20 |
| Мясопродукты | 420 | 440 | +10 |
| Масло растительное | 350 | 380 | Без изменения |
Вычислите:
1) общий индекс товарооборота;
2) общий индекс физического объема товарооборота;
3) общий индекс цен.
Решение
1. Общий индекс товарооборота равен:

Товарооборот во II квартале по сравнению с I кварталом вырос на 6,6%. Абсолютный прирост товарооборота составил 90 тыс. руб. (1460-1370).
2. Общий индекс физического объема товарооборота вычислим по формуле среднего арифметического индекса, который тождествен агрегатной форме индекса:

Для вычисления данного индекса определим предварительно индивидуальные индексы количества проданного товара:
· для овощей: 100-20=80%, или 0,80 (  );
);
· для мясопродуктов: 100+10=110%, или 1,10 (  );
);
· для масла растительного: 100%, или 1 (  ).
).

т.е. физический объем товарооборота в среднем снизился на 5,7%.
В результате изменения физического объема продаж товарооборот уменьшился на 78 тыс. руб. (1292-1370).
3. Общий индекс цен может быть исчислен с помощью взаимосвязи индексов:

Следовательно,  или 110,3%, т.е. цены в среднем возросли на 10,3%. За счет роста цен товарооборот увеличился на 168 тыс. руб. (1460-1292).
или 110,3%, т.е. цены в среднем возросли на 10,3%. За счет роста цен товарооборот увеличился на 168 тыс. руб. (1460-1292).
II. Имеются следующие данные о продаже обуви в магазине города:
| Вид товара | Стоимость проданной обуви в IV квартале, тыс. руб. | Индексы цен на обувь в IV квартале по сравнению с III кварталом |
| p1q1 | ip | |
| Туфли женские | 350 | 1,20 |
| Ботинки мужские | 280 | 0,95 |
Определите изменение цен на проданную обувь в IV квартале по сравнению с III кварталом.
Решение
Общий индекс цен вычисляем по формуле среднего гармонического индекса, тождественного агрегатной форме индекса:

или 107,4%.
То есть цены в среднем возросли на 7,4%.
Пример решения задачи 8
Имеются следующие данные о выпуске продукции "А" по двум заводам:
| Номер завода | Базисный период | Отчетный период | ||||
| Произведено продукции, тыс. шт. | Себестоимость единицы, руб. | Удельный вес продукции, % | Произведено продукции, тыс. шт. | Себестоимость единицы, руб. | Удельный вес продукции, % | |
| q0 | z0 | d0 | q1 | z1 | d1 | |
| 1 | 60 | 24 | 50 | 80 | 20 | 40 |
| 2 | 60 | 20 | 50 | 120 | 18 | 60 |
| 120 | 100 | 200 | 100 | |||
Вычислите индексы себестоимости переменного, постоянного состава и влияния структурных сдвигов.
Решение
Вычислим индекс себестоимости переменного состава, который характеризует динамику средней себестоимости по двум заводам:

Средняя себестоимость продукции по двум заводам в отчетном и базисном периодах равна:


Следовательно, индекс себестоимости переменного состава равен:

Индекс показывает, что средняя себестоимость изделия по двум заводам снизилась на 14,5%. Это снижение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры производства продукции (удельного веса продукции отдельных заводов).
Влияние первого фактора на динамику средней себестоимости выявим с помощью индекса себестоимости постоянного состава:

Себестоимость продукции по двум заводам в среднем снизилась на 13%.
Влияние второго фактора характеризуется индексом структурных сдвигов:

Средняя себестоимость изделия в отчетном периоде снизилась
дополнительно на 1,8% за счет изменения структуры производства, т.е. за счет увеличения доли продукции второго завода с более низкой себестоимостью продукции с 50 до 60%.
ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ
Вариант 1
Задача 1
Имеются следующие данные по совокупности предприятий:
| Номер предприятия | Среднесписочная численность работников, чел. | Объем продукции, млн. руб. | Номер предприятия | Среднесписочная численность работников, чел. | Объем продукции, млн. руб. |
| 1 | 200 | 2,9 | 16 | 400 | 9,8 |
| 2 | 220 | 3,0 | 17 | 402 | 7,2 |
| 3 | 260 | 3,3 | 18 | 460 | 10,0 |
| 4 | 280 | 4,0 | 19 | 312 | 3,8 |
| 5 | 310 | 4,3 | 20 | 420 | 9,2 |
| 6 | 200 | 2,9 | 21 | 370 | 9,1 |
| 7 | 210 | 3,2 | 22 | 440 | 9,4 |
| 8 | 260 | 3,9 | 23 | 302 | 5,3 |
| 9 | 220 | 4,0 | 24 | 405 | 9,5 |
| 10 | 306 | 4,4 | 25 | 243 | 3,5 |
| 11 | 304 | 6,6 | 26 | 408 | 5,5 |
| 12 | 180 | 4,2 | 27 | 272 | 5,3 |
| 13 | 212 | 4,3 | 28 | 413 | 7,9 |
| 14 | 400 | 8,2 | 29 | 302 | 5,6 |
| 15 | 480 | 9,0 | 30 | 395 | 6,8 |
С целью изучения зависимости между численностью работников и объемом выпускаемой продукции произведите группировку предприятий по численности работников, выделив пять групп с равными интервалами; по каждой группе и в целом по совокупности подсчитайте:
а) число предприятий;
б) среднесписочную численность работников - всего и в среднем на одно предприятие;
в) объем продукции - всего и в среднем на одно предприятие.
Полученные результаты представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
По плану объем продаж АО в 2009 г. должен увеличиться на 5 млн. руб. Фактически объем продаж в сопоставимых ценах вырос по сравнению с 2008 г. на 5,5% и составил 146 млн. руб.
Определите относительную величину планового задания и выполнения плана.
Задача 3
Имеются следующие данные о посевной площади, валовом сборе и урожайности озимой пшеницы по хозяйству:
| Номер бригады | Базисный период | Отчетный период | ||
| Урожайность, ц/га | Посевная площадь, га | Урожайность, ц/га | Валовой сбор, ц | |
| 1 | 20,5 | 250 | 21,4 | 53 500 |
| 2 | 21,3 | 260 | 22,0 | 61 600 |
| 3 | 23,6 | 290 | 25,2 | 75 600 |
Определитесреднюю урожайность озимой пшеницы по хозяйству за каждый период. Укажите, какие виды средних применялись, обоснуйте выбор формы средней.
Задача 4
Имеются следующие данные о распределении работников фирмы по размеру среднемесячной заработной платы:
| Группа работников по размеру заработной платы, тыс. руб. | Численность работников |
| До 12 | 6 |
| 12-13 | 9 |
| 13-14 | 13 |
| 14-15 | 27 |
| 15-16 | 43 |
| 16-17 | 33 |
| 17-18 | 15 |
| 18 и более | 4 |
| Итого | 150 |
Для характеристики дифференциации работников по размеру среднемесячной заработной платы рассчитайте:
1) моду и медиану;
2) коэффициент вариации.
Сделайте выводы.
Задача 5
Имеются следующие данные о жилищном фонде региона (на конец года), тыс. м2:
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 |
| Жилищный фонд | 2710 | 2738 | 2761 | 2787 | 2818 |
Определите:
1) средний уровень ряда динамики;
2) цепные и базисные абсолютные приросты;
3) среднегодовые темпы роста и прироста.
Задача 6
Списочная численность работников фирмы в 2009 г. составила: на 1 января - 530 чел., на 1 марта - 570 чел., на 1 июня - 520 чел., на 1 сентября - 430 чел., а на 1 января 2008 г. - 550 чел.
Вычислите среднегодовую численность работников фирмы за 2009 г.
Задача 7
Имеются следующие данные о товарообороте магазина:
| Товарная группа | Продано товаров в фактических ценах, тыс. руб. | |
| Базисный период | Отчетный период | |
| Трикотажные изделия | 480 | 505 |
| Чулочно-носочные изделия | 130 | 190 |
В отчетном периоде по сравнению с базисным количество продаж по трикотажным изделиям возросло на 5 %, по чулочно-носочным изделиям снизилось на 7%.
Определите:
1) общий индекс товарооборота в фактических ценах;
2) общий индекс физического объема продаж;
3) общий индекс цен, используя взаимосвязь индексов.
Задача 8
Продажа яблок на двух рынках города характеризуется следующими данными:
| Рынок | Июль | Август | ||
| Объем продаж, тыс. кг | Цена 1 кг, руб. | Объем продаж, тыс. кг | Цена 1 кг, руб. | |
| 1 | 40 | 18,0 | 48 | 16,0 |
| 2 | 40 | 24,0 | 32 | 18,0 |
Определите:
1) индексы цен для отдельных рынков;
2) индексы цен переменного, постоянного состава и влияния структурных сдвигов.
Поясните смысл исчисленных индексов.
Вариант 2
Задача 1
Имеются следующие данные по совокупности предприятий:
| Номер предприятия | Среднегодовая стоимость основных фондов, млн. руб. | Объем продукции, млн. руб. | Номер предприятия | Среднегодовая стоимость основных фондов, млн. руб. | Объем продукции, млн. руб. |
| 1 | 8,0 | 8,4 | 16 | 7,9 | 12,9 |
| 2 | 16,0 | 20,8 | 17 | 11,3 | 9,2 |
| 3 | 10,2 | 11,6 | 18 | 7,0 | 8,3 |
| 4 | 9,8 | 10,6 | 19 | 6,0 | 7,5 |
| 5 | 12,6 | 16,0 | 20 | 10,8 | 17,0 |
| 6 | 15,0 | 18,8 | 21 | 4,0 | 3,6 |
| 7 | 13,2 | 22,4 | 22 | 8,9 | 9,2 |
| 8 | 6,5 | 6,8 | 23 | 9,6 | 10,4 |
| 9 | 13,4 | 14,0 | 24 | 11,8 | 18,0 |
| 10 | 6,8 | 5,7 | 25 | 5,4 | 6,2 |
| 11 | 6,6 | 6,7 | 26 | 10,2 | 14,4 |
| 12 | 7,8 | 10,9 | 27 | 6,9 | 5,4 |
| 13 | 8,2 | 9,9 | 28 | 5,0 | 6,0 |
| 14 | 11,8 | 14,0 | 29 | 13,0 | 14,5 |
| 15 | 12,8 | 15,7 | 30 | 8,4 | 9,6 |
С целью изучения зависимости между среднегодовой стоимостью основных фондов и объемом продукции произведите группировку предприятий по стоимости основных фондов, выделив четыре группы с равными интервалами; по каждой группе и в целом подсчитайте:
а) число предприятий;
б) среднегодовую стоимость основных фондов - всего и в среднем на одно предприятие;
в) стоимость продукции - всего и в среднем на одно предприятие;
г) объем продукции в расчете на один рубль основных фондов (фондоотдачу).
Полученные результаты представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
Имеются следующие данные о динамике товарооборота продовольственных и непродовольственных товаров по региону, млн. руб.:
| Товары | Базисный период | Отчетный период |
| Продовольственные | 11 502,0 | 12 215,1 |
| Непродовольственные | 18 045,5 | 17 702,6 |
Определитедля каждого периода:
1) относительные показатели структуры розничного товарооборота;
2) относительные величины координации.
Сделайте выводы.
Задача 3
Имеются следующие данные по двум машиностроительным заводам:
| Номер | I квартал | II квартал | ||
| План выпуска продукции, тыс. руб. | Процент выполнения плана | Фактический выпуск продукции, тыс. руб. | Процент выполнения плана | |
| 1 | 900 | 108 | 990 | 110 |
| 2 | 600 | 95 | 686 | 98 |
Определите за каждый квартал процент выполнения плана выпуска продукции в среднем по обоим заводам.
Задача 4
Имеются следующие данные о распределении кредитных организаций региона по величине уставного капитала:
| Уставный капитал, млн. руб. | Число организаций, % к итогу |
| До 20 | 12,3 |
| 20-40 | 14,1 |
| 40-60 | 20,8 |
| 60-80 | 16,7 |
| 80-100 | 15,2 |
| 100-120 | 13,6 |
| 120 и выше | 7,3 |
| Итого | 100 |
Для характеристики дифференциации кредитных организаций по величине уставного капитала рассчитайте:
1) средний размер уставного капитала;
2) моду и медиану;
3) первую и девятую децили и децильный коэффициент дифференциации.
Сделайте выводы.
Задача 5
Производство электроэнергии в регионе в 2005-2009 гг. характеризуется следующими данными, млрд. кВт·ч:
| 2005 г. | 2006 г. | 2007 г. | 2008 г. | 2009 г. |
| 1150 | 1202 | 1239 | 1294 | 1302 |
Рассчитайте:
1) базисные и цепные абсолютные приросты;
2) базисные и цепные темпы роста и прироста;
3) среднегодовое производство электроэнергии в регионе в 2004-2008 гг.
Результаты расчетов изложите в табличной форме. Сделайте выводы.
Задача 6
Имеются следующие данные о среднесписочной численности работников предприятия оптовой торговли, чел.:
Январь - 263
Февраль - 265
Март - 267
Второй квартал - 280
Второе полугодие - 277
Определитесреднесписочную численность работников предприятия за год.
Задача 7
Продажа сельскохозяйственных продуктов на рынке города характеризуется следующими данными:
| Продукт | Цена, руб./кг | Объем продаж, тыс. кг | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| Мясо говяжье | 180,0 | 200,0 | 150 | 180 |
| Мясо свиное | 220,0 | 250,0 | 120 | 130 |
| Птица | 70,0 | 90,0 | 20 | 15 |
Определите:
1) общие индексы цен, физического объема продаж и стоимости товарооборота в фактических ценах, покажите их взаимосвязь;
2) абсолютное изменение товарооборота - общее, в том числе за счет изменения цен и физического объема продаж.
Задача 8
Имеются следующие данные о производстве однородной продукции по двум заводам:
| Завод | Выработано продукции, | Затраты на продукцию, | ||
| 2008 г. | 2009 г. | 2008 г. | 2009 г. | |
| 1 | 12 | 20 | 48 | 60 |
| 2 | 16 | 17 | 80 | 68 |
Вычислите:
1) индекс себестоимости переменного состава;
2) индекс себестоимости постоянного состава;
3) индекс влияния структурных сдвигов.
Покажите взаимосвязь исчисленных индексов. Поясните полученные результаты.
Вариант 3
Задача 1
Имеются следующие данные по торговым предприятиям:
| Номер предприятия | Товарооборот, млн. руб. | Издержки обращения, млн. руб. | Номер предприятия | Товарооборот, млн. руб. | Издержки обращения, млн. руб. |
| 1 | 7,5 | 1,0 | 16 | 9,2 | 1,1 |
| 2 | 9,0 | 1,0 | 17 | 4,8 | 0,5 |
| 3 | 6,8 | 0,9 | 18 | 15,2 | 1,9 |
| 4 | 15,7 | 1,4 | 19 | 4,8 | 0,6 |
| 5 | 11,7 | 1,2 | 20 | 18,6 | 2,6 |
| 6 | 4,0 | 0,4 | 21 | 5,0 | 0,7 |
| 7 | 5,6 | 0,5 | 22 | 7,4 | 1,1 |
| 8 | 15,0 | 1,5 | 23 | 3,6 | 0,5 |
| 9 | 7,1 | 0,8 | 24 | 6,8 | 0,7 |
| 10 | 14,0 | 2,3 | 25 | 17,2 | 2,8 |
| 11 | 7,8 | 1,4 | 26 | 11,6 | 1,6 |
| 12 | 10,7 | 1,4 | 27 | 16,1 | 1,2 |
| 13 | 14,9 | 1,9 | 28 | 13,1 | 2,0 |
| 14 | 12,1 | 1,7 | 29 | 11,4 | 1,1 |
| 15 | 6,5 | 1,0 | 30 | 14,8 | 1,8 |
С целью изучения зависимости между объемом товарооборота и величиной издержек обращения произведите группировку предприятий по объему товарооборота, выделив пять групп с равными интервалами; по каждой группе и в целом по совокупности подсчитайте:
а) число предприятий;
б) объем товарооборота - всего и в среднем на одно предприятие;
в) величину издержек обращения - всего и в среднем на одно предприятие.
Полученные результаты представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
В базисном году объем грузооборота автотранспортного предприятия составил 210,0 млн. т·км. Планом текущего года было предусмотрено увеличить объем грузооборота на 10,5 млн. т·км.; фактически объем грузооборота в текущем периоде составил 230,3 млн. т·км.
Определите:
1) относительную величину планового задания по росту грузооборота;
2) относительную величину динамики грузооборота;
3) относительную величину выполнения плана по грузообороту.
Поясните взаимосвязь исчисленных показателей. Сделайте выводы.
Задача 3
Имеются следующие данные о работе угольных шахт:
| Номер шахты | I квартал | II квартал | ||
| Добыто угля, тыс. т | Себестоимость 1 т угля, руб. | Затраты на добычу угля, тыс. руб. | Себестоимость 1 т угля, руб. | |
| Шахта 1 | 25 | 3,2 | 90 | 3,0 |
| Шахта 2 | 40 | 2,9 | 135 | 2,7 |
Определитесреднюю себестоимость угля в целом по двум шахтам за каждый квартал.
Задача 4
Имеются следующие данные о товарообороте магазинов области:
| Группа магазинов по объему товарооборота, тыс. руб. | Удельный вес числа магазинов, % |
| До 100 | 2 |
| 100-200 | 8 |
| 200-300 | 12 |
| 300-400 | 30 |
| 400-500 | 23 |
| 500-600 | 15 |
| Свыше 600 | 10 |
| Итого | 100 |
Для характеристики вариации магазинов по объему товарооборота рассчитайте:
1) среднее линейное отклонение;
2) среднее квадратическое отклонение;
3) коэффициент вариации.
Сделайте выводы.
Задача 5
Имеются следующие данные о производстве молока в регионе за 2005-2009 гг., тыс. т:
| 2005 г. | 2006 г. | 2007 г. | 2008 г. | 2009 г. |
| 35,8 | 34,1 | 33,3 | 32,5 | 32,8 |
Определитесреднегодовые абсолютные приросты, среднегодовые темпы роста и прироста производства молока в регионе за 2005-2009 гг.
Задача 6
Жилищный фонд поселка характеризуется следующими данными, тыс. м2:
| Дата | Жилищный фонд |
| На 1 января 2008 г. | 50,2 |
| На 1 апреля 2008 г. | 51,0 |
| На 1 июля 2008 г. | 51,9 |
| На 1 октября 2008 г. | 52,3 |
| На 1 января 2009 г. | 52,8 |
| На 1 июля 2009 г. | 53,9 |
| На 1 ноября 2009 г. | 55,0 |
| На 1 января 2010 г. | 55,8 |
Определите абсолютное и относительное (в процентах) увеличение жилищного фонда в 2009 г. по сравнению с 2008 г.
Задача 7
Имеются следующие данные о продаже товаров в магазине города:
| Вид товара | Стоимость проданных товаров в III квартале, тыс. руб. | Изменение количества проданных товаров в IV квартале по сравнению с III, % |
| Колбасные изделия | 150 | -2 |
| Молочные продукты | 200 | +5 |
| Бакалея | 60 | Без изменения |
Вычислите:
1) общий индекс физического объема товарооборота;
2) общий индекс цен, если известно, что стоимость продаж в IV квартале возросла на 10% по сравнению с III кварталом.
Задача 8
Имеются следующие данные о заработной плате работников трех отделов организации:
| Номер отдела | Июль | Август | ||
| Среднемесячная заработная плата, тыс. руб. | Средняя списочная численность работающих, чел. | Среднемесячная заработная плата, тыс. руб. | Фонд заработной платы, тыс. руб. | |
| 1 | 12 | 35 | 15 | 600 |
| 2 | 25 | 20 | 28 | 396 |
| 3 | 20 | 40 | 25 | 1000 |
Определите:
1) изменение средней заработной платы по каждому отделу организации;
2) изменение средней заработной платы в целом по организации, выделив влияние отдельных факторов (используя индексы переменного, постоянного состава и структурных сдвигов).
Сделайте выводы.
Вариант 4
Задача 1
Имеются следующие данные по торговым предприятиям:
| Номер предприятия | Товарооборот, млн. руб. | Торговая площадь, м2 | Номер предприятия | Товарооборот, млн. руб. | Торговая площадь, м2 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 37 | 270 | 16 | 46 | 333 |
| 2 | 45 | 340 | 17 | 23 | 158 |
| 3 | 33 | 285 | 18 | 76 | 358 |
Окончание таблицы
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 78 | 462 | 19 | 25 | 142 |
| 5 | 59 | 334 | 20 | 88 | 420 |
| 6 | 20 | 236 | 21 | 25 | 248 |
| 7 | 28 | 360 | 22 | 37 | 339 |
| 8 | 75 | 455 | 23 | 19 | 170 |
| 9 | 36 | 314 | 24 | 34 | 340 |
| 10 | 70 | 338 | 25 | 17 | 172 |
| 11 | 40 | 281 | 26 | 34 | 156 |
| 12 | 53 | 304 | 27 | 26 | 144 |
| 13 | 74 | 335 | 28 | 79 | 421 |
| 14 | 60 | 361 | 29 | 74 | 460 |
| 15 | 32 | 312 | 30 | 86 | 452 |
С целью изучения зависимости между размером торговой площади и объемом товарооборота произведите группировку предприятий по размеру торговой площади, выделив четыре группы с равными интервалами; по каждой группе и в целом по совокупности подсчитайте:
а) число предприятий;
б) размер торговой площади - всего и в среднем на одно предприятие;
в) объем товарооборота - всего и в среднем на одно предприятие.
Полученные результаты представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
Имеются следующие данные по фирме, чел.:
| Средняя списочная численность | Базисный год | Отчетный год |
| Рабочих | 210 | 215 |
| Служащих | 90 | 80 |
Определите:
1) относительные величины структуры и координации численности работников за каждый год;
2) относительные величины динамики численности персонала.
Сделайте выводы.
Задача 3
По предприятию имеются данные за два месяца:
| Категория | Апрель | Май | ||
| Средняя заработная плата, руб. | Фонд заработной платы, руб. | Средняя заработная плата, руб. | Численность работников, чел. | |
| Рабочие | 6800 | 9588 | 7000 | 1400 |
| Служащие | 5200 | 1404 | 5800 | 300 |
Определите изменение (в процентах) среднего уровня месячной заработной платы всех работников предприятия в мае по сравнению с апрелем.
Задача 4
Имеются следующие данные о распределении населения региона по величине среднедушевых денежных доходов:
| Среднедушевой денежный доход в месяц, тыс. руб. | Численность населения, % к итогу |
| До 2 | 13,4 |
| 2-4 | 10,8 |
| 4-6 | 24,0 |
| 6-8 | 22,9 |
| 8-10 | 13,7 |
| 10-12 | 8,0 |
| 12 | 7,2 |
| Итого | 100,0 |
Для характеристики дифференциации населения по величине среднедушевых доходов рассчитайте:
1) среднедушевой денежный доход:
2) моду и медиану;
3) децильный коэффициент дифференциации.
Сделайте выводы.
Задача 5
Урожайность озимой пшеницы по району характеризуется следующими данными:
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 |
| Средняя урожайность, ц/га | 23,1 | 22,2 | 24,8 | 24,2 | 23,0 |
Определите:
1) базисные и цепные абсолютные приросты;
2) абсолютное значение 1% прироста;
3) среднюю урожайность за 5 лет;
4) среднегодовые темпы роста и прироста.
Результаты расчетов изложите в табличной форме. Сделайте выводы.
Задача 6
Имеются следующие данные о численности населения района на начало месяца:
| Даты | 1 января | 1 апреля | 1 июля | 1 октября | 1 января следующего года |
| Численность населения, чел. | 34 300 | 34 600 | 34 800 | 34 900 | 35 300 |
Определитесреднегодовую численность населения.
Задача 7
Имеются следующие данные о продаже овощей в магазине города:
| Вид | Май | Июнь | ||
| Продано, т | Товарооборот, тыс. руб. | Продано, т | Товарооборот, тыс. руб. | |
| Капуста | 80,0 | 560,0 | 70,0 | 525,0 |
| Свекла | 50,0 | 400,0 | 45,0 | 450,0 |
| Морковь | 40,0 | 360,0 | 30,0 | 330,0 |
Определите:
1) общие индексы физического объема продаж, цен и стоимости товарооборота в фактических ценах, покажите их взаимосвязь;
2) абсолютное изменение товарооборота - общее, в том числе за счет изменения цен и физического объема продаж.
Задача 8
Имеются следующие данные о выпуске кирпича тремя предприятиями фирмы:
| Номер | Выпуск, тыс. шт. | Себестоимость 1000 шт., руб. | ||
| Сентябрь | Октябрь | Сентябрь | Октябрь | |
| 1 | 30 | 35 | 610 | 608 |
| 2 | 60 | 77 | 590 | 580 |
| 3 | 30 | 28 | 630 | 628 |
Определите:
1) изменение себестоимости по каждому предприятию фирмы;
2) изменение средней себестоимости в целом по фирме, выделив влияние отдельных факторов (используя индексы переменного, постоянного состава и структурных сдвигов).
Вариант 5
Задача 1
Имеются следующие данные по совокупности предприятий:
| Номер предприятия | Среднегодовая стоимость основных фондов, млн. руб. | Объем продукции, млн. руб. | Номер предприятия | Среднегодовая стоимость основных фондов, млн. руб. | Объем продукции, млн. руб. |
| 1 | 25,4 | 33,2 | 16 | 7,2 | 7,2 |
| 2 | 13,8 | 15,2 | 17 | 8,8 | 13,4 |
| 3 | 14,6 | 22,4 | 18 | 13,8 | 16,8 |
| 4 | 5,8 | 6,4 | 19 | 9,2 | 13,8 |
| 5 | 9,0 | 9,8 | 20 | 11,6 | 13,4 |
| 6 | 25,6 | 30,0 | 21 | 23,4 | 35,8 |
| 7 | 15,6 | 24,0 | 22 | 14,8 | 20,8 |
| 8 | 1,6 | 1,4 | 23 | 21,8 | 31,0 |
| 9 | 8,2 | 10,6 | 24 | 5,4 | 7,8 |
| 10 | 8,6 | 9,6 | 25 | 9,6 | 11,9 |
| 11 | 11,0 | 11,4 | 26 | 2,4 | 3,8 |
| 12 | 8,6 | 9,6 | 27 | 23,8 | 32,5 |
| 13 | 18,2 | 21,8 | 28 | 9,4 | 11,5 |
| 14 | 2,8 | 2,4 | 29 | 15,2 | 19,8 |
| 15 | 15,2 | 17,2 | 30 | 15,6 | 20,2 |
С целью изучения зависимости между среднегодовой стоимостью основных фондов и объемом продукции произведите группировку предприятий по стоимости основных фондов, выделив четыре группы с равными интервалами; по каждой группе и в целом подсчитайте:
а) число предприятий;
б) среднегодовую стоимость основных фондов - всего и в среднем на одно предприятие;
в) стоимость продукции - всего и в среднем на одно предприятие;
г) объем продукции в расчете на 1 руб. основных фондов (фондоотдачу).
Полученные результаты представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
Известны объемы производства отдельных видов промышленной продукции в трех странах за год.
| Вид продукции | Страна-производитель | ||
| Великобритания | Германия | Россия | |
| Электроэнергия, млрд. кВт·ч | 396 | 617 | 953 |
| Нефть, млн. т | 87,5 | 3,5 | 470 |
Вычислитеотносительные показатели уровня экономического развития, используя следующие данные о среднегодовой численности населения, млн. чел.: Великобритания - 10,1; Германия - 82,5; Россия - 143,8. Определите виды рассчитанных относительных величин.
Задача 3
Имеются следующие данные о реализации товара "А" на рынках города:
| Рынок | Апрель | Май | ||
| Цена за 1 кг, руб. | Продано, т | Цена за 1 кг, руб. | Реализовано на сумму, тыс. руб. | |
| 1 | 8,5 | 44 | 9,5 | 408,5 |
| 2 | 7,5 | 47 | 8,0 | 360,0 |
| 3 | 7,0 | 45 | 7,5 | 315,0 |
Определитесреднюю цену данного товара за каждый месяц.
Задача 4
Для изучения норм выработки на заводе проведено обследование затрат времени рабочих-станочников. Получено распределение рабочих по затратам времени на обработку одной детали, мин.:
| Затраты времени на одну деталь | Число рабочих, % к итогу |
| До 24 | 12,0 |
| 24-26 | 13,1 |
| 26-28 | 22,8 |
| 28-30 | 16,7 |
| 30-32 | 16,2 |
| 32-34 | 13,9 |
| 34-36 | 5,3 |
| Итого | 100,0 |
Определите:
1) средние затраты времени на одну деталь;
2) моду и медиану;
3) коэффициент вариации.
Сделайте выводы.
Задача 5
Имеются данные о потреблении хлебных продуктов в домашних хозяйствах региона (в среднем на члена домохозяйства в год):
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 |
| Хлебные продукты, кг | 104 | 107 | 101 | 97 | 103 |
| Фрукты и ягоды, кг | 68 | 64 | 66 | 70 | 77 |
Определитедля каждого ряда динамики:
1) средний уровень;
2) цепные и базисные абсолютные приросты;
3) цепные и базисные темпы роста.
Задача 6
Автотранспортное предприятие по состоянию на 1 января 2009 г. имело 200 автомашин, 1 апреля выбыло 5 автомашин, 1 сентября в распоряжение автотранспортного предприятия поступило 15 автомашин.
Вычислите среднегодовую численность автомашин предприятия.
Задача 7
Имеются следующие данные о продаже товаров:
| Товарная | Продано товаров, тыс. руб. | Индексы количества проданных товаров в отчетном периоде по сравнению с базисным | |
| Базисный период | Отчетный период | ||
| Ткани шерстяные | 4200 | 4000 | 0,98 |
| Трикотажные изделия | 5200 | 5300 | 1,05 |
| Обувь | 3200 | 4500 | 1,20 |
Вычислите общий индекс физического объема товарооборота в отчетном периоде по сравнению с базисным.
Используя взаимосвязи индексов, определите, на сколько процентов в среднем изменились цены на проданные товары.
Сделайте выводы.
Задача 8
Имеются следующие данные о реализации картофеля на рынках города:
| Рынок | Март | Апрель | ||
| Цена, руб./кг | Продано, т | Цена, руб./кг | Товарооборот, тыс. руб. | |
| 1 | 25 | 10 | 30 | 360 |
| 2 | 40 | 8 | 35 | 280 |
Определите:
1) изменение цен на картофель на каждом рынке города;
2) изменение в структуре продаж картофеля в апреле по сравнению с мартом;
3) изменение средней цены реализации 1 кг картофеля (индекс цен переменного состава);
4) индекс цен постоянного состава;
5) индекс влияния структурных сдвигов.
Вариант 6
Задача 1
Имеются следующие данные по совокупности предприятий:
| Номер предприятия | Среднесписочная численность работников, чел. | Объем продукции, млн. руб. | Номер предприятия | Среднесписочная численность работников, чел. | Объем продукции, млн. руб. |
| 1 | 362 | 3,2 | 16 | 400 | 6,9 |
| 2 | 380 | 6,6 | 17 | 310 | 3,6 |
| 3 | 220 | 1,5 | 18 | 450 | 8,0 |
| 4 | 460 | 4,2 | 19 | 300 | 2,5 |
| 5 | 393 | 6,4 | 20 | 350 | 2,8 |
| 6 | 282 | 2,8 | 21 | 258 | 2,5 |
| 7 | 580 | 9,4 | 22 | 329 | 1,6 |
| 8 | 200 | 1,9 | 23 | 435 | 5,6 |
| 9 | 270 | 2,5 | 24 | 505 | 4,4 |
| 10 | 338 | 3,5 | 25 | 372 | 4,1 |
| 11 | 200 | 2,3 | 26 | 592 | 8,2 |
| 12 | 250 | 1,3 | 27 | 408 | 4,2 |
| 13 | 310 | 1,4 | 28 | 481 | 7,3 |
| 14 | 410 | 3,0 | 29 | 464 | 5,6 |
| 15 | 600 | 2,5 | 30 | 540 | 4,7 |
С целью изучения зависимости между численностью работников и объемом продукции произведите группировку предприятий по численности работников, выделив пять групп с равными интервалами; по каждой группе и в целом по совокупности подсчитайте:
а) число предприятий;
б) среднесписочную численность работников - всего и в среднем на одно предприятие;
в) объем продукции - всего и в среднем на одно предприятие.
Полученные результаты представьте в виде групповой таблицы. Сделайте выводы.
Задача 2
Имеются данные о среднемесячной номинальной начисленной заработной плате работников организаций по видам экономической деятельности в регионе, руб.
| Вид деятельности | 2005 г. | 2008 г. |
| Сельское хозяйство, охота и лесное хозяйство | 866 | 2785 |
| Добыча полезных ископаемых | 3975 | 17 142 |
| Здравоохранение и предоставление социальных услуг | 1228 | 5101 |
| Обрабатывающие производства | 2942 | 9183 |
| Образование | 1131 | 4895 |
Определите:
1) относительные величины динамики;
2) относительные величины сравнения.
Сделайте выводы.
Задача 3
Выпуск продукции двумя предприятиями АО характеризуется следующими данными:
| Номер предприятия | I квартал | II квартал | ||
| Стоимость продукции I сорта, тыс. р. | Удельный вес продукции I сорта, % | Стоимость всей произведенной продукции тыс. руб. | Удельный вес продукции I сорта, % | |
| 1 | 130 | 92 | 153 | 95 |
| 2 | 68 | 80 | 65 | 82 |
Определите в целом по АО средний удельный вес продукции I сорта в каждом квартале.
Задача 4
Имеются следующие данные о распределении рабочих по стажу
работы, лет:
| Группы рабочих по стажу работы | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25 и более | Итого |
| Число рабочих, чел. | 20 | 30 | 40 | 50 | 40 | 20 | 200 |
Определите:
1) средний стаж работы рабочих;
2) среднее квадратическое отклонение;
3) коэффициент вариации.
Сделайте выводы.
Задача 5
Обеспеченность населения региона легковыми автомобилями в личной собственности на конец года в расчете на 1000 чел. за период
с 2005 по 2009 г. характеризуется следующими данными:
| Годы | 2005 | 2006 | 2007 | 2008 | 2009 |
| Количество легковых автомобилей, шт. | 96 | 110 | 122 | 143 | 156 |
Определите:
1) средний уровень ряда динамики;
2) цепные и базисные темпы прироста;
3) абсолютное значение 1% прироста для каждого года;
4) средние обобщающие показатели ряда динамики.
Сделайте выводы.
Задача 6
Имеются данные о численности специалистов с высшим и специальным средним образованием (человек) двух регионов:
| Дата | І регион | ІІ регион |
| 1 января 2009 г. | 1850 | 1720 |
| 1 апреля 2009 г. | 1866 | 1810 |
| 1 декабря 2009 г. | 1910 | 1860 |
| 1 января 2010 г. | 1960 | 1900 |
Определите:
1) среднегодовую численность специалистов по каждому региону;
2) сопоставьте (в абсолютном и относительном выражении) среднюю численность специалистов в регионах.
Задача 7
Имеются следующие данные по машиностроительному заводу:
| Изделие | Реализовано продукции в отчетном периоде, тыс. руб. | Изменение цен в отчетном периоде по сравнению с базисным, % |
| А | 2300 | +7,0 |
| Б | 2100 | Без изменения |
| В | 2900 | -2,0 |
Вычислитеобщий индекс цен и физического объема продукции, если известно, что стоимость реализованной продукции в фактических ценах возросла на 15%. Сделайте выводы.
Задача 8
Имеются следующие данные о выпуске продукции "А" и ее себестоимости по двум заводам:
| Номер завода | Январь | Февраль | ||
| Произведено продукции, тыс. шт. | Себестоимость единицы, руб. | Произведено продукции, тыс. шт. | Себестоимость единицы, руб. | |
| 1 | 60 | 24 | 80 | 20 |
| 2 | 60 | 20 | 120 | 18 |
Вычислите:
1) индекс себестоимости переменного состава;
2) индекс себестоимости постоянного (фиксированного) состава;
3) индекс влияния структурных сдвигов.
Сделайте выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО КУРСУ
1. Предмет, методы и задачи статистики. Основные категории статистической науки.
2. Понятие статистического наблюдения, его организационные формы и виды.
3. Программно-методологические и организационные вопросы статистического наблюдения.
4. Метод статистических группировок и его значение. Типологические, структурные, аналитические группировки.
5. Статистические таблицы, их виды, правила построения.
6. Обобщающие статистические показатели. Виды абсолютных и относительных величин в статистике.
7. Сущность и значение средних величин; виды средних и методы их расчета.
8. Показатели вариации.
9. Показатели структурных различий.
10. Ряды динамики: понятие, виды рядов динамики, обеспечение сопоставимости в рядах динамики.
11. Аналитические показатели динамики.
12. Средние характеристики рядов динамики.
13. Основная тенденция развития в рядах динамики и методы ее выявления.
14. Статистические индексы. Индивидуальные и общие индексы. Агрегатный индекс как основная форма общего индекса.
15. Средние индексы.
16. Индексный метод анализа динамики среднего уровня.
17. Экономические индексы и их взаимосвязи.
18. Статистические методы изучения взаимосвязей экономических и социальных явлений.
19. Основные условия и принципы применения корреляционно-регрессионного анализа статистических связей.
20. Графический метод в статистике.
ПРИМЕРНЫЕ ТЕСТЫ К ЭКЗАМЕНУ (ЗАЧЕТУ)
1.В чем отличие статистики от других общественных наук?
а) статистика изучает взаимосвязи явлений;
б) статистика обеспечивает количественно-качественную характеристику общественных явлений в конкретных условиях места и времени;
в) статистика изучает объективно складывающиеся отношения в процессе производства распределения обмена и потребления жизненных благ;
г) статистика изучает логические понятия, отражающие общие и существенные стороны экономической жизни общества.
2.Объектом исследования статистики является:
а) изучаемое явление (процесс);
б) статистическая совокупность как набор элементарных единиц;
в) окружающая среда, в которой находится элементарная единица;
г) статистические показатели.
3.Предметом исследования статистики являются:
а) статистические закономерности;
б) массовые явления и процессы общественной жизни;
в) взаимосвязи явлений и процессов;
г) статистические показатели.
4.Статистическая совокупность - это:
а) множество единиц; в) группа элементов;
б) массовое общественное явление; г) источник информации.
5.Единица статистической совокупности - это:
а) один из элементов статистической совокупности;
б) отчетная единица;
в) отдельный человек;
г) источник информации.
6.Статистическая методология - это:
а) статистические методы изучения;
б) категории и понятия статистики;
в) методы изучения динамики явлений;
г) статистические показатели.
7.Общим принципом, лежащим в основе исследования статистических закономерностей, выступает:
а) закон стоимости;
б) закон сохранения массы вещества;
в) закон спроса и предложения;
г) закон больших чисел.
8.Признак в статистике - это:
а) суммарные показатели;
б) числовые выражения единиц совокупности;
в) свойство изучаемой единицы статистической совокупности;
г) показатели структуры совокупности.
9.Признаки в статистике по характеру выражения подразделяются:
а) на моментные и интервальные;
б) на дискретные и непрерывные;
в) на прямые и косвенные;
г) на качественные и количественные.
10.К атрибутивным признакам относят:
а) пол человека; в) посевная площадь;
б) численность населения страны; г) национальность.
11.Количественные признаки группировок:
а) место жительства; в) прибыль предприятия;
б) национальность; г) возраст человека.
12.Дискретные признаки группировок:
а) число членов семей; в) заработная плата рабочих;
б) разряд сложности работы; г) пол человека.
13.Непрерывные признаки группировок:
а) разряд сложности работы; в) заработная плата работающих;
б) прибыль предприятия; г) национальность.
14.Статистический метод включает:
а) организационный план, переписной лист и статистический инструментарий;
б) статистическое наблюдение, сводку и группировку, расчет обобщающих показателей;
в) изучение структуры, динамики и взаимосвязей явлений;
г) информационное познание объекта и выявление количественных закономерностей.
15.Задачей статистического наблюдения является:
а) первичная обработка и сводка данных;
б) расчет обобщающих показателей;
в) сбор массовых данных об изучаемых явлениях;
г) выявление количественных закономерностей.
16.К формам статистического наблюдения относятся:
а) регистры;
б) непосредственное наблюдение;
в) опрос;
г) статистическая отчетность.
17. К видам статистического наблюдения по охвату единиц совокупности относят:
а) документальное; в) сплошное;
б) выборочное; г) текущее.
18. К видам несплошного статистического наблюдения относят:
а) монографическое;
б) обследование основного массива;
в) выборочное наблюдение;
г) текущее статистическое наблюдение.
19. К видам статистического наблюдения по характеру регистрации фактов во времени относят:
а) единовременное; в) сплошное;
б) текущее; г) монографическое.
20. Метод основного массива - это:
а) вид статистического наблюдения;
б) форма статистического наблюдения;
в) способ статистического наблюдения;
г) метод изучения динамики явления.
21. Выборочным называется такое статистическое наблюдение, при котором обследуется:
а) научно отобранная часть совокупности;
б) вся совокупность;
в) любая часть совокупности;
г) разные части совокупности.
22. Перечень вопросов (или признаков), подлежащих регистрации в процессе наблюдения, называют:
а) отчетность; в) программа наблюдения;
б) статистический формуляр; г) регистр.
23. Расхождение между расчетными значениями и действительными значениями изучаемых величин называется:
а) ошибка наблюдения; в) ошибка регистрации;
б) ошибка репрезентативности; г) вариация признака.
24. Расхождение между расчетными значениями признака в выборочной совокупности и действительными значениями признака в генеральной совокупности - это:
а) ошибка регистрации; в) ошибка репрезентативности;
б) ошибка наблюдения; г) ошибка метода расчета.
25. При непрерывной вариации признака строится:
а) дискретный вариационный ряд;
б) атрибутивный ряд;
в) интервальный вариационный ряд;
г) временной ряд.
26. Графическое изображение интервального ряда называется:
а) полигон; б) кумулята; в) гистограмма; г) огива.
27. Дискретный вариационный ряд графически изображается с помощью:
а) полигона; б) кумуляты; в) гистограммы; г) функции.
28. Население, проживающее на данной территории, распределяют на группы по национальному признаку. Полученный ряд называется:
а) вариационным; в) атрибутивным;
б) дискретным; г) интервальным.
29. Группировку, выявляющую взаимосвязи между изучаемыми явлениями и их признаками, называют:
а) рядом распределения; в) аналитической группировкой;
б) типологической группировкой; г) структурной группировкой.
30. Группировка, характеризующая состав совокупности, называется:
а) типологической; в) аналитической;
б) структурной; г) альтернативной.
31. Студенты, обучающиеся без отрыва от производства, подразделяются на студентов вечерней, заочной форм обучения и обучающихся по системе дистанционного обучения. Данная группировка является:
а) типологической; в) структурной;
б) аналитической; г) вторичной.
32. Максимальное и минимальное значения признаков в совокупности равны, соответственно, 28 и 4. Определите величину интервала группировки, если выделяется шесть групп:
а) 5,3; б) 5,5; в) 4,0; г) 7,0.
33. Статистическая таблица, в подлежащем которой содержится группировка единиц по одному количественному или атрибутивному признаку, называется:
а) простой; в) групповой;
б) перечневой; г) комбинационной.
34. Сказуемое статистической таблицы - это:
а) значения строк;
б) показатели, характеризующие изучаемый объект;
в) суммарные показатели;
г) числовые выражения единиц совокупности.
35. Укажите вид таблицы, в которой оформляется ряд динамики:
а) простая территориальная; в) простая хронологическая;
б) простая перечневая; г) групповая.
36. Обобщенную количественную характеристику свойств изучаемого явления или процесса в условиях конкретного места и времени называют:
а) статистическим показателем;
б) статистическими данными;
в) статистической совокупностью;
г) статистическим признаком.
37. Абсолютные величины могут выражаться:
а) в натуральных единицах измерения;
б) в виде простого кратного отношения;
в) в денежных единицах измерения;
г) в трудовых единицах измерения.
38. Для преобразования натуральных единиц измерения в условно-натуральные необходимо воспользоваться:
а) коэффициентами опережения;
б) коэффициентами перевода;
в) коэффициентами замедления;
г) коэффициентами роста.
39. Относительные статистические величины могут выражаться:
а) в натуральных единицах измерения;
б) в процентах;
в) в денежных единицах измерения;
г) в виде простого кратного отношения.
40. Отношение одноименных абсолютных показателей, соответствующих одному и тому же периоду или моменту времени, относящихся к различным совокупностям, называются относительными величинами:
а) планового задания; в) интенсивности;
б) динамики; г) сравнения.
41. Разделив численность населения Самарской области на численность населения Ульяновской области, можно получить относительную величину:
а) координации; в) сравнения;
б) интенсивности; г) динамики.
42. Сопоставляя одноименные величины, относящиеся к разным периодам времени, получают относительные величины:
а) динамики; в) интенсивности;
б) наглядности; г) структуры.
43. Взаимосвязь относительных величин динамики (ОВД), планового задания (ОВПЗ) и выполнения плана (ОВВП) выражается соотношением:
а) ОВД = ОВПЗ · ОВВП; в) ОВПЗ = ОВД · ОВВП;
б) ОВД = ОВПЗ / ОВВП; г) ОВВП = ОВД · ОВПЗ.
44. По отделению дороги планом предусмотрено увеличение объема отправок груза на 10,0%. Фактически объем отправок против прошлого года повысился на 12,2%. Процент перевыполнения плана по объему отправок груза составил (с точностью до 0,1%):
а) 2,0; б) 2,2; в) 1,2; г) 10,2.
45. По плану фирмы предусматривалось снижение себестоимости за период на 2%, фактически себестоимость возросла на 2%. На сколько процентов (с точностью до 0,1) фактическая себестоимость отличается от плановой:
а) 4,1; б) 5,6; в) 3,9; г) 0,25.
46. Планом на 2009 г. предусмотрен рост товарооборота магазина на 5%. Фактически в отчетном периоде он увеличился на 8% по сравнению с 2008 г. Относительный показатель выполнения плана товарооборота (с точностью до 0,1%):
а) 102,9; б) 113,4; в) 97,2; г) 103,0.
47. В I квартале товарооборот магазина составил 300 млн. руб., а во II квартале - 400 млн. руб. при плане 360 млн. руб. Относительный показатель выполнения плана товарооборота магазином во II квартале:
а) 120,0%; б) 133,3%; в) 111,1%; г) 83,3%.
48. В I квартале товарооборот магазина составил 300 млн. руб., а во II квартале - 400 млн. руб. при плане 360 млн. руб. Относительный показатель планового задания:
а) 120,0%; б) 133,3%; в) 111,1%; г) 83,3%.
49. Плановый прирост выпуска продукции в текущем году по отраслям должен был составить 6,7%. Если фактический прирост выпуска продукции по сравнению с базисным годом составил 9,2%, то степень выполнения плана (с точностью до 0,1%) равна:
а) 101,8; б) 102,3; в) 103,4; г) 102,5.
50. В 2008 г. предприятие увеличило выпуск продукции по сравнению с 2007 г. на 10%, а в 2009 г. выпуск продукции на предприятии по сравнению с 2007 г. снизился на 5%.
Выпуск продукции в 2009 г. по сравнению с 2007 г. составил, %
(с точностью до 0,1%):
а) 104,5; б) 105,6; в) 98,3; г) 99,2.
51. Имеются следующие данные о численности постоянного населения региона по состоянию на начало 2010 г. (тыс. чел.): все население - 1298,9, в том числе мужчин - 600,2, женщин - 698,7. Относительная величина координации, т.е. число мужчин, приходящееся на 1000 женщин области, будет равна:
а) 859; б) 538; в) 462; г) 1164.
52.Средняя величина может быть вычислена:
а) для количественного признака;
б) для альтернативного признака;
в) для атрибутивного признака;
г) для одинакового по величине уровня признака у разных единиц совокупности.
53. Сумма отклонений индивидуальных значений признака от их средней величины:
а) больше нуля; в) равна нулю;
б) меньше нуля; г) больше или равна нулю.
54. При расчете средней величины вес каждой варианты уменьшен в 3 раза. В этом случае средняя величина:
а) не изменится; в) увеличится в 3 раза;
б) уменьшится в 3 раза; г) уменьшится в 9 раз.
55. Каждая варианта увеличена в 10 раз. Средняя величина в этом случае:
а) не изменится; в) увеличится в 10 раз;
б) уменьшится в 10 раз; г) увеличится на 100 ед.
56. Если вычислять средние по одному и тому же набору исходных данных, то наибольший результат получим при использовании:
а) средней арифметической; в) средней гармонической;
б) средней квадратической; г) средней геометрической.
57. Если веса осредняемого признака выражены в процентах, знаменатель при расчете средней арифметической будет равен:
а) 1000; б) 100; в) 10; г) 1.
58. Средняя арифметическая взвешенная имеет вид:
а)  б)
б)  в)
в)  г)
г) 
59. Средняя арифметическая имеет вид:
а)  б)
б)  в)
в)  ; г)
; г) 
60. Средняя гармоническая простая имеет вид:
а)  б)
б)  в)
в)  г)
г) 
61. Средняя гармоническая взвешенная имеет вид:
а)  б)
б)  в)
в)  г)
г) 
62. Выбор вида средней зависит:
а) от характера исходных данных;
б) от единиц измерения показателя;
в) от степени вариации признака;
г) от общего объема признака.
63.Средняя гармоническая вычисляется, когда в качестве веса известны:
а) объемные значения признака;
б) численность единиц;
в) удельные веса объемных значений признака;
г) удельные веса численности единиц;
64. Количественный признак принимает всего два значения: 10 и 20. Часть первого из них равна 30%. Среднее значение признака равно:
а) 15,0; б) 37,5; в) 17,0; г) 18,5.
65. Предприятие получает сырье от трех поставщиков по ценам 200, 250, 300 руб./т в количестве 41, 42, 43 т, соответственно. Средняя цена за 1 т сырья равна:
а) 244,2; б) 253,2; в) 250,8; г) 250,0.
66. Имеются следующие данные о продажах картофеля на рынках:
| Номер рынка | Цена на картофель руб./кг | Выручка от продажи, тыс. руб. |
| 1 | 4 | 160 |
| 2 | 5 | 100 |
| 3 | 6 | 60 |
Средняя по трем рынкам цена картофеля будет находиться в интервале, руб.:
а) до 4,5; б) 4,5-5,0; в) 5,0-5,5; г) 5,5 и более.
67. На фирме упаковкой и отправкой заказа занимаются двое рабочих. Первый рабочий тратит на обработку заказа 10 мин, второй - 14 мин. Среднее время на обработку одного заказа будет находиться в интервале:
а) до 11,0; б) 11,0-11,5; в) 11,5-12,0; г) 12,0 и более.
68. Имеется ряд распределения:
| Тарифный разряд рабочих | 2 | 3 | 4 | 5 | 6 |
| Число рабочих | 8 | 16 | 17 | 12 | 7 |
Средний тарифный разряд рабочих равен (с точностью до 0,1):
а) 4,2; б) 3,7; в) 3,9; г) 4,8.
69. Если данные о заработной плате рабочих представлены интервальным рядом распределения, то за основу расчета среднего заработка следует принимать:
а) начало интервалов;
б) середины интервалов;
в) конец интервалов;
г) средние значения заработной платы в интервале.
70. Данные о торгах на фондовой бирже:
| Номер сделки | Курс продажи, руб. | Количество проданных акций, шт. |
| 1 | 108 | 500 |
| 2 | 10 | 300 |
| 3 | 1000 | 10 |
Средний курс продажи акций (с точностью до целых) равен:
а) 270; б) 83; в) 95; г) 383.
71. Реализация продукции одного вида на трех предприятиях за период характеризуется следующими данными:
| Номер предприятия | Объем реализации, тыс. руб. | Средняя цена за единицу, руб. |
| 1 | 20 000 | 1600 |
| 2 | 20 160 | 1680 |
| 3 | 19 926 | 1620 |
Средняя цена единицы продукции по совокупности предприятий равна:
а) 1632,8; б) 1680,0; в) 1633,3; г) 1633,5.
72. К показателям структуры вариационного ряда относятся:
а) дисперсия; в) медиана;
б) мода; г) коэффициент вариации.
73. Модой называется:
а) среднее значение признака в данном ряду распределения;
б) наиболее часто встречающееся значение признака в данном ряду;
в) серединное значение признака в данном ряду распределения;
г) значение признака, делящее совокупность на две равные части.
74. Для значений признака: 3, 3, 3, 4, 4, 6, 7, 9, 9. Мода:
а) равна 6; б) равна 4; в) отсутствует; г) равна 3.
75. Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:
| Товарооборот, млн. руб. | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25 и более | Итого |
| Число фирм | 20 | 26 | 20 | 14 | 10 | 10 | 100 |
Мода (с точностью до 0,1) равна:
а) 7,5; б) 8,9; в) 10,5; г) 9,0.
76. Результат экзамена по статистике:
| Бал оценки знаний студентов | 2 (неудовле- творительно) | 3 (удовле- творительно) | 4 (хорошо) | 5 (отлично) |
| Число студентов | 9 | 12 | 24 | 15 |
Медиана равна:
а) 3; б) 5; в) 4; г) 2.
77. В результате выборочного обследования счетов вкладчиков коммерческого банка получен следующий ряд распределения:
| Размер вклада, тыс. руб. | До 40 | 40-60 | 60-80 | 80-100 | 100 и более | Итого |
| Число вкладов | 2 | 10 | 15 | 17 | 6 | 50 |
Медиана (с точностью до 0,1) равна:
а) 77,3; б) 78,0; в) 82,1; г) 89,2.
78. Имеется ряд распределения:
| Тарифный разряд | 2 | 3 | 4 | 5 | 6 |
| Число рабочих | 8 | 16 | 17 | 12 | 7 |
Медиана равна (с точностью до 0,1):
а) 3; б) 4,5; в) 4; г) 3,5.
79. Коэффициент децильной дифференциации рассчитывается по формуле:
а) КД = Д9/Д1; б) КД = Д1/Д9; в) КД = Д10/Д9; г) КД = Д10/Д1.
80. Вариация - это:
а) изменяемость величины признака у отдельных единиц совокупности;
б) изменение структуры совокупности во времени;
в) изменение состава совокупности;
г) изменение структуры совокупности в пространстве.
81. Как характеризует совокупность и среднюю арифметическую величину, равную 17, коэффициент вариации, равный 24,1%:
а) совокупность однородна, а средняя типична;
б) совокупность разнородна, а средняя типична;
в) совокупность однородна, а средняя не является типичной величиной;
г) совокупность разнородна, а средняя не является типичной величиной.
82. Формула для расчета дисперсии признака по сгруппированным данным:
а)  ; б)
; б)  в)
в)  г)
г)  .
.
83. Размах вариации - это:
а)  в)
в) 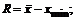
б)  г)
г) 
84. Численность тридцатилетних составляет 160 чел., а двадцати- и сорокалетних - по 20 чел. Размах вариации равен:
а) 40; б) 140; в) 20; г) 120.
85. Если условную совокупность составляют лица в возрасте 20, 30 и 40 лет, то каким показателем можно оценить величину вариации признака?
а) размахом вариации;
б) средним квадратическим отклонением;
в) средним линейным отклонением;
г) коэффициентом вариации.
86. Какой из показателей вариации характеризует абсолютный размер колеблемости признака около средней величины?
а) коэффициент осцилляции;
б) среднее квадратическое отклонение;
в) размах вариации;
г) индекс Рябцева.
87. Коэффициент вариации характеризует:
а) степень вариации признака;
б) типичность средней;
в) тесноту связей между признаками;
г) пределы колеблемости признака.
88. Средняя величина признака равна 22, дисперсия признака - 36. Коэффициент вариации (с точностью до 0,1%) равен:
а) 32,7; б) 27,3; в) 63,6; г) 40,2.
89. В студенческой группе из 25 человек трое имеют задолженности по результатам зимней сессии. Дисперсия успеваемости равна:
а) 0,0475; б) 0,1056; в) 0,090; г) 0,1065.
90. Признак совокупности принимает два значения: 10 и 20. Частость первого из них 30%, второго - 70%. Среднее квадратическое отклонение равно 4,1. Коэффициент вариации (с точностью 0,1%) равен:
а) 27,3; б) 24,1; в) 32,8; г) 35,7.
91. Недостающим элементом в формуле среднего квадратического отклонения является 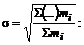
а)  б)
б)  в)
в)  г)
г) 
92. Величина дисперсии альтернативного признака находится в интервале:
а) 0,0-0,25; б) 0,0-0,50; в) 0,0-1,0; г) 0,25-0,50.
93. Численность тридцатилетних составляет 160 чел., а двадцати- и сорокалетних - по 20 чел. Средний возраст - 30 лет. Среднее квадратическое отклонение будет по своей величине (с точностью до 0,1):
а) менее 4,4; в) более 4,4;
б) равно 4,4; г) рассчитать невозможно.
94. Ряд динамики состоит:
а) из вариантов значения признака; в) из показателей времени;
б) из частот; г) из уровней.
95. Вид ряда динамики, уровни которого характеризуют добычу нефти по региону за каждый год периода 2002-2009 гг., т:
а) интервальный;
б) моментный с равными интервалами;
в) производный;
г) моментный с неравными интервалами.
96. Данные на начало месяца, млн. руб.:
на 1 апреля 2009 г. - 300 на 1 июня 2009 г. - 310
на 1 мая 2009 г. - 320 на 1 июля 2009 г. - 290
Для расчета среднего остатка оборотных средств за II квартал следует применить:
а) среднюю гармоническую; в) среднюю геометрическую;
б) среднюю хронологическую; г) среднюю арифметическую.
97. Средний уровень моментного ряда динамики с неравными временными промежутками исчисляется по формуле средней:
а) арифметической простой;
б) арифметической взвешенной;
в) гармонической простой;
г) хронологической взвешенной.
98. Имеются данные о численности специалистов с высшим и специальным средним образованием по региону, чел:
| Дата | Численность специалистов |
| 1 января 2009 г. | 1850 |
| 1 апреля 2009 г. | 1866 |
| 1 октября 2009 г. | 1910 |
| 1 января 2010 г. | 1960 |
Среднегодовая численность специалистов по региону за 2009 г. составит:
а) 1897; б) 1892; в) 1893; г) 1900.
99. Базисный абсолютный прирост определяется по формуле:
а)  в)
в) 
б)  г)
г) 
100. Цепной абсолютный прирост определяется по формуле:
а)  в)
в) 
б)  г)
г) 
101. Базисный абсолютный прирост конечного уровня определяется как:
а) отношение конечного уровня к начальному;
б) сумма цепных абсолютных приростов;
в) произведение цепных темпов роста;
г) отношение текущего уровня к предыдущему.
102. Цена на товар "А" выросла в феврале по сравнению с январем на 2 руб., в марте по сравнению февралем еще на 2 руб., а в апреле по сравнению с мартом на 3 руб.
На сколько рублей выросла цена в апреле по сравнению с январем:
а) 7; б) 10; в) 12; г) 14.
103. По формуле 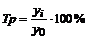 определяется:
определяется:
а) цепной темп роста; в) цепной темп прироста;
б) базисный темп роста; г) базисный темп прироста.
104. Среднее абсолютное содержание одного процента прироста равно 18 ед., средний темп роста - 102,5%. Средний абсолютный прирост равен (с точностью до 0,1):
а) 18,5; б) 45,0; в) 20,4; г) 17,6.
105. Для расчета среднего темпа роста используют:
а) среднюю арифметическую;
б) среднюю геометрическую;
в) среднюю хронологическую;
г) среднюю гармоническую.
106. В феврале объем продаж по сравнению с январем удвоился, в марте остался таким же, как в феврале, а в апреле по сравнению с мартом вырос в 4 раза. Среднемесячный темп прироста за февраль - апрель равен (с точностью до целых):
а) 120%; б) 100%; в) 166%; г) 200%.
107. Что характеризует общая тенденция ряда динамики:
а) периодические внутригодовые изменения уровней ряда;
б) общую закономерность изменения явления во времени;
в) изменение в распределении единиц изучаемой совокупности;
г) колеблемость уровней ряда.
108. Экстраполяция рядов динамики - это:
а) определение величины промежуточных уровней ряда динамики;
б) определение величины уровней ряда за его пределами;
в) расчет параметров уравнения общей тенденции развития;
г) определение величины колеблемости уровней ряда динамики.
109. Интерполяция рядов динамики - это:
а) определение величины промежуточных уровней ряда динамики;
б) определение величины уровней ряда за его пределами;
в) расчет параметров уравнения общей тенденции развития;
г) определение величины колеблемости уровней ряда динамики.
110. Методом аналитического выравнивания по прямой выявлена тенденция ряда динамики:
 = 917,2 + 59,2t.
= 917,2 + 59,2t.
| Год | Объем выручки (у), тыс. руб. | t |
| 2005 | 800 | -2 |
| 2006 | 857 | -1 |
| 2007 | 915 | 0 |
| 2008 | 976 | 1 |
| 2009 | 1038 | 2 |
Теоретическое значение показателя объема выручки в 2011 г. составит:
а) 1154; б) 739; в) 1245; г) 917.
111. Индекс исчисляется как:
а) отношение одной величины к другой;
б) сумма величин;
в) разность между двумя величинами;
г) произведение величин.
112.Индивидуальные индексы характеризуют изменение:
а) отдельного элемента явления;
б) изучаемой совокупности в целом;
в) группы элементов;
г) среднего уровня статистического показателя.
113. Если индивидуальный индекс цен  то это означает, что цена на товар:
то это означает, что цена на товар:
а) составила 98 ед.; в) снизилась на 0,98;
б) снизилась на 2%; г) снизилась на 98%.
114. Общий индекс физического объема товарооборота в агрегатной форме имеет вид:
а)  б)
б)  в)
в) 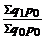 ; г)
; г)  .
.
115. При расчете индекс товарооборота получился равным 1,25. Это означает, что:
а) товарооборот в отчетном периоде по сравнению с базисным увеличился в 1,25 раза;
б) товарооборот стал меньше на 25%;
в) товарооборот увеличился на 125%;
г) в отчетном периоде товарооборот составил 1,25% от базисного.
116. Средние индексы исчисляются как средняя величина из индексов:
а) индивидуальных; в) базисных агрегатных;
б) цепных агрегатных; г) Пааше и Ласпейреса.
117. Индекс цен Ласпейреса равен 1,35; индекс цен Пааше - 1,42. Индекс цен Фишера (с точностью до 0,1%) равен:
а) 140,1; б) 138,5; в) 105,2; г) 97,5.
118. Средний гармонический индекс цен имеет вид:
а)  б)
б)  в)
в) 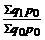 ; г)
; г) 
119. Средний арифметический индекс физического объема товарооборота имеет вид:
а)  б)
б)  в)
в) 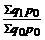 ; г)
; г) 
120. Недостающим элементом в формуле среднего арифметического индекса физического объема товарооборота  является:
является:
а)  б)
б)  в)
в) 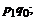 г)
г) 
121. Агрегатный индекс физического объема при исчислении по одним и тем же данным будет… среднему(го) арифметическому(го) индексу(а) физического объема:
а) меньше; б) меньше или равен; в) больше; г) равен.
122. Произведение промежуточных по периодам цепных индексов даст базисный индекс последнего периода, если это индексы:
а) индивидуальные;
б) цен с переменными весами;
в) цен с постоянными весами;
г) физического объема с переменными весами.
123. Имеются следующие данные о динамике объема промышленной продукции по РФ по годам:
| Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| Индексы промышленного производства, % к предыдущему году | 102,0 | 94,8 | 111,0 | 111,9 | 104,9 | 103,7 |
Объем промышленной продукции в 2009 г. по сравнению с 2003 г. составил (с точностью до 0,1%):
а) 142,2; б) 123,4; в) 130,7; г) 99,8.
124. Влияние изменения цен на величину стоимости продаж можно определить по формуле:
а)  в)
в) 
б)  г)
г) 
125.Количество реализованной продукции за текущий период увеличилось на 15%, цены на продукцию за этот период также увеличились на 15%. Стоимость реализованной продукции:
а) увеличилась на 32,3%; в) увеличилась на 5%;
б) уменьшилась на 32,3%; г) не изменилась.
126. Если за изучаемый период времени объем товарооборота в текущих ценах увеличился на 17%, а цены возросли на 12%, то индекс количества продаж товара равен (с точностью до 0,1%):
а) 131,0; б) 104,5; в) 141,7; г) 95,7.
127. Формула индекса цен переменного состава:
а)  в)
в) 
б)  г)
г) 
128. Формула индекса постоянного состава:
а)  в)
в) 
б)  г)
г) 
129. Формула для расчета индекса цен структурных сдвигов:
а)  в)
в) 
б)  г)
г) 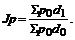
130. Известно, что индекс постоянного состава равен 102,5%, а индекс структурных сдвигов - 100,6%. Индекс переменного состава равен (с точностью до 0,1%):
а) 101,9; б) 98,1; в) 103,1; г) 105,8.
 |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Ганченко О.И. Практикум по общей теории статистики / О.И. Ганченко, М.Р. Ефимова, Е.В. Петрова. - М.: Финансы и статистика, 2008.
2. Дуброва Т.А. Статистика: учебник / Т.А. Дуброва, В.Г. Минашкин, В.С. Мхитарян. - 6-е изд., стер. - М.: Academia, 2007.
3. Елисеева И.И. Общая теория статистики: учебник / И.И. Елисеева, М.М. Юзбашев. - 5-е изд., перераб. и доп. - М.: Финансы и статистика, 2008.
4. Елисеева И.И. Практикум по общей теории статистики: учеб. пособие / И.И. Елисеев, М.М. Юзбашев, Н.А. Флуд. - М.: Финансы и статистика, 2008.
5. Ефимова М.Р. Общая теория статистики: учебник / М.Р. Ефимова, Е.В. Петрова, В.Н. Румянцева. - 2-е изд., испр. и доп. - М.: Инфра-М, 2008.
6. Минашкин В.Г. Практикум по общей теории статистики: учеб. пособие / В.Г. Минашкин, Н.А. Садовникова, Р.А. Шмойлова. - М.: Финансы и статистика, 2008.
7. Минашкин В.Г. Теория статистики: учебник / В.Г. Минашкин и др. - 5-е изд. - М.: Финансы и статистика, 2008.
8. Мхитарян В.С. Практикум по общей теории статистики: учеб.-метод. пособие / В.С. Мхитарян, М.Г. Назаров, Е.И. Ларионова. - М.: КноРус, 2008.
9. Салин В.Н. Статистика: учеб. пособие / В.Н. Салин, Э.Ю. Чурилов, Е.П. Шпаковская. - 2-е изд. - М.: КноРус, 2008.
Учебное издание
Леонтьева Тамара Ильинична
Баканач Ольга Вячеславовна
Дата добавления: 2018-02-15; просмотров: 5264; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
