Задачи статистического изучения явлений во времени

ТЕМА 1.5. ПОКАЗАТЕЛИ ВАРИАЦИИ

1.5.1. Понятие вариации.

1.5.2. Показатели вариации.

1.5.3. Правило сложения дисперсии.

Понятие вариации

Вариация— это наличие различий у отдельных единиц совокупности по какому-либо признаку.

Эта категория занимает особое место в статистической науке, ибо именно наличие вариации единиц совокупности предопределяет необходимость статистики. Если бы отдельные единицы совокупности имели они и те же значения признаков (например, рост, возраст у всех живущих людей был бы одинаковый), то для изучения данной совокупности по этим признакам достаточно было бы изучить только одну единицу совокупности. Однако зачастую значения признаков колеблются, изменяются при переходе от одной единицы к другой. Как правило, вариация является порождением следующих причин:

— своеобразие условий, в которых происходит развитие отдельных единиц совокупности;

— неравномерность развития отдельных единиц.

Например, причиной вариации роста у отдельно взятых людей является генетическая особенность каждого организма (основная причина), особенности питания, экологическая обстановка и т.д.; вариация урожайности может быть вызвана климатическими, почвенными особенностями зоны произрастания, режима и возможности полива, качеством посадочного материала и т.д.

Вариация существует во времени и в пространстве.

Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям (урожайность пшеницы в разных регионах).

Под вариацией во времени подразумевается объективное изменение значений признака в разные периоды (или моменты). Например, со временем изменяется средняя продолжительность предстоящей жизни, доходность предприятий отрасли, уровень потребностей людей и т.д.

Изучение вариации имеет важное значение, так как вариация характеризует степень однородности совокупности. Однородность совокупности — необходимое условие при расчете большинства статистических показателей, в частности средних величин.

Показатели вариации

Показатели вариации являются необходимым дополнением при расчете средних величин, так как определяют степень однородности совокупности.

Система показателей вариациивключает следующее:

— размах вариации;

— среднее абсолютное (линейное) отклонение;

— среднее квадратическое отклонение;

— дисперсия;

— коэффициент вариации.

Значение показателей вариации:

— характеризуются размеры вариации признака;

— показатели вариации дополняют систему средних величин, в которой затушевываются индивидуальные различия;

— показатели вариации позволяют охарактеризовать уровень однородности совокупности;

— с помощью показателей вариации, путем сравнения вариации у отдельных признаков (разных), есть возможность измерить взаимосвязь между этими признаками.

Первый показатель, так называемый размах вариации,— наиболее простой из показателей, характеризует абсолютные размеры изменения признака и определяется как разница максимального и минимального значений признака:

Несмотря на простоту расчета, этот показатель имеет важный недостаток — учитывает только два приграничных значения. В случае аномальности одного или двух приграничных значений, он может исказить действительную вариацию совокупности.

Для того чтобы избавиться от этого недостатка, рассчитывают отклонение каждой индивидуальной величины от средней по совокупности. Таким образом, учитывается значение каждой единицы совокупности. Для того чтобы охарактеризовать это отклонение одним числом, рассчитывают среднюю из этих значений. Данный показатель носит название среднее абсолютное (линейное) отклонениеи определяется следующим образом:

- простой вид;

- взвешенный вид (для сгруппированных данных);

где d(L) — среднее абсолютное (линейное) отклонение;

х — индивидуальное значение признака (варианта);

— среднее из значений признака;

п — численность совокупности;

f — частота.

Среднее линейное отклонениехарактеризует средний размер отклонений индивидуальных значений признака от средней величины. Таким образом, он характеризует абсолютные размеры вариации, имеет те же единицы измерения, что и признак, вариацию которого характеризует.

Недостаток: ввиду того, что применяется модуль, затруднено проведение математических операций. Поэтому он применяется редко.

Для того чтобы избавиться от недостатка предыдущего показателя, разницу между индивидуальным значением и средней возведем в квадрат и затем извлечем корень квадратный из полученного среднего значения. Полученный показатель будет называться среднее квадратическое отклонение:

- простая.

- взвешенная.

Играет ту же роль, что и среднее абсолютное отклонение, но, имеет перед ним одно преимущество, а именно, с ним проще проводить математические операции. Ввиду этого в 90 случаях из 100 используется этот показатель.

Еще более удобный для математических преобразований показатель вариации — дисперсия,который представляет собой среднее квадратическое отклонение в квадрате:

- простая,

- взвешенная.

С помощью дисперсии и среднего квадратического отклонения измеряются взаимосвязи между различными признаками. Кроме того, по этим показателям можно сравнивать совокупности в смысле их однородности по одинаковым признакам.

Вывод об однородности совокупности позволяет сделать коэффициент вариации, который может быть рассчитан несколькими способами в зависимости от исходной информации:

- характеризует средний процент отклонений индивидуальных значений признака от средней величины.

где V – коэффициент вариации;

σ – среднее квадратическое отклонение;

d (L) – среднее линейное отклонение;

Х_МО – мода (структурная средняя);

Х_МЕ – медиана (структурная средняя).

Коэффициент вариации имеет большое значение. Он позволяет сравнивать уровень вариации по различным признакам и используется для характеристики однородности совокупности. Если коэффициент вариации меньше 33%, то совокупность однородна.

Пример расчета показателей вариации.

Распределение студентов вуза по возрасту характеризуются следующими данными (табл. 1):

Таблица 1

Возраст студентов, лет	Число студентов очно-заочного отделения, чел.	Число студентов дневной формы обучения, чел.	Х_i,лет
17—20	5	60	12,5
20—23	36	120	21,5
23—25	48	90	24,0
25—28	52	55	26,5
28—30	80	10	29,0
30 и старше	99	3	31,0

Рассчитайте показатели, характеризующие вариацию возраста студентов для каждой формы

обучения. Сравните полученные результаты.

Рассчитаем показатели вариации, характеризующие совокупность студентов очно-заочной формы

обучения.

1. Размах вариации:

R = x_max – x_min = 31 - 18,5 = 12,5 (лет)

2. Средняя арифметическая:

3. Среднее линейное отклонение:

Возраст отдельно взятого студента отклоняется от среднего по совокупности возраста — 27 лет — на 3 года. То есть можно утверждать, что возраст наибольшего числа студентов не будет выходить за границы интервала: от 24,3 до 30,4 лет.

27,36 - 3,07 < 27,36 < 27,36+ 3,07.

Среднее квадратическое отклонение:

Среднее квадратическое отклонение также характеризует абсолютную величину отклонения индивидуального значения от средней. Как правило, значение среднего квадратического отклонения больше среднего линейного отклонения.

Дисперсия:

=13,899

Характеризует квадрат отклонений индивидуального значения от средней величины. Коэффициент вариации:

Средний процент отклонений индивидуальных значений от средней величины составляет 13,6%. Совокупность однородна. Сделаем аналогичные расчеты по совокупности студентов дневного отделения. Получаем следующие результаты:

R = 12,5

= 21,69

d(L) = 3,40

σ = = 4,74

σ²=22,54

V = 21,9%

На основании приведенных расчетов можно сделать вывод о том, что совокупность студентов очно-заочного отделения более однородная.

Расчет показателей вариации — достаточно трудоемкий процесс. В некоторых случаях, когда имеется ряд показателей с равноотстоящими моментами времени или равноинтервальный ряд распределения, расчет может быть упрощен. Сокращенные способы расчета дисперсии базируются на знании свойств дисперсии. Свойства дисперсии:

— если от всех значений варианты х отнять (прибавить) постоянное число А, то дисперсия не изменится;

— если каждое значение варианты разделить (умножить) на постоянную величину к, то дисперсия уменьшится (увеличится) в к² раз.

Сокращенные способы расчета дисперсии:

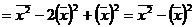
2. Способ моментов – применяется только в случае равенства интервалов.

, где i – величина интервала;

- момент 2-го порядка, , где х′ - момент 1-го порядка.

Пример.

Имеются следующие данные о распределении семей по уровню среднедушевого дохода (табл. 2).

Таблица 2

Средний душевой доход, руб.	Число семей в группе	х,	х'	x'f	x'²f
До 200	10	150	-4	-40	160
200—300	35	250	-3	-105	315
300-400	68	350	-2	-136	272
400—500	70	450	-1	-70	70
500—600	75	550	0	0	0
700—800	30	650	1	30	30
800 и более	12	750	2	24	48
Итого	300			-297	895

Как правило, в качестве константы А выбирается варианта с наибольшей частотой (для максимального упрощения расчетов). Наибольшая частота равна 75, значит А = 550.

На основании приведенных расчетов можно сделать вывод о том, что совокупность семей однородна. Однако коэффициент вариации приближается к верхней границе (33%), превышение которой свидетельствует о неоднородности совокупности. То есть в данной совокупности достаточно высокий уровень вариации. Средний душевой доход по всей совокупности семей составляет 451руб., а среднее отклонение от этого уровня — 141 руб. Поэтому можно констатировать достаточно высокую разницу между уровнем дохода отдельно взятых семей и, как следствие этого — начавшийся процесс расслоения общества. Дополнительные выводы можно сделать, рассчитав структурные средние — моду и медиану.

Правило сложения дисперсии

Если данные представлены в виде аналитической группировки, в статистике рассматривают три вида дисперсии:

— общая дисперсия;

— дисперсия средняя из внутригрупповых;

— межгрупповая дисперсия.

Общая дисперсияизмеряет вариацию признака х во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию.

Межгрупповая дисперсия(факторная) объясняет вариацию, вызванную признаком, положенным в основу группировки. Средняя из внутригрупповых дисперсия(остаточная) объясняет ту часть вариации, которая вызвана действием (влиянием) на признак х всех остальных признаков (факторов), кроме группировочного.

Правило сложения дисперсиизаключается в том, что общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий:

где - межгрупповая дисперсия;

- средняя из внутригрупповых дисперсия.

Расчет средней из внутригрупповых проводится в два этапа. Первоначально рассчитываются дисперсии по каждой группе, как квадрат отклонений индивидуальных значений признака в группе от средней, рассчитанной в пределах группы:

, ,

где п_i — численность i-ой группы.

На втором этапе по средней арифметической взвешенной рассчитывается средняя из внутригрупповых дисперсия:

Межгрупповая дисперсия определяется как квадрат отклонений средних, рассчитанных по каждой группе от средней, рассчитанной в пределах всей совокупности, взвешенных численностью группы:

Правильность расчетов дисперсии при помощи правила сложения дисперсии можно подтвердить расчетом общей дисперсии по обычной формуле.

Поскольку правило сложения дисперсии позволяет разложить дисперсию на дисперсию, возникающую под влиянием факторного признака (группировочного), и остаточную дисперсию, оно широко используется при изучении взаимосвязей между признаками.

На основе правила сложения дисперсии в статистике разработаны меры связей между факторным и результативным признаками: коэффициент детерминации и эмпирическое корреляционное отношение.

Коэффициент детерминацииопределяется как отношение межгрупповой дисперсии к общей дисперсии:

Коэффициент детерминации характеризует долю общей колеблемости результативного признака, которая вызвана признаком, положенным в основу группировки.

Эмпирическое корреляционное отношениехарактеризует тесноту связи между признаками и определяется следующим образом:

Пример использования правила сложения дисперсии.

Имеются данные о распределении магазинов по объему товарооборота (табл. 3):

Таблица 3

Товарооборот, тыс. руб.	Число магазинов в группе	Издержки обращения, тыс. руб.
1000—1200	3	20,30,40
1200—1500	5	45, 60, 90, 40, 80
1500—2500	4	80,85,98,100

Определите общую дисперсию, используя правило сложения дисперсии.

= 527,9 + 197,3 = 725,13

Для проверки правильности расчетов определим общую дисперсию обычным способом:

Это значит, что 72,8% вариации издержек обращения объясняется признаком, положенным в основу группировки, то есть товарооборотом. Соответственно, 27,2% вариации результативного признака может быть объяснено прочими факторами, не учтенными в группировке:

Эмпирическое корреляционное отношение — показатель тесноты связи. Он характеризует уровень согласованности в изменениях факторного признака» (объем товарооборота) и результативного признака (величина издержек обращения).

Эмпирическое корреляционное отношение показывает степень влияния товарооборота на издержки обращения. Иногда дают вероятностную интерпретацию: с вероятностью 0,853 мы можем предсказать изменения издержек обращения, зная изменение товарооборота.

Значения эмпирического корреляционного отношения лежат в диапазоне от 0 до 1: О - 0,3 — слабая связь;

0,3 - 0,7 — умеренная;

0,7 - 1,0 — сильная.

Выводы:

1. Наличие вариации обусловливает необходимость статистики. Статистика изучает только варьирующие явления.

2. Показатели вариации характеризуют однородность совокупности и служат необходимым дополнением при расчете средней величины.

3. Для упрощения расчетов основного показателя вариации — дисперсии — применяют сокращенные способы расчета дисперсии, основанные на свойствах дисперсии.

4. На основании дисперсии (правило сложения дисперсии) рассчитывается эмпирическое корреляционное отношение и коэффициент детерминации, которые служат для характеристики взаимосвязи между признаками.

Библиографический список

основной

1. Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И.И.Елисеевой.— М: Финансы статистика, 2000.— С. 74—117.

2. Практикум по теории статистики: Учеб. пособие / Под ред. проф. Р.А. Шмойловой.— М: Финансы и статистика, 1999.— С. 122—129.

3. Статистика: Курс лекций / Под ред. В.Г. Ионина.— Новосибирск: Издательство НГАЭиУ, 1996.— С. 59—84.

4. Теория статистики: Учебник / Под ред. проф. Р.А. Шмойловой.— М., 1996.

дополнительный

1. Лунеев В.В. Юридическая статистика: Учебник.— М.: Юристь, 1999.— С. 272—276.

2. Савюк Л.К. Правовая статистика: Учебник.— М.: Юристь, 1999.— С. 412—416.

ТЕМА 1.6. РЯДЫ ДИНАМИКИ

1.6.1. Задачи статистического изучения явлений во времени.

1.6.2. Ряды динамики, их классификация.

1.6.3. Правила построения рядов динамики.

1.6.4. Показатели анализа рядов динамики.

1.6.5. Способы выравнивания динамических рядов. Экстраполяция и интерполяция.

Задачи статистического изучения явлений во времени

Для полной статистической характеристики явления или процесса необходимо рассмотреть изменение его характеристик во времени, то есть в динамике, с целью выяснения закономерностей развития данного явления, процесса. В ходе изучения динамики любого явления должны быть решены следующие задачи:

— характеристика интенсивности изменений во времени статистических показателей (от периода к периоду);

— определение средних показателей во времени;

— выявление закономерностей изменения явлений во времени;

— экстраполяция, интерполяция;

— анализ факторов, определяющих изменения показателей во времени.

Эти задачи решаются с помощью построения и анализа динамических рядов.

Дата добавления: 2018-02-15; просмотров: 668; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 Следующая ⇒

Мы поможем в написании ваших работ!